基于灾害链理论与FAHP的灾害风险评估研究

李云飞，许令顺，张 飞，杨 静，汪炜昊，胡浩然

(1.清华大学合肥公共安全研究院科学研究部，安徽 合肥 230601；2.安徽省城建设计研究总院股份有限公司技术中心，安徽 合肥 230051；3.合肥市城市生命线工程安全运行监测中心交通安全部，安徽 合肥 230601)

灾害风险评估可以有效预防、降低灾害系统性风险，有助于人们应对更加多样化的灾害风险类型。世界各国有关政府部门已经把灾害风险评估作为重点关注问题，相关领域的研究也受到越来越多国内外研究机构和学者的关注，并展开了一系列的研究，取得了很大的进展[1]。

基于灾害之间耦合相关性，将单一灾害风险概率结果进行综合叠加计算，是实现灾害风险评估的经典方法[2-3]。而学者Menoni S提出用灾害损失破坏链的概念替代简单的灾害耦合关联损失观念[4]，Burkholder等人也提出实际灾害受自然物理系统内部作用，并与人类社会相互影响，认为不存在纯粹的单一灾害，进一步指出不断的演化扩散是现实灾害具有的重要特征[5]。随着针对灾害链式规律进行不断深入的探讨，以及针对不同类型链式特征构建理论模型，从而形成了较为系统的灾变链式理论及应用体系[6-7]。近些年，灾变链式理论在灾害风险评估方面应用较多，包括特大地震灾害链风险评估[8]、基于灾害链城市多灾种综合防灾预警[9]以及区域灾害链风险评估等[10]。上述这些研究进一步丰富了灾变链式理论和应用，但这些评估主要倾向于定性研究。

在灾害风险定量评估方面，模糊层次分析法已成为有效的评估方法[11]。Yan等根据道路塌陷灾害的形成机理和主要影响因素，采用多层次模糊综合评价法，建立了道路塌陷危险性评价模型[12]。孙艳丽等采用层次分析法，结合TOPSIS法提出了煤矿突发事件应急能力的评价模型[13]。另外，模糊层次分析法也在特定区域地震风险评估[14]，危险化学品风险评估[15]，特定区域水质风险评估[16]等方面有很好的应用。然而，层次分析法在各层级指标权重选取上更多依赖专家人工的主观评分，多个专家的评分可能存在较大差异，对后续的相关风险评估带来困扰。

基于以上分析，本文采用灾害链理论和模糊层次分析法相结合的方法，基于事件链和统计概率的灾害链模型可以针对灾害链各层级的灾害因素进行定量分析，从而尽量避免层次分析法中权重选取的主观性，以此进行灾害环境下安全风险评估技术的研究，为灾害风险评估提供一种思路和技术手段，也为相关研究提供参考借鉴。

1 基本原理

从灾害中的致灾因子与情景分析为出发点，对灾害事件作用进行解析，基于灾害事件链理论，形成事件表和灾害传递链条，根据灾害链中相关事件的因果关系确定灾害因素层次划分，结合事件概率和模糊层次分析，得到各层灾害因素权重和模糊综合评价矩阵，进而计算得到灾害风险评估等级。基本原理如图1所示。

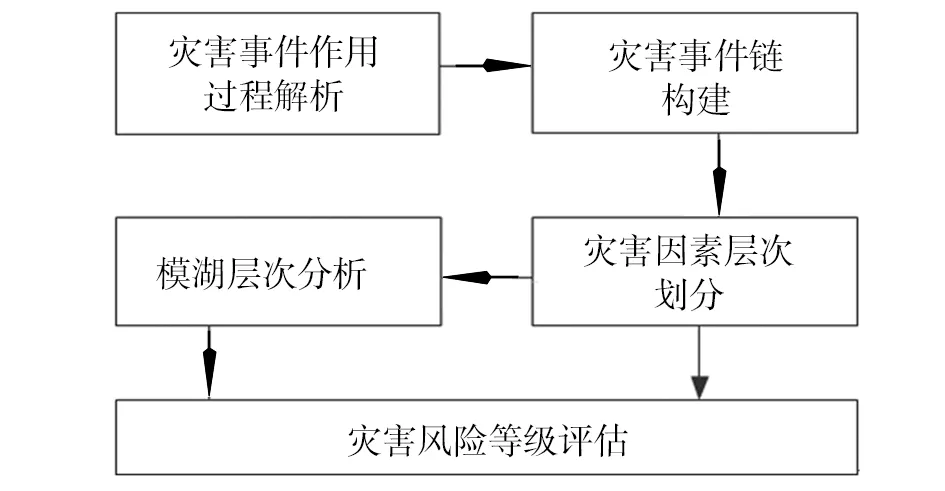
图1 基本原理框图

2 灾害事件链构建

2.1 灾害事件作用过程解析

根据灾害链理论，突发事件的发生发展以及衍生次生事件链的产生是多种自然物理因素与人类社会因素相互作用的结果。同时，现有灾害理论认为灾害是地球表层孕灾环境、致灾因子和承灾体三者之间相互作用的综合产物。因此，灾害事件的发生、发展和演变具有显著的时域特征，该过程取决于事件的内在作用机理。从承灾体的完好度、事件的作用强度和承灾体的恢复力三个方面，在承灾体对不同作用形式响应特性的基础上，建立起相关事件作用过程的分析模型，如图2所示。

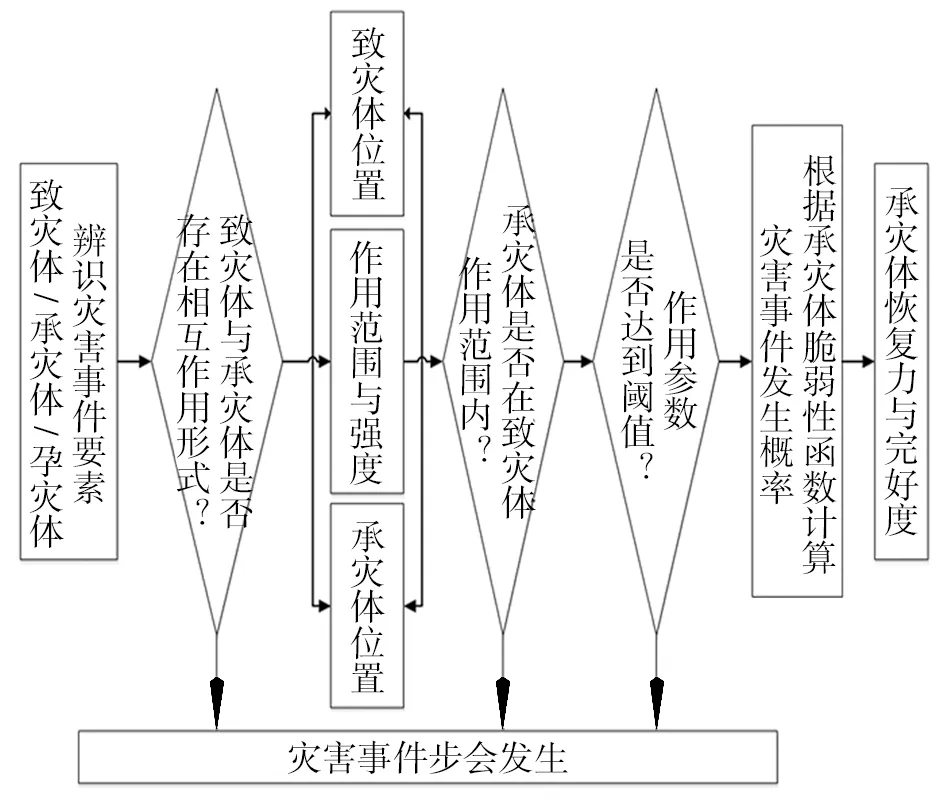
图2 灾害事件作用过程的分析模型

上述模型通过针对灾害事件作用过程的建模，充分考虑到各类事件的共性特征，提供了一种统一的分析技术。基于技术能够体现各类灾害场景中承灾体的响应特性，从而将作为本项目中进行灾害机理分析和推演的重要基础。

世界中的各种客观事物都是可细分的，所以非常规突发事件中的致灾因子、承灾体与孕灾环境也是可分的。对于承灾体，由于事件发生时人们的关注点不同，承灾体的选择会有所不同。例如，当地震事件发生时，将城市作为承灾体；当关注于城市内的破坏情况时，将各工厂、学校、社区分别作为承灾体；当关注于石油化工厂受到的破坏情况时，将储罐、管道、生产设施分别作为承灾体；当关注地震后传染病的流行情况时，将人群作为承灾体。由此可以看出，承灾体具有可分性、层次性的特点。

根据系统工程的特点，可将承灾体看作一个系统，系统具有可分解性。即任意承灾体皆可分解为不同的子承灾体，子承灾体又可继续分解为不同的次一级子承灾体，如此可进行多级分解，直到组成承灾体的最小单元为止。

2.2 灾害事件链

灾害事件，尤其是严重事件，其在发生过程中往往诱发多个或多级次生衍生事件，因而普遍具有链式效应规律。基于前述分析框架对事件对象的转化特征进行了分析，建立起灾害链结构分析和演化推理框架。

重大灾害场景由存在偶合、次生、衍生和异变等关系的灾害事件组成，各事件在作用形式的驱动下进化演变形成灾害链。相关场景、事件均基于致灾体、承灾体、孕灾体和作用形式四个要素进行分析，同时展示出灾害链的演化机理，构成开展灾害情景推演的基础。

以上对灾害链模型进行了描述与定性的分析。下面通过概率分析方法对灾害事件链中各灾害要素间的依赖关系进行分析，特别是对致灾因素之间传递关系进行解析，进而对灾害链模型进行定量分析与构建[17]。首先，将灾害链模型中经作用过程解析后的各个灾害要素所对应关系节点进行编码，用pdij表示；其次，将灾害链模型中各个灾害要素及各节点间的作用关系用plij表示；最后，根据灾害链模型中致灾环、激发环和损害环三者之间的层次关系，得到编码后的灾害链模型如图3所示。

图3 概率编码灾害链

从概率分析理论角度来看，图3中所示编码pdij表示灾害链中各灾害要素所对应的事件节点所发生的概率，plij编码表示灾害链中各灾害要素所对应事件节点之间联系关系的条件概率，从而可得到灾害链中每层灾害要素及关系节点发生概率的计算公式为

pd(i+1,j)=1-∏(1-pd(i,j)×pl(i,j))

(1)

式中：pd(i+1,j)为灾害链中当前层次各灾害要素所对应事件节点发生的概率；pd(i,j)为与该灾害要素所对应事件节点相关联的上一层次灾害要素所对应事件节点发生的概率；pl(i,j)为上一层次各灾害要素事件节点发生情况下当前层次灾害要素事件节点发生的条件概率。

3 模糊层次分析

3.1 灾害风险层次划分与权重分配

针对上述灾害事件链中每个灾害要素事件节点，按照其所在灾害链中的层次进行划分。把灾害链中所有灾害因素节点整理成如下集合

U={u1,u2,u3,…,un}

其中：n为灾害链中所有灾害因素节点的个数，由具体的评估需求和场景决定。

根据灾害链中灾害因素节点所在层次，把灾害因素分为多个层次。

每层灾害因素集为：Ui={ui1,ui2,…,uij}

其中：1≤i≤m，m为总层数，j为每层灾害因素集元素个数。

根据每个灾害因素节点的发生概率大小，应用层次分析法来确定各层次因素集的权重分配集。通过比较灾害因素节点发生概率，确定指标间的两两重要程度，采用1～9标度法得到各层次因素集的权重矩阵Ai(i=1，2，...，q)，其中q为各层次灾害因素集总数目。

3.2 评价集确定和模糊评判矩阵构建

评价集是对灾害链中各层次灾害因素评价指标的一种定性化表式。在实际操作中，其是根据灾害区域实际情况和专家意见对各层次灾害因素指标所给出的评价的集合。记为

V={v1,v2,v3,…,vp}

模糊综合评价是一种十分有效的多因素综合决策方法，其特征是评价结果不是绝对的肯定或否定，而是以一个模糊集合来表示，从而可以对多种因素影响的事件做出全面综合评价。模糊评判矩阵是模糊综合评价方法的核心概念，其本质是灾害因素集U到风险评价集V的一个模糊映射。在进行模糊综合评价之前需要确定模糊评判矩阵，通常可以采用单因素模糊评价、隶属度函数等方法进行确定。其中隶属度函数属于模糊评价函数中的概念，隶属度取值区间为[0,1]，当某个隶属度rij取值越接近于1，表示灾害因素ui对评价等级vj的隶属程度越高。以灾害链中第i层级为例，假设此层级灾害因素集元素个数为j，请若干专家对各灾害因素分别就上述评价集中的p个评价指标通过投票进行评价，即可得到评价矩阵Ri，记为

3.3 模糊综合评判

根据模糊层次分析法计算流程，应用线性加权平均模糊综合评判模型求出最低层次所有灾害因素集的综合评价向量Bim，计算方法如下

Bim=wim·Rim

(2)

其中：1≤i≤q，q为最低层次灾害因素集个数，wim为最低层次第i个灾害因素集的权重矩阵Aim的最大特征向量，Rim为上述模糊综合评价矩阵。

在此基础上得到上一层次的灾害因素集的模糊评价矩阵Bm-1=(B1m,B2m,…,Bqm)T，结合上一层次灾害因素集权重矩阵Am-1的最大特征向量wm-1求得再上一个层级模糊评价矩阵Bm-2，按照此计算流程通过不断迭代计算，最后得到最高层次灾害因素评价向量B={b1,b2,…,bp}，也就是模糊综合评价向量，其中最大元素值bj所对应评价集中第j个评价指标vj即是最终的灾害风险评估等级。

4 实例分析

4.1 灾害链构建

地震作为破坏性较大的自然灾害，其会引发一系列次生、衍生事件，如滑坡、建筑物坍塌、危化品泄漏、地面塌陷、管网破损等。所以，地震作用于承灾体属于一对多复杂事件。当承灾体为地下管网、发电厂与道路设施时，可能会引地下管网受损、电力中断和交通瘫痪等次生衍生事件。根据灾害链理论模型，得出用于本文讨论的具有三层等级地震灾害链，如图4所示。本文以此为例来说明与验证前面提出的计算模型，对于地震引发的其他事件以及更深层次灾害链也适用于本文上述计算方法，这里不进行分析与探讨。

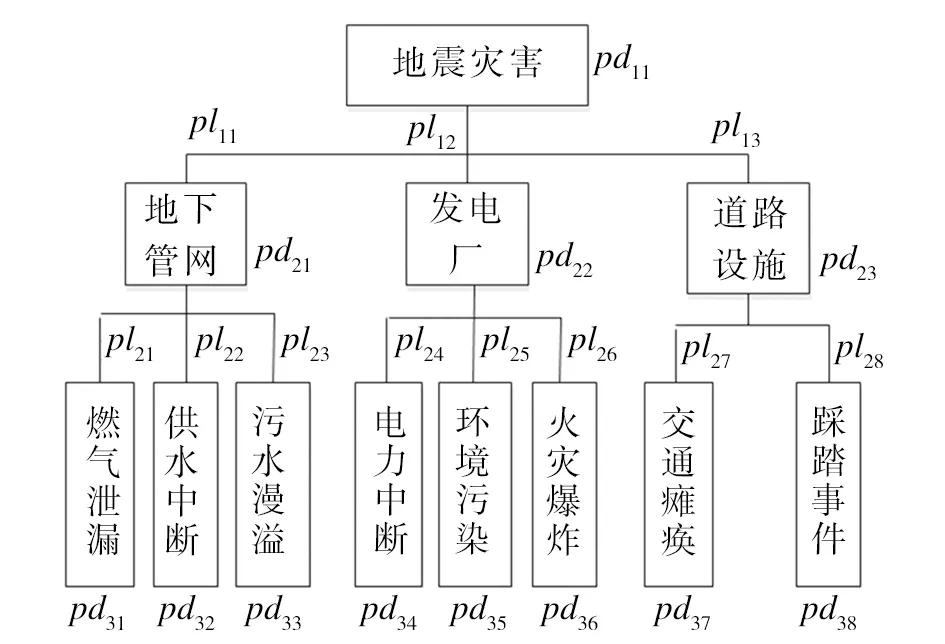
图4 三层级地震灾害链

在对危险性进行评估时，釆用6级以上地震次数占总地震次数的百分比来表示某一地区的地震危险性。根据文献[18]中的数据，以江西省为例，6级以上地震发生为10%，即认为发生地震概率pd11为0.1，同时评估灾害链中每条灾害传递概率，如表1所示。根据灾害链计算模型，可计算得到每层次灾害因素节点概率，如表2所示。

表1 灾害传递概率

表2 灾害因素节点概率

4.2 灾害风险因素集权重矩阵

由pd21、pd22和pd23进行两两比较分析，根据数值比例关系确定因素间重要关系，根据采用1～9标度法得到地震灾害一级风险因素集的权重矩阵A11如下所示。

计算可得A11最大特征值和特征向量为λ11=3.03，w11={0.50, 0.15, 0.85}。

同理，由pd31、pd32和pd33得到地下管网地震灾害风险因素集的权重矩阵A21，由pd34、pd35和pd36得到发电厂地震灾害因素集权重矩阵A22，由pd37和pd38得到路设施地震灾害风险因素集权重矩阵和A23。

计算A21、A22和A23最大特征值和特征向量分别为

λ21=3.14，w21={0.27, 0.56, 0.78}，

λ22=3.0，w22={0.96, 0.19, 0.19}，

λ23=2.0，w23={0.994, 0.11}。

4.3 模糊综合评价

本例中对地震灾害风险等级划分为四个等级，即V={低，较低，中，高}。

本例侧重对本文灾害风险评价计算模型进行重点说明和讨论，为了简化问题，在单因素模糊评价矩阵方面，依据当地现场情况和专家经验，采用定性评价方式对单因素模糊评价矩阵进行确定，得到地下管网、发电厂和道路设施等地震灾害因素集的风险等级模糊评价矩阵。

由w21与R21各列进行点积计算可得地下管网地震灾害风险等级模糊评价向量B21，如下所示。

B21=w21·R21= {0.19, 0.49, 0.61, 0.31}

同理，可得B22={0.29, 0.31, 0.63, 0.12}，B23={0.45, 0.42, 0.12, 0.11}。

由向量B21、B22和B23组成地震灾害风险综合模糊评价矩阵B11，由w11与B11各列作点积运算可得地震灾害风险综合评价向量B={0.52, 0.65, 0.50, 0.27}。向量B中最大元素值为0.65，其所对应的地震灾害风险等级为“较低”。

5 结论

在承灾体对不同作用形式响应特性的基础上，建立起相关事件作用过程的所形成的灾害链。通过概率分析方法对灾害链中各灾害要素间的关系进行定量分析。针对灾害事件链中每个灾害要素节点，按照其所在灾害链中的层次进行划分。根据灾害因素节点的概率数值比例关系确定因素间重要关系，构建各层次因素集的权重矩阵，结合模糊层次分析法，可计算得到灾害风险综合评价向量，进而得出最终的灾害风险评估等级。以地震灾害为例，针对地下管网、发电厂与道路设施等承灾体，构建具有三层等级地震灾害链，并以此为例来说明与验证本文提出的灾害风险评估模型。