KNOT认证加密算法的零和区分器分析

叶 涛，韦永壮，李灵琛

(1.桂林电子科技大学 信息与通信学院，广西壮族自治区 桂林 541004；2.桂林电子科技大学 广西密码学与信息安全重点实验室，广西壮族自治区 桂林 541004；3.密码科学技术国家重点实验室，北京 100878)

伴随着物联网技术和5G通信技术的快速发展，各种移动通信终端以及物联网中的传感器终端遍布于人们的实际生活。如何确保通信的安全变得愈加重要。轻量级密码算法作为一种重要的加密体制，具有易于实现、加解密速度快、占用资源少等优势，非常适用于这些资源受限的环境中，所以，轻量级密码算法的设计[1]与分析[2]是近些年的研究热点。最近，NIST(美国国家标准与技术研究院)发起了轻量级密码算法征集竞赛[3]活动，旨在面向全世界公开征集适用于资源受限环境下的轻量级密码算法，其中第1轮共有56个候选算法。经过第1轮的安全性评估，现有32个密码算法入围第2轮，KNOT密码算法[4]是其中之一。KNOT密码算法是由ZHANG等人设计的，由于其可以充分地利用比特切片法来实现，所以该算法具有优秀的软件和硬件实现性能。KNOT具有认证加密功能和哈希运算的功能，这些性能的好坏依赖于KNOT内部轮置换函数的安全性。KNOT置换有3个版本，按照每个置换的分组长度，标记为KNOT-256，KNOT-384和KNOT-512，其中KNOT-256算法的软硬件实现所占用的资源最少，非常适用于资源受限的环境中。在KNOT的设计文档中，算法的设计者认为KNOT-256至少需要49轮才能抵抗差分分析和线性密码分析，同时认为KNOT-256算法存在的最长不可能差分区分器的轮数为17轮。对于积分分析，算法的设计者给出了17轮的积分区分器，需要的数据复杂度为2255。但是，是否存在更高轮的区分器还需要进一步研究。因此，如何给出KNOT认证加密算法安全性新评价是目前的研究热点。

2009年，AUMASSON和MEIER等首次提出零和区分器[5]的概念，本质上这个区分器可以看做扩展的积分区分器[6]。由于零和区分器一般是在已知密钥[7]的前提下构造的，所以构造零和区分器的一般方法是从中间状态向加密方向和解密方向构建积分区分器，并将这两个积分区分器连接到一起[8]。此外，也可以通过利用迭代置换的特殊性质[9-10]来构建零和区分器。但是，这些方法是基于算法结构或者算法本身具有的特殊性质提出的，不具有通用性。可分性[11]的提出在很大程度上解决了这个问题。可分性是广义的积分性质，利用优化工具求解可分性的混合整数线性规划模型(MILP)，攻击者可以构建出高轮的积分区分器。近些年来，利用可分性质结合自动化搜索工具来构建零和区分器成为了密码学者的研究热点内容之一[12-13]。可分性的标志位技术[14]是在2018年的美密会上由WANG等人提出的，相比于传统的可分性分析方法，利用添加标志位的可分性技术可以提高可分性的MILP模型的精确性和扩展区分器的轮数，同时能够提高搜索区分器的效率。将标志位技术应用于分组密码算法零和区分器的搜索中能否提高零和区分器的轮数或缩减需要的计算复杂度，还需要进一步研究。

笔者首先给出了密码S盒可分性模型的新构建方法；结合KNOT-256算法的结构特点，给出了KNOT-256算法的可分性新模型，并由此设计了KNOT-256密码算法的零和区分器自动化搜索方法。研究结果表明：KNOT-256存在20到30轮的零和区分器，这里仅提供第20轮和第30轮的结果，详见表1。

表1 KNOT-256分析结果

文中用到的符号定义见表2。

表2 符号说明

1 基础知识

1.1 可分性质以及积分区分器的构造

可分性[11]最初是由TODO在2015年提出的，这是一种广义的积分性质。2016年，TODO等人提出了基于比特的可分性质[15]，其具体的定义如下。

(1)

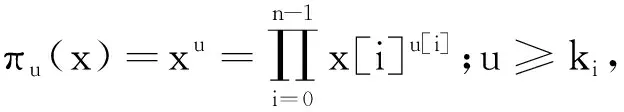
为了更好地描述可分性的传播性质，文献[16]中提出了可分性轨迹的概念，并给出了复制、与、异或等基本运算以及S盒的可分性传播模型。利用这些模型，可以构建出一个不等式系统来描述可分性的传播轨迹，然后利用优化求解工具，如GUROBI[17]，通过判断模型是否有解来确定积分区分器是否存在。

1.2 可分性的标志位技术

在利用可分性质搜索积分区分器时，活跃位置对应的模型变量设置为1，其余的固定位置对应的模型变量设置为0。在实际的密码算法中，如果将这些固定的位置设置为不同的值，可分性的传播轨迹会受到影响。所以，为了更精确地描述可分性的传播性质，WANG等人在2018年的美密会上提出了可分性的标志位技术[14]。

对于可分性的MILP模型中的变量v，定义其对应的标志位为v.F∈{1F，0F，δ}，其中，1F表示变量在算法的内部状态的值为1，0F表示变量在算法的内部状态的值为0，δ表示变量在算法的内部状态的值不确定。标志位的“异或”运算规则为

(2)

标志位的“与”运算规则为

(3)

利用算法的结构，结合标志位的基本运算规则，可以得到密码置换任意的中间状态对应的标志位。在对密码算法的可分性质构建模型时，需要考虑标志位对模型的影响。标志位的影响主要表现在“与”运算的模型上。

(4)

1.3 KNOT-256置换介绍

KNOT密码算法[4]是国际轻量级密码算法标准化征集竞赛活动的第2轮候选算法之一[3]。按照分组长度，KNOT置换分为KNOT-256、KNOT-384和KNOT-512。其中，KNOT-256非常适用于在资源受限的环境下使用，所以笔者重点研究KNOT-256置换的安全性。KNOT-256置换的轮函数包含轮常数异或、列替换、行移位3个基本操作。

首先定义KNOT-256置换的第i轮的输入状态为Wi，输出状态为Wi+1，i≥0。Wi的具体形式如下：

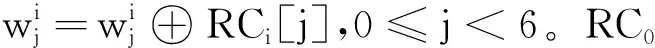
(2) 替换SubCol(Wi)：KNOT-256密码算法的S盒对每一列进行操作，具体的操作方式如下：

表3 KNOT置换的S盒

(3) 行移位ShiftRow(Wi)：KNOT-256行移位操作对中间状态的每行进行操作，其中第0行不移位，第1行循环左移1位，第2行循环左移8位，第3行循环左移25位，得到的状态为第i轮的输出状态Wi+1。

2 新零和区分器构建方法

2.1 零和区分器基本构建方法

零和区分器[5]的概念是由AUMASSON和MEIER在2009年提出的，其基本的定义如下。

可以利用可分性质分别在加密方向和解密方向构建积分区分器，然后将这两个积分区分器连接在一起得到零和区分器。具体的步骤如下：

① 定义加密n1轮后的状态对应的模型变量为vn1，选取活跃变量的下标集合为V，则vn1[j]=1，j∈V，其余固定为常数的位置的模型变量赋值为0，按照可分性的传播模型构建算法解密n1轮的可分性模型，并搜索对应的积分区分器。

② 选取同样的活跃位置V，构建算法加密方向n1+1轮到n1+n2轮的可分性模型，并搜索对应的积分区分器。

③ 如果①和②都存在积分区分器，则可以得到n1+n2轮的零和区分器，构建这样的区分器需要的数据复杂度为2|V|。

2.2 基于可分性和标志位技术的零和区分器搜索方法

对于典型的分组密码算法，其非线性层一般是由多个S盒构成的。如何构建基于标志位的S盒的可分性传播模型，是需要重点研究的问题。下面给出了算法1。

定义n比特S盒的输入x={x0，x1，…，xn-1}，S盒的输出表达式为S(x)，特别地，S(x|I，C)表示输入固定xi0=c0，xi1=c1，…，xi|I|-1=c|I|-1后对应的输出表达式。如果I，C都为空的集合，则S(x)=S(x|I，C)。

算法1添加标志位后S盒的可分性传播轨迹。

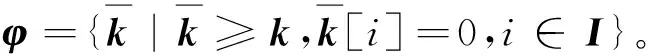
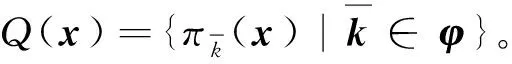
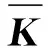
⑤y=S(x|I，C)。

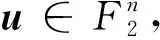
⑧ 返回K。

算法2缩减LS(x|I，C)，得到S(x|I，C)对应的可分性MILP模型MS(x|I，C)。

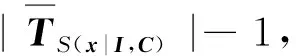
③Ei=[]。

④ 对于j从0 到|LS(x|I，C)| - 1，重复执行⑤到⑦。

⑤ val=lj·(ti‖1)，

⑥ 如果val<0：

⑦ 将j添加到集合Ei中。

⑧ 定义M为空的MILP模型。

益智仁挥发油对东莨菪碱致小鼠学习记忆障碍的改善作用研究 …………………………………………… 马俊俏等（22）：3074

⑨ 定义模型M中的变量z0，z1，…，z|LS(x|I，C)|-1。

算法2的输出表示排除S(x|I，C)全部的不可能可分性轨迹需要的最少的不等式。其中，算法2的第2行到第7行的作用是得到可以删除S(x|I，C)的不可能可分性轨迹ti的不等式的下标集合Ei；第8行到12行的作用是构建用于缩减LS(x|I，C)的MILP模型；第13行到第19行的作用是对模型进行求解。模型如果有解，则判断是否存在zi=1；如果zi=1，则说明li包含在缩减后的不等式系统中；如果模型无解，则说明S(x|I，C)的可分性传播轨迹不构成凸包，需要使用“复制”“与”“异或”运算的模型来构建S(x|I，C)的可分性传播模型。

输入不同的I，C到算法1和算法2中，可以得到不同的标志位对应的S盒的可分性的MILP模型MS(x|I，C)，这些不同的模型预先存储到一个大表中。当构建算法的可分性模型时，首先基于算法结构，按照式(2)和式(3)计算经过每一步操作后的状态对应的标志位。在对S层操作前，先根据标志位判断每一个S盒对应的I和C，然后将对应的模型MS(x|I，C)添加到密码算法轮函数的可分性模型中。对于轮函数中的其余的线性变换，如行移位、轮常数加、轮密钥加等操作，标志位对可分性模型没有影响，这些操作的可分性模型的构建和标志位的转化是独立进行的。这样迭代多轮后，可以分别构建出加密方向和解密方向的可分性模型，然后再利用2.1节中的方法来搜索零和区分器。为了更好地体现可分性的标志位技术以及新的S盒的可分性模型在构建零和区分器中发挥的积极作用，对KNOT-256置换的安全性进行了评估。

3 KNOT-256置换的零和区分攻击

3.1 KNOT-256的S盒可分性的MILP模型构建新方法

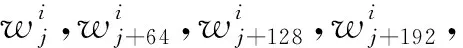
表4 KNOT算法S盒的可分性传播轨迹

将KNOT的S盒的可分性轨迹作为SAGE软件中的函数inequality_generator( )的输入，可以得到201个线性不等式LS(x)；然后利用算法2缩减LS(x)中的不等式，可以得到S盒的可分性传播模型为MS(x)。具体的表达式如下：

(5)

当集合I和C不为空集时，利用算法1和算法2可以得到固定位置I后S盒的可分性模型MS(x|I，C)。以I={2，3}，C={0，0}为例，可以得到此时对应的可分性轨迹TS(x|{2，3}，{0，0})，如表5所示。

表5 S(x|{2，3}，{0，0})的可分性轨迹

将可分性轨迹TS(x|{2，3}，{0，0})输入到SAGE软件中的函数inequality_generator( )中，可以得到11个不等式LS(x|{2，3}，{0，0})。将LS(x|{2，3}，{0，0})输入到算法2中，可以得到S(x|{2，3}，{0，0})的可分性传播模型：

(6)

但是，在测试的过程中发现，对于KNOT密码算法的S盒，当I={0，2}，C={1，0}或者|I|=3时，算法2中构建的模型是无解的。这说明固定这些位置后，S盒的可分性轨迹不是一个凸集。为了构建这些情况下S盒的可分性模型，需要计算出此时S盒每一位的输出表达式，然后利用“复制”“与”“异或”运算的可分性模型来构建此时的S盒的模型。以I={0，2}，C={1，0}为例，此时S盒的输出表达式如下：

(7)

(8)

同理，可以得到|I|=3时对应的可分性模型。

对于解密方向的KNOT的S盒，可以使用同样的步骤得到S盒的可分性传播模型。需要注意的是，当I={0，1}，C={0，1}或者|I|=3时，解密S盒对应的可分性轨迹TS-1(x|I，C)不是凸集，需要计算出此时KNOT逆S盒每一位的输出表达式，然后利用“复制”“与”“异或”运算的可分性模型来构建此时的S盒的模型。

3.2 基于可分性和标志位技术的KNOT-256置换可分性模型构建方法

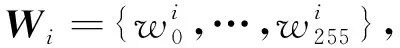
KNOT_Division_Encryption_one_Round(i，M，ai，bi，ai.F，bi.F)

和 KNOT_Division_Decryption_one_Round(i，M，ai，bi，ai.F，bi.F) ，

其中，参数i代表加密或解密的是第几轮，参数M代表可分性的MILP模型，ai.F代表模型变量ai对应的标志位，bi.F代表模型变量bi对应的标志位。算法3给出了第i轮KNOT-256加密方向可分性的MILP模型构建方法，解密方向与上述同理。

算法3第i轮KNOT-256加密的可分性MILP模型构建方法。

① KNOT_Division_Encryption_one_Round(第i轮加密，模型M，ai，bi，ai.F，bi.F)：

②ai.F=ai.F⊕RC[i]。

③ 对于j从0到 63 重复执行④：

⑤ 对于j从0到63重复执行⑥到：

⑥I=[]，C=[]。

⑦ 对于j1从0到3，重复执行⑧到⑩。

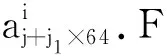
⑨ 将j1添加到集合I中；

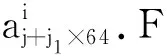
算法4构建KNOT-256置换的n1+n2轮零和区分器。

① KNOT_Zero_Sum_Distinguisher(n1，n2，V)：

② 定义两个空的可分性模型Me和Md。

③ 对于集合{(0，256]-V}中的每一个元素i，重复执行④到⑥：

⑦ 对于集合V中的每一个元素i，重复执行⑧到⑨：

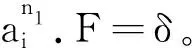
⑩ 对于i从0到n1- 1，构建KNOT-256解密方向轮函数的可分性的MILP模型：

对于Wn1中的非活跃的位置，都赋值为常数0，利用算法4，可以得到20轮到30轮的KNOT-256的零和区分器。在相同的活跃位置的条件下，与不添加标志位得到的结果进行了对比，部分得到的结果见表6(求解器：Gurobi 8.0；编程语言：Python 2.7；运行环境：Intel Core i7-5500U 2.4GHz)。

表6 KNOT-256零和区分器

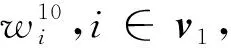
(9)

通过上面的讨论可知，在利用可分性质构造零和区分器的过程中，笔者提出的方法考虑了固定的常数对区分器的影响，而这种影响可以通过标志位技术引入可分性的模型的构造中。相比于普通的可分性建模方法，笔者构建的模型更精确，并且求解的速度更快。但是，当攻击轮数进一步提高后，由于在模型中加入了大量的限制条件，这样会超过计算机的求解能力，从而导致模型求解的时间加长，甚至不能在有限的时间内返回模型的解。这也是许多区分器自动化搜索算法面临的问题。如何解决这个问题还需要进一步研究。

4 结束语

笔者给出了分组密码算法S盒的新可分性模型的构建方法，同时基于KNOT-256算法的S盒性质和算法结构，设计了KNOT-256算法的零和区分器的自动化搜索方法。研究结果表明：KNOT-256置换存在30轮的零和区分器。尽管上面的分析不能对KNOT认证加密算法的安全性构成威胁(分组长度是256 bit的版本的初始化轮数为52轮)，但是给出了构造KNOT算法零和区分器的新方法及实用分析工具。