三元多项式展开式系数、幂、最短路经之间的联系
2021-01-28 06:56任茜钰王楠沈稷伦任泽慧
锦绣·下旬刊 2021年3期
任茜 钰王楠 沈稷伦 任泽慧

摘要:虽然杨辉三角针对两个未知数和的多次方运算说明了它与系数的相应关系及最短路径之间的关联,但其对于三个未知数的多次方并没有简便算法可以快速计算。此文在于拓展杨辉三角内容,可以做到快速拆分三个未知数多次幂的式子。
关键词:杨辉三角;多次系数;三维;最短路径
1 三元多项式及其系数的关系
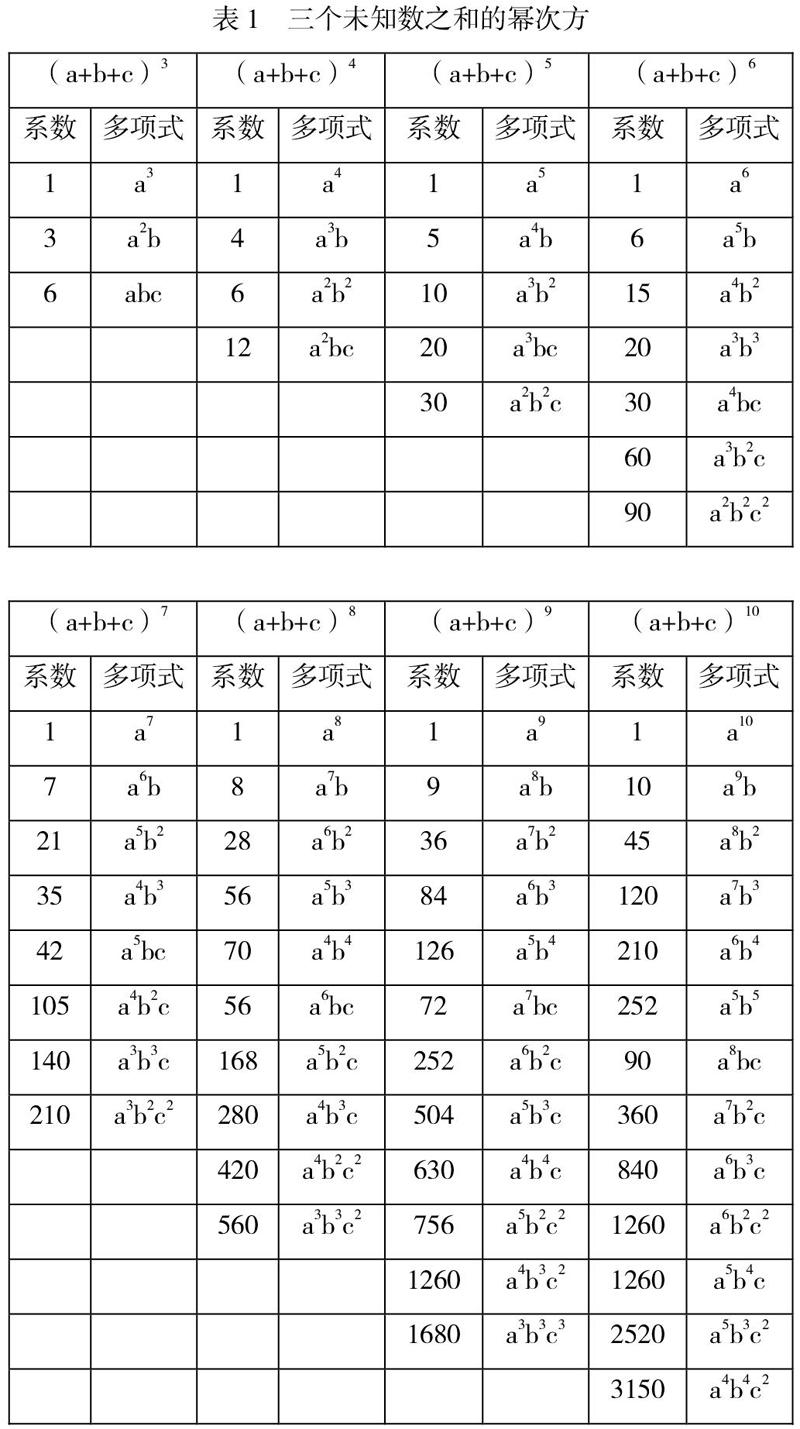
杨辉三角具有对称性,而前人已经证明。验算出的式子如表1所示。观察每项未知数的指数,可以得到项的分组规律:若有m个未知数的n次方的算式,以一个未知数为一组,从最高指数n开始依次递减,到m个未知数指数相同或相邻为止,m个未知数便是m组,系数从小到大依次排序,且某项指数越集中到一个未知数,系数越小。
2 系数之间的关系
将两个未知数的N次方系数取二分之一(第一行),三个未知数的N次方取三分之一(第二行),如图1所示。
观察图1可得到此任式定理:
其中第一个C式为原二项式,T式本文定义为三项式增量,三元n次多项式系数开始满足于二项式,直到n=2m为止。
3 系数与最短路径的关系
如图2所示,如a2bc,那么对应的坐标便是(2,1,1),则此点的最短路径数便是系数12,在x,y,z轴上的平面仍满足二项式定理,而三维图形内部的数值则为与之相连的数值之和。
4 结论
本文经过推理和研究,得到了关于三元N次方系数与多项式之间的关系,通过计算后本人也发现了多元N次方同样有此规律。
(遼宁工程技术大学软件学院 辽宁省 兴城 125105;阜新市实验中学;3.抚顺市四方高级中学)
猜你喜欢
现代商贸工业(2016年24期)2017-01-13
未来英才(2016年1期)2016-12-26
电脑知识与技术(2016年28期)2016-12-21
电脑知识与技术(2016年28期)2016-12-21
电脑知识与技术(2016年23期)2016-11-02
电脑知识与技术(2016年18期)2016-11-02
科学与财富(2016年28期)2016-10-14
科技视界(2016年14期)2016-06-08
物联网技术(2015年11期)2015-11-26
物联网技术(2015年7期)2015-07-21

