基于小波变换的非侵入负荷事件检测算法研究
乔适苏,蔡 慧,谢 岳,陈徐笛,郭 倩
(中国计量大学 机电工程学院,浙江 杭州 310018)
随着社会的发展,用户负荷类别增多,当多种电器同时运行时,对电器的识别难度加大,常规的负荷辨识方法通过在用电负荷端安装传感器监测单一电器用电情况,而非侵入负荷监测技术在总线端即可监测用户电器用电情况[1]。非侵入式负荷识别技术开发的主要目的在于实现非侵入条件下对用户用电负荷的在线识别,对电器的使用状况和用电行为进行监测和分析,能提供给电器精细化管理更多的实际数据,如用户需求响应、能效管控和电价策略等,这是对合理用电进行分析的事实依据[2]。从前对用户负荷状态数据进行检测,主要的检测方式是在用户家中安装电力检测感应器,这种设备的安装,不仅数量多,还比较占空间,给用户带来很多不必要的困扰,而对于电力公司来说,安装监控设备的成本投入较大,无法对用户进行全面覆盖。所以,对非侵入式负荷监测系统的研究成为当前热点[3-4]。
非侵入负荷监测技术主要分为数据采集、事件检测、特征提取、负荷监测,事件检测在其中起到至关重要的作用[5]。在确定用电负荷是否运行后,可对负荷进行特征提取和负荷识别分析。目前非侵入负荷事件检测方法主要有:文献[6]使用家用电器电流周期变化检测的方法判断负荷变化;文献[7]使用统计过程中常用算法广义似然比检验GLR算法;文献[8]使用基于滑动窗的双边累积和事件检测累积和(cumulative sum,CUSUM)算法,运用优化累计和算法检测负荷投切事件;文献[9]使用卡方事件检测方法;文献[10]使用基于贝叶斯信迭代的事件检测方法;文献[11]使用基于极值点(Maximum and Minimum Points,MMP)的事件检测算法。上述事件检测方法会存在漏检、误检以及参数较难设置的问题。
文献[12]提出小波分析用于事件检测能够降低随机误差,使事件检测准确率得到提高。本文对运用小波变换进行负荷事件检测的方法进行改进,利用小波分解后细节系数模值的二阶差分变化进行对负荷投切事件及电器模式改变进行定位,避免直接使用细节系数难以确定阈值的问题,通过实测数据对二阶差分事件检测结果进行准确性判断。该方法有助于提高事件检测的准确性,同时有助于分析用户用电行为,引导用户实现合理化用电和节能。
1 小波变换原理与分析
1.1 连续小波变换原理
小波变换与傅里叶变换相比,傅里叶变换只具有频域特性,小波变换具有时频特性,有利于分析某一时刻的情况[13]。
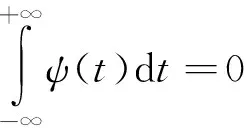
(1)
(2)
其中,k是样本指数,h0和h1是低通滤波器和高通滤波器。
小波变换可以通过对尺度函数和小波函数进行分析,对f(t)进行连续小波变换公式如下:
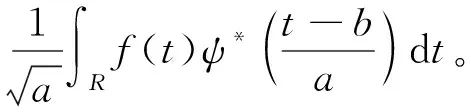
(3)
式(3)中,
(4)
<*,*>表示内积,a>0为尺度因子,b为位移因子,*表示复数共轭,ψa,b(t)称为小波基函数。
WTf(a,τ)为小波变换系数,尺度因子a用来伸缩基本小波ψ(t),位移因子b则反映位移情况。
1.2 离散小波变换原理
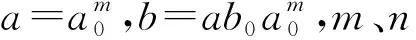
(5)
相应的离散小波变换(Discrete wavelet transform,简称DWT)可以表示为[15]
(6)
小波变换的分解层数由式(7)确定[16]:
(7)
式(7)中,fs为信号采样频率,f0为基频。
2 基于小波变换二阶差分的事件检测算法
2.1 数据预处理
用电负荷的有功功率通过每个周波的平均功率计算得到,公式如下:
(8)
式(8)中,u(t)、i(t)分别表示电压、电流的瞬时值,本文的采样频率为1.6 kHz,基频条件下每个周波的采样点数为32,将上述公式可以改写为离散化的计算式如下:
(9)
本文对有功功率进行特定的标准化处理,由于日常家用电器一般情况下最大电流值不会超过16 A,则有功功率变为
(10)
式(10)中,U基频电压为我国家庭额定电压220 V。
2.2 小波变换奇异性检测
信号奇异点位置一般指的是信号突变,信号突变的主要特征是信号在时频域上均发生变化。小波变换可对时频域同时分析,并且对信号具有“显微”的特性,对奇异信号的识别具有独特优势[17]。
通常小波变换检测变点的方法是:在信号出现突变时,小波变换后的细节系数具有模极大值,因此可以通过模极大值点的位置反映到原始信号来确定变点位置和时间。小波模值定义为小波系数的绝对值[18]。但这种方法需要对阈值进行不断训练,计算时间长并且有可能对发生事件检测不准确。所以本文提出了基于小波变换系数二阶差分的事件检测方法。
在连续小波变换中,用一阶导数和二阶导数都可以检测出奇异点;在离散小波变换中,一阶、二阶导数变成一阶、二阶差分,用一阶差分认为最大值对应奇异点位置,而二阶差分则是负值对应奇异点位置。对于一阶差分,通常需要设置一个阈值,检测出较多的奇异点结果,然后对特征进行分析得到最终结果;对于二阶差分,不会检测出较多的奇异点,检测出的奇异点位置通常是最实际的位置,二阶差分这种方法可信度更高,因此本文通过二阶差分为负的位置确定奇异点位置。
基于小波变换系数二阶差分的事件检测流程如图1。
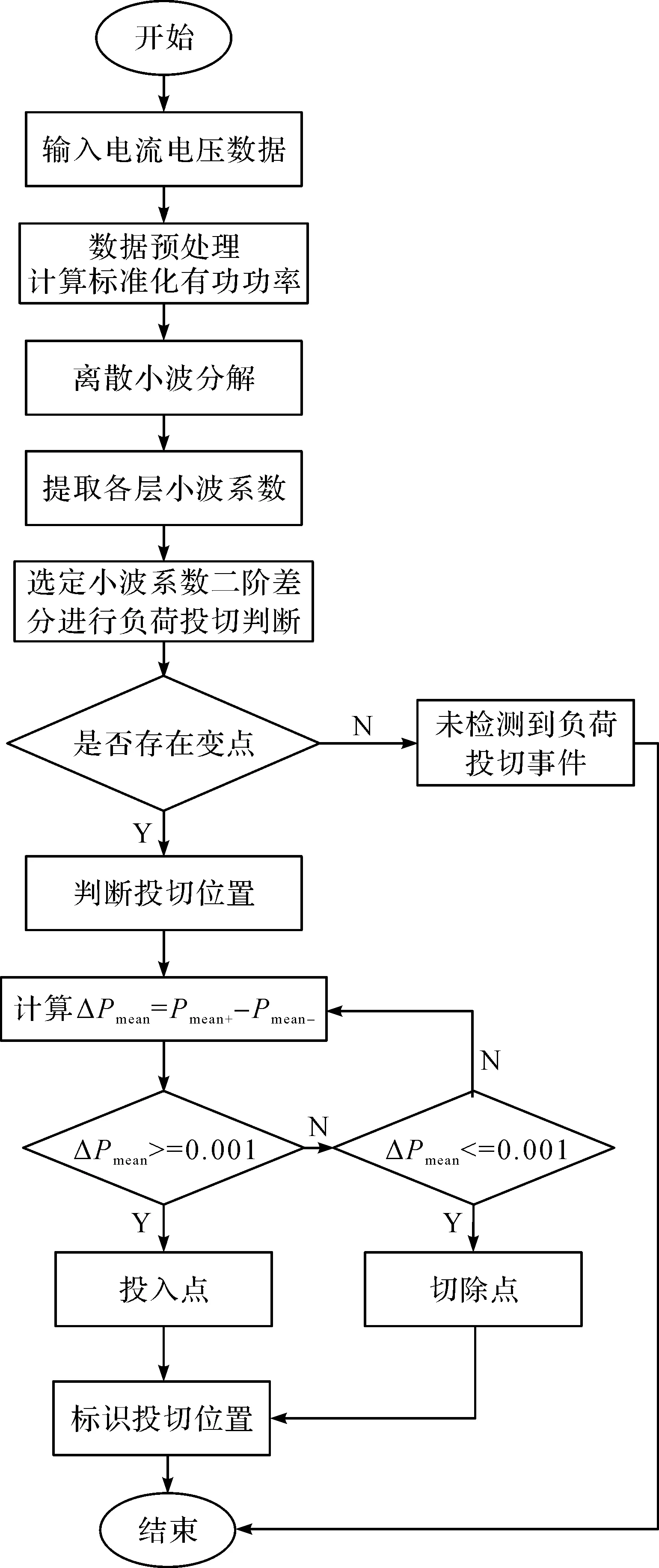
图1 小波变换事件检测流程图Figure 1 Wavelet transform event detection flow chart
2.3 负荷性质判断
在定位出用电负荷变点后,需要判断变点是负荷的投入点还是切除点。在本文中,为整体判断负荷投切,则认为负荷状态改变位置相当于负荷投切位置。利用标准化有功功率增量法进行判断:
小波变换二阶差分判断出的变点位置可以通过各层小波系数点数的改变返回到负荷的标准化有功功率曲线中,分别取标准化有功功率数据中变点前5个数据点和变点后5个数据点的平均值,设为Pmean-和Pmean+,则标准化有功功率增量的计算公式如下:
ΔPmean=Pmean+-Pmean-。
(11)
如果ΔPmean≥0.001,则判定该变点为负荷投入点;如果ΔPmean≤-0.001,则判定该变点为负荷切除点。
3 实例分析
为验证上述方法的正确性,本文使用MatlabR2016b编程软件分析。运用采样频率1.6 kHz的实验室采集数据进行实验,实验对象为常见家用电器。
3.1 单电器事件检测
采集白炽灯、电饭煲、吸尘器3种电器投入切出时刻电压电流数据,进行标准化功率计算。以上三种电器类型分别属于电阻类、电热类、电机类。
3.1.1 白炽灯事件检测
首先对实测的白炽灯单独运行的数据进行分析,通过白炽灯波形确定小波基函数及细节系数层数。白炽灯是一种短暂态过程典型开关型负荷,通过白炽灯波形确定小波基函数及用来判断变点的小波系数。白炽灯启动进入稳态以及关闭的电流波形及有功功率波形如图2,白炽灯标准化有功功率如图3。
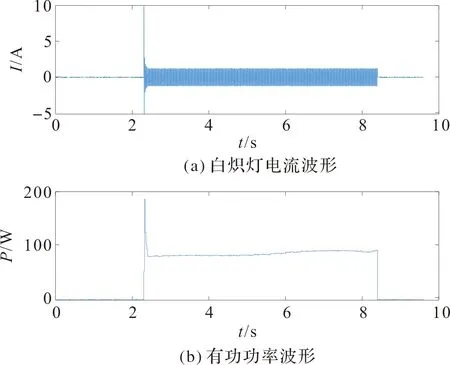
图2 白炽灯电流、有功功率波形Figure 2 Current and active power waveform of Incandescent lamp
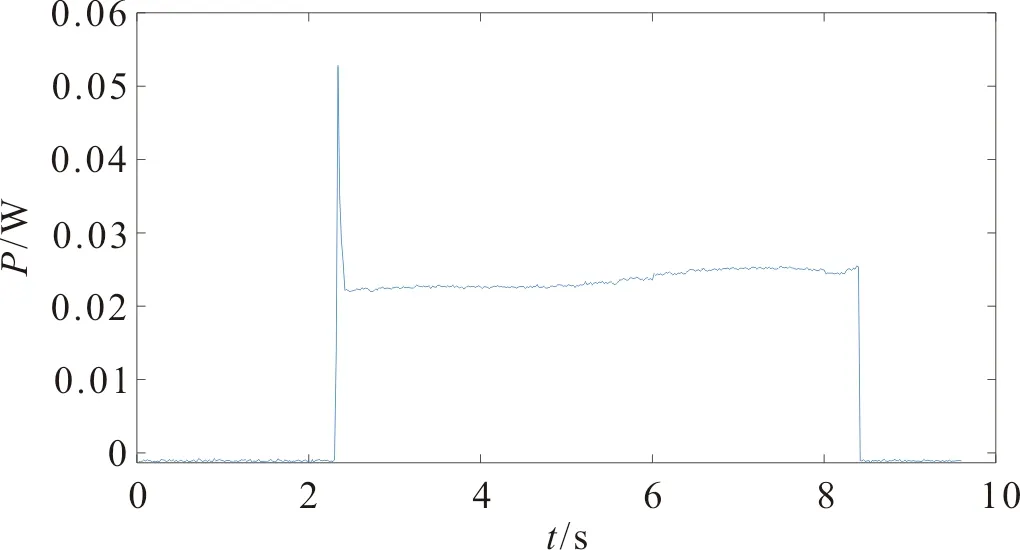
图3 白炽灯标准化有功功率波形Figure 3 Standardized active power waveform for incandescent lamps
我国家庭用电基频频率为50 Hz,根据式(7)确定,dn=4(取整数),由此频带划分为4层,小波函数的分解层数为3层。
使用db2小波基函数对白炽灯标准化有功功率数据进行离散小波分解,各层小波系数模值如图4。横坐标为小波分解后各层系数点数,对应整个过程采样时间。采用普通二进小波变换对信号进行分解,由于输入信号分别与高低通滤波器进行卷积计算,所以每次分解信号都会在上一次基础上减半。
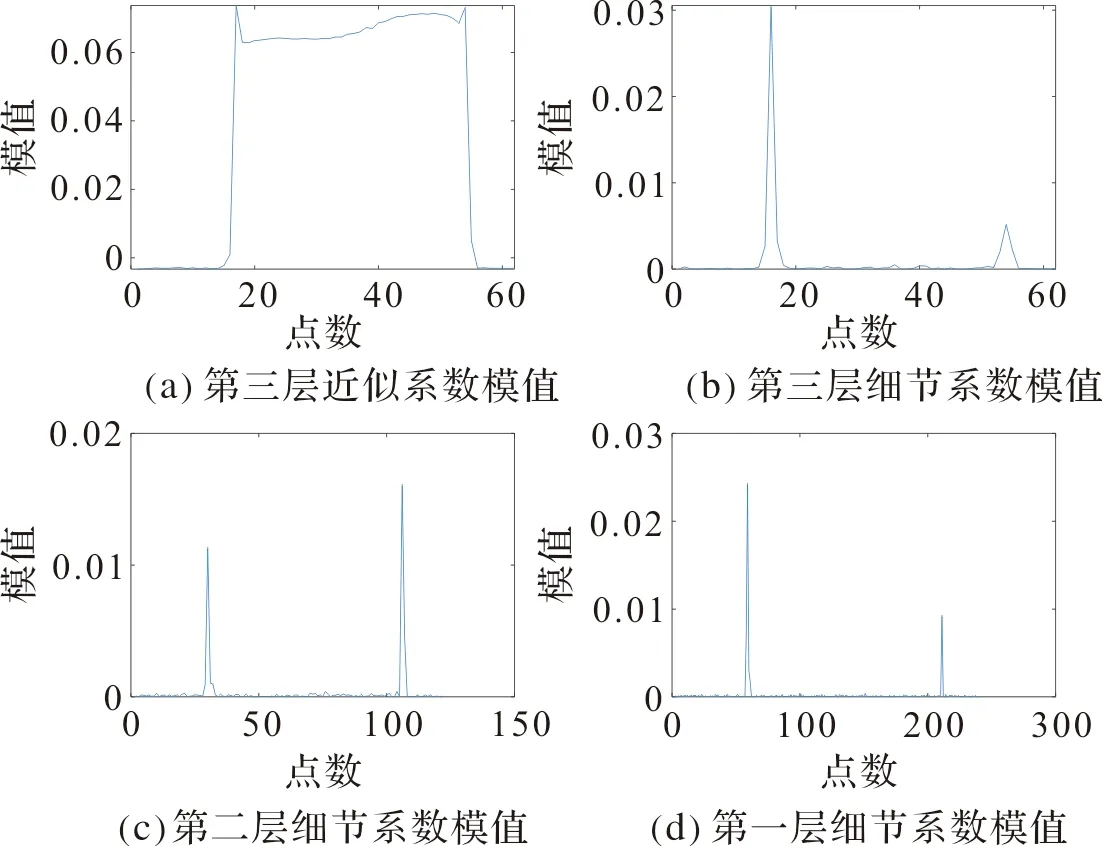
图4 白炽灯离散小波分解系数模值Figure 4 Digital-analog image of discrete wavelet decomposition system for incandescent lamps
由图4看出,细节系数具有明显的变化,但各层小波细节系数的变化均较为清晰,所以需要对各层细节系数投切定位的相对误差进行分析。
白炽灯实际启动周期为第41个周期,实际关断周期为第320个周期。db2小波分解各层细节系数定位的相对误差如表1。
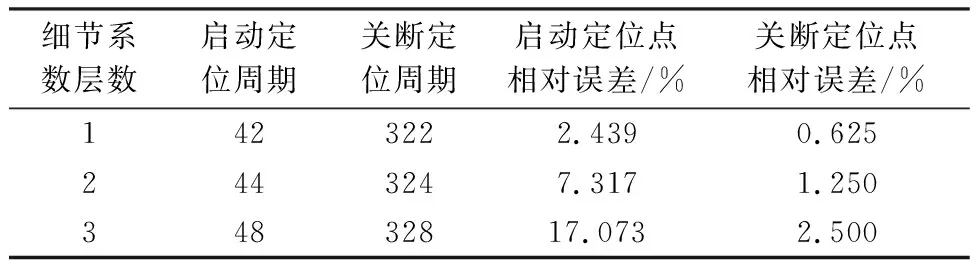
表1 各层小波细节系数白炽灯变点定位相对误差
由上表可知:第一层到第三层小波系数层数增加,投入和切除点位点处的相对误差增大。第一层细节系数启动和关断点的定位相对误差均最小。因此,本文选择小波分解后第一层小波细节系数变化作为判断投切位置的准则,后续不再考虑其他层的细节系数。
对常见小波基函数进行测试,实验结果如表2。
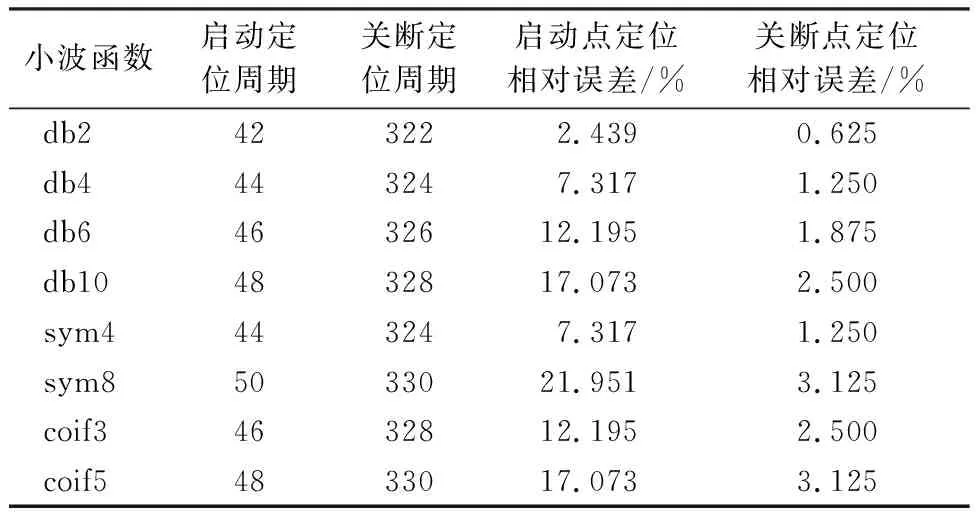
表2 常见小波基函数白炽灯变点定位相对误差
由于haar小波无法检测出变点,所以表2中不列入haar小波。由上表可知:分析8种常见小波基函数,db2小波定位投入点及切除点相对误差最小,说明db2小波对信号奇异点的辨识能力较好,对投切位置定位更准确,并且db小波基函数适用于分析多种信号类型,所以本文采用离散二进制db2小波作为基小波对信号进行分析,后续不考虑其他小波基函数。
根据式(11),投切点1的ΔPmean计算结果为0.262 7,该点为投入点;投切点2的ΔPmean计算结果为-0.257 0,该点为切除点。
3.1.2 电饭煲事件检测
运用本文事件检测方法对短时间内状态切换电流相差较大的电器进行测试,电饭煲保温状态与加热状态切换时相对电流差较大,属于有限状态型负荷。因此,选择电饭煲作为典型电器判断变点。
电饭煲保温—加热—保温—关闭的电流波形及有功功率波形及有功功率波形如图5,电饭煲标准化有功功率如图6。
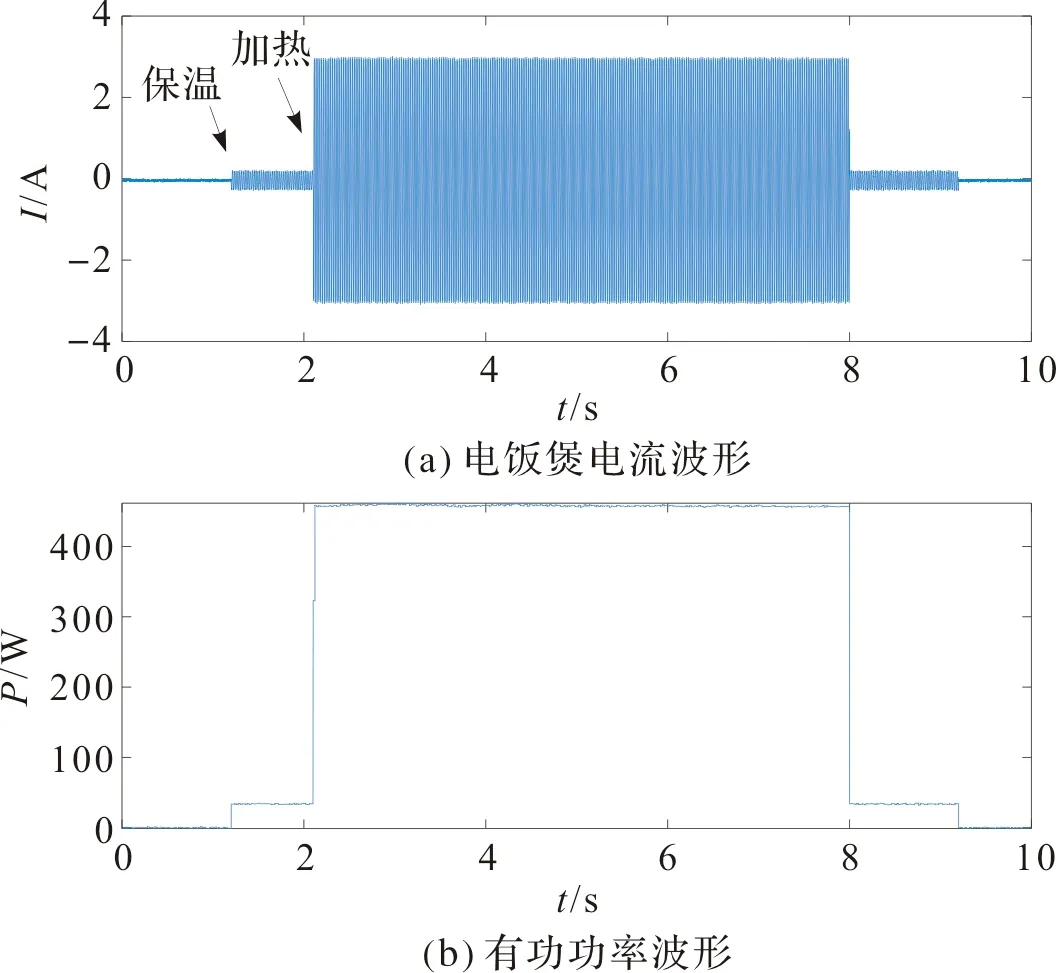
图5 电饭煲电流、有功功率波形Figure 5 Current waveform and active power waveform of Rice cooker
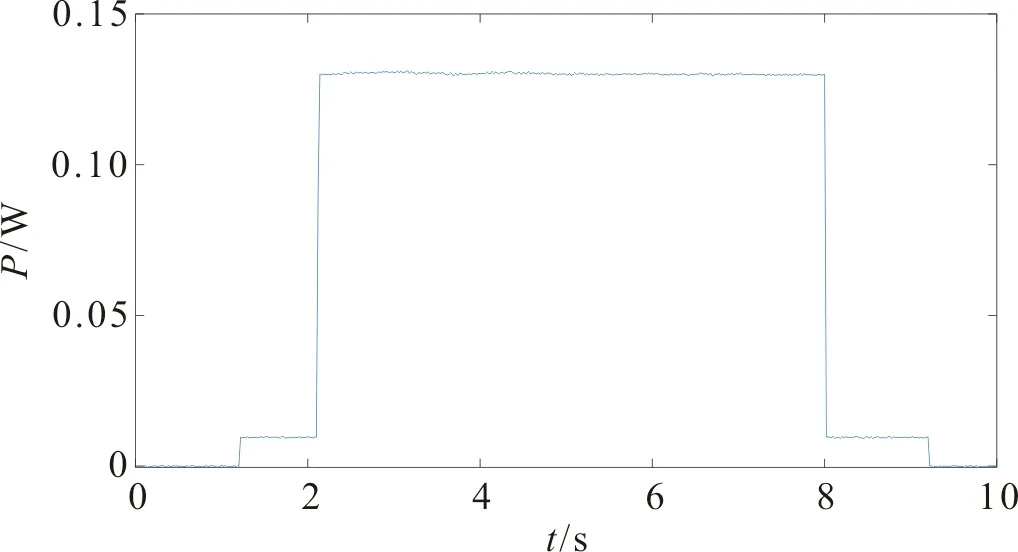
图6 电饭煲标准化有功功率波形Figure 6 Standardized active power waveform for Rice cooker
电饭煲离散小波分解后各层小波系数如图7。
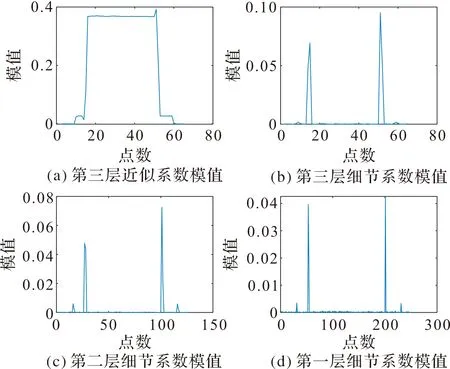
图7 电饭煲离散小波分解系数模值Figure 7 Digital-analog image of discrete wavelet decomposition system for Rice cooker
本文使用采样频率为1.6 kHz的相同数据进行不同方法的比较。发现使用小波分解系数进行事件检测需要对小波系数进行阈值选择,而阈值的选择误差易造成的负荷投切事件的漏检和误检,所以本文选择小波系数模值的二阶差分变化进行对负荷投切事件及电器模式改变的进行定位。二阶差分方法不需要确定精确的阈值,若二阶差分小于零,则该点为信号突变点。由于负荷信号小波变换后会产生毛刺,为去除毛刺影响,本文中设置极小的阈值来确定负荷变点,阈值定为-0.001。该阈值无需反复训练,适用于常用典型电器。二阶差分方法避免了直接使用细节系数难以确定阈值以及可能造成事件检测不准确的问题。
电饭煲第一层细节系数模值二阶差分图像如图8。
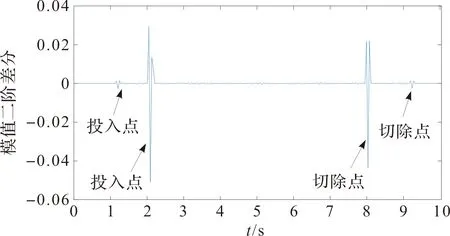
图8 电饭煲第一层细节系数模值二阶差分Figure 8 The first detail of the rice cooker is the second order difference of mathematical model value
从二阶差分图像可以清楚的判断出电饭煲运行具有4个投切位置,由式(11)计算得到4个投切位置的性质如下:
ΔP1=P1+-P1-=0.048 3,
(12)
ΔP2=P2+-P2-=0.443 7,
(13)
ΔP3=P3+-P3-=-0.600 8,
(14)
ΔP4=P4+-P4-=-0.047 8。
(15)
投切点1、投切点2为投入点,投切点3、投切点4为切除点。
电饭煲的事件检测结果验证了小波变换二阶差分事件检测的方法可以在大电流状态和小电流状态依次变化时均能准确检测。
3.1.3 吸尘器事件检测
运用本文事件检测方法对短时间状态切换电流相差较小的电器进行测试,吸尘器暂态过程相对较长,暂稳态切换时相对电流差较小。因此,选择吸尘器作为典型电器判断变点。
吸尘器投入—暂态—稳态—切除电流波形及有功功率波形如图9,标准化有功功率图像如图10。
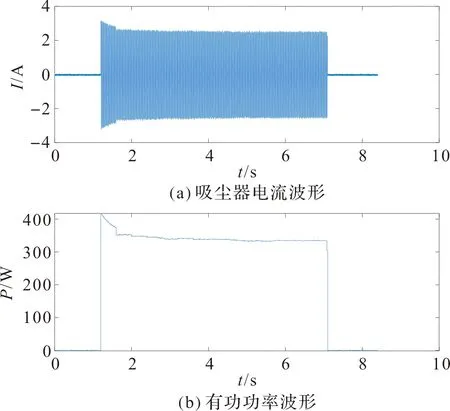
图9 吸尘器电流、有功功率波形Figure 9 Current waveform and active power waveform of The vacuum cleaner
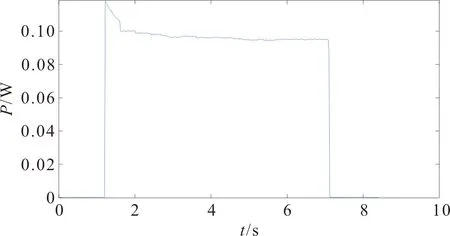
图10 吸尘器标准化有功功率波形Figure 10 Standardized active power waveform for The vacuum cleaner
吸尘器离散小波分解后各层小波系数如图11。
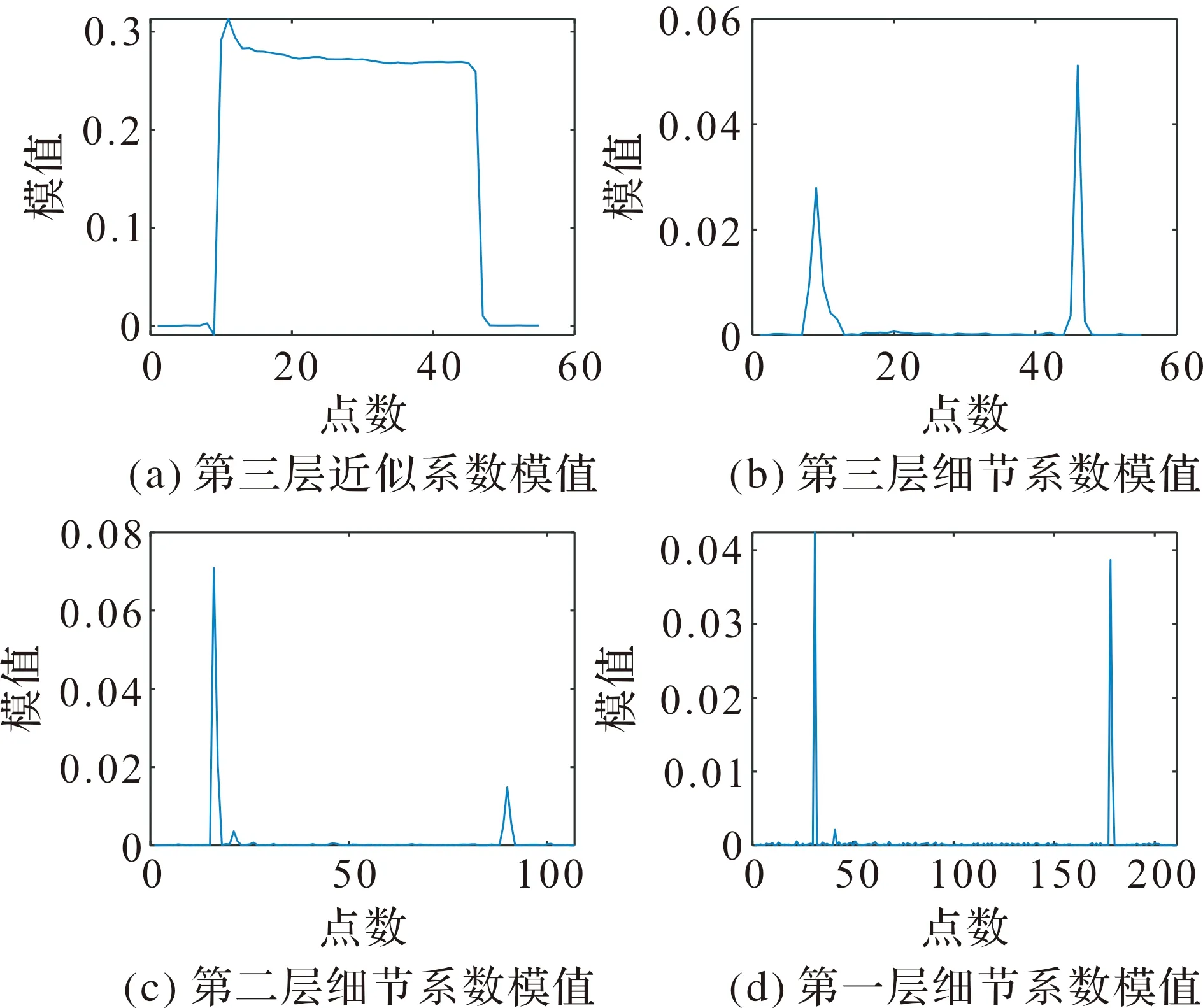
图11 吸尘器离散小波分解系数模值Figure 11 Digital-analog image of discrete wavelet decomposition system for vacuum cleaner
吸尘器第一层细节系数模值二阶差分图像如图12。
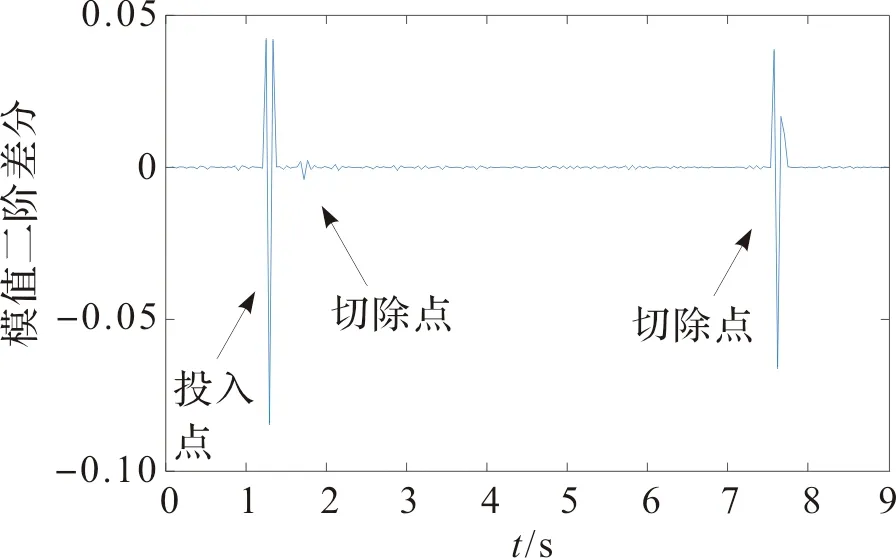
图12 吸尘器第一层细节系数模值二阶差分Figure 12 The first detail of the vacuum cleaner is the second order difference of mathematical model value
对比图11、图12再次证明:细节系数模值难以确定阈值,无法定位进入稳态时间,二阶差分方法则克服这一缺点。
由式(11)计算得到3个投切位置的性质如下:
ΔP1=P1+-P1-=0.288 7,
(16)
ΔP2=P2+-P2-=-0.019 1,
(17)
ΔP3=P3+-P3-=-0.192 9。
(18)
投切点1、投切点3为投入点,投切点2为切除点。由吸尘器二阶差分图可以看出,即使负荷暂稳态切换并不明显,电流差较小,暂态过程持续时间相对较长,二阶差分方法仍然可以对其进行准确定位,对电器发生的状态改变做出准确判断。
3.2 多电器事件检测
单电器运行通常不符合实际情况,所以需要对多电器运行情况进行分析。
本文多电器数据采集流程:第5 s开启电饭煲进入保温状态后进入加热状态,30 s后开启白炽灯,5 s后开启微波炉(微波炉运行中存在自身状态转换),微波炉运行20 s后关闭微波炉,10 s后电饭煲加热切换至保温至关闭,10 s后关闭白炽灯。多电器电流波形如图13。多电器标准化有功功率图像如图14。
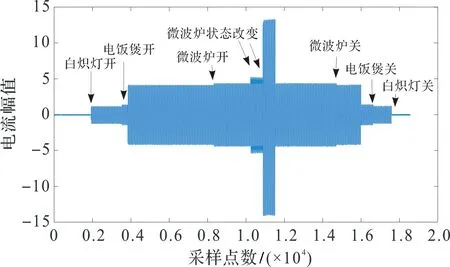
图13 多电器电流波形Figure 13 A variety of electrical operating current waveform
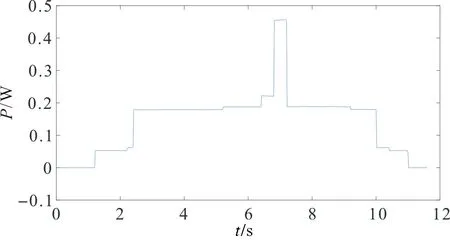
图14 多电器标准化有功功率波形Figure 14 A variety of electrical standardized active power waveform
由图13和图14可以看出:在多电器的情况下,电器变化在短时间内较多,不同电器电流变化较大,对有功功率进行标准化可以十分清晰地反映出电器细微的变化,便于后续小波变换的判断。
多电器第一层细节系数模值二阶差分图像如图15。
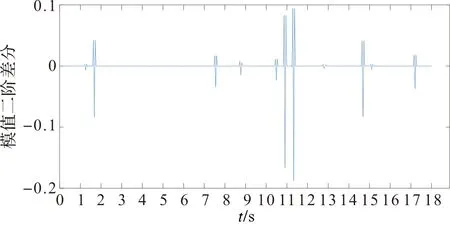
图15 多电器第一层细节系数模值二阶差分Figure 15 The first detail of the vacuum cleaner is the second order difference of mathematical model value
本文发现当电器每次动作间隔在0.3 s以上时,本方法有较好的检测效果。当有3种电器运行,共有11次动作时,通过多电器小波变换第一层细节系数二阶差分,11次动作全部检测,证明了小波变换事件检测方法在多电器运行的情况下依旧有良好的检测能力。
多电器投切位置判断准确性结果如表3。

表3 多电器事件检测结果
由表3可知:在该组实验下,检测到11个投切点,该组别事件全部检出;经过多次实验,该方法事件检出率达到93%以上。该组实验下,定位周期判断仅在第8个投切点有1个周期误差。实验结果证明:小波变换二阶差分事件检测方法具有优越的检测准确率,算法误检、漏检率低,对功率相差大的电器有较强的检测敏感度,并且有较好的运算速率,因此,基于小波变换的事件检测算法具有良好的可行性和可信度。
4 结 语
对负荷事件进行检测是非侵入负荷监测管理系统中的关键技术环节,对负荷事件的准确定位能够为负荷识别打下良好基础。本文首先对小波变换检测变点的理论进行了研究,将有功功率进行特定标准化,计算小波分解层数,并且选定最优小波基函数和最优小波系数。在小波变换模极大值理论的基础上,提出了运用小波变换细节系数的二阶差分变化定位负荷投切位置的方法,并用标准化有功功率增量法对变点的性质进行判断。通过多次实测电器运行数据的结果表明,本文所提出的方法参数设置简单,避免了阈值选择的问题,并且对不同负荷事件均有较强适应能力;能够准确有效地检测用电负荷投切事件的发生并且定位发生位置、判断变点性质。本文事件检测方法计算方便、快捷,为提高智能电表非侵入负荷监测的准确性打下基础。
本文主要实现电器投切事件检测功能,未涉及具体电器识别,今后在本文方法的基础上运用机器学习算法实现非侵入负荷监测,以及进一步优化该方法在复杂电器情况下的检测准确率是后续工作的完善方向。

