ROCE模型在互联网企业价值评估中的运用
方晓成
(马鞍山职业技术学院 经贸系,安徽 马鞍山 243000)
互联网行业投资活动频繁且投资金额巨大,而错误的估值和预测将会导致数以亿计的损失。因此更为精准适用的价值评估方法是增加互联网行业潜在投资规模与推动新兴经济发展的重要保障。传统的价值评估方法包括市场法、现金流量折现法以及由金融期权估值技术所衍生出的实物期权估值法。但上述模型缺少对互联网企业发展模式中用户基础与网络效应两大核心因素的直接体现,故而运用于互联网企业价值评估的结果并不让人满意。因此如何将网络效应与用户基础融入价值评估模型成为本领域一个重要的研究方向。
一、以用户为基础的现金流量折现模型
用户生命周期价值这一概念来源于营销领域。最初它被定义为一名用户在其整个生命周期里购买商品的价值的总和。但这一界定忽视了用户对其他产品的购买即交叉销售所带来的现金流、推荐其他用户所带来的正面或负面影响等。随着营销认知的深入,用户生命周期价值的内涵也不断得以扩充。Bauer和Hammerschmidt[1],Kemper[2]先后将用户生命周期价值与企业价值融合,构建和丰富了以用户为基础的现金流量模型。这一类模型站在一个更为微观的视角去预测企业的现金流,同时通过用户数量、保持率等元素凸显出用户基础对于互联网企业的重要性。但因为与传统的现金流量折现法存在相似的理论基础,当模型运用于创业初期的互联网企业时仍然存在历史数据不足以及对未来变动中潜藏价值反映的不足。虽然通过推荐价值在一定程度上体现了网络效应,但由于有效计量的缺失通常假定推荐价值大于等于零。这忽略了用户可能会引发的负面效应。
二、基于用户的实物期权模型
(一)用户数量变动模型的构建
奥兹·谢伊完整阐述了网络效应的内涵[3],即产品价值随购买该产品及其兼容产品的消费者的数量增加而增加。因此在具有网络效应的产业中会表现出“先下手为强”和“赢家通吃”的市场特征。而互联网、传媒、航空运输、金融等行业普遍存在该特征。
同样Krafft也观察到互联网行业发展中的这一现象。一家互联网企业在它最初进入市场时,如果用户的数量能够超越一个特定的市场临界值,那么它的用户数量大概率会以指数形式增长。在达到巅峰状态后会和传统行业的企业一样进入平稳的持续发展阶段,反之则会创业失败,用户数量以指数速度下降。可以据此构建以用户为基础的实物期权模型(Real Option Customer Equity Model)[4]。
为拟合互联网企业用户数量发展的特征,krafft构建了一个反向均值回归的模型如式(1)所示:
(1)
(二)ROCE模型的理论计算方法
Krafft提出使用二叉树的方式来模拟计算用户数量变动的随机过程[4]。见式(2):
(2)
其中k代表在用户数量增加或减少的绝对值,j代表在变动过程中所处的某一个状态。为确保二叉树临近状态变动后的数量能够重合,公式中设定各节点用户数量按照相同的幅度k增加和减少。
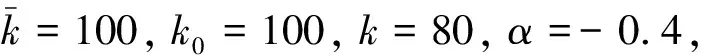
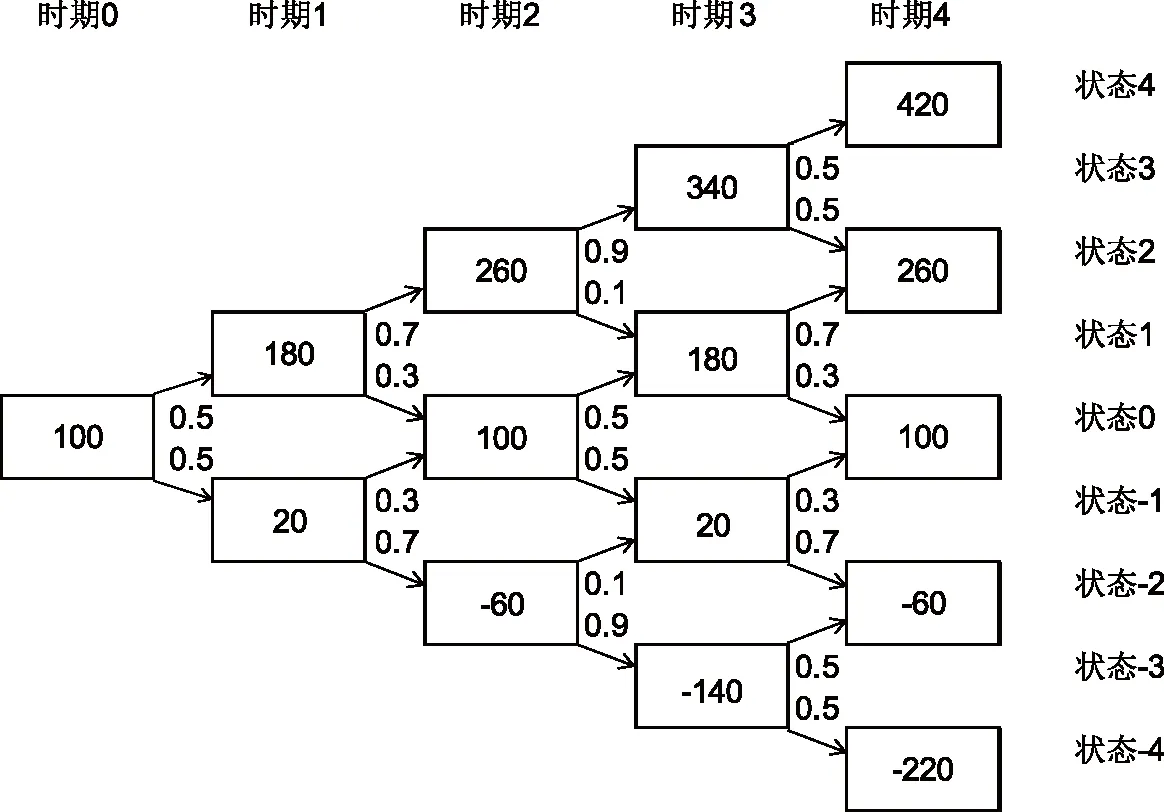
图1 用户数量变化
以时期4、状态4的用户数量420为例,它是从最初的100开始,经过4个时期4次向上增加后达成的用户数量。各节点向上的概率根据如下的公式计算。该公式通过变动概率满足用户数量变动期望的方法推导而来。如式(3)所示:
(3)
图1中数量为负数的情形显然是不合理的。更为恰当的处理是增加一个破产的条件设定。既当用户数量为负时,意味着公司已经破产。这一破产条件比传统的实物期权模型中设定现金流为零时企业破产更符合互联网企业的特征。
同时krafft认为当一家互联网企业处于积极的反馈效应中时,增加的不仅仅是用户的数量。还会导致每一名用户所创造的现金流也随之而上升。反之单位用户创造的现金流会减少,即用户现金流的变化与用户数量的变动保持同方向等概率。基于这一假定将单位用户在状态j时创造的现金流定义为式(4):
cj=c0(1+g)j
(4)
在一个c0=1,g=5%的案例中
c4=1×(1+5%)4=1.2155
通过把各个时期和状态下的用户数量与单位用户现金流相乘获得相应的企业现金流。如图2所示:

图2 所有用户各期现金流变化
在假定时期4之后用户不再为企业带来现金流的前提下。可以按照公式(5),通过倒推的方式计算出当前时期下企业的价值。
(5)
以时期3状态3这一节点的企业价值计算为例,当折现率为10%时
由于第4期时用户带来现金流的最后一期,因此对于第4时期而言企业的价值等于当期用户创造的现金流。
Krafft所构建的ROCE模型相对于传统估值模型更好地突出了用户数量的迅速扩张对互联网企业生存的重要性,体现了用户数量增加及用户现金流中潜藏的的网络效应。但模型实际运用时相关参数的确定是一个亟待解决的问题。
三、模型的参数估计及运用
(一)σ(0)波动率的估计
在ROCE模型中σ(t)代表t时期某一变动节点用户数量的波动率,它是一个变动的参数。在二项式模拟用户数量变化时并不需要专门去确定每一个节点上的变动率,只需要确定初始状态下的波动率σ(0)并将其用于参数k的估计。
根据传统财务中以股价历史数据计算波动率的做法,可以选取评估对象企业或者是类似企业过去13个周期的用户数量的变化来计算历史的波动率。以腾讯QQ月活跃账户数量为例,假设评估的初始点为2020年年初,则可以按照如下方式估计σ(0)。
根据腾讯所公布的数据,过去13个季度的QQ月活跃账户数量变化如表1所示:
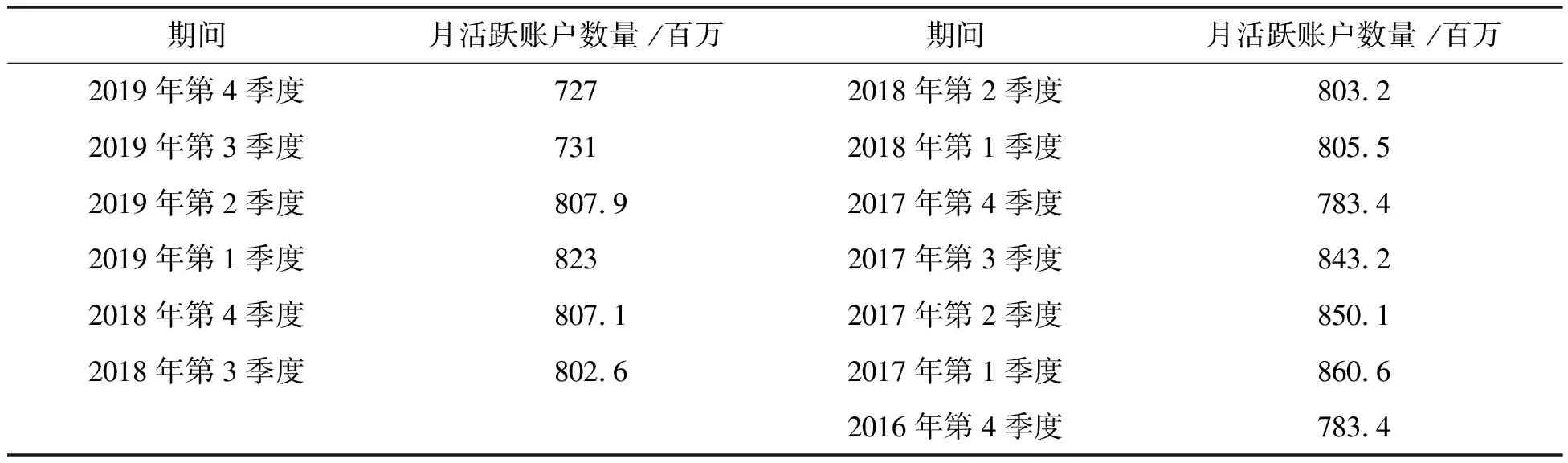
表1 QQ月活跃账户数量变化
假设评估初始点的用户数量变动波动率σ(0)将于历史波动率保持一致,则qq月活跃用户的波动率取值为35。对于创业初期的互联网企业来说,由于受到经营周期长度的影响很难取得过去12个季度的历史数据。在这种情况下,选取历史12个月的数据来作为波动率计算的样本更为可行(如表2所示)。
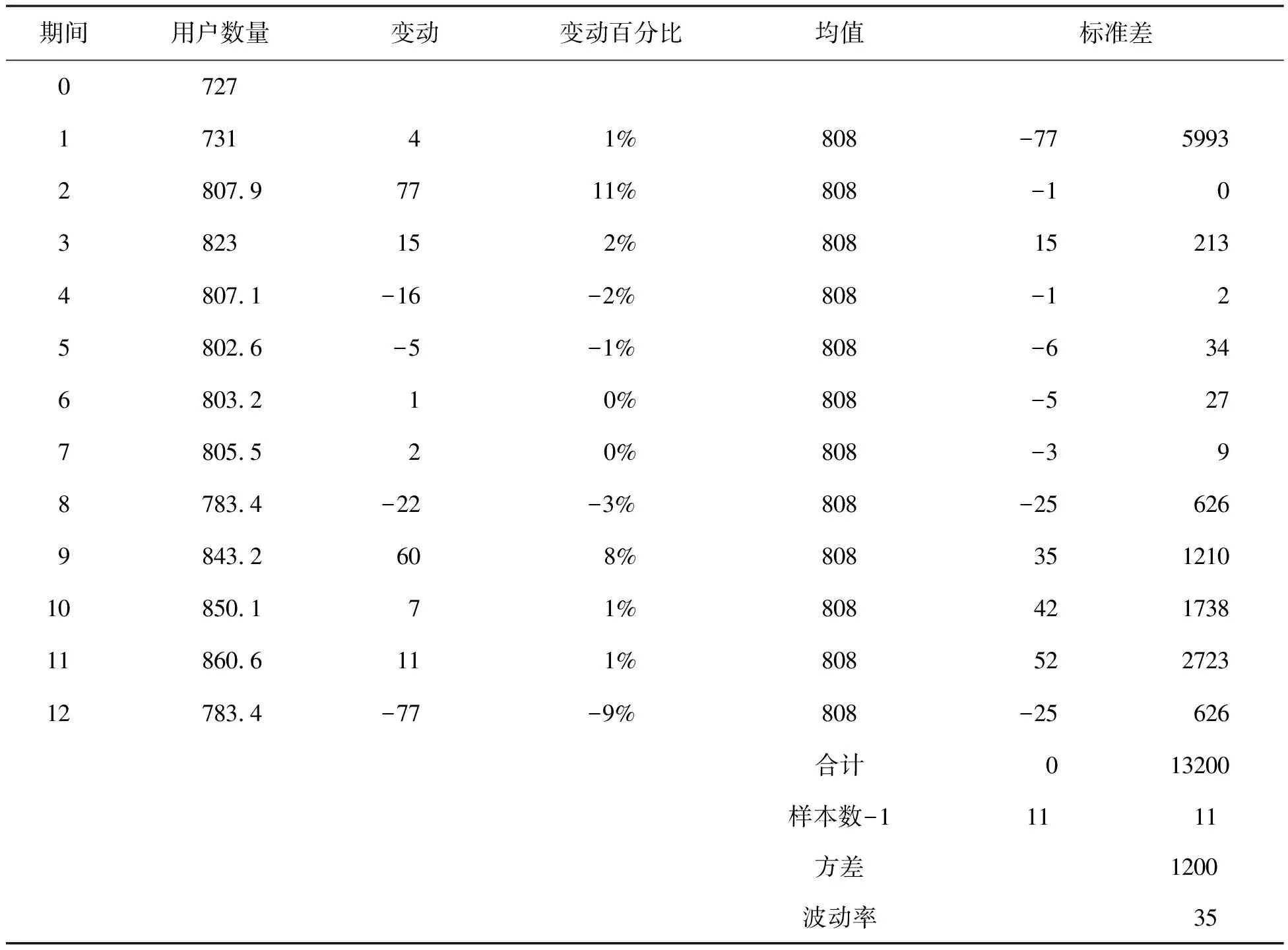
表2 历史波动率计算表
(二)用户数量变动幅度k的估计
Hull通过选取u与d使二叉树与波动率吻合的方法,确定了金融期权中金融资产价值上升比率u和下降比率d[6]。在本模型中也可以采用相似的方法确定用户数量变动幅度k。
用户数量变动的波动率可以按照公式(6)计算:
σ2=E(X2)-E2(X)
(6)
由于ROCE模型中假定各节点上升下降的幅度一致均为k,则代入评估初始点各具体参数后公式(6)可以写成:
σ2=P0k2+(1-P0)(-k)2-(P0k+(1-P0)(-k))2
(7)
而初始评估点的的σ2已根据历史数据予以确定,公式(7)可以进一步表述为:
P0k2+(1-P0)(-k)2-(P0k+(1-P0)(-k))2=σ2(0)
(8)
根据公式(3)可知:
(9)
将公式(9)代入公式(8)当中可以推导出
(10)
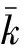
(三)企业价值的反向推算
在krafft用于模型演示的案例中,每位用户的现金流在第四期终止。但现实中用户的现金流是会持续发生的。拓宽这一设定的第一种方式是假定在未来特定时期,互联网企业将会进入平稳发展的阶段。新用户的增加与老用户的流失保持均衡,即用户的总数量不再增加。每位用户所产生的现金流也保持不变。以图2中的现金流为基础,假定从第四周期开始进入平稳发展期形成永续现金流,则各个节点上企业价值如图3所示:

图3 永续现金流量下企业价值
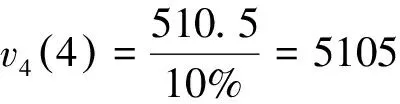
这种处理方式潜在的问题在于,当预测期间较多时反向推算的计算量将大幅增加。尤其是对于初创期互联网企业以月为周期进行变动模拟时。
为简化计算过程可以采用第二种方式,以图1中的用户数量为基础并将负数替换为零,假定其中的4个周期对应的是一年的四个季度。则通过反向推算可知对于初始评估点而言,第四季度末的用户数量期望为152。第二年用户数量的变动便以152为初始值展开二项树模拟,各预测年度以此类推。二项树的构建也仅针对每年的四个季度进行推演,从而达到减少二项树演变步骤的目的。
四、结论