改进提升小波阈值法在MEMS陀螺仪误差分析中的应用
景冰洁,韩跃平,张 鹏,徐文武
(1.中北大学信息与通信工程学院,山西太原 030051;2.中北大学仪器与电子学院,山西太原 030051)
0 引言
微小型三轴稳定平台是一种利用惯性MEMS器件在被控对象受到外界干扰时对其进行控制,使其在惯性空间的状态保持不变的仪器,并且微小型三轴稳定平台能够按照给定控制命令进行惯性空间中的转动[1-3]。而稳定平台陀螺仪测量信号中的随机噪声是影响性能的重要因素之一,如果能将噪声从稳定平台陀螺仪的测量信号中分离出来,则可提高陀螺仪测量信号的信噪比,有助于性能改善。
小波变换在时域、频域都具有表征局部信息的能力,能够很好地保留有用信号,比较适合信号的分析与处理。Donoho和Johnstone等在20世纪末首次提出了软、硬阈值去噪法,这种方法虽然计算量小,实现简单,但是硬阈值造成附加振荡,产生跳跃点,门限阈值处不连续,软阈值在重构信号时产生均方差很大,与真实信号相比,产生一定的偏差。在此之后,许多学者在阈值及阈值函数的构造方面做了大量的研究。基于传统硬、软阈值函数去噪的缺点上,学者们又相继提出半软阈值函数、软硬阈值折衷函数、自适应阈值函数等都对信号处理做出了贡献。
由于稳定平台的陀螺仪输出信号随机噪声具有长相关、非平稳等特性,本文提出改进提升小波阈值去噪法对稳定平台的陀螺仪输出信号进行去噪,可达到输出精度提高的目标。
1 微小型三轴稳定平台构成及误差分析
微小型三轴稳定平台是一款应用于实验教学,同时又具有标定测试功能的仪器。其具有防抖隔振、稳瞄稳像、目标跟踪等功能,该平台集多个功能于一体,包括稳定平台、三轴位置转台、三轴速率转台、摇摆台,一机多用,相较于传统的测试标定转台具有体积小、成本低的优点。
如图1所示,微小型三轴稳定平台由一系列MEMS器件组合而成,惯性传感器模块包括三轴MEMS陀螺仪、三轴MEMS加速度计、三轴MEMS磁强计、主控制器。该模块负责采集惯组姿态信息,并将姿态信息传输至上位机。平台结构模块优化了大型稳定平台的结构,使稳定平台更加小巧、灵活。控制模块是稳定平台的核心,一方面将陀螺仪、加速度计、磁强计采集的数据进行解算处理,另一方面控制电机及驱动模块,使平台保持平稳。电机及驱动模块主要执行控制模块的命令,在舵机驱使下保持航向外框、俯仰中框、横滚内框始终稳定。上位机模块可以显示惯性测量单元IMU姿态,加速度计、陀螺仪角速率信息;还可控制角度/速率,位置模式、摇摆模式等运动模式。
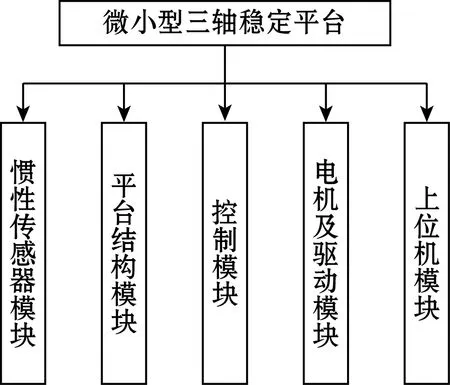
(a)组成结构框图

(b)实物图
分析稳定平台陀螺仪的误差来源,其构成元件的性质、结构的连接形式以及环境变化等因素给稳定平台陀螺仪的输出造成误差干扰[4]。误差主要有以下方面:
(1)MEMS器件误差。由MEMS陀螺漂移引起的零位漂移、输出漂移及稳定漂移;
(2)安装误差。主要有三轴稳定平台框架的安装误差及陀螺仪的安装误差;
(3)其他误差。信号传输误差、控制电路等存在的电子线路噪声等。
造成微小型三轴稳定平台的陀螺仪输出信号误差是随机误差。由功率谱密度分析可知,这种随机误差属于高斯白噪声。而小波阈值去噪法计算量小,实现简单,非常适合信号中混有高斯白噪声的情况,能剔除原始信号绝大部分的随机噪声。
2 小波阈值去噪算法
2.1 提升小波变换的基本原理
20世纪90年代中期,Sweldens等提出一种小波构造的新方法叫提升小波。后来,该方案逐渐形成了“第二代小波”。
提升小波直接在时(空)域分析信号,不依赖Fourier变换。提升小波具有既可以保留小波特性,又能打破小波原有的局限,还能够包容传统小波的优点。
提升小波变换基于小波提升算法构建小波变换,其核心是以Mallat算法为基础,采用提升算法中的预测与更新算子对原始信号数据进行小波正变换和反变换,继而得到不同分辨率下的小波变换结果。
提升小波变换可分为分解和重构两部分[5-6],正变换中,主要包括分裂、预测以及更新3个部分:
(1)分裂(split):将输入信号fi按奇偶性分为偶数序列ai+1与奇数序列di+1。
fi+1=fi,2n,di+1=d1,2n+1
(1)
(2)预测(predict):由于信号的局部相关性,引入一预测算子P并利用偶数序列ai+1去预测奇数序列di+1,得到奇数序列的一个预测值dj+1,m,该预测值称其为小波系数。
dj+1,m=dj+1-P(aj+1)
(2)
(3)更新(update):采用一更新算子U对偶数序列ai+1进行更新后得到一个更新结果aj+1,m,该结果即为提升小波的尺度系数。
aj+1,m=aj+1+U(dj+1,m)
(3)
提升小波反变换则包含反更新、反预测以及合成3个部分,与分解过程相反。
2.2 小波阈值去噪基本原理
带噪信号在时间域连续,而在小波域,有效信号分解得到的小波系数模值较大,噪声对应的小波系数往往很小,因此,通过设置阈值对每尺度小波分解得到的小波系数进行处理,小于阈值的小波系数的模滤除,保留大于等于阈值的小波系数的模,然后将保留下来的小波系数进行重构,可以得到去噪后的信号[7]。小波阈值去噪法的去噪实质就是利用小波变换把含噪信号分解到多尺度上,然后在每一尺度下把属于噪声信号的小波系数去除,保留有效信号的小波系数来重构去噪后的信号。小波阈值去噪法原理如图2所示。
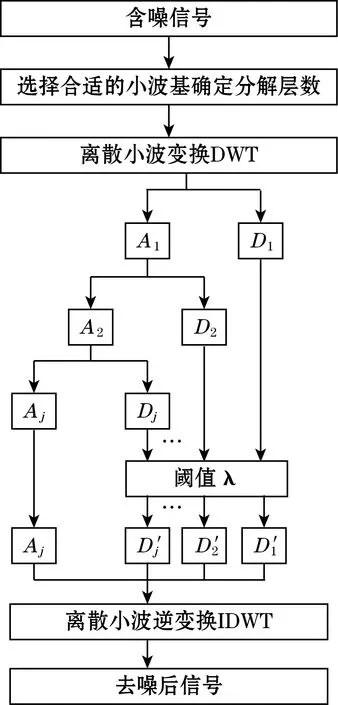
图2 小波阈值去噪算法流程图
2.3 改进提升小波阈值去噪法
综合以上条件,本文选择db4小波,分解层数j选为3是比较合适的。图3为小波工具箱中的db4小波。
图3 小波工具箱中的db4小波
2.3.1 改进阈值
采用合理的阈值λ,对MEMS陀螺仪信号进行量化。小波阈值去噪的步骤中,最关键的是如何选取阈值并对阈值进行量化,它关系到信号去噪的质量。由于噪声得到的小波系数和信号得到的小波系数根据其大小值的区分并不明确,因此在设置适当的阈值时存在困难,阈值的微小变化将会导致由于边界突变而使重构信号产生剧烈变化。
传统的小波固定阈值[7]:
(4)
式中:N为信号长度;λ为阈值;σ为噪声的标准差,一般σ=median(|Dj,k|)/0.674 5。
从传统小波阈值公式中可以看出,阈值λ会随着信号长度N的增加而增大,极限时,阈值会非常大,将所有尺度的小波系数都置零,造成信号的缺失,去噪效果会有影响。
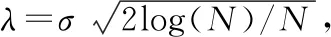
由于噪声存在于小波细节系数Dj,k,有用的信号存在于小波近似系数Aj,k,从小波分解中可知,噪声在小波细节系数Dj,k中会随分解尺度的增大而减小,因此去噪时,不同分解层的阈值λ应该不同。本文采取文献[8]的阈值选取方法,利用log(j+1)对每层的阈值进行改变:
(5)
式中:N为信号长度;j为分解层数(尺度);λ′为改进阈值。
2.3.2 改进阈值函数
选取或构造合理的阈值函数[9-14],与式(2)中的阈值对每层小波系数进行分析。传统的小波阈值函数为硬阈值函数与软阈值函数,函数表达式为式(6)、式(7)。
硬阈值函数:
(6)
软阈值函数:
(7)
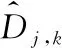
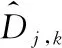
因此,为了解决传统软硬阈值函数的缺陷,本文构造一种改进小波阈值去噪函数来对三轴稳定平台的陀螺仪输出信号进行处理。改进的阈值函数如式(8)所示。
(8)
式中:λ′为改进阈值;α为α∈[0,1)的调节系数;m为正偶数。
图4为改进后阈值函数的曲线图,由图4可以看出,改进后小波阈值去噪,有以下特点:

(3)改进后的小波阈值函数对小波细节系数Dj,k是高阶可导的,且其导数都大于0,是单调不减函数。
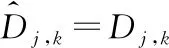
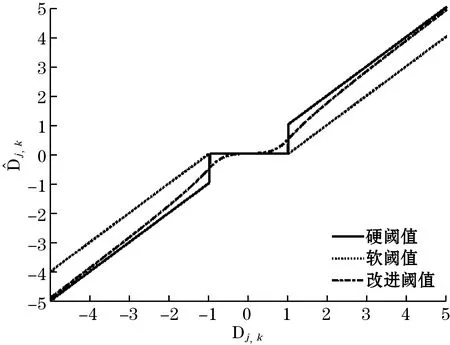
图4 3种阈值去噪算法的阈值函数曲线
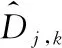
对去噪后的细节系数及近似系数使用提升小波重构的方法来得到去噪后的陀螺仪信号。
3 实验验证及结果分析
如图5所示,试验时,对微小型三轴稳定平台陀螺仪进行静、动态标定实验时需要三轴转台设备,通过上位机控制速率转台在位置模式、恒速模式、变速模式、摇摆模式等模式下运行,可实现静、动态采集测试。

图5 实验采集环境
3.1 静态数据采集及分析
由于上位机可控制三轴转台的运动模式,故通过上位机将三轴转台陀螺仪采样频率设为10 Hz,首先将三轴转台通电后预热10 min,让其运行稳定后,在保持水平的状态下通过上位机采集500 s,截取其中的250 s作为静态数据样本,即2 500个数据样本。
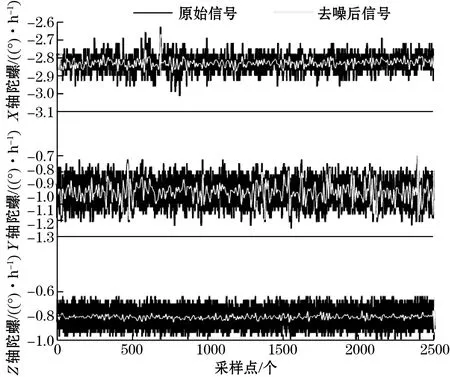
采用传统软、硬阈值去噪法及改进提升小波阈值法对三轴稳定平台陀螺仪输出的静态数据样本在MATLAB中进行处理,图6(a)为三轴陀螺仪数据经软阈值去噪算法在db4小波下经3尺度分解与重构后的前后去噪效果。图6(b) 为三轴陀螺仪数据经硬阈值去噪算法在db4小波下经3尺度分解与重构后的前后去噪效果。图6(c)为三轴陀螺仪数据经改进提升小波阈值法选取db4小波基,分解层数为3层,α=0.5,m=2,利用MATLAB中的lwtcoef函数实现提升小波变换后的前后去噪效果。
由图6(a)~图6(c)可知,在同一组静态陀螺仪数据下,经过硬阈值去噪后的信号有较多毛刺,不够平滑,波峰与波谷的振荡较强烈;而软阈值去噪后的信号相比于硬阈值去噪,去噪效果相对平滑,但与原信号相比,偏差较大;改进小波阈值的去噪图像,去噪后信号与原始信号相似度更高。
本文通过引入信噪比(SNR)、均方根误差(RMSE)、平滑度(r)[15]来定量比较去噪效果。
(9)
(10)
(11)
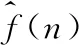
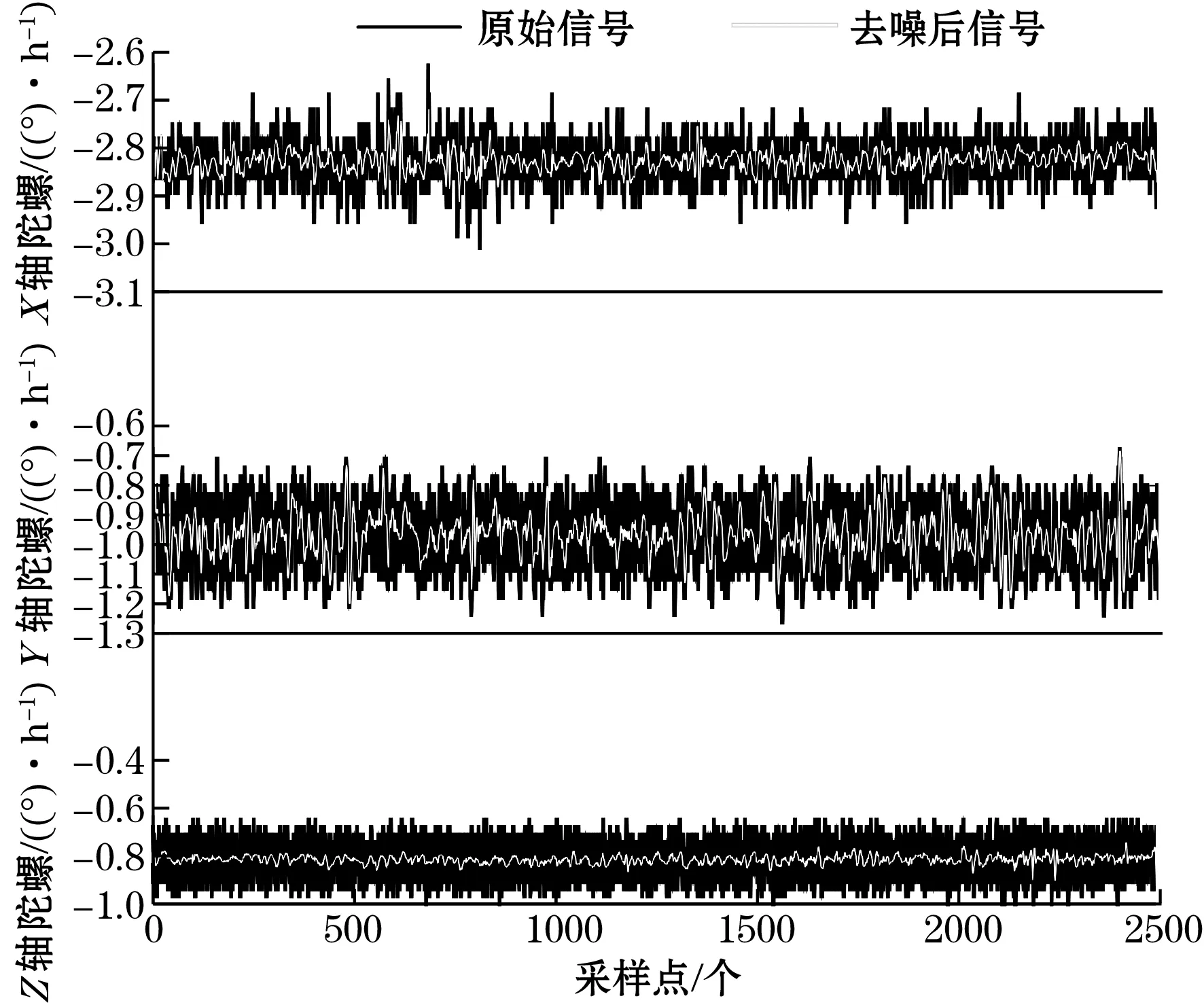
(a)软阈值去噪法去噪前后对比
(b)硬阈值去噪法去噪前后对比
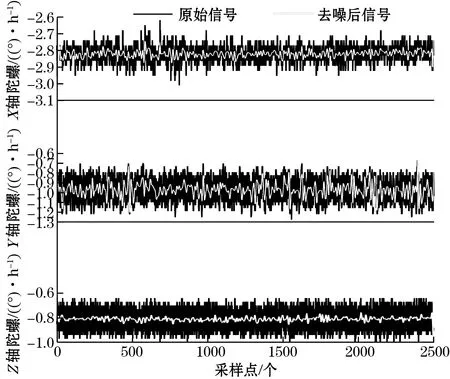
(c)改进阈值去噪法去噪前后对比图6 三轴稳定平台陀螺仪静态信号去噪效果
信噪比是原始信号功率与噪声功率之间的比值,SNR越大,混在信号中的噪声越小,去噪效果越好;均方根误差是原始信号与去噪信号差的平方和与信号长度比值的平方根,值越小,则表示偏差越小;平滑度是指去噪后信号的变化率与原始信号变化率的比值,r越小,去噪效果越好。
从表1中可以直观得出,经过改进小波阈值处理后的信号信噪比在其软硬阈值去噪基础上提升了1.61 dB左右,均方根误差相对降低了0.02左右,光滑度提高了10。
3.2 动态数据采集及分析
在采集静态数据后,为验证改进小波阈值函数对动态数据处理仍有效,同样通过上位机将三轴转台采样频率设置为10 Hz,中框和外框保持静止,在内框翻转20°的状态下通过上位机采集100 s,截取其中的50 s作为动态数据样本,即500个数据样本。
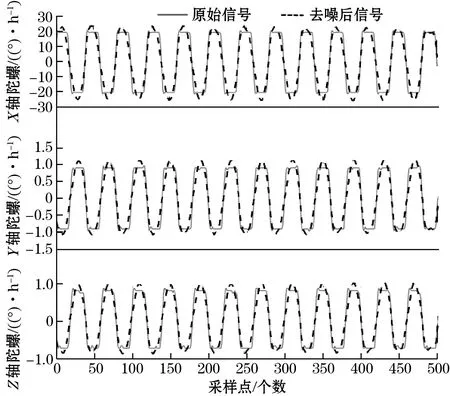
由于在动态下采集,中框和外框的陀螺仪信号也会因为内框的翻转而受到影响,但影响不大。与静态数据处理过程相同,仍采用传统软、硬阈值去噪法及改进小波阈值法对三轴稳定平台陀螺仪动态数据样本在MATLAB中进行处理,在同样的动态样本下,图7(a)为三轴陀螺仪内框翻转20°动态数据经软阈值去噪算法在db4小波下经3层分解与重构后的前后去噪效果。图7(b)为三轴陀螺仪外框翻转20°动态数据经硬阈值去噪算法在db4小波下经3层分解与重构后的前后去噪效果。图7(c)为三轴陀螺仪外框翻转20°动态数据经选取db4小波基,分解层数为3层,α=0.5,m=2,仍利用MATLAB中的lwtcoef函数实现提升小波变换后的改进提升小波阈值法的前后去噪效果。
从图7中可知,提升小波改进阈值去噪起到了更好的降噪效果,对比小波硬阈值去噪,得到的去噪后信号趋势更加明显,抑制了毛刺,减少了振荡;对比小波软阈值去噪,数据平滑且更接近原始信号。
从表2中定量得出,经过改进提升小波阈值处理后的信号信噪比提高了2 dB左右,均方根误差降低了0.02,去噪后的信号与原始信号偏差较小、光滑度好。
4 结论
本文针对微小型稳定平台陀螺仪输出信号的随

表1 3种阈值去噪方法对静态数据去噪效果比较
(a)软阈值去噪法去噪前后对比

(b)硬阈值去噪法去噪前后对比
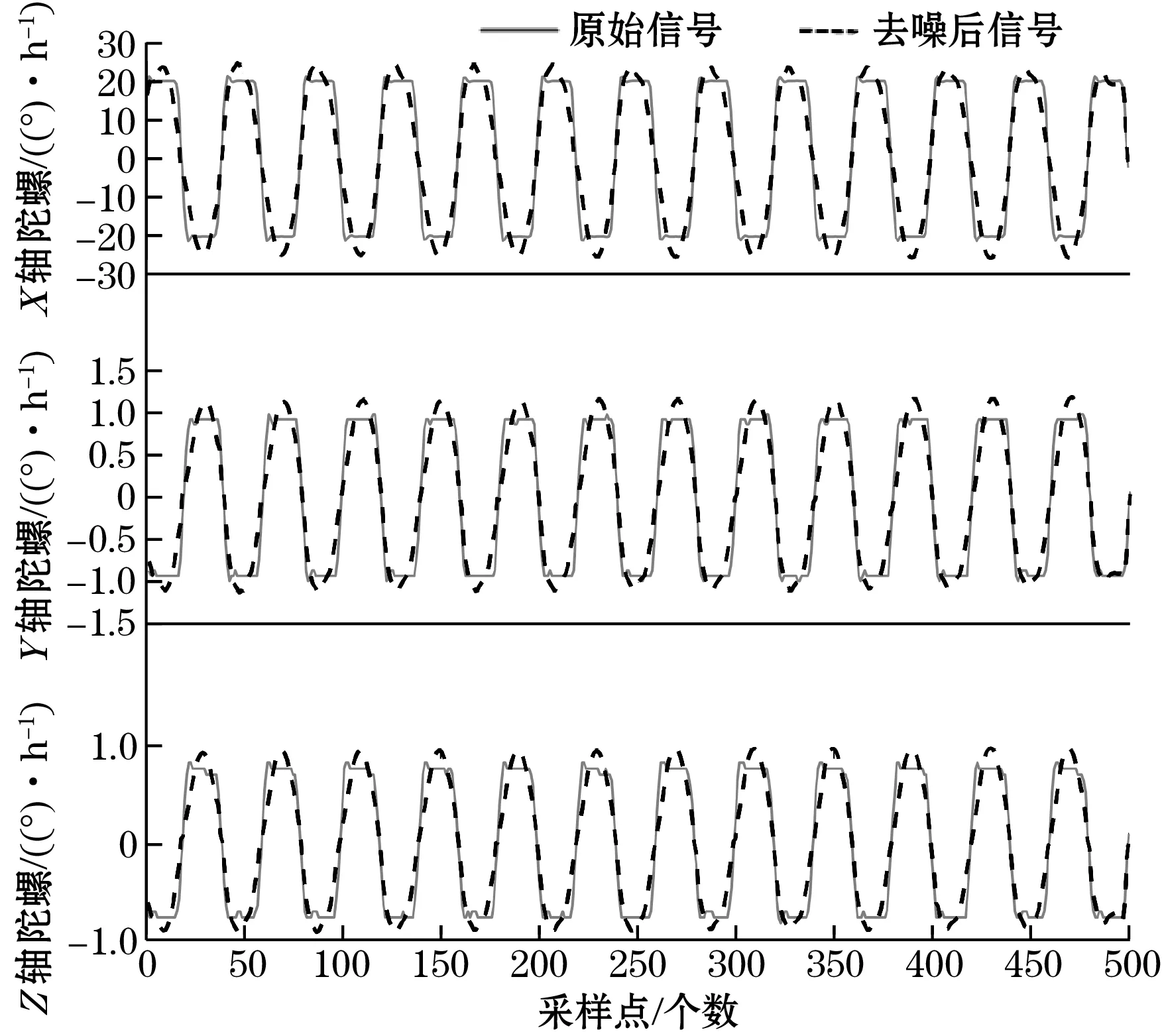
(c)改进阈值去噪法去噪前后对比图7 三轴稳定平台陀螺仪动态信号去噪效果
机误差,提出一种改进提升小波阈值去噪法,通过陀螺仪输出信号的静、动态数据仿真处理,对陀螺仪的输出信号进行分析,滤除了绝大部分随机误差。仿真结果的性能指标表明,改进小波阈值均优于软、硬阈值去噪,都能达到滤除随机误差的效果。
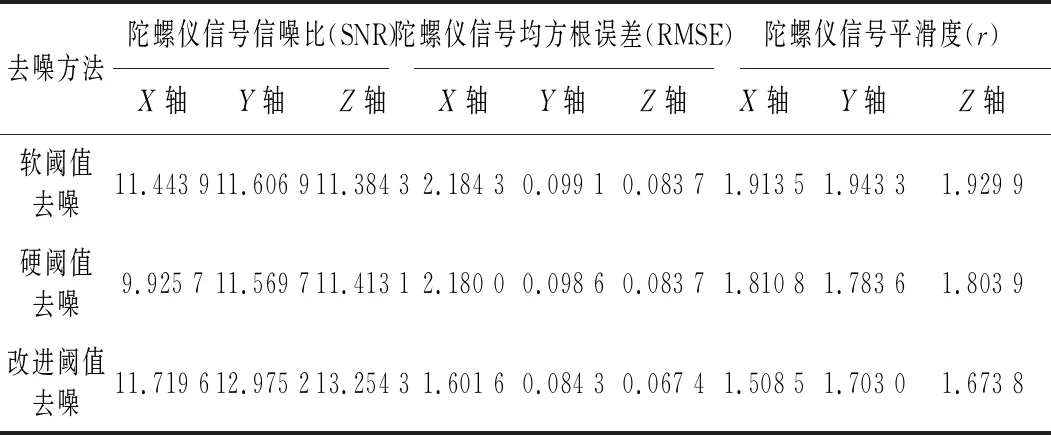
表2 三种阈值去噪方法对动态数据去噪效果比较

