考虑分布式电源接入的配电网状态检修决策优化

郭腾云,于 磊,王 和,郝国刚,宋方方

(国网冀北电力公司张家口供电公司,河北 张家口 075000)

0 引言

针对当前阶段配电网与配电网检修技术的发展趋势,在配电网检修计划的制定过程中考虑分布式电源出力的不确定性与状态检修模式是保证检修计划可靠性的必然要求。在状态检修方面,文献[1]指出状态检修能够以设备的实际健康状态为依据制定检修计划,保证检修方案的经济性和安全性。文献[2]指出状态检修能够及时、有效地安排设备检修,实现按需检修,保证可靠性和经济性。文献[3]提出一种计及设备故障风险及电网运行风险的设备状态检修决策优化模型,将设备状况与电网运行情况综合考虑。文献[4]对考虑分布式电源的检修问题进行探索,指出配电网检修计划是检修时间与负荷转移路径的联合优化问题,并给出了相应的操作原则,但是未能考虑出力的不确定性。文献[5]采用可信度理论描述不确定性,对分布式电源出力进行处理,具有一定可信度。但是采用模糊和机会约束的方法来处理不确定性,需要大量历史数据作为可信理论的依据,计算工作量较大,难以满足检修优化对负荷转移优化的要求。

针对上述问题,结合设备在线监测技术和设备状态预测技术,提出了一种新的基于检修设备集的检修方法,在检修周期内对设备集进行检修安排。构建了检修时间优化与负荷转移优化相结合的双层优化问题,在一定程度上解决了上述2个问题在配电网检修中的难点,具有一定的实际意义。

1 考虑分布式电源的配电网状态检修分析

1.1 分布式电源出力不确定性的影响以及双层优化模型

配电网中接入出力具有不确定性的分布式电源后,会对原来的检修策略制定方法产生影响,应当充分考虑。在检修过程中进行负荷转移操作后,若分布式电源出力减小,已求得的负荷转移方案有可能会出现功率不平衡、违背运行约束条件的情况,被迫进行二次负荷转移甚至切负荷。如若分布式电源出力增加,则存在更优的负荷转移方案可以消纳更多分布式电源出力,减小失电负荷。一方面要尽最大能力消耗分布式电源出力、减小失电损失,另一方面要降低违背运行约束以及二次失负荷的情况发生。

负荷转移优化做为一个具体的优化问题已经相对复杂,但是检修时间优化需要求取负荷转移操作的方案以相关成本,所以二者构成了双层优化模型。外层为检修时间优化,内层为负荷转移优化,二者相互支持,时间优化为负荷转移优化提供每个检修时段下具体检修设备的信息。负荷转移优化负责求取对应的最优负荷转移路径和相关成本,返还给检修优化,作为检修优化适应度的一部分。二者信息共享,共同完成检修计划的制定工作。

1.2 状态检修实现的相关问题

状态检修是一个根据设备状态得到检修设备集的问题。但是现阶段我国虽然在大力发展状态检修技术,但是状态检修对于配电网依然存在一定的困难。主要来自于配电网设备繁多种类复杂,无法做到每台都配备相应的在线监测设备,因此本文探索一种实时监测状态量与预测状态量相结合的求取检修设备的方法,最大程度地发挥状态检修的优势,弥补现阶段暴露出来的问题。

在状态检修的背景下,首先通过状态量的监测与预测得到检修设备集,然后对检修设备集内的设备安排检修时间优化,在检修优化过程中不断进行负荷转移优化求取相关的负荷转移方案以及成本,在所得到的检修方案中进行决策,选择最优的方案确定为最终的检修方案加以实施。

2 考虑分布式电源接入的配电网状态检修模型

2.1 动态检修设备集的确定

每一个检修周期内的动态检修设备由状态监测、状态预测两部分构成。

2.1.1 状态监测部分

对于变压器、重要线路等重要设备,已有相对配套的监测设备,能够通过设备状态量的监测数据得到设备的实时状态。

2.1.2 状态预测部分

配电网中很多设备无法实现有效的在线监测,提取这些设备的实时状态比较困难,对于此类设备,则采用状态预测的方法确定状态。设备状态预测与故障率求取的方法如下:

故障率λ是基于设备故障发生概率得到的,通过对所有设备故障发生概率的统计,得出设备的故障率。根据故障率与故障概率的关系,得出故障率的计算公式

常用的设备随时间老化的经验公式对设备的健康指数进行评估,公式如下

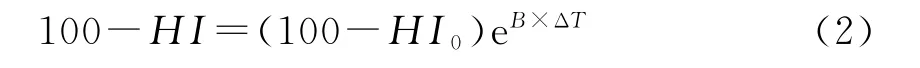
式中:HI0为设备上次评估的健康指数;B为设备老化系数;ΔT为距上次评估所跨越的时间。

将预测状态较差或者预测水平低于阈值的设备加入当期的动态检修设备集,故障率为预测状态水平确定的故障率。

2.2 基于两阶段模型的负荷转移优化方法

分布式电源出力不确定性会对调度人员制定的负荷转移方案产生影响,破坏方案的稳定性,增加成本。基于以上思路,采用两阶段模型对配电网检修中的负荷转移问题进行求解,步骤如下:

第1阶段为负荷转移方案制定阶段。该阶段根据决策者最小化负荷转移成本的思路制定负荷转移方案。根据分布式电源出力的预测值,采用节点深度编码与遗传算法相结合的方法求取预测出力水平,确定成本最低的方案

第2阶段为负荷转移成本确定阶段。该阶段根据分布式电源最大化相关成本的思路确定所得方案的成本。在给定的分布式电源出力区间内进行遍历,则所选方案的成本会随出力的变化而变化,选择遍历得到的最高成本定为该负荷转移方案的成本,而非第1阶段求得的方案。

由上述思路与步骤归纳的考虑分布式电源出力不确定性的负荷转移优化模型为

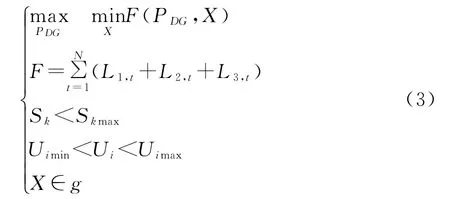
式中:N为划分时段数;X为网络拓扑结构;L1,t为t阶段的开关操作费用;L2,t为阶段t的失电费用;L3,t为网络损耗费用。Uimin,Ui,Uimax分别为节点i的最低允许电压、实际电压和最高允许电压;Sk,Skmax分别为线路k流过的实际功率和最大允许功率。X为负荷转移后配电网的拓扑结构,g为辐射状拓扑结构集合。

具体负荷转移方案的求解采用基于节点深度编码技术的方法实现[6]。在寻优过程中很好地保证了配电网的辐射状约束,避免网络分析环节,节约优化时间。

2.3 多目标的配电网状态检修优化模型

在一个检修周期内,配电网面临的风险主要有配电网的检修风险和配电网故障风险。

配电网的检修风险指的是计划内停运设备发生的相关费用,其数学表达如式(4)。

式中:ND为检修周期内包含的总的时段数;GM1(d)为时段d的设备检修费用;FM(d)为根据博弈方法得到的d时段检修工况下开关操作费用、计划失电费用、网络损耗费用总和。

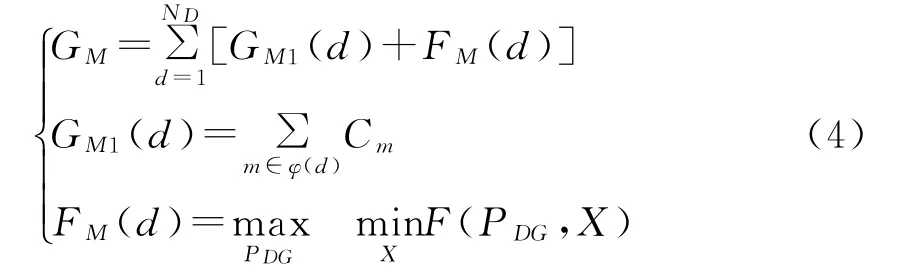
配电网的故障风险指的是计划外停运设备发生的相关费用,由于各设备会依自己的故障率发生故障,是不确定性故障,故配电网的故障风险定义为故障与相应故障概率的乘积。

其数学表达为

式中:φ(d)为时段d内故障集;ρ(h,d)为时段d内设备h的故障率;GR1,h(d)为时段d内设备h的资产损失;Ch,s为设备h的修复成本;μh(d)为相应的可修复概率;Ch,r为设备的重置成本;FR,h(d)为根据博弈方法得到的d时故障重构的开关操作费用、计划失电费用、网络损耗费用总和。

以检修时间为变量,检修风险和故障风险最小为目标的多目标优化模型如下:

约束条件在满足负荷转移相关约束的基础上,还应当考虑检修能力约束和硬性检修约束。

检修能力约束指的是检修工作受到人力、物力的限制,同时在检修的设备不得超过一定限制

式中:Ud为时段d内计划停运检修设备的数目;u为一个时段内在检修状态设备数目的最大值。

2.4 配电网状态检修方案决策模型

总体目标贴近度的决策方法可以从各目标综合角度反映目标的总体达成程度,因此可以更加客观地对检修方案给出评价。

多目标的一般形式为

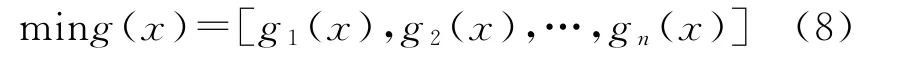
定义目标gi的正、负理想点为和。则定义单目标满意度为

目标函数g与其正、负理想点的夹角余弦为

在此基础上,构造总体目标贴近度函数

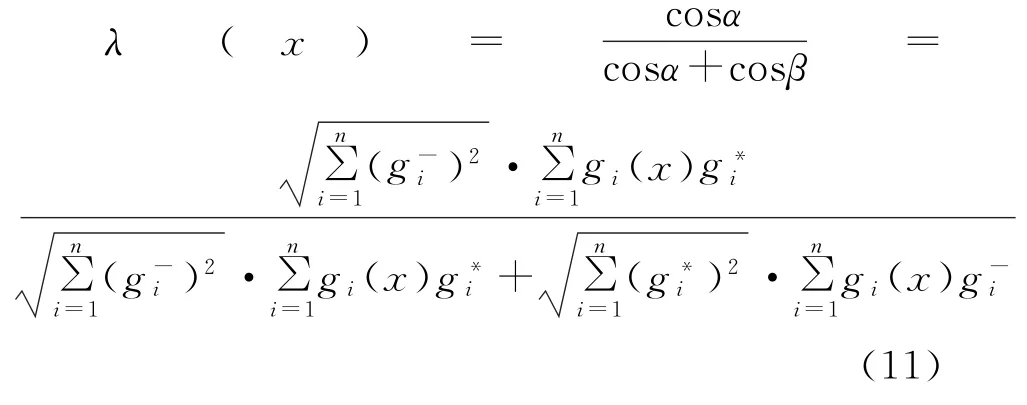
选择满足单目标满意度与总体目标贴近度的决策模型,通过人为给定单目标的最低满意程度,对2个目标同时考虑,求得的结果更加合理,其数学表达式为

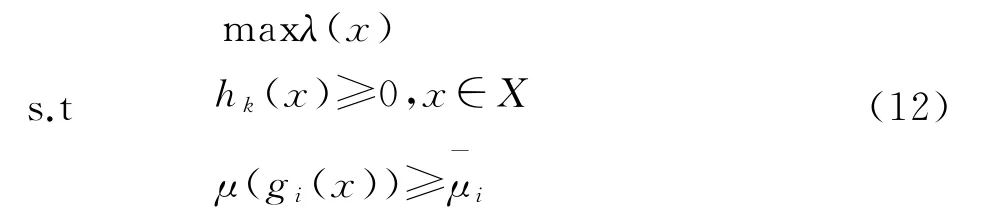
决策得到满足决策者要求的最优解,这一最优解既满足一定的单目标满意度,也综合考虑了个目标之间的均衡关系,可以作为最终的检修方案[7]。

3 状态检修模型求解

根据上述原理与模型,基于遗传算法的求解流程示意,见图1。

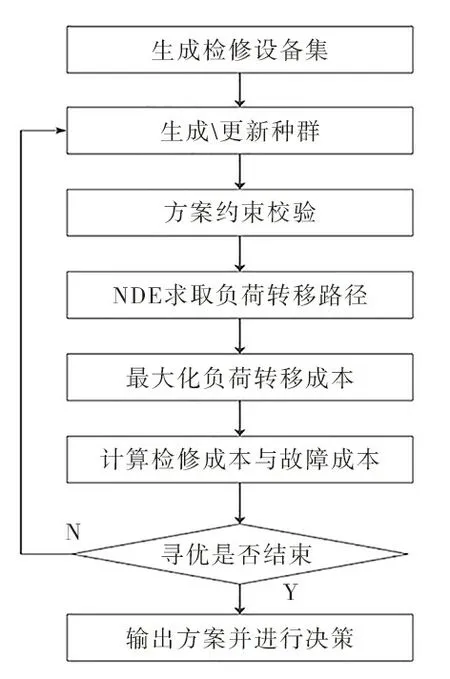
图1 基于遗传算法的求解流程示意

基于遗传算法进行模型的求解,根据确定的检修设备集确定算法种群规模和序列,生成初始种群,对种群进行约束条件校验,对于不满足约束条件的方案,赋予较大的惩罚因子。对于满足约束条件的方案,采用NDE的方法确定转移路径及失负荷成本,将成本反馈至检修方案构成检修方案的风险成本。对当代种群进行精英化保留与选择策略,更新当前种群进行下一代优化,直至优化程序结束,输出优化所得方案。

4 算例分析

4.1 基于IEEE33节点系统方法可行性算例分析

为了验证所提模型和算法的有效性,采用IEEE33节点系统进行仿真分析,见图2,分别在节点7和17接入容量为900 k W和450 k W的分布式电源,方差分别为期望的10%,设定一个检修周期为5周,每台设备检修耗时为1周,最大检修设备数为3。

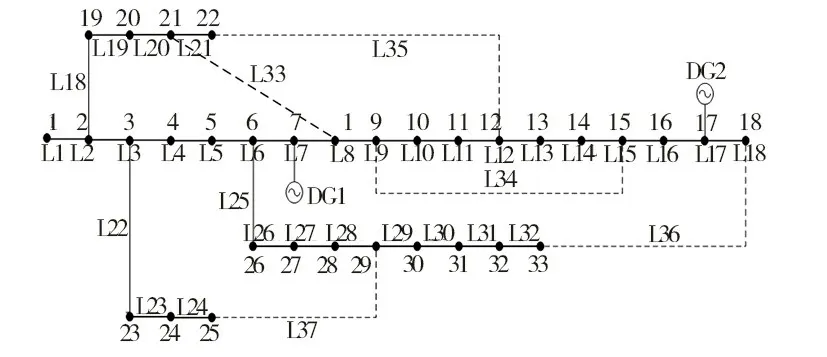
图2 IEEE 33节点配电系统

4.1.1 检修设备集的确定

根据设备状态监测的结果线路L8、L16状态评估得分为71分、66分,加入检修设备集。在该检修周期内对所有设备进行状态预测,预测结果较差的设备包括L15和L27,加入检修设备集。所以该检修周期的检修设备集包括L8、L15、L16、L27。

4.1.2 负荷转移方案的求取

根据2阶段负荷转移优化模型得到的结果,见表1。

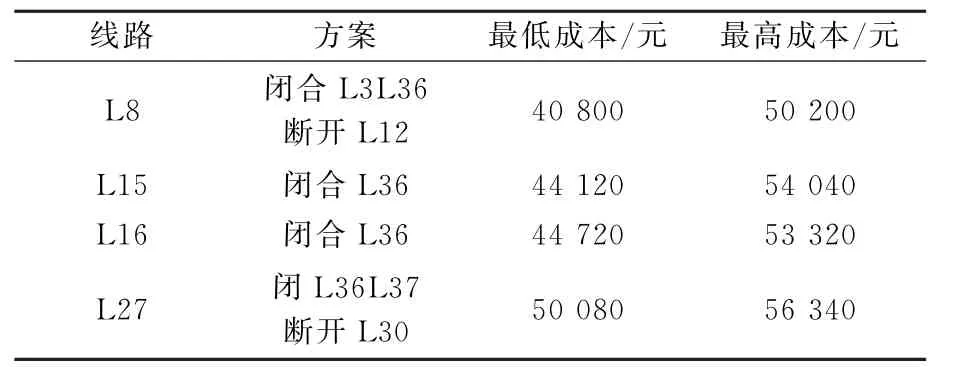
表1 检修方案对应负荷转移方案

通过特定工况下负荷转移方案的求取,得到的负荷转移方案真实可靠,能够满足检修计划制定过程中负荷转移优化的要求。并且通过2阶段中第2阶段计算对应最高成本,充分考虑了检修中面临的最大风险,使得负荷转移方案和后续检修方案的可靠性更高。

4.1.3 检修方案的求取

对所建模型进行求解,得到如下所示的Pareto关系曲线,见图3。由图3可看出,配电网检修风险与故障风险二者存在反向变化的关系,在图中每1个点都为1个方案,分别指向横纵坐标的该方案对应的2个风险指标。

图3 遗传算法最优解帕累托分布曲线

设立2个目标的单目标满意程度下限为0.7。采用总体目标贴近度法求取使得总体目标贴近度最大的方案,见表2。

表2 单目标满意度0.7水平下检修方案的确定

方案对应的总体目标贴近度为0.483 6,2个目标各自的满意度为0.793 1和0.735 6。对应方案的检修风险为32.12万元,故障风险为128.05万元,总风险为160.16万元。上述方案中,监测状态较差的设备L8和L16安排在前2周进行周检修,较早检修能够减小对系统的影响。设备L27与L15则被安排在同一周进行检修,通过负荷转移路径优化的结果可以发现,二者安排在同一时间能够保证系统可靠性运行,不会造成不必要的失电行为,因此是可行的。

4.2 基于RBTS Bus2系统的对比算例

以RBTS Bus2配电系统为例进行对比仿真分析(见图4)。在LP20接入风机DG1,在LP6接入风机DG2,容量都为0.7 MW,方差为期望的10%。

为分析所采用的检修模式与传统年度检修模式的差别,选择文献[8]中所安排检修的设备考虑检修,其余设备则认为状态良好。以设备预测状态对应的故障率为依据,进行抽样,模拟设备在线检测结果异常的设备情况。通过抽样得到的12个检修周期内在线监测结果处于异常情况的设备,见表3。

图4 RBTS Bus2配电系统

表3 模拟监测异常设备情况

连续进行12期的检修计划优化,得到该系统全年的检修计划,见表4。其中方案I为本文方法所得方案,方案II为文献[8]的方案。

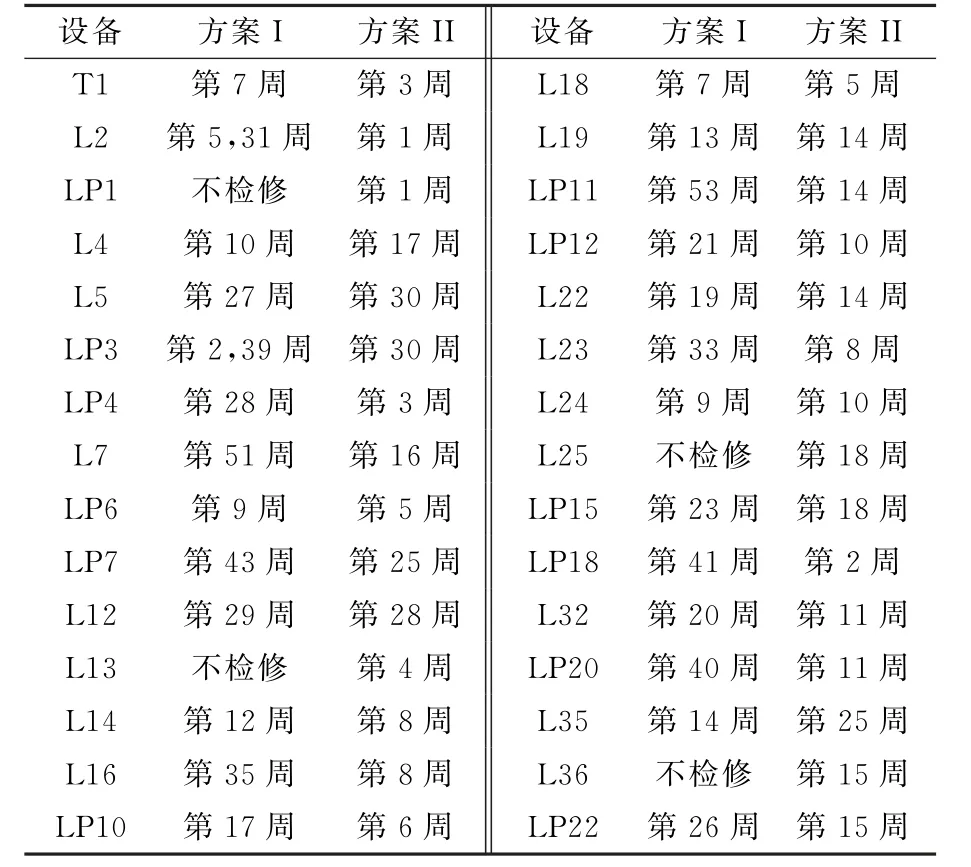
表4 2方案检修时间安排对比

对比上述2种方法,得出以下结论。

a.方案I考虑了设备在线监测的结果。通过以故障率为依据进行状态监测结果的模拟,进而对实际工作中具有随机性的设备实时状态进行仿真,具有处理状态检修实时性要求的优势,而方案II不能够处理状态检修的实时性。

b.方案I对部分设备安排了多次检修,而对另一部分设备没有安排检修,从而实现了不同检修周期内差异化的检修方案,形成了动态检修的机制。方案II以确定的方法在每一个检修周期内安排相同的设备检修,没有实现状态检修动态性的要求。

c.方案I由于存在检修设备集的考虑,所以能够合理地分布设备的检修时间,能够在全年时间内较为均匀地安排检修,而方案II处于可靠性与经济性的考虑,设备检修时间较为集中,前期检修设备过多,后期没有安排检修工作。

d.方案I与方案II在一些设备的检修时间上是相差不多的,原因在于二者均以设备的预测状态为依据制定检修计划,对于状态较差的设备能够较早地安排检修。

5 结束语

以设备状态监测和设备状态预测为依据构建检修设备集,最大程度地实现状态检修的要求。之后构建了以恢复成本最小为目标的负荷转移模型和以配电网检修风险和故障风险最小为目标的检修时间优化,对双层优化进行求解决策得到最优的方案,检修方案能够较好地适应电力企业的工作需要,具有一定实际意义。