隧道环境下频率域声波全波形反演优化方法对比
于明羽,吴遵红,谭 凯,彭代诚,熊绚兮,刘江平
(1.中国地质大学 地球内部多尺度成像湖北省重点实验室,湖北 武汉 430074;2.湖北特种设备检验检测研究院,湖北 武汉 430074;3.中国冶金地质总局 中南地质调查院,湖北 武汉 430081;4.中国地质大学 地球物理空间与信息学院,湖北 武汉 430074)
1 引 言
隧道工程是复杂地质地形区域交通基础设施建设最优选方案。隧道施工环境围岩地质情况复杂多变,经常会因遇到岩溶、断裂破碎带等不良地质体,造成塌方、突水等各种地质灾害,因此准确预报掌子面前方地质情况,避免突发隧道地质灾害损失,已经成为国内外隧道工程界关注的问题[1,2]。隧道超前探测方法,是一种全空间条件下在掌子面或迎头后方布置观测系统超前探测前方隐伏地质灾害的地球物理技术,目前隧道施工中多采用地球物理超前预报方法进行掌子面前方地质预报,其中,地震波法隧道超前探测方法以不良地质体与围岩的波速差异为基础进行隧道地质超前预报,具有较长的探测距离及较好的地质结构识别效果,是隧道内常用的超前探测地球物理方法之一[3-5]。但由于隧道地震方法超前预报观测系统受隧道环境限制,采集数据量无法满足对隧道地质体波速计算精度的高要求,超前预报数据处理成像结果对异常体分辨能力,无法达到对不良地质体精细探测的需求,只适用于简单地质情况[6],因此亟需适用于隧道超前地质预报的精细探测手段来改变这一现状。
全波形反演在地震勘探领域的发展,为研究者们提供了新的思路。全波形反演方法是一种基于全波场信息实现介质参数反演的高分辨率成像方法,20世纪80年代Tarantola和Lailly将时间域全波形反演的理念引入至地震勘探领域[7,8],相比常规利用单一反射波或初至波数据信息的处理方法进行物性参数反演成像,全波形反演充分使用了全波场的信息,达到了高精度、高分辨率的反演成像效果,因而备受推崇。全波形反演由于非线性和周期跳跃现象,导致目标函数存在多极值,使得反演对初始模型有严重依赖性,为此早期研究者们提出了对地震数据依次滤波的时间域多尺度全波形反演方法[9]来降低反演结果对初始模型的依赖。20世纪90年代,Pratt等将全波形反演的理论扩展到频率域,称为频率域全波形反演方法,频率域全波形反演中低频成分的反演结果可以直接作为高频成分的初始模型直接达到多尺度反演的效果,降低对初始模型的依赖性,这一优势使得频率域全波形反演在地震勘探领域的研究广泛发展[10,11]。
因此近年来越来越多研究者开始尝试将全波形反演的方法应用于隧道空间,包括地质雷达的隧道全波形反演、地震方法的隧道前方岩体速度反演以及隧道内部破碎位置的全波形反演[12-14]。考虑到近年来数学方法与地球探测理论的结合以及计算机技术的发展,更多最优化方法被应用于全波形反演的目标函数极值求取中,以期得到更精确高效的反演结果,从早期Tarantola等研究者们采用的梯度下降法,以及在Mora等讨论预条件处理策略的基础上,Santosa采用牛顿类方法全波形反演,而近来研究者们又将拟牛顿类方法应用到全波形反演中[15-17]。因此将全波形反演的方法应用于隧道空间不可避免地涉及到反演优化算法的选择,鉴于本文将目前几类常用方法中具有代表性的最速下降法、截断牛顿法以及l-BFGS方法应用到隧道环境下的频率域声波全波形反演,并对比不同方法的反演迭代收敛速率、反演效果以及时间消耗,以期达到为后续研究者们提供合理建议的目的。
2 频率域全波形反演原理及方法
2.1 频率域全波形正演及目标函数
二维频率域声波波动方程公式如下[18]:
=-s(x,z,ω)
(1)
式(1)中:k(x,z)为体变模量,ρ(x,z)为密度,d(x,z,ω)和s(x,z,ω)分别为波场压力函数与震源函数,(x,z)为空间位置向量,Δ为拉普拉斯算子。
波场压力函数d(x,z,ω)与震源函数s(x,z,ω)的关系是线性的,因此离散化的二维声波方程等式可以简化为如下的大型稀疏线性方程组:
A(ω)•d(x,z,ω)=s(x,z,ω)
(2)
式(2)中:d是波场矩阵,s为震源矩阵,A是关于频率和介质属性的阻抗矩阵,模型空间网格数为(Nx,Nz),d和s均表示(Nx,Nz)的向量,那么A(ω)是一个(Nx,Nz)×(Nx,Nz)的有限差分算子矩阵,可采用LU分解法对其进行求解[19]。
频率域全波形反演的目标函数选择为观测波场与计算波场差值的最小二范数,具体表示为:
(3)
式(3)中:f(d)表示波场残差的最小二范数,Δd表示观测波场与计算波场之间的波场残差,Nω表示反演频率个数,Ns表示震源个数,Nr表示接收点个数,dobs(s,r,ω)为实际观测值,dcal(s,r,ω)为计算波场。
2.2 频率域全波形反演优化方法
反演过程即是目标函数梯度寻优过程,由于全波形反演问题的高度非线性,一般采用逐步线性化的方法来减小地震记录和模型参数之间的非线性关系[20]。在全波形反演求解极小化目标函数的优化迭代中,对目标函数使用局部最优化算法求取极值,进行目标函数梯度、二阶导数等信息寻优来解决非线性极小化问题。目标函数梯度寻优中多采用梯度类方法、拟牛顿类方法以及牛顿类等方法,常见的梯度类方法有最速下降法、非线性共轭梯度法;牛顿类方法主要包括牛顿法、高斯牛顿法和截断牛顿法;拟牛顿法则以DFP算法和l-BFGS为主要代表[21,22]。
全波形反演目标函数最优化的标准格式及给定初始模型x0模型情况下模型更新迭代如下:
mind∈Cf(d)dk+1=dk+αΔdk
(4)
式(4)中,C为模型的约束集合,α为迭代步长,Δdk即为下降方向。
梯度下降法是目前最为常用的局部最优化方法,梯度下降法以最速下降法(STD)为代表,采用当前位置负梯度方向作为搜索方向,该方向为当前位置的最快下降方向。最速下降法计算较为简单,即:
Δdk=-f(dk)
(5)
Δf(dk)为目标函数f(d)在dk处的梯度。
牛顿法通过构建目标函数对模型的二阶导数Hessian 矩阵或者Hessian矩阵与向量的乘积来实现牛顿方程的线性求解[23,24]。以截断牛顿法(TRN)为例:
H(dk)Δdk=-f(dk)
(6)
梯度f(dk)为目标函数f(d)在dk处的梯度,H(dk)为海森算子H(dk)=-2f(dk)。在数学算法上牛顿类方法为二阶收敛,梯度下降法属于一阶收敛,牛顿法需要在每次迭代中重新求取海森算子的逆,计算步骤比梯度类方法多。
拟牛顿类方法以l-BFGS为例,相比直接的梯度计算法,l-BFGS法通过相邻迭代次数的模型向量差和梯度向量差构建Hessian矩阵的逆,从而实现对梯度的预处理作用,本质思想是使用正定矩阵来近似Hessian矩阵的逆,简化运算[25,26]:
Δdk=-Qκf(dk)
(7)
3 不同反演优化方法在隧道全波形反演中的反演效果
3.1 隧道模型设计与反演参数选择
地震隧道超前探测方法是在隧道掌子面及边墙内布置激发孔,在孔内通过人工激发地震波向隧道围岩中传播,当围岩波阻抗发生变化时,一部分地震波会被反射回来,另一部分地震波将会继续向前传播,反射回的地震波由接收器接收并传回电脑主机形成地震波记录,处理后的记录可预报隧道掌子面前方的地质变化,为隧道施工提供可靠的地质资料[27]。为方便讨论反演结果及相关影响因素,本文设计图1所示的隧道异常体模型和U型观测系统,图1(a)为隧道地质模型,模型长200 m,宽 30 m, 掌子面宽12 m,网格步长1 m;根据实际条件,已开挖隧道空间填充空气,隧道围岩速度4 000 m/s, 在掌子面前方14 m,46 m,84 m深度分别设计三个半径为3 m的圆形低速异常体,速度3 500 m/s,隧道地质体内采用均匀密度。图1(b)为U型观测系统,包含掌子面和垂直于掌子面的已开挖侧边,具体的观测系统为:炮点从51~101 m,间距2 m,两侧边各25炮,掌子面5炮,共55炮;检波点从51~101 m,间距1 m,两侧共102道,掌子面检波点13道,共115道,每次放炮时全排列接收。
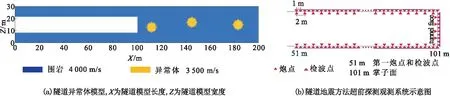
图1 隧道异常体模型及隧道观测系统示意图
全波形反演总体上是一个极小化目标函数的优化迭代求解过程,由于反演的非线性和周期跳跃现象,目标函数存在多极值,为了提高全波形反演对初值的稳健性,本文在隧道空间的全波形反演中采用频率域多尺度的反演方法(图2)。频率域多尺度反演方法先从低频出发开始反演,然后再逐级提高频率进行反演,由于对低频数据反演陷入局部极值导致不收敛的概率要小,因此可以采用低频反演结果得出相对较好的初始模型,以此提高反演过程的收敛。在进行隧道频率域声波全波形反演中,以异常体模型背景速度作为反演的初始速度模型,以图1(b)所示U型观测系统作为模型波场计算的观测系统,以200 Hz雷克子波为主频进行频率域正演模拟对隧道掌子面前方低速异常体模型进行频率域声波全波形反演。在多尺度全波形反演中,对垂直波数覆盖完成度越高的频率组,多尺度反演的效果就会越好,而垂直波数覆盖与最大偏移距相关,在隧道空间偏移距限制的情况下,隧道频率组无法完成垂直波数覆盖,因此多尺度的反演效果与频率组个数是正相关的关系[28],频率组内频率数量越多,反演效果越好。为对比不同反演优化算法,参考地震子波频谱范围设计[10 Hz,500 Hz]内自低频到高频频率组个数分别为15,18和21的三组频率(图2b),对每组频率分别进行三种不同反演优化方法下的隧道低速异常体模型频率域声波全波形反演,子波频谱和三个频率组选择如图2所示。

图2 隧道异常体正演子波频谱及全波形反演频率选择示意图
3.2 不同反演优化方法的反演结果对比
3.2.1 不同反演优化方法第一组频率反演结果对比
分别采用STD、TRN以及l-BFGS方法对相同初始模型进行图2(b)所示第一组频率的相同迭代次数隧道空间频率域声波全波形反演,经过依次对第一组频率的15个频率进行反演,最终三种反演优化方法分别得到如图3(c)~图3(e)所示的速度反演结果。

图3 隧道异常体反演模型及不同反演优化方法计算结果
可见经过由低至高的频率依次反演后,三种反演算法都可以得到隧道掌子面前方低速异常体的速度成像结果,表明全波形反演方法在隧道空间是可以得到速度成像的。图3(c)、图3(d)以及图3(e)反演成像结果表明,三类反演方法都能对异常地质体成像,对浅部异常体成像效果优于深部,随着深度加深,异常体成像效果变差,对浅部异常体反演结果的对比显示TRN以及l-BFGS方法的反演成像分辨率优于STD方法。为进一步对比三种反演优化方法的反演效果,绘制反演过程迭代收敛曲线以及过反演结果模型中线的速度剖面曲线如图4所示。

图4 三种反演方法迭代误差图及不同反演方法结果速度剖面对比
由图4(a)可见,不同方法反演的反演迭代收敛过程并非始终最速收敛,存在均方根误差值的局部跳动,参考反演过程中可能存在陷入局部极值的情况,这一现象反映了反演过程中搜索方向与实际误差最小值方向会存在一定差异,同时不同反演优化方法经过20次迭代后的误差值差异较小,其中l-BFGS反演算法相对收敛速度较快,经过20次迭代后误差值最小。由图4(b)可见,反演结果速度曲线中围岩范围速度出现起伏,异常体位置速度变化相对明显,同时TRN和l-BFGS反演算法得到的异常体速度值准确度高于STD反演算法结果。对反演结果剖面速度做速度平均,得到结果如图5。
STD、TRN和l-BFGS三种反演算法反演结果速度与真实模型速度相对误差分别为2.78 %,2.55 %,2.31 %,由图5可见三种反演方法得到的围岩平均速度误差较小,异常体的平均速度误差相对较大,其中l-BFGS反演算法速度结果最为接近真实模型速度,综合收敛速度分析可以得出l-BFGS方法在本模型的本次反演结果中表现最好。
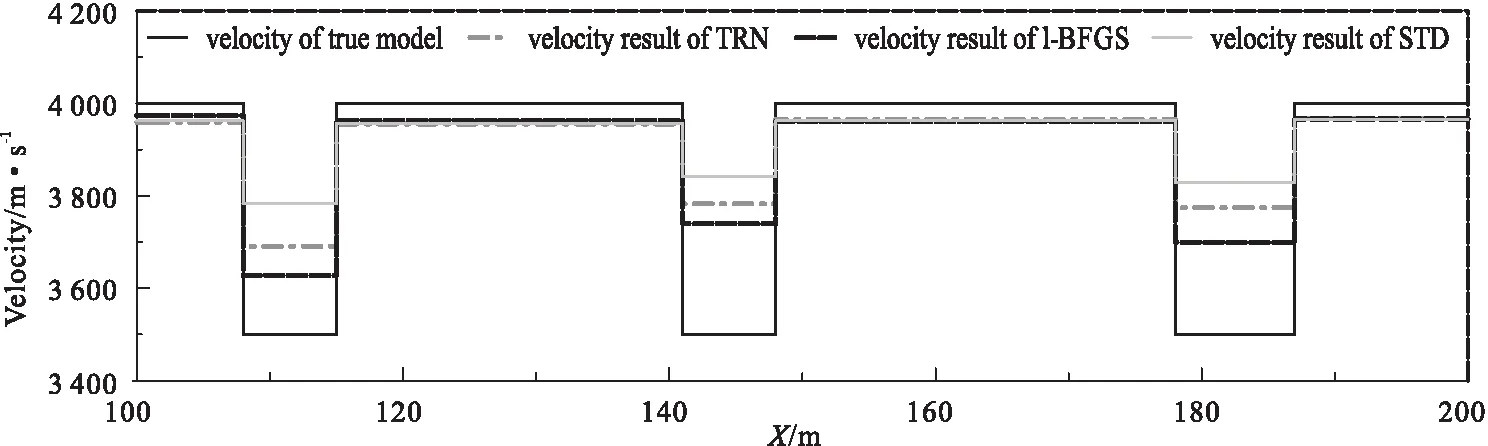
图5 三种不同方法反演结果平均速度剖面对比
3.2.2 不同反演优化方法第二组频率反演结果对比
分别采用STD、TRN以及l-BFGS方法对相同初始模型进行图2(b)第二组频率的相同迭代次数隧道空间频率域声波全波形反演,经过依次对第二组频率的18个频率进行反演,最终三种反演优化方法分别得到如图6(c)~图6(e)所示速度反演结果。

图6 隧道异常体反演模型及不同方法反演结果
对比第一组频率反演结果,可见第二组频率反演结果整体上浅部异常体成像分辨率变高,深部异常体成像效果也出现明显提高。由图6(c)、图6(d)以及图6(e)的反演成像结果可见,三类反演方法对异常体深度的位置反演都较为准确,在异常体位置与临近位置的围岩都有明显速度差异,随着深度加深,异常体成像效果变差,整体反演成像结果显示TRN以及l-BFGS方法的反演成像分辨率优于STD方法。为进一步对比三种反演优化方法的反演效果,绘制反演过程迭代收敛曲线以及过反演结果模型中线的速度剖面曲线见图7。

图7 三种反演方法迭代误差图及不同反演方法结果速度剖面对比
图7(a)对比可见TRN以及l-BFGS的收敛曲线相对收敛速度更快,TRN以及l-BFGS方法的最终结果模型的误差值小于STD方法的结果误差值,l-BFGS与TRN算法反演最终误差值近似。参考图7(b)剖面速度曲线对比可见,背景围岩速度存在起伏,异常体位置速度下降明显,同时TRN和l-BFGS反演算法结果值准确度高于STD反演算法结果。对反演结果剖面速度做速度平均得到结果如图8所示。

图8 三种不同方法反演结果平均速度剖面对比.
STD、TRN和l-BFGS三个反演算法反演结果速度与真实模型速度相对误差分别为2.45 %,2.27 %,2.23 %,TRN和l-BFGS方法的反演结果值差异不大,l-BFGS方法在本模型的本次反演结果中表现相对更好。
3.2.3 不同反演优化方法第三组频率反演结果对比
分别采用STD、TRN以及l-BFGS方法对相同初始模型进行图2(b)第三组频率的相同迭代次数隧道空间频率域声波全波形反演,经过依次对第三组频率的21个频率进行反演,最终三种反演优化方法分别得到如图9(c)~图9(e)所示的速度反演结果。
可见随着频率组个数的增加,隧道环境频率域声波全波形反演方法得到了隧道前方地质体较高分辨率的速度成像结果,体现了隧道环境下全波形反演方法高分辨率成像的优势。由图9(c)、图9(d)以及图9(e)的反演成像结果可见,三类反演方法对异常体深度的位置反演都较为准确,在异常体位置速度与围岩速度有明显差异,且TRN和l-BFGS优化反演算法成像结果分辨率相比STD明显更高。为进一步对比三种反演优化方法的反演效果,绘制反演过程迭代收敛曲线以及过反演结果模型中线的速度剖面曲线见图8。

图9 隧道异常体反演模型及不同方法反演结果
经过对比反演迭代收敛曲线图10(a)可见,STD方法收敛曲线跳动较为明显,TRN以及l-BFGS的收敛曲线相对收敛速度更快,TRN以及l-BFGS反演算法最终结果模型的误差值小于STD方法结果误差值,l-BFGS与TRN算法反演最终误差值近似,但收敛速度相对较快。参考图10(b)过掌子面中线的速度剖面对比可见结果背景围岩速度存在波动,反演速度在异常体位置准确下降,模型浅部的反演结果精度高于深部,同时TRN和l-BFGS优化反演算法反演得到的速度结果值准确度高于STD优化反演算法。对反演结果剖面速度做速度平均得到的结果如图11所示。

图10 三种反演方法迭代误差图及不同反演方法结果速度剖面对比

图11 三种不同方法反演结果平均速度剖面对比
STD、TRN和l-BFGS优化反演算法反演得到的速度反演结果相对误差值分别为2.25 %,2.07 %,2.01 %,TRN和l-BFGS方法的反演结果值相差不大,l-BFGS方法在本模型的本次反演中相对反演精度更高。
3.2.4 不同反演优化方法相邻频率组反演结果对比
对于主频较高的频率域多尺度全波形反演,为达到较好的反演效果,通常会选择相对较多的频率组来满足波束覆盖率,本文三种不同频率组的反演对比也表明了同一反演算法下频率组个数多的反演效果相对较好。为进一步对比不同反演算法的效果,本文采用频率个数不同的不同反演算法进行对比,将第二组18个频率下采用STD反演算法得到的模型速度剖面结果与第一组15个频率下l-BFGS算法和TRN算法反演的模型速度剖面分别进行对比,结果见图12。

图12 第二组频率反演结果与第一组对比
对比图12(a)可见,第一组15个频率下l-BFGS算法反演得到的结果模型速度剖面对异常体的反演精度比第二组18个频率下采用STD反演算法得到的模型速度剖面高,这表明了l-BFGS算法反演可以在频率组频率个数较少的情况下得到好于STD反演算法在频率个数更多条件下的反演结果。图12(b)显示15个频率下TRN算法反演得到的结果模型速度剖面精度与第二组18个频率下采用STD反演算法得到的模型速度近似,图12的对比结果侧面表明了反演算法的选择对反演结果精度的影响,即在其他参数相同的情况下,l-BFGS算法和TRN算法以更少的频率个数进行反演比STD算法以更多的频率个数反演的反演结果表现更好。
将第三组21个频率下采用STD反演算法得到的模型速度剖面结果与第二组18个频率下l-BFGS算法和TRN算法反演的模型速度剖面分别进行对比,结果见图13。

图13 第三组频率反演结果与第二组对比
对比图13(a)可见,第二组18个频率下l-BFGS算法反演得到的结果模型速度剖面比第三组21个频率下采用STD算法得到的模型速度剖面结果反演精度更高,这表明了l-BFGS算法反演可以在频率组频率个数较少的情况下得到明显好于STD算法在频率个数更多条件下的反演结果。图13(b)显示18个频率下TRN算法反演得到的结果模型速度剖面与第三组21个频率下采用STD反演算法得到的模型剖面速度误差更小,这一对比进一步验证了在其他参数相同的情况下,采用l-BFGS算法和TRN算法以更少的频率个数进行反演可以得到比STD算法更多频率个数反演情况下的分辨率更高的速度反演结果。
通过对不同频率组进行隧道空间频率域声波全波形反演三种优化算法的结果对比,综合可得二阶收敛的牛顿类方法TRN和拟牛顿类方法l-BFGS在隧道声波频率域全波形反演中得到的速度结果值准确度明显高于梯度类下降法的STD,同时TRN和l-BFGS优化反演算法的隧道声波频率域全波形反演结果精度近似,l-BFGS优化反演方法得到的反演结果精度相对更高;在反演迭代误差收敛过程中TRN以及l-BFGS方法的最终结果模型的误差值小于STD方法的结果误差值,l-BFGS优化反演算法的最终结果模型误差值与TRN方法最终误差值近似,但l-BFGS优化反演算法的收敛速度更快。
3.3 不同反演优化方法的并行运算消耗对比
不同于常规地震波形反演方法只需要单一波形的数据存储,全波形反演需要存储数量较多的不同时刻正向传播波场快照,此外二阶计算的截断牛顿法还需要另外存储反向传播的波场快照,这些均涉及到大量内存开销,因此全波形反演方法的波场模拟和反演对内存的需求导致利用单个进程计算已变得越来越困难[29,30]。随着计算机技术的发展,MPI并行编程技术(分布式内存多线程同时工作)逐渐在全波形反演中应用开来,这一方法的使用,极大地提高了计算效率,减少了计算时间,使得全波形反演向多维及大数据量的应用研究发展成为可能[31,32]。本文在进行基于隧道空间频率域声波全波形反演的反演优化方法对比时,将MPI并行全波形反演算法应用于全波形反演的正演波场计算和反演梯度计算过程中,采用四线进程同时工作的方式完成了三种不同反演方法的隧道空间全波形反演计算。包含有并行算法的基于隧道空间频率域声波全波形反演计算流程见图14。
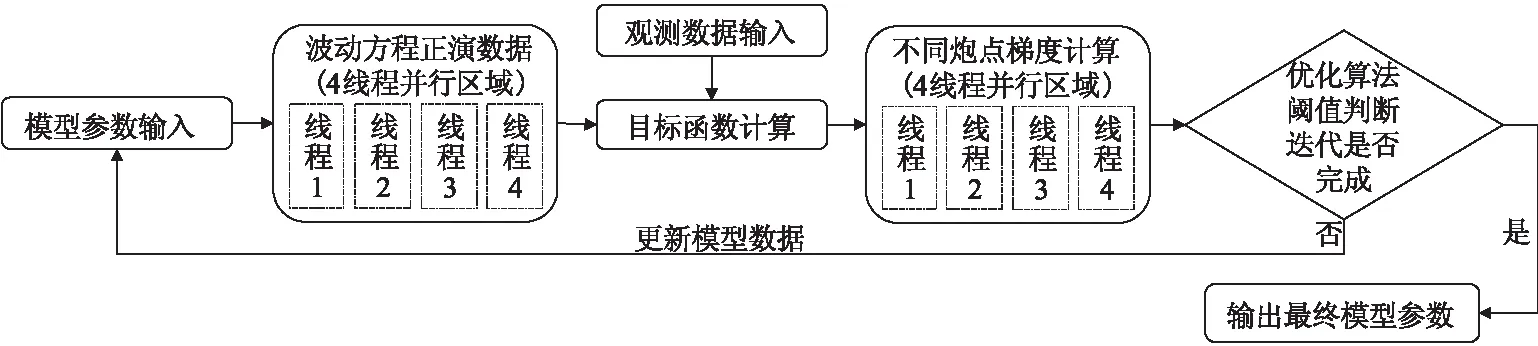
图14 基于并行算法的隧道空间频率域声波全波形反演流程
在相同内存条件下对相同的模型和数据采用三组频率进行反演,分别对三种优化算法程序计算时长对比,计算过程中STD、TRN以及l-BFGS方法反演程序计算总时长具体对比曲线见图15。

图15 三种反演方法并行计算耗时以及计算总耗时对比
其中TRN优化反演算法的计算时长最长,体现了二阶算法在计算和存储方面的更多消耗,其次是l-BFGS算法,l-BFGS算法的计算时长相比TRN明显减少,三组频率计算时长平均只相当于TRN算法消耗时长的61.2 %,而STD算法的计算时长最小,平均只相当于TRN算法消耗时长的43.6 %。相同内存下计算时长的对比表明TRN优化反演算法的计算时长最长,l-BFGS算法的计算时长相比TRN明显减少,而STD算法的计算时长最小,节约了超过一半的时间。
4 结论与建议
本文通过将分属于梯度类反演方法、牛顿类反演方法以及拟牛顿类反演方法的三种不同优化方法应用于隧道环境下的二维频率域声波全波形反演,对比反演效果、反演过程的迭代收敛速度以及反演过程中的时间消耗得出如下结论:
1)经过对隧道超前探测地震观测系统下的低速异常体隧道模型进行三种不同优化反演方法的频率域声波全波形反演,在频率组选择合适情况下三种方法均可得到隧道前方地质体的速度成像结果,证明了隧道环境下全波形反演方法是可行的,同时三类反演方法都对异常体位置较敏感,反演结果显示异常体位置速度与围岩速度有明显差异。对比可见TRN方法和l-BFGS方法反演结果成像分辨率明显高于STD,采用TRN和l-BFGS优化反演算法可以在频率数量较少的情况下得到与STD反演算法较多频率个数反演相近的结果,佐证了反演算法的选择对反演结果的影响。
2)在隧道异常体反演迭代收敛过程中可见,TRN和l-BFGS方法比STD方法具有更快的收敛速度,同时可以得到更小的最终误差结果,在相同的反演迭代次数中TRN和l-BFGS方法表现更为优秀,l-BFGS方法的最终结果模型的误差值与TRN方法最终误差值近似,但l-BFGS方法收敛速度更快。
3)相同内存下计算时长的对比表明TRN优化反演算法的计算时长最长,l-BFGS算法的计算时长次之,STD算法的计算时长最小,可见二阶算法时间消耗更大。同时l-BFGS算法的计算时长比TRN明显减少,只相当于TRN算法消耗时长的61.2 %,而STD算法的计算时长只相当于TRN算法消耗时长的43.6 %,节约了超过一半的时间。
本文综合反演结果的准确程度以及反演迭代过程中的收敛速度和成像精度,在相同的初始模型和计算参数下,得出l-BFGS优化反演算法表现更好,TRN算法其次,但STD算法和l-BFGS算法相比TRN算法具有较为优越的计算速度,基于全波形反演巨大的计算消耗和内存需求,以及隧道超前探测的高分辨率成像效果需求,本文建议使用l-BFGS优化反演算法来进行隧道空间的频率域全波形反演,希望这一结论可为隧道空间的全波形反演后续研究和发展提供借鉴。
致 谢
感谢对本文做出贡献的Seiscope课题组开发的全波形反演算法以及对本文提出宝贵意见的课题组成员们。

