基于强化学习的煤矸石分拣机械臂智能控制算法研究

张永超， 于智伟， 丁丽林

(山东科技大学 机械电子工程学院，山东 青岛 266590)

0 引言

煤矸石分拣是煤炭粗选的首要环节，也是提高煤炭质量以及矿井效益的重要方法[1]。传统煤矸石分拣如人工分拣、湿选和干选等分拣方式正面临工伤风险率高、环境污染严重及智能化程度低的困境[2-3]。而机械臂分拣不仅能有效降低工伤风险率，同时还具有效率高、绿色分拣的优势。《关于加快煤矿智能化发展的指导意见》也明确提出对具备条件的煤矿要加快智能化改造，推进危险岗位的机器人作业，到2035年各类煤矿基本实现智能化，建成智能感知、智能决策、自动执行的煤矿智能化体系。煤矸石分拣朝着智能机器人化方向发展符合现代工业发展趋势。

目前，用于机器人分拣机械臂的控制算法主要有抓取函数法[4]、基于费拉里法的动态目标抓取算法[5]、金字塔形寻优算法[6]、比例导引法[7]等。这些控制算法中除抓取函数法仅适用静态目标外，其他控制算法均可在已获取目标位置的前提下，实现快速接近目标的目的。然而将以上控制算法应用于煤矸石分拣机械臂时发现，煤矸石分拣机械臂的工作效率严重受限于控制算法中机械臂运动学或动力学等环境模型的设计精度，若精度低则会使煤矸石分拣机械臂末端执行器不能良好接近目标，造成较高的漏选率[8]。王鹏等[9]设计了一种基于机器视觉技术的多机械臂煤矸石分拣机器人系统,该系统可高效分拣50～260 mm粒度的煤矸石，并且能良好适应不同带速，但其机械臂控制算法仍依赖模型的精确性。因此，研究一种可使煤矸石分选机械臂稳定高效运行的无模型智能控制算法对实现煤矸石分选作业无人化、智能化具有重要意义。

强化学习作为一种重要的机器学习方法，因其控制过程不依赖于精确环境模型的特点，在机器人智能控制领域具有重要地位。它强调在与环境的交互中获取反映真实目标达成度的反馈信号，强调模型的试错学习和序列决策行为的动态和长期效应。深度确定性策略梯度(Deep Deterministic Policy Gradient，DDPG)算法是强化学习中常用来处理具有连续性动作空间任务的一种优秀控制算法[10]，但传统DDPG算法的奖励函数仅是基于欧几里得距离设计的，缺乏动作惩罚项等约束项，训练过程中容易使机械臂学习到输出较大关节角控制量的策略。若奖励函数设计不合理,还会出现稀疏奖励问题，使机械臂学不到期望的策略[11]。

针对以上问题，本文提出了一种基于强化学习的改进DDPG算法，并用于煤矸石分拣机械臂的控制。通过设计奖励函数使机械臂能更快学习到平稳接近目标的策略。通过改进Actor和Critic神经网络结构以及使用批标准化和Dropout优化方法，使算法具有更稳健处理机械臂关节角等低维输入观测值的能力[12]。仿真实验结果表明，改进的DDPG算法与传统控制算法相比具有无模型通用性强及在与环境交互中可自适应学习抓取姿态的优势，并且学习能力优于传统DDPG算法，其在大型连续动作空间具有巨大的潜在应用价值。

1 DDPG算法

DDPG算法属于Actor-Critic算法，它在确定性策略梯度(Deterministic Policy Gradient，DPG)算法[13]的基础上融入了深度神经网络[14]。DDPG算法的参数更新思想借鉴了深度Q网络(Deep Q Network，DQN)算法中的双网络延时更新和经验回放机制来切断数据相关性，训练过程中使用批量标准化[15]来提高学习效率。

DDPG算法中的Actor策略网络可在连续动作空间进行探索以及做出动作决策，Critic价值网络则负责评判决策优劣，以此指引Actor策略网络参数更新。两者均包含2个具有相同结构的神经网络，即目标网络和估计网络。Actor的估计网络是根据Critic的估计网络的指引实时更新，Critic的估计网络是根据自身目标网络的指引实时更新，因此，估计网络的参数是最新参数，而目标网络参数则是根据估计网络参数使用滑动平均方式来延迟更新的，Critic的估计网络参数的更新方式为最小化均方误差L：

(1)

式中：N为从经验池中取出的数据总个数；yi为i时刻目标Q值的更好估计；Q(si,ai|θQ)为估计Q值；si为i时刻的环境状态；ai为i时刻的输入动作；θQ为Critic网络中估计网络的参数，Q代表Critic网络中的估计网络；ri为i时刻的即时奖励；γ为折扣率；Q′(si+1,μ′(si+1|θμ′)|θQ′)为目标Q值；μ′(si+1|θμ′)为确定性策略,μ′为Actor网络中的目标网络,θμ′为Actor网络中目标网络的参数；θQ′为Critic网络中目标网络的参数,Q′为Critic网络中的目标网络。

这种利用估计网络和目标网络进行参数更新的双网络机制切断了数据相关性，有效提高了算法收敛性。类似于监督学习标签的yi为Critic估计网络参数的更新指明了方向，使参数更新更稳定。

Actor策略网络基于策略梯度更新网络参数：

θμJ(θμ)≈

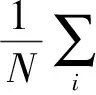
(2)

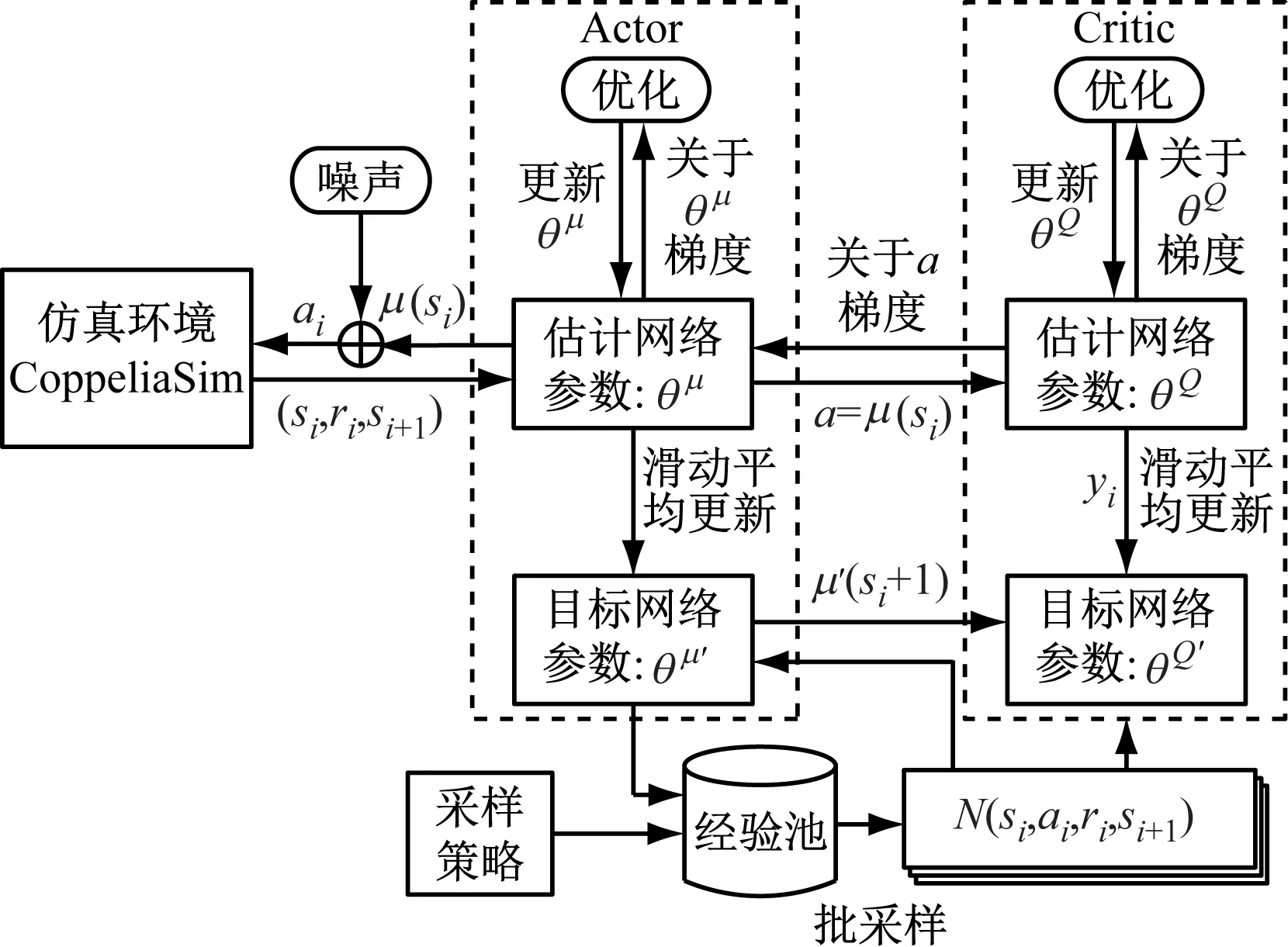
图1 DDPG算法结构

2 改进DDPG算法

2.1 神经网络结构

改进DDPG算法应用对象为六自由度煤矸石分拣机械臂，其动作空间庞大且应用环境复杂，为使神经网络更容易学习其输入特征数据的分布，同时也为缓解训练过程中神经网络的过拟合问题，Actor网络使用4层计算层并引入批量标准化方法和Dropout方法，以使模型训练更稳健，Actor网络的双网络均采用图2所示的神经网络结构。

图2 Actor神经网络结构

Actor框架中的估计网络输入层接收环境实时状态si，目标网络输入层接收智能体与环境交互后的下一状态si+1。批量标准化(Batch Normalization,BN)层通过减小数据在神经网络层传递过程中数据分布的改变，使神经网络参数更新更快且更易学习到知识，又因其是在小批量样本上计算均值和方差，难免引入小噪声，这也同时提高了神经网络的泛化能力。隐藏层中层1和层2中的黄色神经元表示该层使用了Dropout方法，Dropout方法通过使部分神经元随机失活以减小神经元之间的依赖性，促使神经网络学习更稳健的特征，提高了网络的鲁棒性。

Critic网络的估计网络和目标网络采用如图3所示的3层全连接神经网络来拟合Q(si,ai|θQ)和Q′(si+1,μ′(si+1|θμ′)|θQ′)，并使用BN层和Dropout方法缓解神经网络过拟合，从而使Critic网络可更好评判Actor网络输出动作的优劣。

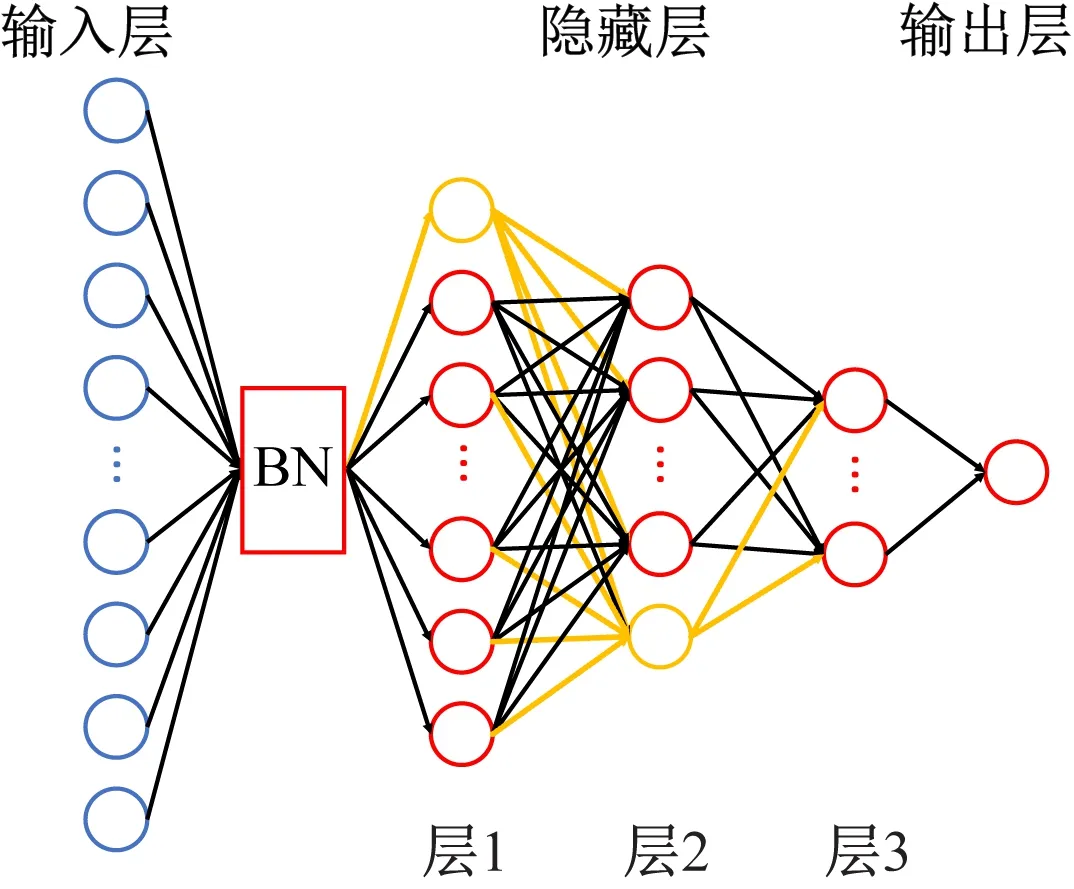
图3 Critic神经网络结构

2.2 奖励函数设计

为使煤矸石分拣机械臂可自适应学习到接近目标的方法，同时解决传统机械臂强化学习控制方法输出动作过大以及稀疏奖励容易被淹没的问题，本文在传统DDPG算法的基础上设计了可持续输出收益的奖励函数：

(3)

终止状态判定项通过给可输出连续跟踪目标动作的智能体一个较大的奖励值来诱导机械臂学习到跟踪目标的能力，减小目标与机械臂末端执行器的冲击。

3 煤矸石分拣机械臂智能控制原理

改进DDPG算法依据马尔科夫决策过程[16]控制机械臂在与环境交互中学习知识，任务是找到能最大化智能体期望回报的最优策略[17]，即最大化估计Q值。在煤矸石分拣机械臂控制任务中，强化学习中的智能体为具有决策能力的煤矸石分拣机械臂。估计Q值的更新依据自身梯度以及其与目标Q值q的均方误差来指引，其中q为

q=ri+γQ′(si+1,μ′(si+1|θμ′)|θQ′)

(4)

机械臂根据相应传感器返回的煤矸石位置以及机械臂状态进行决策，输出机械臂预测控制量，并根据机械臂执行动作之后的环境状态如末端执行器与煤矸石的距离、机械臂的位置、煤矸石的位置等进行下一步决策。通过不断试错学习，使网络参数向可输出机械臂探索过程中所遇最大q值方向更新，直到机械臂可以根据环境状态准确输出接近煤矸石的策略或幕奖励波动趋于稳定时即可提前终止训练。煤矸石分拣机械臂控制流程如图4所示。首先初始化改进DDPG算法权重，然后加载训练权重，最后根据煤矸石位置及关节角状态输出相应的关节角来控制机械臂运动，以使末端执行器接近煤矸石。煤矸石位置以及机械臂关节角状态由相应检测模块和传感器测得。

图4 机械臂控制流程

4 实验及结果分析

4.1 环境配置

本文采用CoppeliaSim搭建虚拟环境模型，并在环境模型中创建UR5机械臂、RG2执行器、输送带、煤和煤矸石，以此模拟实际煤矸石分拣环境，仿真平台如图5所示。

图5 仿真平台

使用Python在tensorflow2.2.0上编写改进DDPG算法框架，并调用CoppeliaSim创建的虚拟环境来训练算法。算法中Actor的双网络和Critic的双网络神经元配置见表1，其神经网络输入状态si为6个关节角度、执行器指定点的绝对坐标、第5个关节的绝对坐标、末端执行器指定点与煤矸石中心的距离。奖励函数参数c1和c2经测试设定为0.1和0.2，使用30倍的高斯分布噪声，设定算法循环幕数为5 000，每幕迭代步数为300，若末端执行器中设定的特定点与煤矸石中心距离为0时，超参数b被赋值为10，若下一步距离仍为0，则b继续累加10，当其累加了20步时，即跟踪了20步，则提前结束当前幕。

表1 Actor和Critic神经网络中各层神经元数量

4.2 性能对比测试

为测试改进DDPG算法的性能，将其与仅使用欧几里得距离作为奖励函数的传统DDPG算法在相同环境下进行训练对比，经5 000幕迭代后，改进DDPG算法每幕奖励结果如图6所示，传统DDPG算法每幕奖励结果如图7所示。

图6 改进DDPG算法每幕奖励

强化学习不同于传统监督学习，其训练样本没有确定标签，也就没有真正意义上的损失函数，因此，当幕奖励趋于稳定时，即可认为机械臂在当前环境中学习到了基于所用算法的最优策略。由图6和图7可看出,改进DDPG算法和传统DDPG算法指引下的机械臂在环境中经过随机探索后都学习到了一种策略，改进DDPG算法训练稳定后的每幕奖励接近机械臂探索过程中的最大值，而传统DDPG算法训练稳定后的每幕奖励与机械臂探索过程中遇到的最大奖励相差较大，这表示所设计的奖励函数比传统奖励函数更具有诱导机械臂学习到最优策略的能力。

图7 传统DDPG算法每幕奖励

为了进一步测试2种算法训练后的性能，将训练后的改进DDPG算法和传统DDPG算法进行泛化能力对比验证，测试过程为在虚拟环境中继续添加红色、黄色、绿色物块，如图8所示，图中灰色物块为2种算法在学习过程中所用的训练目标，使用这4种颜色的物块代替实际分拣环境中的煤矸石，将这4种煤矸石分别设定为测试目标，并使用2种算法分别对其进行10次接近测试，结果见表2。

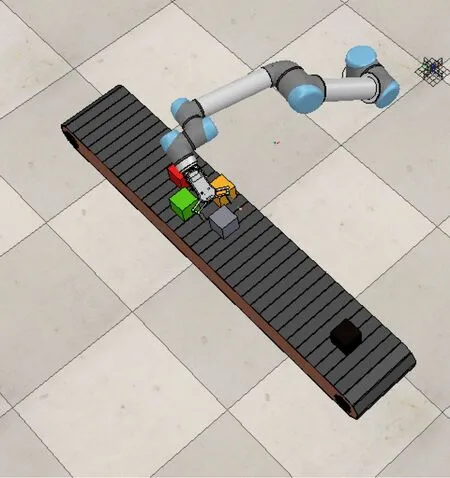
图8 CoppeliaSim虚拟环境

表2 测试结果

由表2可看出，改进DDPG算法具有良好的泛化能力，即接近训练过程中未曾出现过目标的能力，而传统DDPG算法泛化能力较差，这也进一步验证了改进DDPG算法控制下的机械臂所学策略质量较高。在接近测试过程中，传统DDPG算法控制下的煤矸石分拣机械臂的末端执行器多数以一种垂直于虚拟环境中地面的非常规姿态位于物块之上，这也证明了传统DDPG算法控制下的机械臂并未学习到良好的策略。在黄色物块接近测试中，传统DDPG算法控制下的煤矸石分拣机械臂末端执行器特定位置的运动轨迹如图9所示，改进DDPG算法控制下的末端执行器特定位置运动轨迹如图10所示。从图9和图10可看出，改进DDPG算法与传统DDPG算法相比，其控制策略可以更好地使末端执行器接近目标。

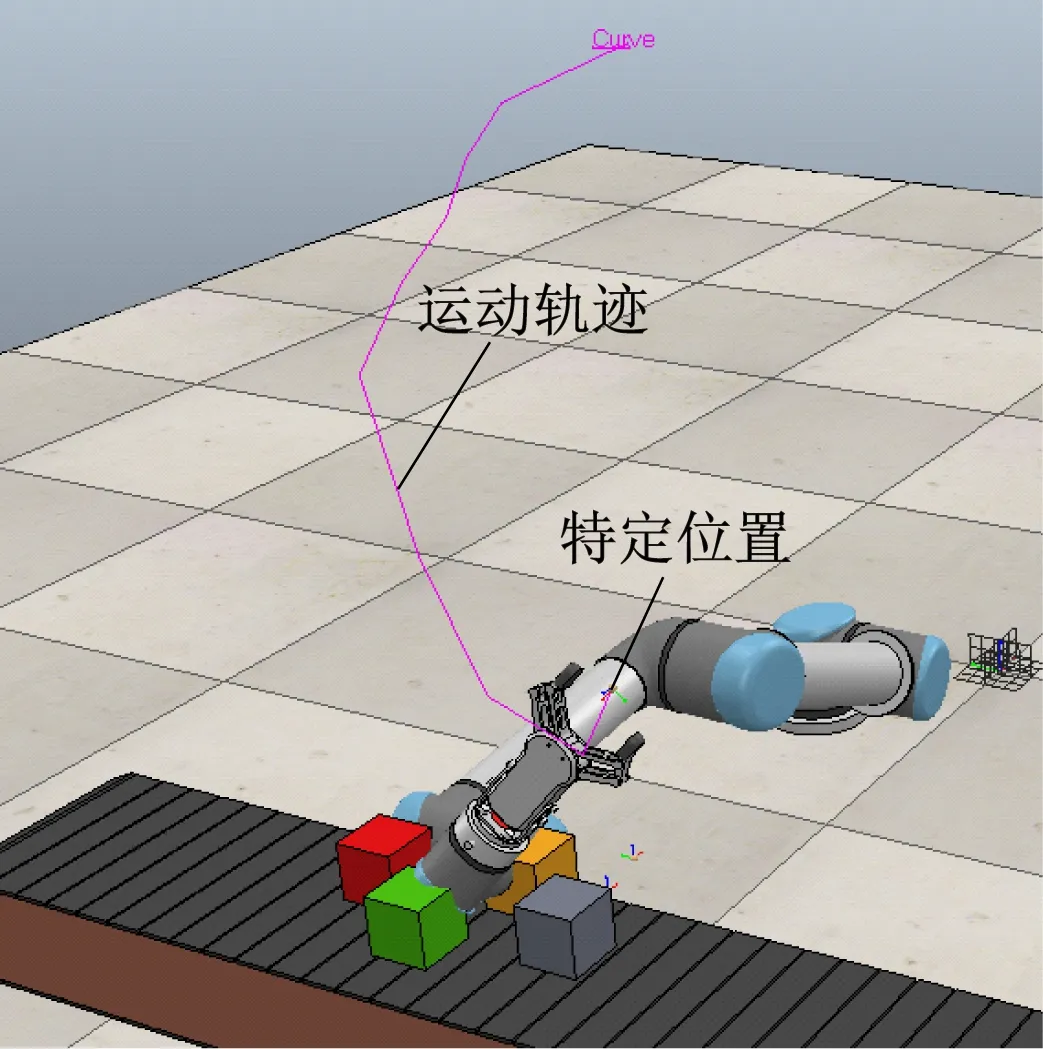
图9 传统DDPG算法控制结果

图10 改进DDPG算法控制结果

黄色物块接近测试中，2种算法输出的一次关节角控制量对比如图11所示。从图11可看出，改进DDPG算法因受奖励函数输出动作惩罚项的影响，其关节角输出控制量小于传统DDPG算法的输出，降低了因大幅度更新关节角对机械臂性能造成的影响。

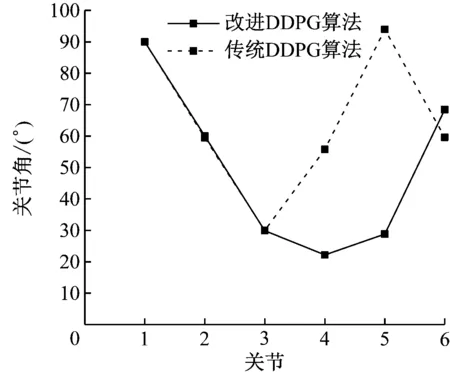
图11 2种算法输出的一次关节角控制量对比

综上可知，改进DDPG算法和传统DDPG算法控制下的煤矸石分拣机械臂通过与环境交互均可使机械臂学习到一种控制策略，但测试结果表明，传统DDPG算法所学策略性能较差，不能良好接近目标，改进DDPG算法所学策略更接近最优。

5 结论

(1)对传统DDPG算法中的神经网络结构和奖励函数进行了改进，提出了适合处理六自由度煤矸石分拣机械臂的改进DDPG算法。改进DDPG算法经过训练后，Actor网络即可根据环境状态映射成具有最大估计Q值的关节状态控制量，最终经相应运动控制器控制煤矸石分拣机械臂接近煤矸石，实现煤矸石分拣。

(2)实验结果表明，改进DDPG算法相较于传统DDPG算法可更快收敛于探索过程中所遇最大奖励值。改进DDPG算法可控制机械臂小幅度接近煤矸石，具有较强的泛化能力，为解决实际煤矸石机械臂智能分拣问题提供了一种新方法，同时也为后期与基于深度学习的视觉检测联合使用提供了理论保障。