基于WT-IPSO-BPNN的电力系统短期负荷预测

康 义 师刘俊 郭 刚

基于WT-IPSO-BPNN的电力系统短期负荷预测

康 义1,2师刘俊1郭 刚3

（1. 华北水利水电大学电力学院，郑州 450045； 2. 郑州上控电气技术有限公司，郑州 450001； 3. 国网河北省电力有限公司邯郸供电公司, 河北 邯郸 056000）

鉴于短期负荷预测精度对电力系统安全、经济和可靠运行的重要性，为提高预测精度，本文提出了基于小波分解（WT）、改进粒子群算法（IPSO）和BP神经网络的组合预测模型。首先运用小波分解对负荷数据预处理，将历史数据分解成cd1、cd2、cd3以及ca3；然后对分解后的小波序列分别进行神经网络建模和预测；最后小波重构负荷序列的最终预报。为提高BP神经网络所需样本的精确性和神经网络的收敛速度及稳定性，采用改进粒子群算法优化网络，形成了“分解-预测-重构”模型。经实例验证，与小波分解BP神经网络方法相比，本文所提方法具有训练学习能力更强、收敛速度更快、预测精度高和适应能力更强的优点。

小波分解；粒子群算法；BP神经网络；负荷预测

0 引言

电力系统短期负荷预测是针对一天到一周的电力负荷进行预测，主要应用于电力系统日常电网的调度，及时对网络区域内的电力使用进行管理分配；为调度机构制定发电、供电和需电平衡策略提供理论依据，是保证电网安全、稳定运行的关键，且还可以为水、火、核电配置提供指导，合理计划机组起停时间；同时在电力市场为发电侧提供电量分配研究依据，促进电网和发电侧参与市场竞争，提高电力行业经济效益和社会效益。所以提高负荷预测精度有利于电网的安全稳定运行和电力市场的合理竞价，降低电网运行风险[1-2]。

由于负荷预测受到如气象、时间、工业结构和社会因素等多方面非线性因素以及数学建模的影响，预测精确度很难得到保证。因此应综合考虑多种因素的影响，寻求新的、适应能力更强的负荷预测方法，以提高预测的准确性。文献[3]利用改进的神经网络模型进行预测。文献[4]建立了时钟频率和Spark平台驱动循环神经网络的预测方法。文献[5]提出了基于神经网络的负荷模型参数进行预测。文献[6]对小波神经网络的结构模型进行了改进，效果较好。文献[7]引入门控循环单元（gated recurrent unit, GRU）网络，处理具有时序性特点的历史负荷序列。电力负荷的变化错综复杂，单一的预测方法精度往往不高，因而目前综合各预测方法的优点、实现多种方法的组合预测得到了广泛的应用。文献[8]利用粒子群算法（particle swarm optimization, PSO）优化神经网络（neural network, NN）的权值和阈值，提高预测准确性。文献[9]结合受限玻尔兹曼机的递归神经网络的方法。文献[10]结合BP神经网络的正向和反向传播过程，建立基于Hadoop架构中Map Reduce框架的BP神经网络负荷预测模型。文献[11-12]提出粒子群算法优化神经网络的短期负荷预测方法。文献[13]采用灰色模型优化神经网络的方法。文献[14]结合长短期记忆（long short term memory, LSTM）和卷积神经网络（convolutional neural network, CNN）建立了混合预测方法。文献[15]用小波分解后的系数进行优化。文献[16]采用机器学习预测短期负荷。

本文提出基于小波分解、改进粒子群算法（improved PSO, IPSO）和BP神经网络的预测模型，利用小波分解对负荷数据进行预处理，分解成不同尺度上的序列进行分析选用相应的模型预测。采用改进粒子群算法，加强历史数据的规律性。通过阈值来减少系数的数量，增加信息的有效性。

1 小波变换

小波变换理论继承和发展了短时傅里叶变换局部化的思想，对电力系统负荷进行分解，得到具有不同周期特性和频次的子序列，针对子序列的具体情况，选择与之相适应的预测方法，使预测更有针对性。它的主要特点是通过变换能够充分突出问题某些方面的特征，能对时间（空间）频率的局部化分析，通过伸缩平移运算对信号（函数）逐步进行多尺度细化，最终达到高频处时间细分、低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节。

1.1 小波分解

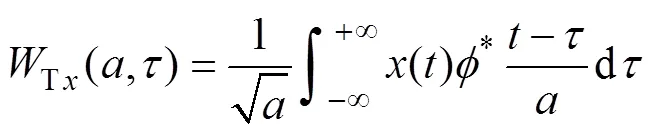
式中，＞0为尺度因子。

小波变换满足条件为

设()∈2()是采集的信号，标准正交基为0,n= {(-)}和0,n={(-)}，其中∈Z。

选定一种小波进行3层小波分解，Mallat分解算法为

利用小波对采集的数据进行多尺度分解，能加强历史数据变化的周期性，得到高低频信号，再根据具体情况确定合适的分解层数。

1.2 小波重构

小波重构是小波分解的逆变换，它是将分解后经过运算的数据信息还原到原始数据的过程。小波变换重构原始信号的逆变换为

当人体词的形貌、位置及功能特征向其他人体部位或具体的非人实体认知域映射时，根据概念隐喻的意象图式和相似性原则，我们可以容易地辨析出其隐喻意义，但也有一部分人体部位的特征是投射到抽象的概念域中，这时人体词就可能表示抽象事物、空间、时间、性质或程度等。此外，当人体词作为目标域概念，其他认知域特征向其映射时，人体词的语义也会发生转移。此时要想解读出准确的人体词语义就要费些周折。

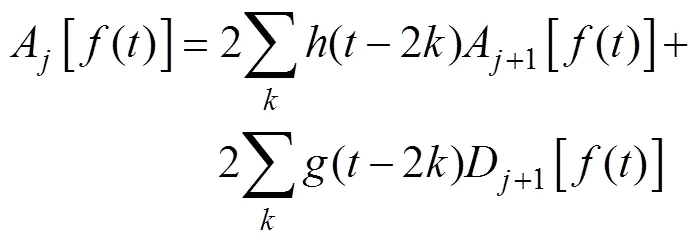
2 BP神经网络

标准BP神经网络由输入层、隐含层和输出层组成，如图1所示。其采用梯度搜索技术，按照误差反向传播训练，使网络的实际输出值和期望输出值的误差最小。

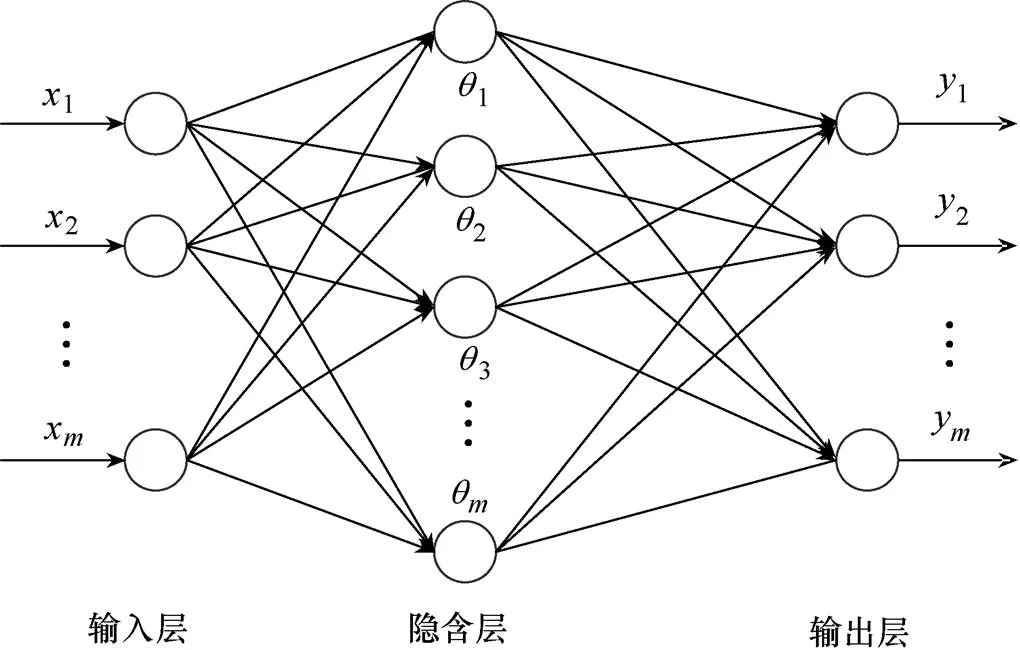
图1 BP神经网络结构

于是L-M法的调整公式为

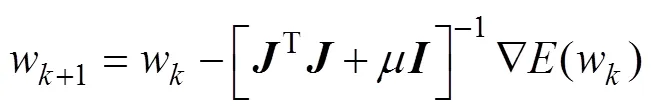
是根据训练程度调整的值，在最初开始训练时，取值很大，在这种情况下，就相当于梯度下降法；随着训练误差逐渐接近最小值即极小点附近时，逐渐减小至0，此时，网络的修正方向就完全是拟牛顿法的修正方向，拟牛顿法是寻求最佳的修正方向。因此，L-M法比其他方法都更高效。

3 改进粒子群算法

PSO算法是受到鸟类动物群体行为的启发，根据个体以及群体的信息，通过迭代，更新粒子的位置，并不断修正种群极值，动态地更新粒子的位置和速度，通过不断重复上述过程，实现最优解的寻找。由于传统粒子群算法容易产生早熟收敛和局部最优的问题，所以考虑从惯性权重和学习模式对算法进行改进[17]。传统粒子群算法的粒子速度与位置更新公式如下

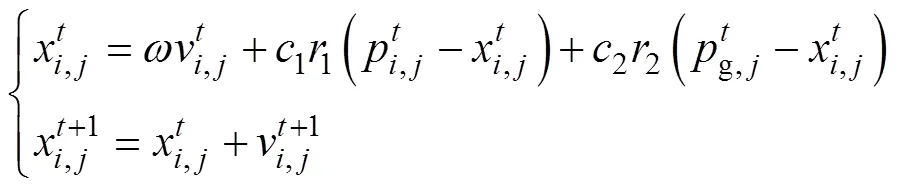
3.1 惯性权重的改进

权重系数在PSO的寻优过程中十分关键。权重系数小则PSO的局部搜索能力强，权重系数大则PSO的全局搜寻能力强。粒子群的收敛速度和寻优效果会受权重系数的影响，因此提升PSO的寻优能力和收敛速度可以通过选择合适的权重系数来实现。

在PSO中，惯性权重的改进形式如下

式中：max为算法最大迭代次数；为惯性权重；为当前迭代次数。

3.2 学习模式的改进

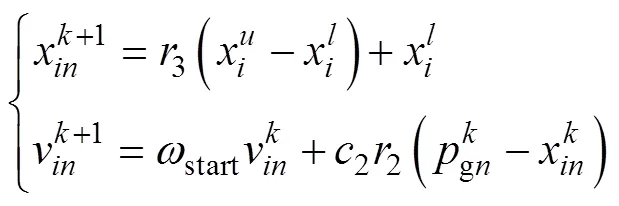
使用PSO来对网络的权值和阈值进行优化，使BP神经网络在初始阶段就拥有较优的初值，进而缩减了训练时间并提高了收敛精度。因此，对于PSO每一个粒子所携带的信息就是BP神经网络的所有权值和阈值。权值包括输入层与隐含层、隐含层与输出层之间的所有权值，阈值包括隐含层和输出层的各个神经元阈值。改进粒子群优化参数流程如图2所示。

4 小波粒子群优化神经网络模型建立

本文采用小波分解与神经网络相结合的方法，由于小波分解序列在各自的区域尺度上有其各自的特点，因此应根据不同尺度上负荷变化的趋势来决定负荷预测的方法。为了提高预测精度的准确性，对不同尺度域应用不同神经网络分别进行建模和预报，其模型结构如图3所示。

模型的预测分为四个步骤：

1）运用小波对历史负荷数据序列进行分解，将历史负荷数据分解成细节分量以及趋势分量，即cd1、cd2、cd3以及ca3。

2）使用PSO来对网络的权值和阈值进行优化，使BP神经网络在初始阶段就拥有较优的初值。

3）对分解后的小波序列分别建模和预测。

4）对各个序列的预测值进行小波重构，生成负荷序列的最终预报。

图2 改进粒子群优化神经网络参数流程图

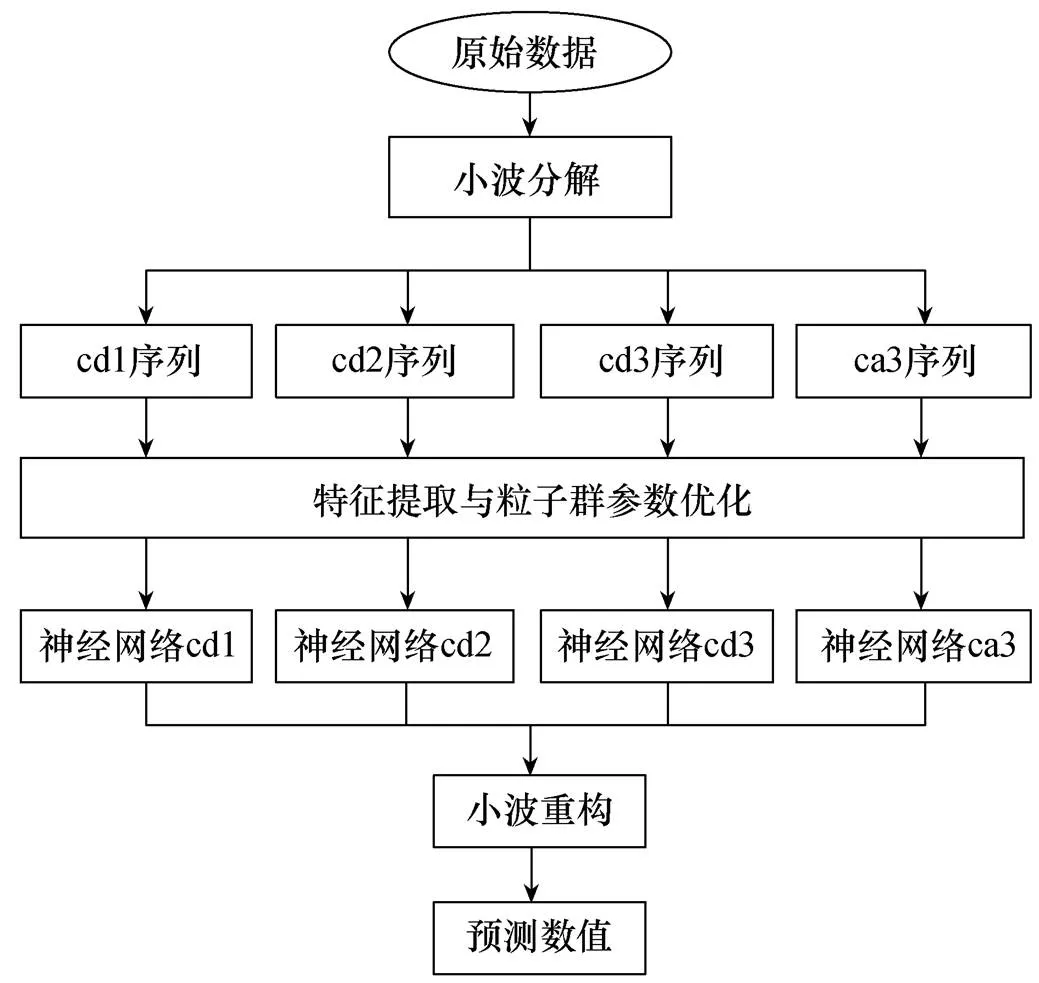
图3 建模流程图

5 算例验证

本文采用河南省某地区2019年5月份的负荷数据对未来一周的负荷变化进行预测。为了使预测数据和图像清晰，采用每天24个信息采集点。

5.1 小波分解

用小波变换（db3）和Mallat算法对负荷原有的数据序列进行3层分解。cd1、cd2、cd3分别为序列在各尺度下的高频部分；ca3为该序列的低频部分。

5.2 阈值处理

对分解后的高频部分应选择阈值，低频部分不再设阈值。根据以往对小波阈值选取的情况，本文采用改进粒子群优化算法寻找最佳阈值，与其他阈值估计方法进行对比，不同方法得到的阈值见表1。通过作用阈值，有利于后续神经网络的输入与训练。

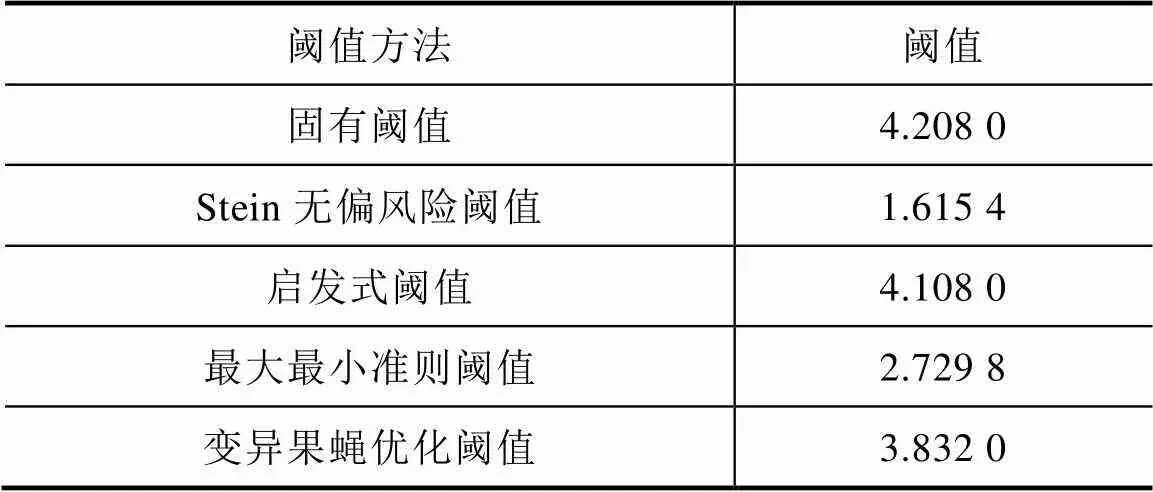
表1 不同方法阈值

5.3 各尺度域的建模和预报

本文的方法采用一个月的数据作为历史负荷序列。根据小波分解后的情况，对月负荷数据ca3、cd1、cd2、cd3建立各自的网络模型，每个模型都是3层，即输入层、隐含层和输出层。在预测过程中小波系数的变化随着负荷点数的变化而变化。在对样本集训练的过程中以误差在阈值以下来确定网络的连接权值，并且根据误差的大小调整连接权值。具体参数见表2。

表2 预测模型参数

5.4 综合预测结果

对以上负荷序列分别预测后，将结果相加重构得到最终的预测值。表3是本文所提出的小波分解粒子群优化BP神经网络方法与小波神经对一天24h负荷预测结果的比较。

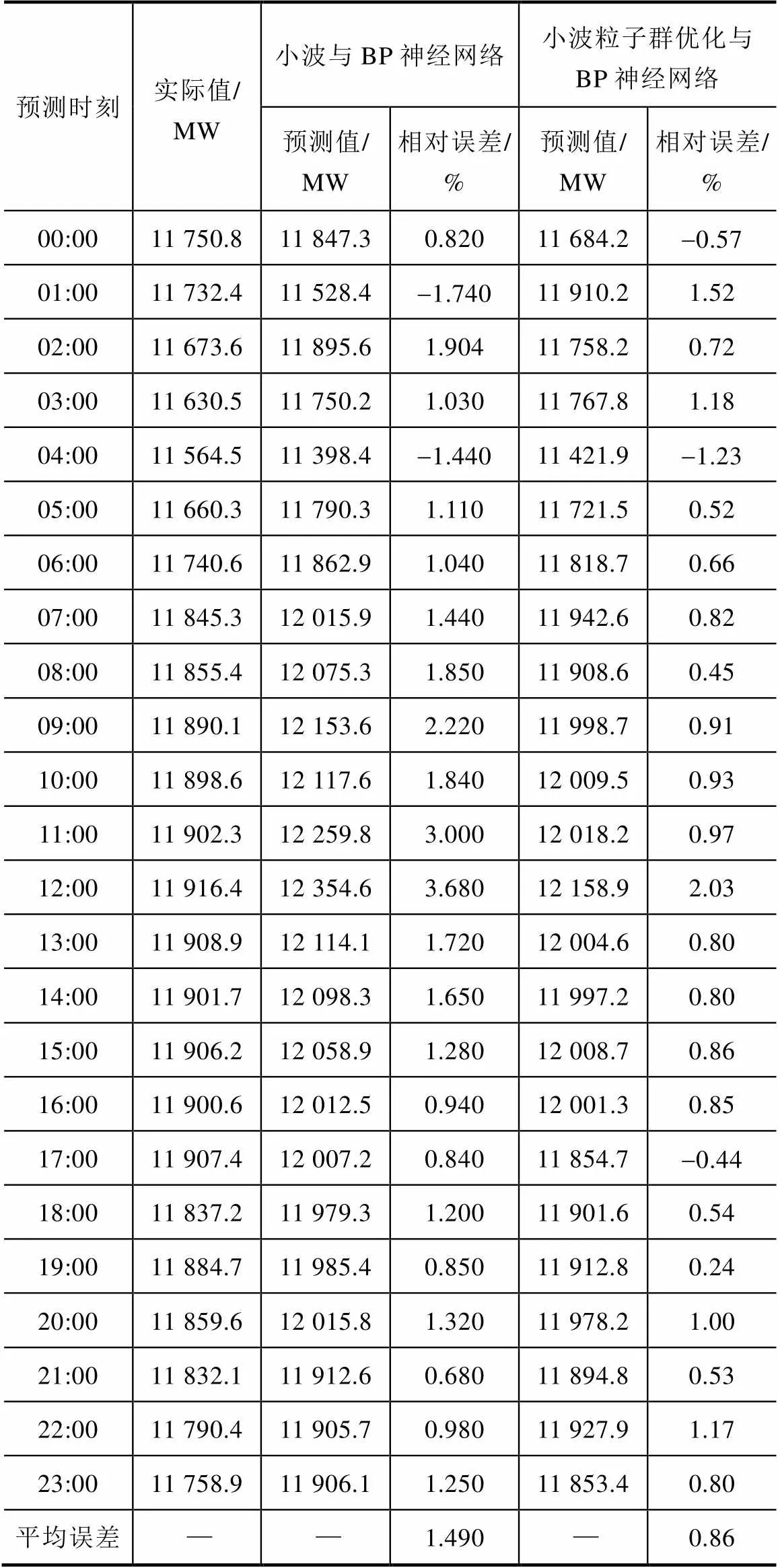
表3 24h负荷预测的结果

表4是本文方法所作的一周预测的平均相对误差统计结果，表5是将本文所提出的方法应用到另一地区进行负荷预测的结果。

将本文提出的方法与基本BP神经网络模型（BPNN）、改进粒子群优化BP神经网络模型（IPSO- BPNN）用相同的数据进行电力负荷预测，通过预测结果比较三种模型之间的优劣。

本文方法模型预测值与实际值对比图如图4 所示，本文提出的方法与基本BP神经网络模型（BPNN）、改进粒子群优化BP神经网络模型（IPSO- BPNN）的预测误差值对比图如图5所示。

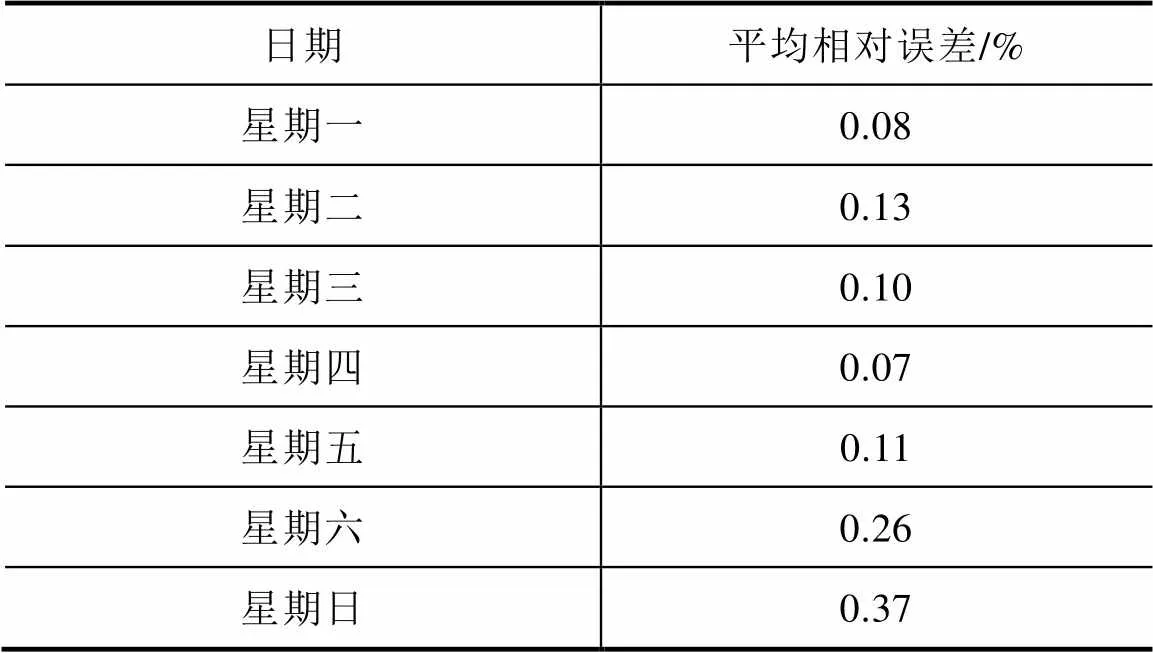
表4 一周的平均相对误差统计

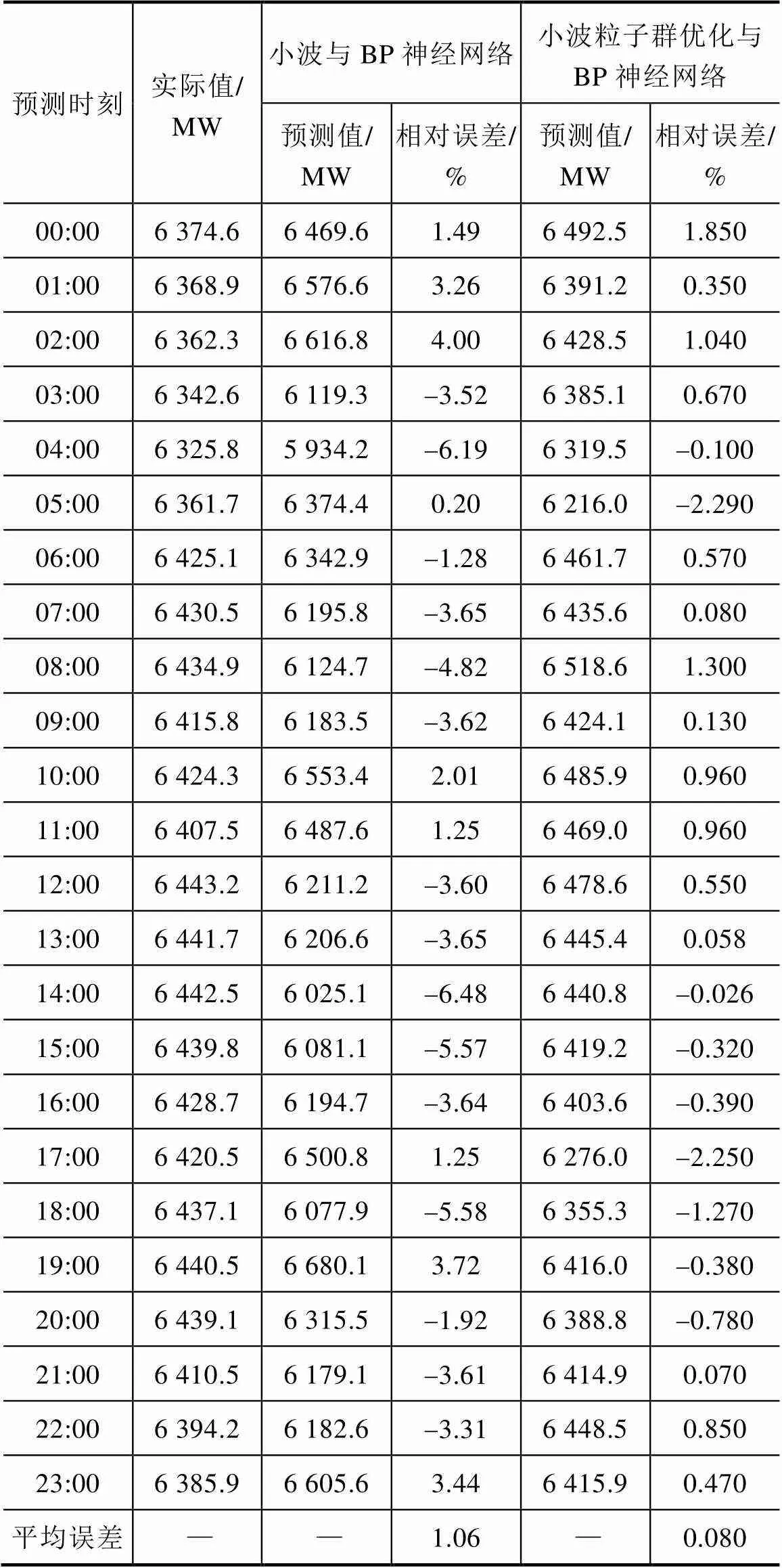
表5 24h负荷预测的结果

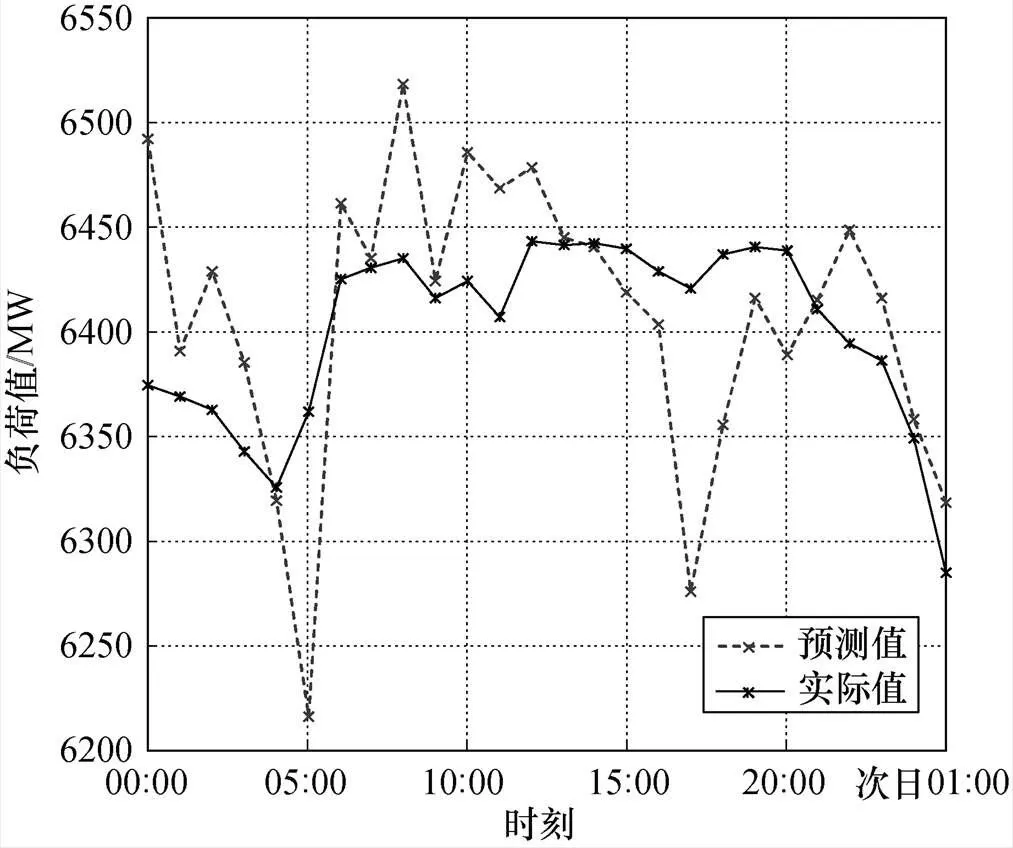
图4 本文所提方法预测值与实际值对比图

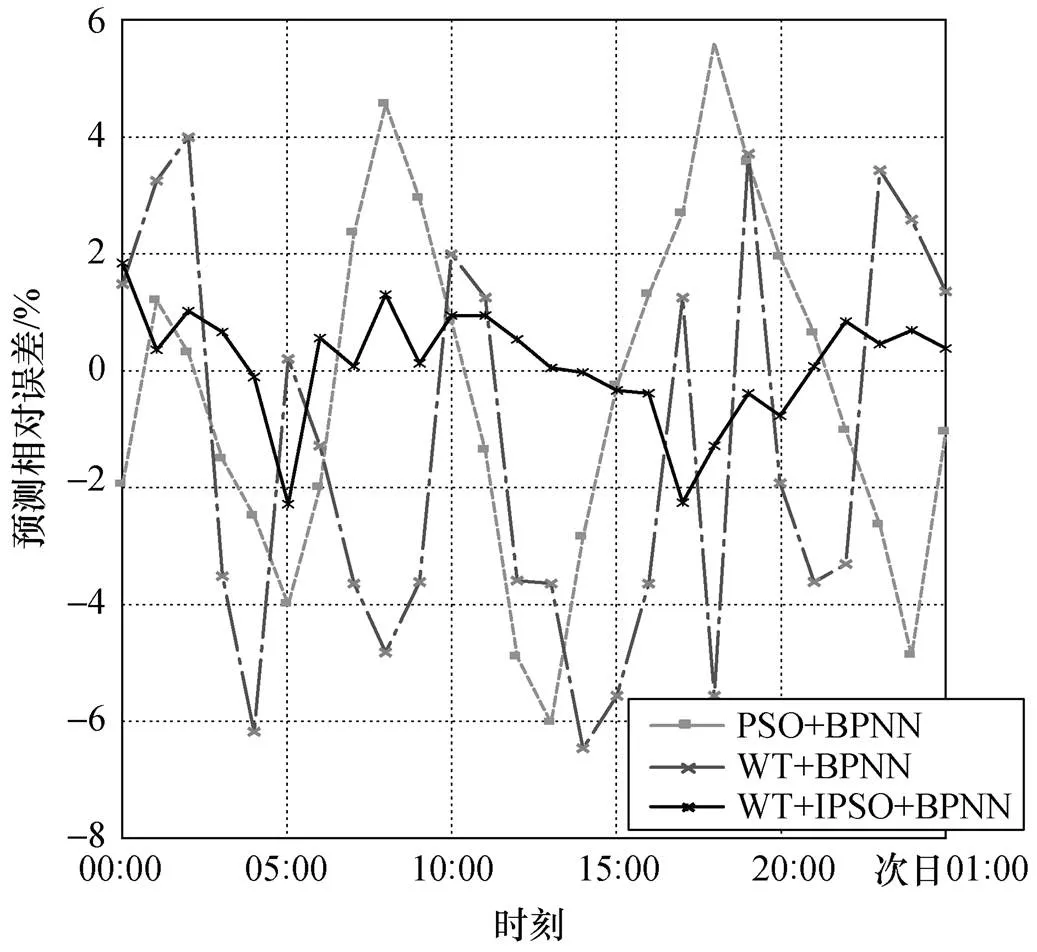
图5 预测误差对比图

采用方均根误差、平均绝对误差和平均绝对百分比误差三种预测性能指标进行比较，见表6，可以看出WT+IPSO+BPNN模型相比其他两种预测模型有更好的预测性能，其预测精度高于其他模型。

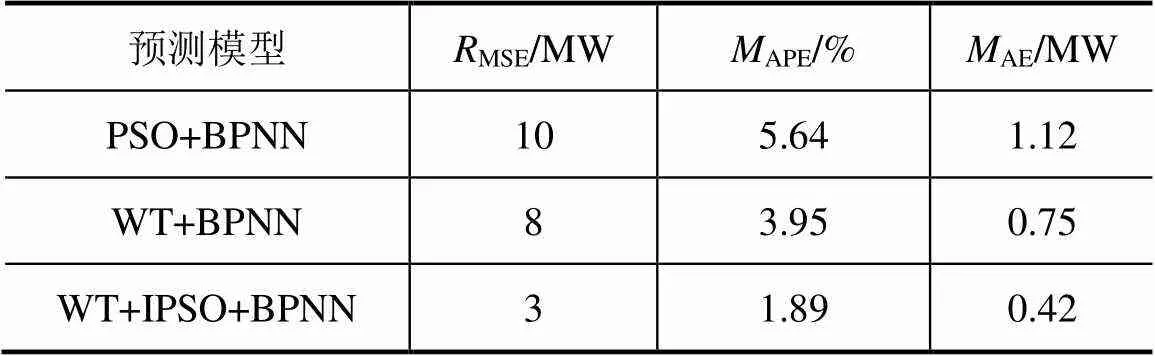
表6 模型预测结果比较表

6 结论

本文提出了基于小波分解粒子群优化BP神经网络相结合的负荷预测方法。通过小波分解把原始负荷序列分解为不同频段的序列，对这些不同频段的序列分别采用BP神经网络建模；由于BP神经网络在非线性数据处理方面的优势，将其作为短期负荷预测的基础模型。本文采用粒子群算法优化参数，改进粒子寻优过程，提髙了算法的全局收敛性；最后进行小波重构，得到负荷序列的最终预测结果。通过对两个地区分别以WT-BPNN和WT-IPSO-BPNN两种预测模型进行24h的仿真实验，结果表明，WT-IPSO-BPNN预测模型预测精度最高。并且以MSE、AE和APE为判断指标对比了PSO+BPNN、WT+BPNN和WT+IPSO+BPNN 3种方法的预测精度，本文所提的方法预测精度更高。本文提出的方法形成了“分解-预测-重构”模型预测，具有良好的预测精度和较强的适应能力，对于短期负荷预测有积极意义。

[1] 康重庆, 夏清, 刘梅. 电力系统负荷预测[M]. 北京:中国电力出版社, 2017.

[2] 蒋敏, 顾东健, 孔军, 等. 基于在线序列极限支持向量回归的短期负荷预测模型[J]. 电网技术, 2018, 42(7): 2240-2247.

[3] 王瑞, 王强强, 逯静. 基于随机神经网络的短期负荷预测[J]. 制造业自动化, 2019, 41(7): 44-48.

[4] 马天男, 王超, 彭丽霖, 等. 计及需求响应和深度结构多任务学习的电力系统短期负荷预测[J]. 电测与仪表, 2019, 56(16): 50-60.

[5] 李龙, 魏靖, 黎灿兵, 等. 基于人工神经网络的负荷模型预测[J]. 电工技术学报, 2015, 30(8): 225-230.

[6] 王玉龙, 崔玉, 李鹏, 等. 基于小波分析改进的神经网络模型电力系统负荷预测[J]. 电网与清洁能源, 2015, 31(2): 16-20, 27.

[7] 王增平, 赵兵, 纪维佳, 等. 基于GRU-NN模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(5): 53-62.

[8] 魏宏阳, 苏舟, 姚李孝, 等. 基于人体舒适度日特征向量的PSO-NN短期负荷预测[J]. 电网与清洁能源, 2016, 32(8): 135-140.

[9] 李若晨, 朱帆, 朱永利, 等. 结合受限玻尔兹曼机的递归神经网络电力系统短期负荷预测[J]. 电力系统保护与控制, 2018, 46(17): 83-88.

[10] 苏学能, 刘天琪, 曹鸿谦, 等. 基于Hadoop架构的多重分布式BP神经网络的短期负荷预测方法[J]. 中国电机工程学报, 2017, 37(17): 4966-4973, 5216.

[11] 宋学伟, 刘天羽, 江秀臣, 等. 基于改进鱼群算法与最小二乘支持向量机的短期负荷预测[J]. 电气技术, 2019, 20(11): 20-26.

[12] 丁坚勇, 朱炳翔, 田世明, 等. 改进F-score特征选择的MPSO-BP神经网络短期负荷预测[J]. 电测与仪表, 2018, 55(15): 36-41.

[13] 吴云, 雷建文, 鲍丽山, 等. 基于改进灰色关联分析与蝙蝠优化神经网络的短期负荷预测[J]. 电力系统自动化, 2018, 42(20): 67-74.

[14] 陆继翔, 张琪培, 杨志宏, 等. 基于CNN-LSTM混合神经网络模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(8): 131-137.

[15] 张平, 潘学萍, 薛文超. 基于小波分解模糊灰色聚类和BP神经网络的短期负荷预测[J]. 电力自动化设备, 2012, 32(11): 121-125, 141.

[16] 姜雲腾, 李萍. 基于改进粒子群神经网络短期负荷预测[J]. 电气技术, 2018, 19(2): 87-91.

[17] 王瑞, 周晨曦, 逯静. 改进粒子群优化BP神经网络短期负荷预测研究[J]. 制造业自动化, 2019, 41(6): 39-42, 77.

Short-term load forecasting based on WT-IPSO-BPNN

KANG Yi1,2SHI Liujun1GUO Gang3

(1. School of Electric Power, North China University of Water Resources and Electric Power, Zhengzhou 450045; 2. Zhengzhou Skong Electric Technology Co., Ltd, Zhengzhou 450001; 3. State Grid Hebei Electric Power Co., Ltd, Handan Power Supply Company, Handan, Hebei 056000)

In order to improve the accuracy of short-term load forecasting, a combined forecasting model based on wavelet decomposition (WT), improved particle swarm optimization (IPSO) and BP neural network is proposed. Firstly, we use wavelet decomposition to preprocess the load data, and decompose the historical data into cd1, cd2, cd3 and ca3; then we use neural network to model and predict the decomposed wavelet sequence; finally, we use wavelet to reconstruct the final forecast of the load sequence. In view of the accuracy of BP neural network samples and to increase the convergence speed and stability of the neural network, the improved particle swarm optimization method is used to optimize the network, forming a “decomposition prediction reconstruction” model. Compared with the wavelet decomposition BP neural network method, it has stronger training and learning ability, faster convergence speed, high prediction accuracy and strong adaptability.

wavelet decomposition; particle swarm optimization (PSO); BP neural network (BPNN); load forecasting

河南省科技攻关项目（182102210335）

河南省高等学校重点科研项目（19A470002）

河北省电力公司科技项目（5204HD20000N）

2020-04-11

2020-07-25

康 义（1987—），男，硕士，主要研究方向为电力系统运行与控制技术。