关帝山华北落叶松林分直径分布规律研究
秦 舟,张梦弢
(山西农业大学 林学院,山西 太谷 030801)
直径结构作为最基本的林分结构,直接影响着林木相关因子的变化[1]。同时,为林分直径未来生长状态预测提供了理论依据。在林分中,直径大小的表达形式是径阶,其大小分布在林分结构、森林调查和研制林分材种出材量表中至关重要[2-3]。所以,直径分布模型研究对制定森林管理计划有着很重要的意义。
林分直径结构模型是国内外林学家关注和研究的焦点,很多学者都在研究直径分布模型,有许多不同的理论概率密度方程都被用来描述森林的直径分布,主要包括Weibull分布、负指数分布、正态分布、β分布、Johnson's SB函数分布、τ分布等,他们利用这些模型来预测未来林分发展状况[3-9]。龚直文等[10]运用负指数函数在长白山对杨桦次生林(Populusdavidiana-Betulaplatyphyllasecondary forests)分析直径分布模型。周新年等[11]运用负指数分布模型对天然林林分直径分布进行预测,构建了具有时间序列的直径分布预测模型,为林分生长动态的研究奠定了基础。周国模等[12]利用Weibull分布3参数与林分特征因子间的相关关系,导出了一个改进的二元分布模型,很好地测度了浙江省毛竹(Phyllostachysheterocycla)林胸径和年龄分布规律;夏晓波等[13]使用Weibull分布函数研究日本落叶松(Larixkaempferi)时,编制了直径分布预估概率表;杜志等[14]以长白山地区6块云冷杉(Piceajezoensis-Abiesnephrolepis)林样地调查数据为基础,采用限定混合Weibull模型方法,对直径分布进行了模拟,发现限定混合模型是一种较好的具有高灵活性和高精度的林分直径模拟方法;张梦弢等[15]运用3种不同的直径结构分布模型对云冷杉混交林进行拟合发现,在3种分布模型中,负指数分布拟合近似倒J形曲线时效果较好,限定混合Weibull模型在拟合不规则直径分布时效果较好;石振威等[16]采用Weibull分布模型拟合针栎混交林,发现Weibull分布函数和更适于拟合针栎全林分和栎类(Quercusacutissima)林分的直径分布规律。
华北落叶松(Larixgmeliniivar.principis-rupprechtii)作为华北地区的主要树种之一,具有重要的地位,近年来以华北落叶松为对象的研究层出不穷,如温永斌等[17]以山西太岳山华北落叶松、油松(Pinustabuliformis)林分为对象,运用相关模型对该地区森林生态系统的碳水循环相互作用进行深入研究;李慧婷[18]以青海华北落叶松为对象,对其直径分布和树干材积模型进行拟合,表明β分布及Richards模型分别在拟合直径分布和树干材积方面效果较好;仅有的直径分布研究如周泽宇等[19]以线性混合效应模型拟合华北落叶松直径分布结果表明,塞罕坝华北落叶松人工林直径分布最优模型为Weibull分布。但是上述研究对于不同状态下林分直径结构不同分布状态拟合相对较少。本研究以庞泉沟自然保护区华北落叶松林分为对象,通过对林分直径结构进行拟合,了解此时林分直径分布状态,为今后林分直径分布的调查提供捷径,较全面地了解林分生长动态,为林分抚育间伐技术的确定和实施,以及林分结构的调整提供一定的技术支持和理论依据。
1 材料与方法
1.1 研究区概况
研究地选择在关帝山庞泉沟自然保护区,位于山西省交城县西北部和方山县东北部交界处,地处吕梁山脉的中部,111°22′-111°33′E,37°45′-37°55′N,海拔1 800~2 830 m,保护区南北长15 km,东西宽14.5 km,总面积10 443.5 hm2,森林覆盖率达85%[20]。保护区地处暖温带大陆性季风气候区,年平均气温4.3℃,极端最高气温32℃,极端最低气温-26.1℃,7月平均温度18℃,1月平均温度-12.4℃。大部分地区≥10℃的积温1 800℃~2 950℃。无霜期100~125 d。年平均降水量822.6 mm。庞泉沟自然保护区是山西森林面积及森林蓄积量最大的自然保护区,层次复杂、结构完整、树种丰富。植被具有明显的垂直带谱,海拔1 800 m以下主要以温性灌丛、落叶阔叶林、温性针叶林和温性针阔叶混交林为主;1 800 m以上区域主要以寒温性针叶林和亚高山灌丛草甸为主[21]。主要树种有油松、蒙古栎(Quercusmongolica)、山杨、白桦、华北落叶松、侧柏(Platycladusorientalis)、云杉(Piceaasperata)等。
1.2 样地概况
2017年在庞泉沟自然保护区内的八道沟和卧牛坪地区,在实地踏查的前提下,选择林相较好、具有代表性的地块布设9块0.09 hm2(30 m×30 m)的样地,对样地中立木进行每木检尺,实测胸径、树高、冠幅、坐标等基本调查因子,并对每株立木进行树种鉴定(表1)。由于选取样地面积较小,样地上林木株数少,研究采用每4 cm径阶为1个径阶进行划分,并将所得数据统计进表。由表1可知,选取的9块样地之间林木株数差距很大,林木最多的5号样地达到了90株,而最少的3号样地仅有37株。平均胸径最小的是7号样地,为21.6 cm,最大的是4号样地,为30.1 cm,各样地之间差距较大。大部分样地直径分布范围不大,变动系数>0.45的样地仅有3号、8号和9号样地。

表1 关帝山华北落叶松林分概况Table 1 General situations of L.gmelinii var.principis-rupprechtii forest in Guandi Mountain
1.2 研究方法
1.2.1 Weibull分布 Weibull分布具有求解方法多样、求解简单的优点,无论是在同龄林还是异龄林或者其他类型的林分结构研究中均取得了很好的拟合效果[22-23]。
Weibull分布计算公式:
(1)
式中,a为位置参数,也就是直径分布最小径阶下限值;b为尺度参数、c是形状参数、e为自然对数的底,x为对应的径阶直径,f(x)为对应各径阶的株数百分比[24]。
1.2.2 负指数分布 未受干扰的天然异龄林趋于一个可用指数方程表达的直径分布[10]。负指数分布计算公式为:
f(x)=ae-bxx≥0,b>1
(2)
式中:x为胸径;a、b表示直径分布特征的常数,其中,b表示林木株数在连续的径阶中减小的速率,a为林分相对密度[10]。
1.2.3 限定混合Weibull分布 限定混合模型的公式为[13]:
(3)
式中,可看作k个三参数Weibull模型组成的,由于本研究仅考虑2~3组分的限定混合情况,其拟合情况分别表现为双峰和三峰,因此原式分别可表达为
双峰Weibull模型:
f(x)=ρ1f1(x)+ρ2f2(x),ρ1+ρ2=1
(4)
三峰Weibull模型:
f(x)=ρ1f1(x)+ρ2f2(x)+ρ3f3(x),ρ1+ρ2+ρ3=1
(5)
式中,ρi表示第i个组分所占比例,0≤ρi≤1且;∑ρi=1;fi(x)表示第i个概率密度函数,每个概率函数都有不同的平均值、方差。用ai、bi、ci(i≤3)来分别表示位置、尺度和形状参数,并通过R语言的mixdist包完成参数的计算[15]。
1.2.4 检验方法 使用偏差(Rias)和均方根误差(Rmse)检验3种模型的拟合效果,并进行卡方检验测量模型的拟合度。
(6)
(7)
(8)
式中,Ni为该径阶实测值; 为该径阶模型拟合值;m为径阶数;χ2的自由度为(m-k-1),其中k为参数值。
2 结果与分析
2.1 直径分布拟合
表2样地3中3参数模型形状参数c=5.780,模型拟合曲线呈现右偏分布除此之外均为正偏山状。在限定混合Weibull模型中,只有6号样地为3部分组成,其余均由2个组分组成,而且由于6号样地第3个组分的形状参数c3值为12.993,使得分布曲线向左偏移。其余2组分的混合分布模型中,第1组分直径分布为正偏山状,在第2组分中形状参数c2值只有5号和8号样地是正偏山状分布,其余均为左偏态分布。
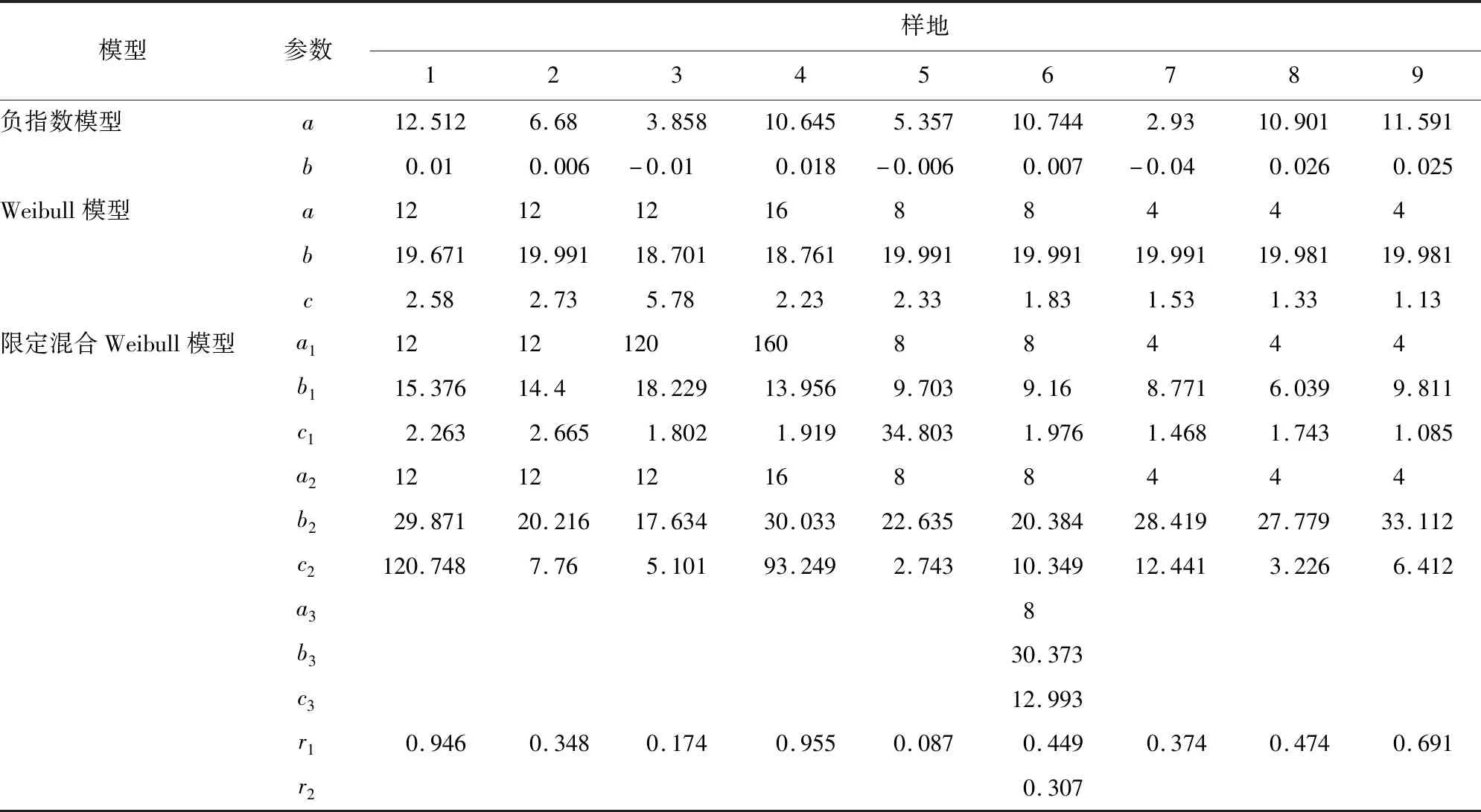
表2 关帝山华北落叶松林3种直径分布模型的参数Table 2 Parameters of three diameter distribution models of L.gmelinii var.principis-rupprechtii forest in Guandi Mountain
图1为各样地直径分布直方图和3种分布函数的拟合曲线,1号、2号和4号样地符合正态分布,3参数Weibull模型拟合效果较好;3号样地呈现明显的单峰曲线,峰值在30 cm处,3参数和限定混合模型拟合精度较好;5号样地也呈现出近似双峰分布的曲线,峰值为18 cm和26 cm;7号样地为近似双峰分布曲线,峰值分别为14 cm和34 cm;对于5号样地和7号样地,限定混合模型拟合效果优于其他模型;6号样地呈现类似3峰分布曲线的,也同样是限定混合Weibull分布模型拟合效果好;8号样地和9号样地在图中显示近似反J型曲线,负指数模型呈现的效果更好。

图1 关帝山华北落叶松林9块样地3种直径分布模型的拟合效果Fig.1 Fitting effect of three diameter distribution models for 9 sample plots of L.gmelinii var.principis-rupprechtii in Guandi Mountain
2.1 拟合检验
表3利用均方根误差(rmse)、平均偏差(bias)和χ2值以及P值对所得样地数据进行检验。同一样地上,不同直径分布模型的平均偏差和χ2越小且P值越大的话,则该直径分布模型拟合效果越准确。例如2号样地上3参数模型拟合效果最好,因为该模型的P值最大且平均偏差和χ2最小,同理1号和4号样地也均是3参数模型为最优拟合效果。而8、9号样地呈现较明显的反J型曲线,平均偏差与χ2值也反映负指数分布模型的拟合精度更高。3号样地上负指数模型与限定混合模型P值相差不大,但后者的平均偏差和χ2值比前者小,故3号样地上限定混合模型精度较高。其余样地上限定混合Weibull模型的P值远大于其他模型,所以拟合精度高于其他模型。
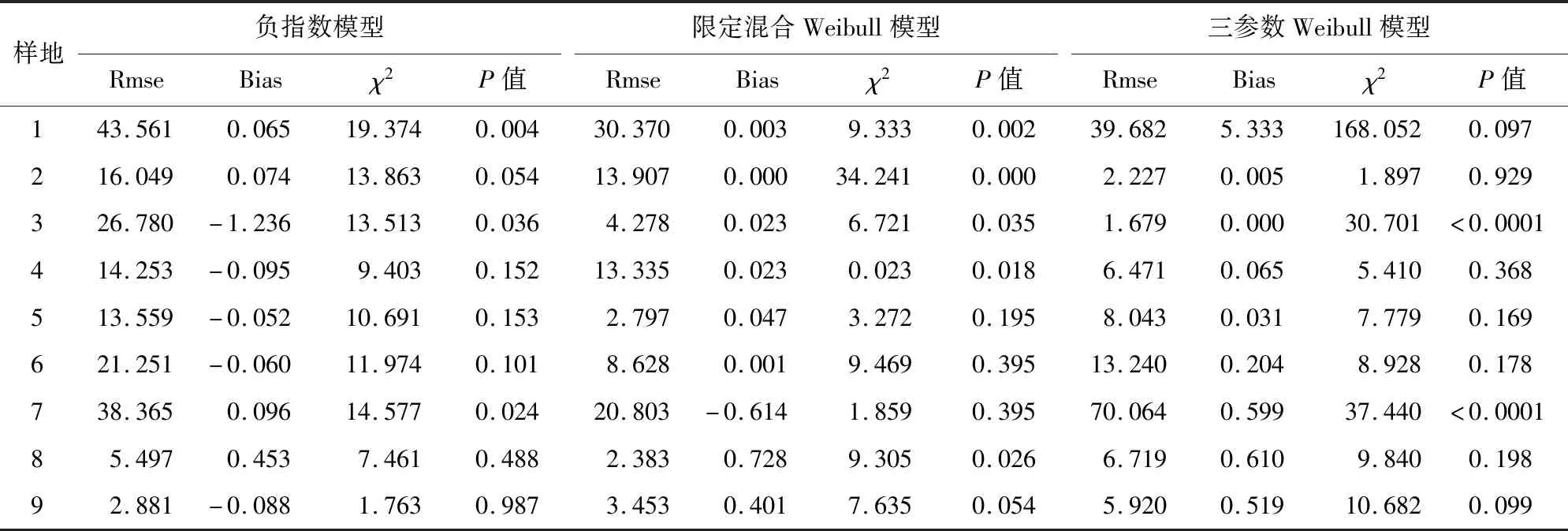
表3 关帝山华北落叶松林3种直径分布模型的检验结果Table 3 Test results of three diameter distribution models of L.gmelinii var.principis-rupprechtii in Guandi Mountain
图2较为直观地反映出1号样地中各模型的残差在初始和中间径级波动剧烈,呈现出交替波动的现象,并且随着径级的增大,3种模型残差的波动幅度逐渐降低。2号和3号样地的3参数Weibull模型在样地上所有径级内的残差波动都较小。4号样地3种模型在前几个径级内残差波动不大,在后几个径级内残差先增后减。6号样地内限定混合模型残差除第1个径级外,整体波动不大,而7号样地上3种模型则随着径级的增大,残差波动幅度也越来越大。5号样地3种直径分布模型残差波动比较稳定,整体上变化幅度不大。9号样地全径级上3种直径分布模型残差值均较低,而8号样地除前几个径级外,3种模型残差值也跟9号样地情况类似。

图2 关帝山华北落叶松林9块样地3种直径分布模型拟合结果的残差值Fig.2 Residuals of fitting results of three diameter distribution models for 9 sample plots of L.gmelinii var.principis-rupprechtii in Guandi Mountain
3 结论与讨论
在森林经营中,直径分布拟合模型要求高精度和高灵活性,合理运用不同的模型以及非参数方法不可或缺。本研究采用3种模型进行模拟比较,在不同样地内各模型的拟合效果各不相同。研究分析发现3种不同直径分布模型分别有其各自的最适用环境。若林地上林木株数随径级的增大而逐渐减少,呈现反J型分布时,负指数直径分布模型能够更好的拟合林木在各径级上的分布情况,该模型可为幼龄林的抚育采伐提供合理的依据。Weibull直径分布模型对于明显单峰山状分布的人工林分,预测结果更准确可靠。而对于呈现不规则多峰山状的林分,限定混合模型的拟合效果更好。在反J型分布曲线的样地上负指数模型拟合效果更好,单峰分布的情况更适用Weibull模型和限定混合模型,而限定混合Weibull模型在拟合双峰及多峰型直径分布林分时的精度更高。1~6号样地为华北落叶松纯林,其中1号、2号和4号样地呈现出正态分布,试验表明该林分直径结构相对单一,为同龄纯林;3号、5号和6号样地呈不对称单峰或多峰曲线,为次生异龄林;7~9号样地为混交林,7号样地为近似双峰曲线,8号和9号样地呈现反J型曲线,直径结构相对复杂,这与异龄混交林的规律相一致,这种状态下该林分能够维持天然更新,且大径阶林木保持一定数量,表明该生态系统稳定性较好[25]。
由于选择样地面积较小,因此在划分林分径级时采用生产上常用的4 cm划分法。在测量过程中,由于小径阶的林木过少,造成模型拟合中各样地起测径阶不同,造成了模型的拟合精度与评价有一些影响。小径阶林木过少可能是因为人为的频繁干扰所致。因此,我们在减少对林木破坏的同时,要保护林下天然更新,或者进行人工林下补植等,保证天然林的健康更新机制[15]。
本试验通过对3种直径分布模型的拟合发现,纯林林分样地的峰值多出现在30 cm左右径阶处,混交林的峰值则多出现在小径阶,应采用不同措施对该林分进行适度调整。若林分为幼龄林或中龄林,采用封育措施;若林分为成熟林,则选择进行适度择伐;若大径阶林木过多时,对该径阶的林木进行适度采伐。
利用直径分布模型分析林分结构,可为林分经营提供依据和措施,从而提高林分结构的多样性[26]。本次研究收集关帝山华北落叶松纯林和混交林地的数据,运用3种模型对该地林分进行拟合,结果表明该地林分相对合理,但也需要进行一定的调整,从而改善该地林分的经济和生态效益。下一步研究重点是通过及时复测及收集信息,得到样地林分直径的平均状态,以期更好地提高该地区华北落叶松的直径结构拟合精度。根据不同调查期内数据变化,分析该地区林分结构动态变化。同时,利用该样地林分的直径结构模型,规划和调整该地区现有林的结构,加快森林群落结构的恢复速度,促进该地区林分健康发展。

