基于时空独立的随机森林模型对海南热带气温数值预报的订正
陈有龙,宁雨珂,唐荣年,谢小峰
(1. 海南省南海气象防灾减灾重点实验室,海南 海口 570203;2. 海南省气象台, 海南 海口 570203;3. 海南大学 机电工程学院, 海南 海口 570228)
数值预报已发展多年,随着技术水平的提高,数值模式方法越来越完善,其预报精度亦越来越高,它是当前主要的客观预报工具之一[1].但是,数值预报模式仍无法完全达到真实模拟大气的程度,因此研究有效的和科学的订正方法至关重要.通过对数值预报结果进行订正,可提升气象预报的精度,这对防灾减灾和经济发展具有重要的意义[2].尤其是在海南,由于其独特的热带气候以及海岛地理地貌,数值预报的结果远不能满足要求,因此迫切需求高水平的预报订正方法.
传统的订正方法主要是通过统计学的方法来修正大气动力方程的误差,而根据订正思路的不同又可采用不同的模型来实现.比如,薛堪彬等[3]从空间误差订正的角度提出了一种滑动双权重平均订正法,他们对欧洲中期天气预报中心(ECWMF)髙分辨率模式的2米最高和最低温度进行了偏差订正和误差分析;李佰平等[4]从消除时效偏差的角度提出了一种结合一元线性回归、多元线性回归、单时效消除偏差和多时效消除偏差平均的综合订正技术,对ECMWF模式的地面气温预报进行了订正;张玉涛等[5]则从自适应偏差订正的角度提出了一种基于一阶自适应卡尔曼滤波的订正方法,对GRAPES 3千米模式的2米气温、2米相对湿度和10米风开展了偏差订正.传统的订正方法均是基于假设条件而展开统计学建模,并通过模型来实现预报偏差的订正,然而这类方法并没有充分利用数据所包含的丰富订正信息,容易受到各种假设条件的限制,存在一定的局限性.
随着机器学习的发展,越来越多的研究者开始使用基于数据驱动的机器学习方法来进行预报偏差的订正[6],他们通过对大量的历史实测数据和历史预报数据进行深度挖掘,弄清了实测和预报偏差的关系,再反过来利用这些关系对最新的预报结果进行订正,这样就提高了预报的准确性.此类方法完全依托于数据本身,具有很强的鲁棒性.基于数据驱动的机器学习方法非常多,应用于数值模式预报结果的订正也很多,比如王焕毅等[6]和倪铮等[7]分别采用BP神经网络和LSTM深度神经网络,对数值模式数据和实况观测数据进行学习,建立了数值模式气温预报误差客观化订正的模型,其区别就在于所选用的模式不一样,且所选择的实况气象要素不一样.随机森林具有高度线性化的特点,故其也被广泛应用于天气预报的订正,例如:Ho等[8]引入空间回归法来绘制相对于参考站的典型炎热夏季白天的峰值气温,并用随机森林对实地观测数据进行了校准;Cho等[9]使用随机森林来处理本地数据和多个模式预测数据;李文娟等[10]将随机森林算法应用于强对流的潜势预测和分类,分短时强降水、雷暴大风、冰雹和无强对流4种类别;刘扬等[11]运用随机森林算法,构建了暴雨灾害中人口损失的预估模型,并以精细化网格降水的实况分析和预报产品驱动模型,预估是否发生人口损失.此类方法对多个站点和多个预报时刻均是采用统一的随机森林模型,但是当多个站点覆盖的区域存在多种气象类型时,会积累模型的误差,从而影响预报精度.海南岛就是属于此种情况,由于其独特的热带气候以及海岛地理地貌,海南岛南北的气候差异较大,且变化快,因此全岛区域无法直接采用统一的随机森林模型.
基于此,针对海南岛的气候特点,本文提出了一种基于时空独立的随机森林模型,同时,通过挑选合理的气象要素及预报模式,对全岛18个市县的站点,采用分站点分时段的建模方式,实现了对海南岛18个市县气温数值预报的订正,得到了高精度的预报结果.
1 实测及模式数据的分析
基于数据驱动的订正方法需要从历史实测数据和模式预报数据拟合出实测和预报偏差的关系,而实测数据和模式数据包含较多的要素,并且存在缺失等情况,这些都会影响到模型训练的效果.因此,对实测数据和模式数据的预处理至关重要.为此,本文针对海南岛气温数值进行模式订正,分别对实测数据和模式数据进行要素选择,如表1所示.

表1 实测数据和ECWMF模式数据的要素列表
在实测数据方面,本文的实测数据主要包括了海南省18个市县站点(海口、东方、临高、澄迈、儋州、昌江、白沙、琼中、定安、屯昌、琼海、文昌、乐东、五指山、保亭、三亚、万宁、陵水)的实际观测数据.考虑到对气温订正的需求,从每个站点挑选了8个相关的实测要素,它们分别是风向(Wd2m)、风速(Ws2m)、气温(TT)、最高气温(Tmax)、最低气温(Tmin)、相对湿度(RH)、本站气压(pp)和1小时降水量(R1h)作为模型输入数据.实测数据是从站点传感器采集而来的,会出现缺省情况.针对此情况,本文采用前后插值的方法来弥补缺省值.
在模式数据方面,本文主要运用ECMWF模式的网格预测数据.由于网格点的经纬度和真实站点的经纬度存在偏差,故本文采用右上角原则,根据真实站点的经纬度,找到右上角与其最近的网格点,并将其作为站点对应的网格点,然后针对每个选定的网格点,分别抽取出近地要素和高空要素,并将它们作为模型的输入数据.近地要素主要包括地表10米U风分量(U10m)、地表10米V风分量(V10m)、地表2米露点温度(D2m)、地表2米温度(T2m)、地表对流有效势能(CAPE)、海面平均海平面压力(MSL)、地表低云量(LCC)等七个气象要素.高空要素则是分别从200 kPa、400 kPa、500 kPa、700 kPa、850 kPa、925 kPa、950 kPa等七个高空层来提取以下6个气象要素,即位势高度(GH)、相对湿度(RH)、温度(T)、东西风(U)、南北风(V)、垂直速度(S).
2 基于时空独立的随机森林模型


(a)(b)图1 样本构造及分段训练

其中,R1,R2和c1,c2分别表示每个节点划分出来的两个样本子集和每个样本子集中每个样本的特征均值,通过遍历每个样本的每个特征,以寻求使得上式最小的划分特征与划分特征值,然后依次构造NT棵回归决策树,每棵树均能回归出数据和气温标签的关系,再将所有树回归出来的气温值进行平均,如此就得到最终的回归结果,并形成了随机森林模型.最后,如图1(b)所示,逐站点逐3小时构建相应的随机森林模型,并对每个站点进行时空的解耦,这样就实现了对全岛模式预报气温的精准订正(表2).

表2 基于时空独立的随机森林算法
3 结果与讨论
3.1 性能评价指标为了验证所提订正方法的有效性,本文采用了三个温度预报的常用性能评价指标,即小于2 ℃的准确率、小于1 ℃的准确率以及均方根误差,对真实温度、ECMWF模式预报温度和本文模型预报温度的预报效果进行了评估.
小于2 ℃的准确率和小于1 ℃的准确率可以定义为:
其中,N表示预报的总次数,Nr表示预报正确的次数.当Nr是预报值和真实值误差在1 ℃以内的次数时,则k=1,此时TT1是小于1 ℃的准确率;当Nr是预报值和真实值误差在2 ℃以内的次数时,则k=2,此时TT2是小于2 ℃的准确率.
均方根误差指标定义为:
其中,xi是预报值,x是真实值,N是预报次数.
3.2 单点订正精度分析以2020年4月16日海口站点为例,预报时效为7天,时效间隔为3小时,分别采用小于2 ℃的准确率、小于1 ℃的准确率及均方根误差等3个指标,对真实温度、ECMWF模式预报温度和本文模型订正结果进行比较,结果如图2所示.本文所提模型能够对ECMWF模式气温预报结果进行较好地订正,在三个指标上均优于ECMWF的预报结果,能更加准确地逼近真实温度,这证明了本文算法在单点订正的有效性.
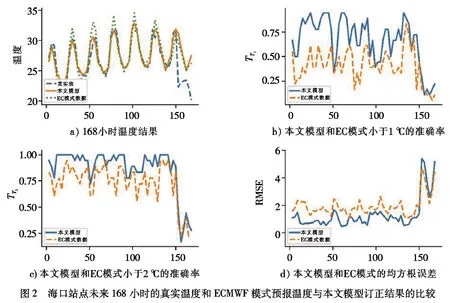
图2 海口站点未来168小时的真实温度和ECMWF模式预报温度与本文模型订正结果的比较
在对基于时空独立随机森林模型进行模型学习时,随机森林中树的数量(NT)和特征数占比(NF)会对回归结果产生较大的影响,因此,本文采用网格化搜索的方式对这两个参数进行了分析,确定了最优参数组合.将训练集按7∶3的比例分成两部分,一部分用来训练模型,一部分则用来验证模型,以选出最优参数.本文设定树的数量搜索范围为400~1 300,特征数占比的搜索范围为10%~90%.网格化搜索的结果如图3所示,从图3中可知,当特征数占比在范围[50%~75%]时,且树的数量在[400~1 300]时,本文模型的性能稳定在某个固定的区间,波动不大,这也证明了本文所提算法具有较好的鲁棒性.因此,在综合考虑运算时间和效率的基础上,本文最终选取了树的数量为1 000,特征数占比为75%.此外,为说明本文所提的随机森林算法在气象预报方面的优越性,在此将随机森林模型与基于Boosting的GBDT模型和传统线性回归模型进行对比.仍以海口站点为例,分别采用了三个模型进行预测,结果如图4所示.从图4中可以看出,本文所提模型的准确率高于GBDT和传统线性回归的准确率.
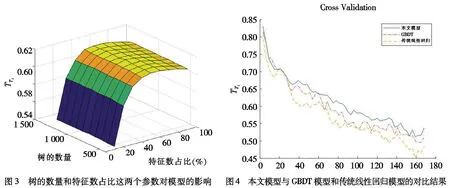
图3 树的数量和特征数占比这两个参数对模型的影响图4 本文模型与GBDT模型和传统线性回归模型的对比结果
3.3 区域订正精度分析在单点订正性能优越的基础上,本文接下来分析了海南岛18个站点的区域订正结果,即采用本文建立的时空独立随机森林模型对海南岛的18个站点同时进行订正,并以2020年4月16日T08开始起报,预报时效为7 d,时效间隔为3 h,分别显示未来3 h、12 h、24 h、48 h和120 h的预报气温值和真实值.如图5所示,与第一行的真实气温值比较,基于时空独立的随机森林模型能够很好地对ECWMF模式预报值进行很好的区域订正,在海南岛区域,它比ECWMF模式的预报结果更加精准.
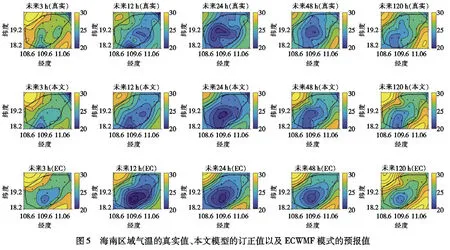
图5 海南区域气温的真实值、本文模型的订正值以及ECWMF模式的预报值
为了进一步分析区域订正的结果,图6展示了18个站点小于1 ℃的准确率结果,同样,以2020年4月16日T08开始起报,图6纵坐标为未来7天的总准确率,横坐标则是18个站点,从图6可以看出,本文所提的时空独立随机森林模型能够对18个站点的ECWMF模式预报结果进行同时订正,并且能让18个站点的结果更加准确,这也验证了本文所提算法在区域订正的有效性.
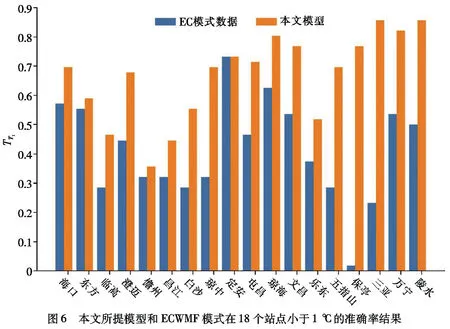
图6 本文所提模型和ECWMF模式在18个站点小于1 ℃的准确率结果
3.4 时空独立特性分析为了进一步验证本文所提方法在海南岛区域订正的优越性,下面对比了分站点订正的随机森林模型和所有站点采用统一订正的随机森林模型,并对本文所提的时空独立特性进行了分析.图7展示了两种模型在海南岛的订正效果,图7中黑色实线是订正结果,背景颜色区域则是真实温度场.图8则展示了两种模型在18个站点的预报准确率情况.从图7和图8中可知,总体而言,这两个模型均能实现对ECWMF预报值的精准订正,但是在个别局部区域,比如海口—临高、乐东—五指山、琼海—万宁,本文所提的时空独立随机森林模型的订正效果要优于采用统一模型的订正效果.
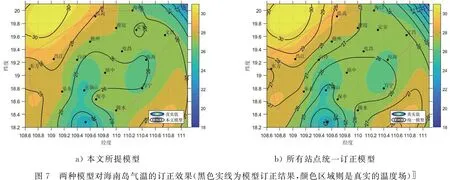
a) 本文所提模型b) 所有站点统一订正模型图7 两种模型对海南岛气温的订正效果(黑色实线为模型订正结果,颜色区域则是真实的温度场)〛
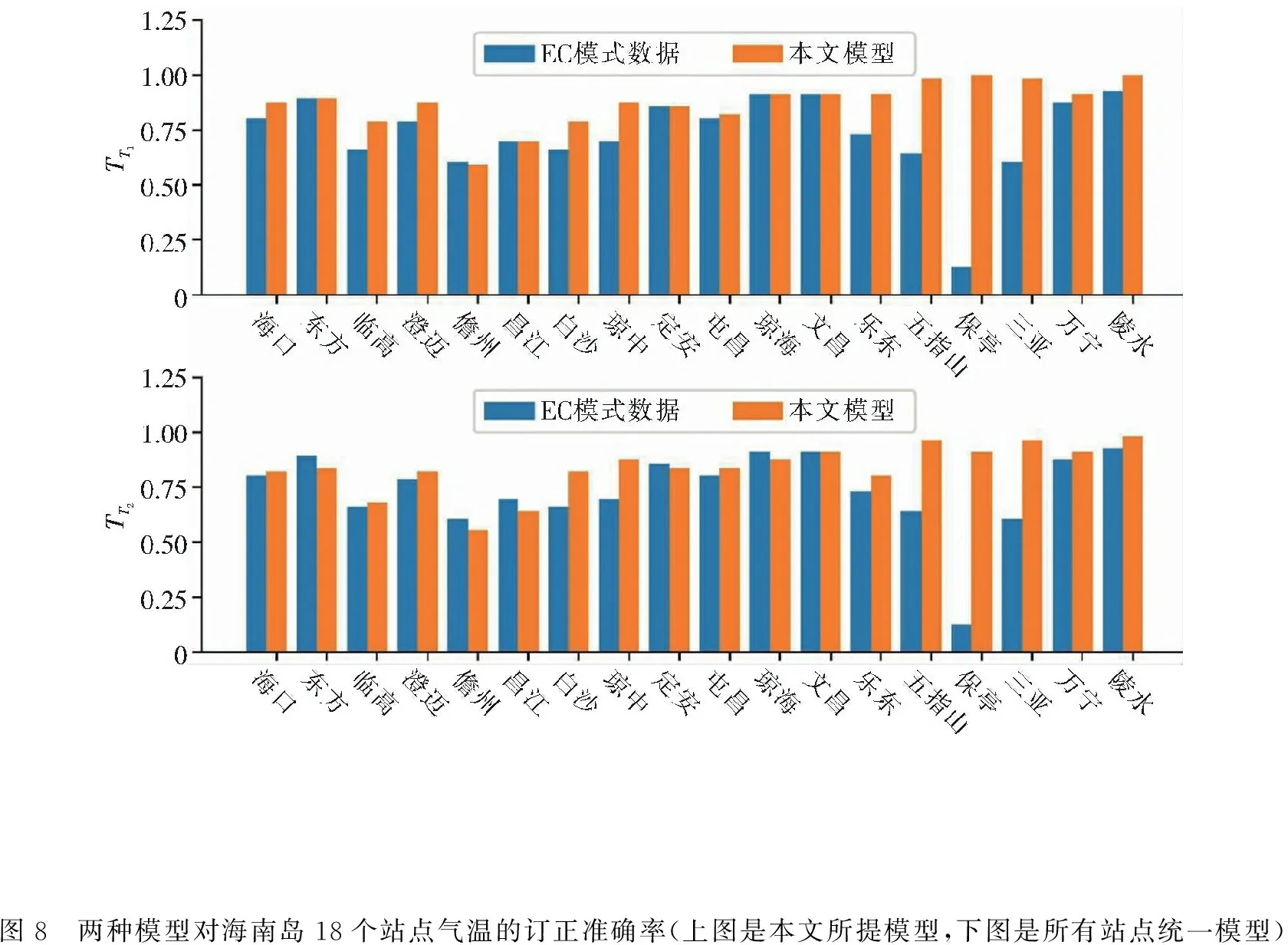
图8 两种模型对海南岛18个站点气温的订正准确率(上图是本文所提模型,下图是所有站点统一模型)
最后针对海口—临高、乐东—五指山、琼海—万宁三个局部区域,分别分析了表1中的各个气象要素对两种随机森林模型的影响情况.对于海口—临高区域,图9展示了两种随机森林模型中贡献最大的前10个要素情况.从图9中可以看出,贡献最大的前10要素是相同的,但是每个要素的贡献程度会随着模型的变化而有所区别.在统一订正模型中,海口站点和临高站点贡献位于前四位的要素排序分别是:地表2米温度、最低气温(过去第一小时),最高气温(过去第一小时)以及950 kPa温度,其从高到低影响订正效果.但是在本文所提的模型中,海口站点位于前四位的要素却分别是:地表2米温度,950 kPa温度、最高气温(过去第一小时)以及最低气温(过去第一小时),而临高站点的前四位要素则与统一模型的前四位要素相同,这表明采用时空独立的随机森林模型可以反映出不同站点的区别,可以挑选出更具有特异性的要素组合,实现高精度的订正效果.同理,乐东—五指山、琼海—万宁两个局部区域也存在类似的现象,其贡献最大的前10位要素如图10所示.
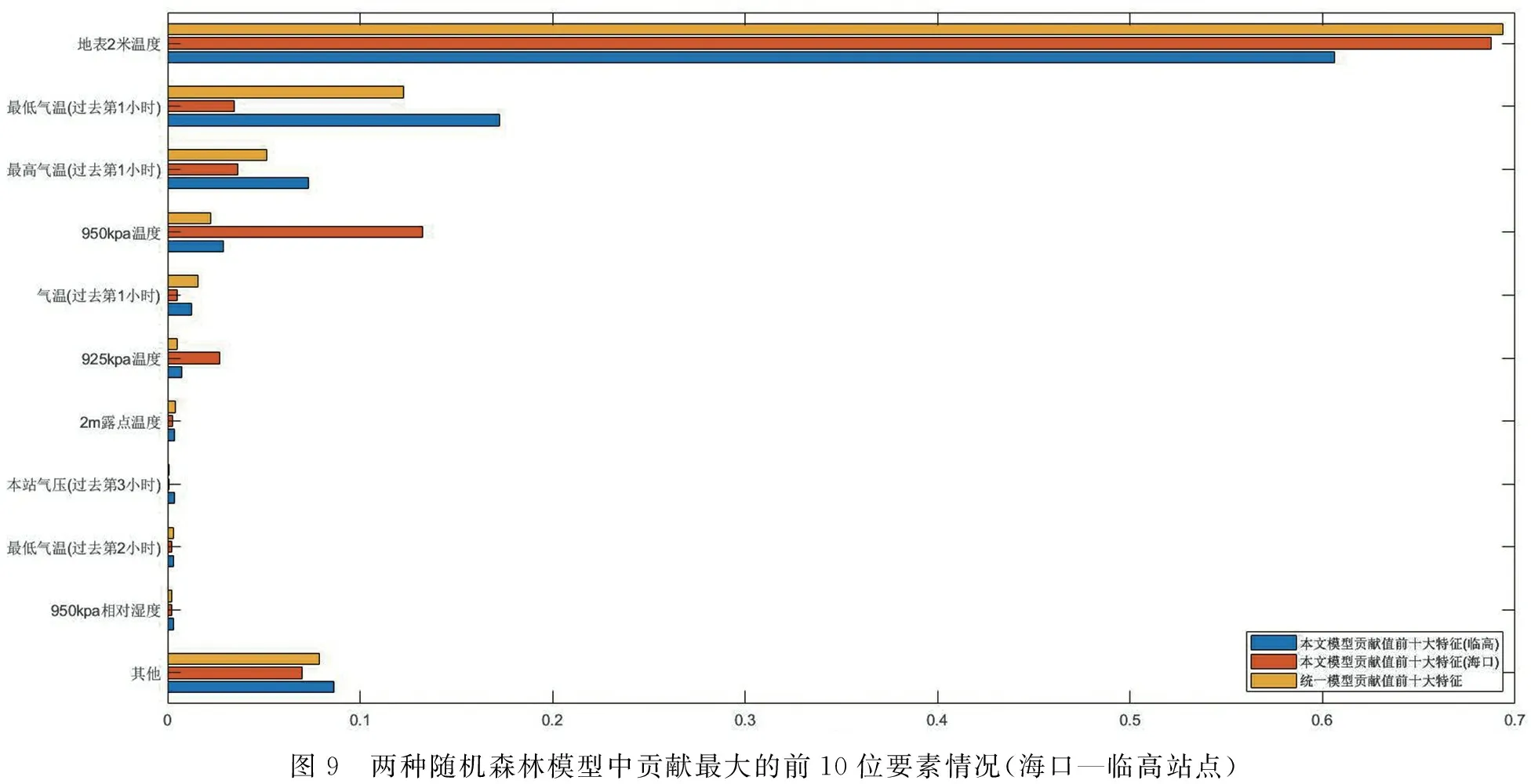
图9 两种随机森林模型中贡献最大的前10位要素情况(海口—临高站点)

a) 乐东—五指山b) 琼海—万宁图10 两种随机森林模型中贡献最大的前10位要素情况
4 结 论
本文提出了基于时空独立的随机森林模型对海南岛气温进行订正的方法,较之于采用统一随机森林模型进行订正的方法,本方法更能够充分考虑海南岛独特的热带区域以及地理地貌的气象多样性,能够分站点分时段地进行单独订正.结果表明,本文所提的方法不论是在单站点,还是在整个海南岛区域,它都明显优于ECWMF的预报结果,而且比统一随机森林模型的订正效果更加优越,能够实现对全岛范围气温的精准订正.此外,从各个要素的影响分析结果可知,基于时空独立的随机森林模型能够根据不同站点组合不同要素,而统一模型无法实现此效果,这也是本文中的模型优于统一模型的原因,此结果有助于加深对以往气温预测物理模型所使用的气象要素组合的认识.

