带加性噪声的随机波动方程的惯性流形逼近
李 琴,陈光淦
1. 四川师范大学 数学科学学院/可视化计算与虚拟现实四川省重点实验室,成都 610068; 2. 四川省江油中学,四川 江油 621700
波动方程是最重要的数学物理方程之一,它是关于时间的二阶偏微分方程,描述了振动在介质中的传播,在光波、声波和水波等自然现象中被广泛研究.惯性流形和稳定流形等不变流形刻画了系统动力学特征和有效行为.文献[1]证明了随机波动方程不变流形的存在性:文献[2]研究了随机波动方程的惯性流形的存在性.
本文考虑带加性白噪声的随机波动方程
u(0,x)=u0(x),ut(0,x)=u1(x),u(t,0)=u(t,π)=0
(1)
其中:ν>0,D=[0,π],W(t)是双边的L2(D)值的Q-维纳过程,其协方差算子Q满足trQ<∞.假设非线性项f在L2(D)上是全局Lipschitz连续的,并且Lipschitz常数是Lf.
由于维纳过程W(t)处处连续,处处不可导,文献[3-4]从数值模拟与计算角度研究了随机微分方程的逼近:文献[5]用光滑的Φε(t)去近似不光滑的W(t),得到随机微分方程的刻画:文献[6]通过一类平稳过程研究了Wong-Zakai型的近似.
考虑近似随机系统
(2)
1 预备知识

其中Lf为Lipschitz常数.
令
其中I为恒等算子.
方程(1)等价于下面的方程组
(3)
其中(u,v)Τ∈E.
方程(2)等价于下面的方程组
(4)

设
由ek的正交性,容易验证E1⊥E22,E-1⊥E22.再由文献[8]可知,在E11和E22上定义新内积
有E1⊥E-1,那么E1⊥E2.显然,E1⊕E2=E.那么算子A满足下面条件(指数二分性):
‖eAtP1x‖E≤Keαt‖x‖E,t≤0
‖eAtP2x‖E≤Keβt‖x‖E,t≥0
(5)
其中β<α<0,K>0,I=P1+P2.记E1=P1E和E2=P2E.
定义1设(Ω,F,P)是一个完备概率空间,θ={θt}t∈R是Ω上的变换族,定义映射

如果映射θt满足如下条件
则称(Ω,F,P,θ)为驱动动力系统.
定义2设(H,dH)是一个完备度量空间,如果映射

满足下面性质
φ(0,ω,x)=x
φ(t+τ,ω,x)=φ(t,θtω,φ(t,ω,x)),τ∈R,ω∈Ω,x∈H
则称θ和φ构成的二元组(θ,φ)为一个随机动力系统.
定义3对于随机动力系统φ(t,ω,x),如果对任意的t≥0,ω∈Ω,有
φ(t,ω,M(ω))⊂M(θtω)
那么随机集M(ω)称为正不变集.

考虑一个Langevin方程
(6)

它具有轨道不变性和测度不变性[9].定义


由文献[10]知,(u*(ω),v*(ω))Τ和(X*(ω),Y*(ω))Τ分别是下面线性方程组的唯一稳态解
(7)
(8)
实际上
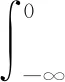
(9)

(10)
存在且分别生成下面的稳态解

(11)

(12)
定义如下非线性函数
那么gi(i=1,2)与f有相同的Lipschitz常数.
考虑下面的方程组
(13)
(14)
引入变换
T(ω,(u,v)Τ)=(u,v)Τ-(u*(ω),v*(ω))Τ
T-1(ω,(u,v)Τ)=(u,v)Τ+(u*(ω),v*(ω))Τ
Tε(ω,(Xε,Yε)Τ)=(Xε,Yε)Τ-(X*(ω),Y*(ω))Τ
T-1,ε(ω,(Xε,Yε)Τ)=(Xε,Yε)Τ+(X*(ω),Y*(ω))Τ

和
是随机动力系统,对任意(u,v)Τ∈E和(Xε,Yε)Τ∈E,过程

和

分别是(3)式和(4)式的解.
2 惯性流形的Wong-Zakai型逼近
和
定义Banach空间
其范数为
引理3[2]如果Lf满足
(15)
那么方程组(13)有不变的Lipschitz流形
ME(ω)={(ξ,h(ξ,ω))|ξ∈E1}


进一步,如果
(16)
那么ME(ω)是方程组(13)的随机惯性流形,其中Lh为h(ξ,ω)的Lipschitz常数.
用文献[2]中类似的方法可得到方程组(14)的惯性流形如下.
引理4[2]如果Lf满足(15)式,那么方程组(14)有不变的Lipschitz流形
MEε(ω)={(ξ,hε(ξ,ω))|ξ∈E1}


进一步,如果(16)式成立,那么MEε(ω)是方程组(14)的随机惯性流形.

(17)

(18)
(19)
对应的随机惯性流形的Lispchitz映射为
(20)
相应地,对(Xε,Yε)Τ作如下变换
(21)

(22)
(23)
对应的随机惯性流形的Lispchitz 映射为
(24)

证由方程组(11)和(12)有
(25)
记不等式(25)的最后一个不等号后的两个加式分别为I1,I2.对I1,由分部积分得
(26)

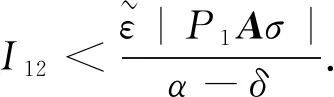

证由(19)和(23)式,有
(27)
在(27)式不符项中同乘e-ηt,有
那么
而
所以
由引理4,可得
因此


证首先当ε→0时由惯性流形映射(24)和(20)式,有


