Laws of 4D Printing

Farhang Momeni*, Jun Ni

Department of Mechanical Engineering, University of Michigan, Ann Arbor, MI 48109, USA

Keywords:Manufacturing Stimuli-responsive materials Mechanics of materials Time constant 4D printing

A B S T R A C T Three-dimensional (3D) printing is an additive manufacturing process. Accordingly, four-dimensional(4D) printing is a manufacturing process that involves multiple research fields. 4D printing conserves the general attributes of 3D printing (such as material waste reduction, and elimination of molds, dies,and machining)and further enables the fourth dimension of products to provide intelligent behavior over time. This intelligent behavior is encoded (usually by an inverse mathematical problem) into stimuliresponsive multi-materials during printing,and is enabled by stimuli after printing.The main difference between 3D- and 4D-printed structures is the presence of one additional dimension, which provides for smart evolution over time. However, currently there is no general formula for modeling and predicting this additional dimension. Herein, by starting from fundamentals, we derive and validate a general bi-exponential formula with a particular format that can model the time-dependent behavior of nearly all 4D (hydro-, photochemical-, photothermal-, solvent-, pH-, moisture-, electrochemical-,electrothermal-, ultrasound-, etc. responsive) structures. We show that two types of time constants are needed to capture the correct time-dependent behavior of 4D multi-materials.We introduce the concept of mismatch-driven stress at the interface of active and passive materials in 4D multi-material structures,leading to one of the two time constants. We develop and extract the other time constant from our unified model of time-dependent behavior of nearly all stimuli-responsive materials. Our results starting from the most fundamental concepts and ending with governing equations can serve as general design principles for future research in the field of 4D printing, where time-dependent behaviors should be properly understood, modeled, and predicted.

1. Introduction

Four-dimensional (4D) printing [1-7] is a manufacturing process that utilizes stimuli-responsive (smart) materials [8-10],mathematics, and additive manufacturing (AM). These three elements yield an encoded static smart structure that becomes a dynamic smart structure under the right stimulus through an interaction mechanism. 4D printing technology combines materials science and mathematics[11].In 4D printing,in addition to smart materials and AM, mathematical models are further needed for accurately predicting shape-morphing behaviors over time [6,12]. In simpler cases, these models may not be necessary.

The structures obtained by 4D printing technology are 4D space-time dependent [6,13-15]. The time-dependent behavior of 4D-printed structures relies on the special spatial arrangement between active and passive materials in the three-dimensional(3D) space (encoded by printing). Therefore, the fourth dimension in 4D printing indicates predictable and desired evolution over time that depends on 3D space, and this 3D space is the specific arrangement of (physical) voxels determined by mathematics and realized by printing. Prior to 4D printing, researchers did not typically try to generate a specific printing path (mainly by an inverse mathematical problem)to obtain a predictable and desired evolution over time. 4D-printed products and structures have unique advantages, some of which are discussed here:

1.1. Why 4D printing?

Using 4D printing, programming is performed at the material level[1,3].Sensing and actuation are directly embedded into materials [3]. Random (free) energy is used to construct non-random structures [1]. Self-assembly is performed at the macro scale to eliminate post-fabrication assembly [3]. Buildings can be selfassembled on Mars [16]. The number of parts in a product is reduced [3]. Volume in shipping is reduced using 4D structures that are activated on-site[2].The number of failure-prone components used in conventional robots and electromechanical systems is minimized [3]. 4D printing can be used for embedding bioinspired morphing features into materials [15]. More advantages can be mentioned for 4D printing in various fields.

1.2. Why 4D by printing?

First, the same reasons that motivate us to use AM instead of other manufacturing processes for conventional materials motivate us to use AM for smart materials.Some of these reasons are as follows:Molds and dies are eliminated,material waste is reduced,and complex geometries are obtained. Second, using printing, we can elaborate on (i.e., manipulate) the ‘‘internal structures” of multimaterials. In other words, 4D ‘‘printing” enables local anisotropy to be encoded [5]. This is uniquely important in 4D printing for obtaining various shape-morphing behaviors. Encoding the structures of materials is not achievable (or hardly achieved) by other manufacturing processes. As one example, bioengineers are primarily motivated to produce tissues and organs through bioprinting because a proper function of an organ depends on its internal structure, in which various cells are contained in a complex architecture and multi-scale vasculature [17]. Systematic yet local elaboration on the internal structure is not easily achieved by other fabrication processes. For instance, bioengineers do not use bioinjection molding or other methods to mimic biological structures that have highly complicated internal architectures.

Following this Technology, Entertainment, Design (TED) talk in 2013 that introduced 4D printing[1],Tibbits[2]published a paper on 4D printing entitled ‘‘4D printing: multi-material shape change.” Truby and Lewis [18], in their references section, indicated that the aforementioned paper by Tibbits [2] ‘‘describes the first embodiment of 4D printing.” Note the word ‘‘multimaterial” in the title of the work done by Tibbits [2]. This word has been used to introduce 4D printing. Although some studies have demonstrated single-material 4D-printed structures, the future of 4D printing resides in multi-material structures [2,19-29]. Most current researchers consider 4D printing in a multimaterial fashion using smart(active)materials that are selectively arranged with conventional(passive)materials to obtain desirable shape-shifting behavior[22].Utilizing a single(active)material for the entire 4D structure has been less considered [22]. The physics of 4D-printed structures usually requires the use of multimaterials [20]. A well-balanced 4D-printed component is intrinsically a multi-material structure[23].In the most fundamental case,a multi-material 4D-printed structure has one active and one passive layer [21]. Performance improvement by allocating proper materials to related locations based on local necessities [30],multi-functionality by embeddable functions such as electronics[31], combining rigid and flexible sections in an integrated structure [32], and providing lightweight structures [33] are only some of the advantages of multi-material structures.Moreover,to enable the shape memory effect (SME) (which is not an intrinsic property of shape memory polymers (SMPs) [10]), a mechanical force is required in addition to heat (thermomechanical cycles).This force is usually provided externally by human intervention in single-material SMPs.However,4D printing can help us arrange active and passive materials in a multi-material structure and utilize their internal mismatch-driven forces to enable the SME autonomously without requiring an external load (i.e., human intervention) for training [34,35]. Furthermore, combining SMPs with a passive layer (multi-material structure) can be one of the simplest means of producing reversible (two-way) SMPs [36-41].For these reasons,multi-material structures have received growing attention in 4D printing. This means that when researchers perform general research on 4D printing, they typically elaborate on the active-passive combination (multi-materials) [21-24,42-46].In 4D printing, it is best to arrange active and passive materials to obtain self-sensing and self-actuating operations,as no conventional sensors or actuators are used to enable predictable and complex shape-shifting behaviors. Self-sensing can be achieved by using active (smart) materials, and self-actuating can be achieved by arranging active and passive materials to generate some mismatch-driven forces and guide these self-actuation forces in the desired direction(as derived from mathematics).Nevertheless,the results of this study can be useful for both single-material(active) and multi-material (active-passive) structures, as discussed in a remark later in this article.

Various aspects of 4D printing have been explored in the literature. Several studies have considered beam and plate theories (e.g., see the supplementary information provided in Ref.[5]). However, no study has considered a general modeling of‘‘time-dependent” behaviors (the fourth dimension) of 4D structures. Time-dependent behaviors are critical aspects of 4D(stimuli-responsive) materials, whether such materials are fabricated by printing (and thus called 4D-printed structures) or produced by other manufacturing processes. More importantly,numerous studies on 4D materials have used the Timoshenko bimetal model [47], which is linear with time, to analyze the time-dependent behaviors of their experiments. In this study, we observe that the Timoshenko bimetal model cannot capture the true time-dependent behaviors of 4D materials (except in some special cases or selected linear regions), although it does provide useful insights into time-independent behaviors, as many studies have correctly used the Timoshenko bimetal model for analyzing time-independent behaviors such as the effect of thickness on bending. In fact, the purpose of the Timoshenko bimetal model is not to model the time-dependent behaviors(the fourth dimension)of 4D materials.Therefore,an urgent need exists for qualitative and quantitative analyses of the fourth dimension of 4D materials.Some of the different formulas used or developed for modeling the shape-morphing behaviors of 4D-printed structures are organized and analyzed in Table 1 [5,20,21,37,48-60].

Now, we provide a discussion about Table 1:

(1) The formulas used or developed in 4D printing for the modeling of the shape-morphing behaviors can be divided into five categories: ①pure geometry, ②customized and case-specific models, ③Euler-Bernoulli model, ④Timoshenko bimetal model,and ⑤extension of each of these models to plates (e.g., spherical and saddle-like structures), for which two curvatures are used(usually the mean and Gaussian curvatures, which are functions of the two principal curvatures). This is not a strict classification,but is instead for general understanding.

(2) Some studies have modeled the shape-morphing behaviors of 4D materials based purely on geometry.These models are basic and usually must directly measure one of the key parameters related to the shape,such as the curvature radius or bending angle.Therefore, these models cannot be used as standalone models for predicting shape-morphing behaviors.

(3) Some studies have developed customized models for their specific cases (e.g., [21,51]). These models are not typically used for general purposes and may not consider all of the important parameters.

(4)Several studies have directly used the Euler-Bernoulli model or customized it for their specific cases.

(5) Most studies have directly used the Timoshenko model(more specifically, the Timoshenko bimetal model [47]) or customized it for their specific cases. In addition, some studies have used Timoshenko (and Euler-Bernoulli) model without mentioning the name or work of Timoshenko (and Euler-Bernoulli).

(6) Finally, each of these categories can be extended to plates.One example that extended the Timoshenko bimetal model to 2Dhas been previously mentioned [5] (and more references could be cited for each of the aforementioned categories,particularly for the Timoshenko and Euler-Bernoulli models).

Table 1 Different formulas used or developed in 4D printing for modeling shape-morphing behaviors.

Table 1 (continued)

(7)The models that are based on pure geometry are a subset of all other categories.For example,Refs.[21,51]also used geometrical relationships in their derivations, in which they assumed that the energy generated in the contraction of the active layer would lead to the deformation of the passive layer. Those geometrical relationships are also intrinsically considered in the Euler-Bernoulli and Timoshenko models.

(8) Timoshenko’s theory is an improved and advanced version of the Euler-Bernoulli theory. The Timoshenko bimetal model is an even more advanced and relevant version.

(9) Even though most of the studies in 4D materials used the Timoshenko bimetal model, those based on pure geometry or the Euler-Bernoulli model can be regarded as a subset of the Timoshenko bimetal model. In addition, the customized(case-specific) models are not general and may also ignore some important parameters.

(10) Three main points can be summarized as follows: ①No general formula exists for properly modeling the time-dependent behaviors and that is suitable for various stimuli and materials;②the Timoshenko bimetal model [47] seems to be the most trusted formula in 4D materials (mainly for modeling timeindependent behaviors); and ③in our study, we consider the Timoshenko bimetal bimetal model[47]mainly for the initial step(i.e., the equilibrium (balances of forces and moments) and compatibility conditions). The Timoshenko bimetal model cannot capture the time-dependent behavior of various 4D materials. We introduce and embed ‘‘time” into the Timoshenko bimetal model systematically and in detail.

The main aspect of 4D-printed structures is the fourth dimension. However, no general formula currently exists for modeling and predicting this additional dimension. Here, by developing fundamental concepts and starting from the equilibrium and compatibility conditions, we derive a necessary bi-exponential formula for modeling and predicting the fourth dimension of any multi-material 4D-printed structure. We further validate our bi-exponential formula using various experimental data from previous independent studies and show that it is a general formula useful for various 4D (e.g., photochemical-, photothermal-,solvent-, moisture-, heat-, and ultrasound-responsive) multimaterial structures. This generality is observed (when analyzing various experimental data) because we build the bases of our biexponential formula comprehensively.

2. Definitions, derivations, and discussions

The time-dependent behavior (i.e., fourth dimension) of any 4D-printed structure must be predicted. A detailed but systematic study on 4D printing and related areas enables us to identify three general laws that govern the shape-morphing behaviors of nearly all 4D structures, even though many materials and stimuli exist(Fig. 1). The purposes of these laws are first, to understand, and second, to model and predict the fourth dimension.

2.1. First law of 4D printing

Nearly all shape-morphing behaviors (e.g., photochemical-,photothermal-, solvent-, pH-, moisture-, electrochemical-,electrothermal-, ultrasound-, enzyme-, hydro-, and thermoresponsivity) of multi-material 4D-printed structures originate from one fundamental phenomenon,which is‘‘relative expansion”between active and passive materials.

This ‘‘relative expansion” is the origin of nearly all complicated 4D printing shape-morphing behaviors such as twisting, coiling,and curling, which are enabled by encoding various types of anisotropy between active and passive materials and fabricating different heterogeneous structures.

2.2. Second law of 4D printing

The shape-morphing behaviors of nearly all multi-material 4D-printed structures have four types of physics: mass diffusion,thermal expansion,molecular transformation,and organic growth,which are discussed,quantified,and unified in the subsections that follow.

All of them lead to the relative expansion between active and passive materials and consequent shape-morphing behaviors under stimuli. The stimulus is usually provided externally, but it can be internal.

We quantify all four categories of the second law in terms of strain. One reason for this can be given by the following example:If we want to quantify the categories in terms of mass,then we do not have any mass change in the next category (thermal expansion). Similarly, we do not have temperature change in this category, whereas we do have it in the next category.

In this category, several stimuli and mechanisms can be used,including hydro-, solvent-, moisture-, pH-, enzyme-,photochemical-, and electrochemical-responsive mechanisms. All of these stimuli ultimately cause a matter transport,leading to relative expansion in multi-material 4D structures and resulting in various shape-morphing behaviors. It should be noted that these stimuli are some examples that can cause a matter transport.However, some of them are not unique to this category. The type of material and the interaction between the material and stimulus are important. For example, in the solid state, a photochemicalresponsive mechanism can lead to a shape-morphing behavior without any mass change. In this example, the photochemicalresponsive mechanism causes a molecular transformation (the third category).

2.2.1.2. Thermal expansion. In this category, a temperature change will increase (or decrease) the average distances between atoms and molecules(with constant mass), leading to relative expansion in multi-materials.

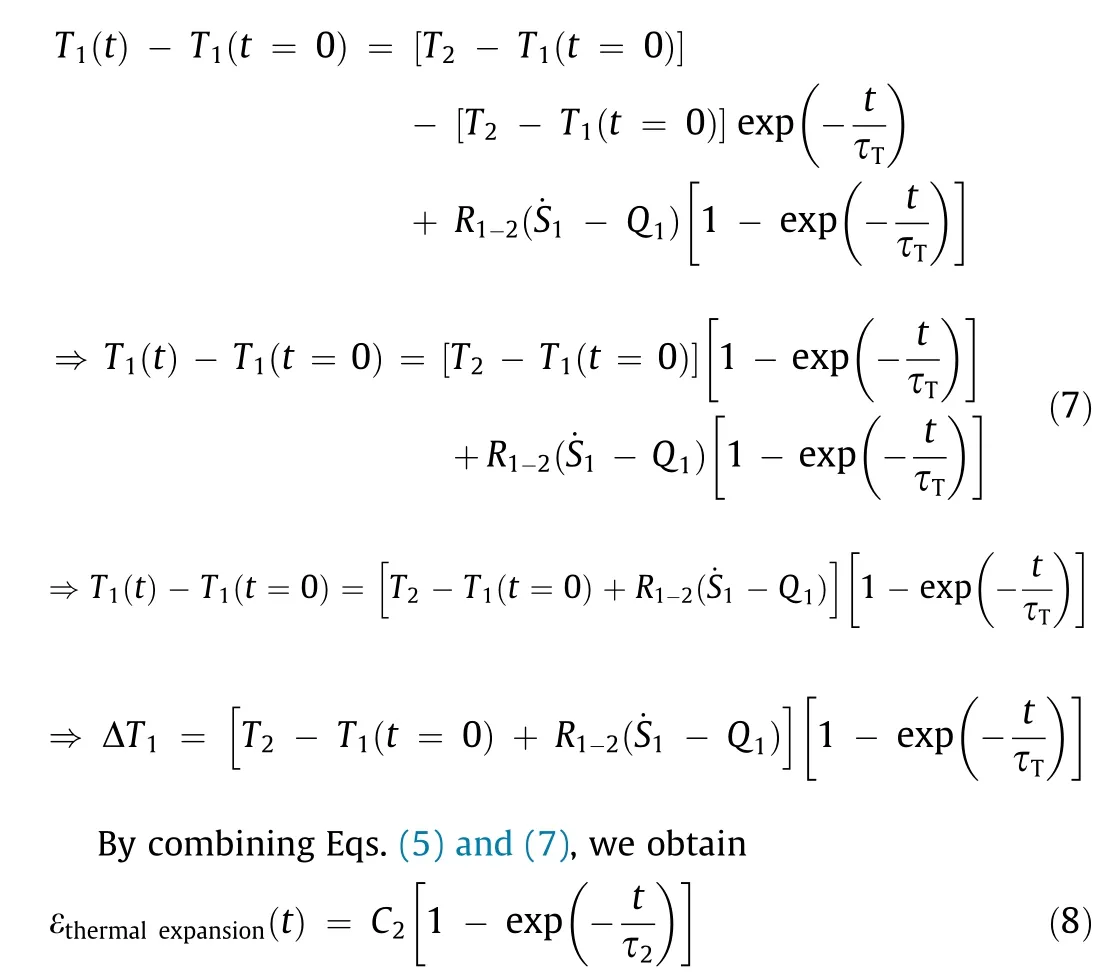
where C2and τ2are constants that depend on the previous parameters. In this category, several stimuli and mechanisms can be used, including photothermal-, electrothermal-, and ultrasound-responsive mechanisms. All of these stimuli ultimately raise the temperature of the structure and consequently increase the average distances between atoms and molecules. For example, in electrothermal-responsive structures, the movement of a current through a resistance provides heat (so-called Joule or Ohmic heating). This heat increases the temperature, ultimately leading to expansion. Similarly, contraction is obtained by cooling. It should be noted that some materials will shrink (contract)upon heating. In these cases, α would be negative in the previous equations, and the form of the final equation (i.e., Eq. (8)) will remain intact.

2.2.1.3. Molecular transformation. In this category, a molecular transformation with constant mass and temperature leads to relative expansion. The molecular transformation in the structure can be triggered by an electric field, magnetic field, light, mechanical force, etc. For example, by applying an electric or magnetic field to appropriate materials, dipoles in the material will be aligned along the field, leading to a shape change; or by applying an ultraviolet (UV) light to a photostrictive material, as a result of trans-to-cis conversions, a shape change will occur. Similarly,by applying a mechanical tension to a polymer, the chains will be aligned along the force direction, resulting in a shape change.Regardless of the type of stimuli, these phenomena have some common features. First, these molecular transformations usually start from a randomly or differently oriented condition. Second,they require time to be fully realized.Third,they have a saturation limit(e.g.,when all dipoles align,all trans-to-cis conversions occur,or all chains align). Based on the original definition of the derivative,

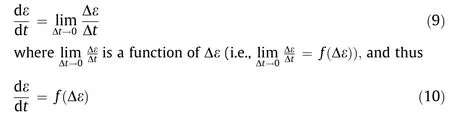
The strain ε ＝ΔL/L and thus Δε are generally small numbers(this is a logical assumption, otherwise the stress-strain relationship becomes nonlinear). We approximate the function f （Δ ε）around Δε ＝0 using the Taylor series as follows:

This behavior is observed, for example, when: ①An electric field moves the charged regions in the related materials, leading to a strain[67];②a magnetic field moves the magnetized regions in the relevant materials,resulting in a strain[66];③a light source causes photochemical conversions (that are different from a photothermal mechanism) in the appropriate materials, leading to a strain [68,69]; or ④an external pressure moves polymer chains, thus producing a strain [70]. In all of these mechanisms, a molecular transformation with constant mass and temperature leads to a shape-morphing behavior. Therefore,

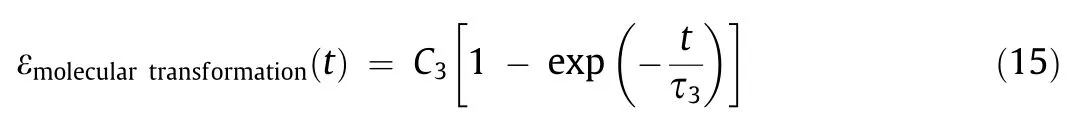
where C3and τ3are constants that should be modeled in a specific application based on the type and characteristics of the stimulus as well as material properties. For example, in a photochemicalresponsive mechanism,in crystals,C3and τ3depend on the irradiation flux intensity, quantum yield of the transformation, and other factors, and can be modeled in a specific case [69]. We introduced the constant-temperature feature in this category to indicate that the relative expansion of this category is not due to thermal expansion/contraction, even though some thermal fluctuation may occur in the structure due to bond cleavage or formation.In this category,various stimuli and mechanisms can be used as previously discussed.

2.2.1.4. Organic growth. In this category, a living layer (organism)exists and its growth over time can lead to relative expansion between active and passive materials. The organic growth can be defined as the increase in the weight or length of an organic system[71]. This usually occurs in areas of bioscience and bioengineering dealing with, for example, cells, soft tissues, organs, and scaffolds,which can be 4D printed; these are generally referred to as 4D bioprinting.

Kinetics of the organic growth is [71]

where C4and τ4are constants that depend on the previous parameters.In this category,one of the main stimuli that can trigger a living organism is the electrical signal (electrochemical mechanism). In addition, various stimuli such as pH, light, heat,and enzymes can be used to tune the growth rate.

2.2.2. Unified model of the second law

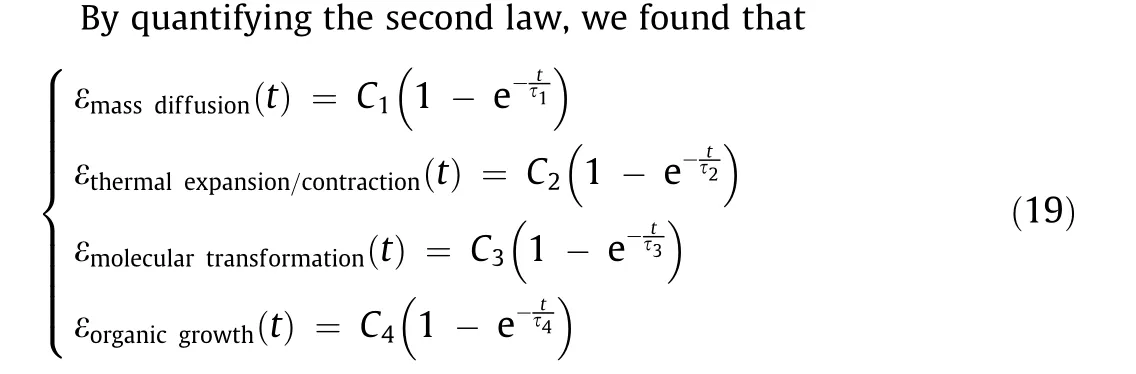
where Cjand τj（j ＝1， 2， 3， 4） are all constants. However, they depend on different factors as previously described.

2.3. Third law of 4D printing

Time-dependent shape-morphing behavior of nearly all multimaterial 4D-printed structures is governed by two‘‘types” of time constants. For the most fundamental case of a multi-material 4Dprinted structure having one active and one passive layer (Fig. 2),the time-dependent behavior (in terms of ‘‘curvature,” which is a building block concept for shape-morphing behavior) is

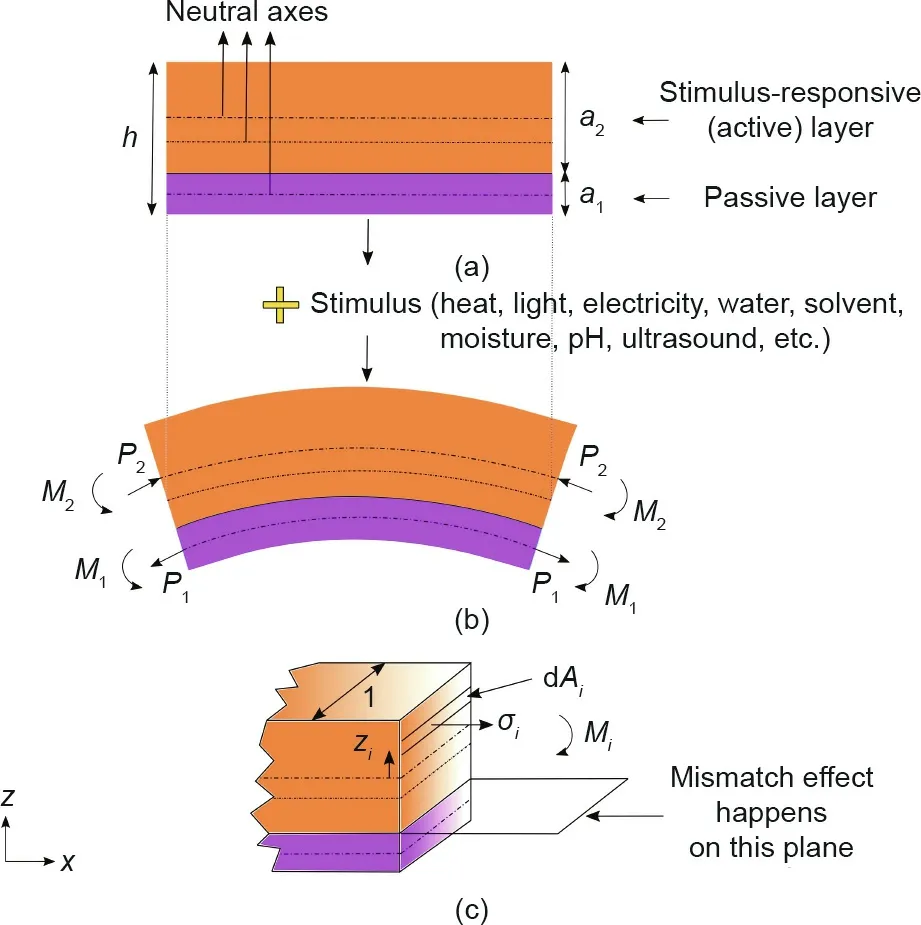
Fig.2. Toward the third law by analyzing the most fundamental multi-material 4D structure. (a) Before applying a stimulus; (b) after applying a stimulus; (c) crosssectional view of an element of the bilayer after applying a stimulus. The passive and active layers are denoted by numbers 1 and 2, respectively. P1: force in the passive layer; P2: force in the active layer; M1: moment in the passive layer; M2:moment in the active layer;Ai:cross-sectional area of the active or passive layer;zi:distance from the neutral axis of the active or passive layer;σi:stress in the active or passive layer.

2.3.1. Proof of the third law

To derive Eq.(20),we start from the equilibrium and compatibility conditions that are the starting point for any related problem in mechanics of materials[64].We also consider the Timoshenko bimetal model [47] and its basic assumptions. We consider the Timoshenko bimetal model mainly for the initial step of the equilibrium(balances of forces and moments)and compatibility conditions.

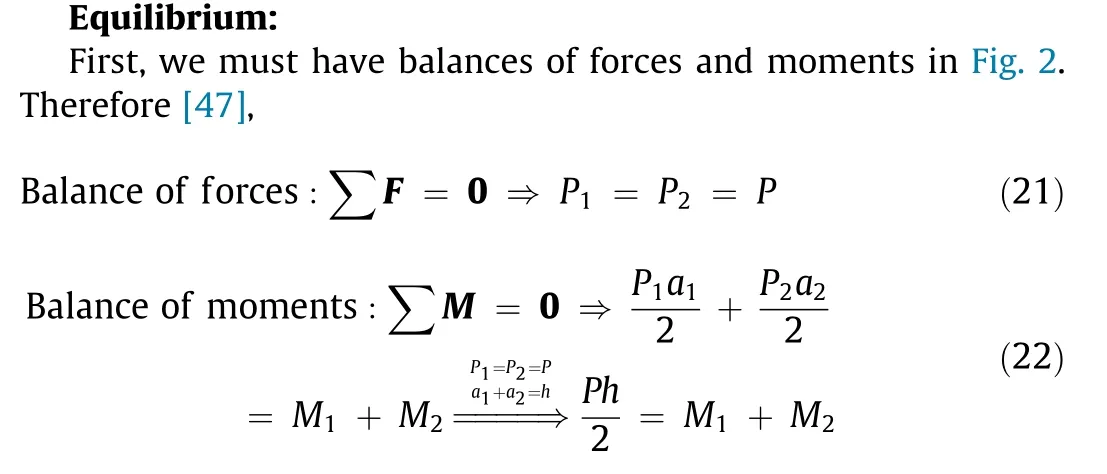
where P1and P2are forces; M1and M2are moments (as shown in Fig. 2).

Compatibility:

Second,at the interface of the two layers,the lengths of the two layers are the same after the stimulus has been applied. Because their initial lengths are also the same, their strains must be equal and thus [47,64],

where Mmis moment due to the mismatch-driven stress. The first terms on the right-hand side of Eq. (29) are similar to those proposed by Timoshenko [47], and the second terms (Mm1and Mm2)are introduced in this study. At this stage, Mm1and Mm2are moments. Let us retain them as black-box terms.

where G1and G2are constants that depend on Young’s moduli of the active and passive layers and the amount of the mismatchdriven stress generated at the interface. This stress is affected by the stimulus power (light intensity, pH value, etc.). B1and B2are time constants that depend on the viscosity induced at the interface(which is related to the active-passive composite) and Young’s moduli of the active and passive layers. It should be noted that Young’s modulus and viscosity are affected by the fabrication process[35]and its conditions,such as printing speed and printing resolution. In general, some of the properties of materials are affected by the printing conditions.

In addition,because the two layers are attached at the interface during the shape-morphing behavior, B1and B2(time constants of strains in each layer due to the mismatch-driven stress at the interface) are equal (B1＝B2＝τI）. Thus,

2.3.2. Stimulus-on versus stimulus-off

Eq. (20) is used when the stimulus is ‘‘on” and a curvature occurs in the structure. However, when the stimulus is ‘‘off,” the structure can return to its original shape by starting from the final curvature of the previous part (i.e., the stimulus-on region).Therefore, the governing equation for the second region can be obtained as:

It should be noted that for materials that are intrinsically reversible, a self-locking mechanism can be devised by special arrangements of active and passive materials so that when the stimulus is off, the structure does not return to its original shape (if needed).

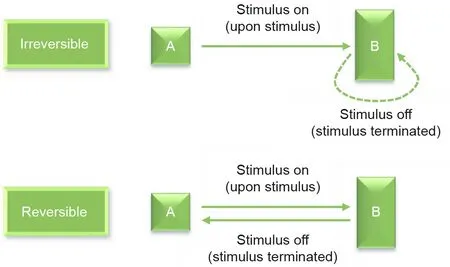
Fig.3. Irreversible(one-way)and reversible (two-way)shape-morphing behaviors[40,76,77].

2.3.3. General graph

Based on Eqs. (20) and (37), the general graph is rendered as Fig. 4.

2.3.4. Validation

Fig. 4. General graph exhibiting the time-dependent behavior of nearly all multimaterial 4D-printed(e.g.,photochemical-,photothermal-,solvent-,pH-,moisture-,electrochemical-, electrothermal-, ultrasound-, enzyme-, and hydro-responsive)structures. (a) One cycle; (b) multiple cycles. Some applications require only one cycle; others require multiple cycles. In some applications, only one of the two regions of the graph is present, and in other applications, both regions are present.In some cases,the shape-morphing behavior can occur with the SME;in other cases,it can occur without the SME. It should be noted that we may need to swap the labels of ‘‘stimulus on” and ‘‘stimulus off” on this graph in some cases.

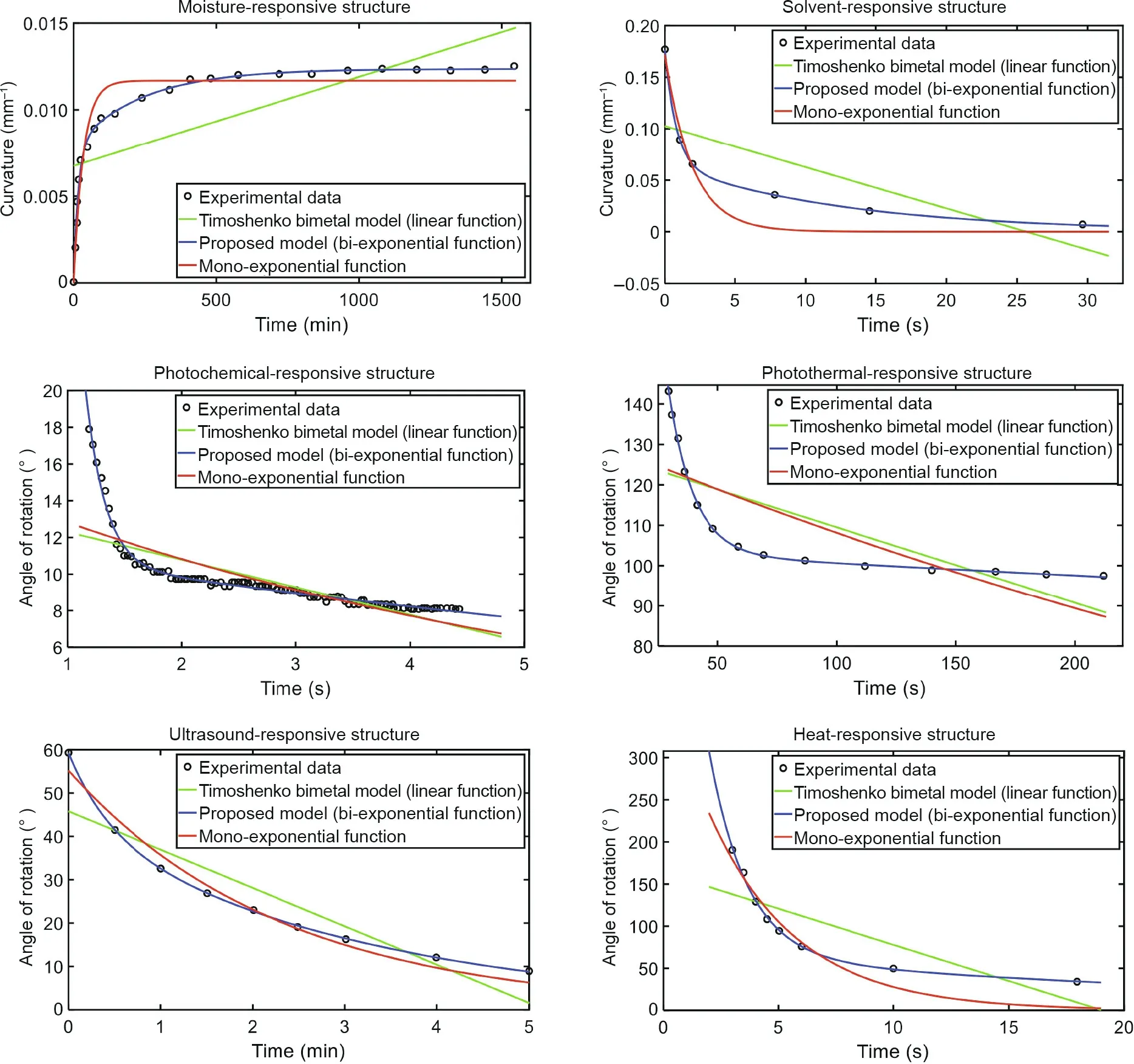
Fig.5. Validation of the proposed model by experimental data from independent studies in Refs.[37,80-84]for both on and off regions and various stimuli such as moisture[80], solvent [81], photochemical [82], photothermal [83], ultrasound [84], and heat [37]. We performed curve fitting using the Levenberg-Marquardt [85,86] method. We also applied other least-squares algorithms and obtained similar results.

Here, we validate our derived bi-exponential formula. For completeness, we also consider the Timoshenko bimetal [47]and mono-exponential models. As Fig. 5 [37,80-86] shows,unlike the Timoshenko bimetal and mono-exponential models,the developed bi-exponential model perfectly captures the correct time-dependent behavior of various experimental data from previous studies, where each research group is usually expert in one specific type of stimulus or smart material (e.g., moisture or electrochemical-responsive materials). Therefore, in general, the time-dependent behavior of 4D multi-materials is nonlinear(with time) and has the specific format as given in Eq. (20).Some of the previous studies referenced in Fig. 5 [37,80-86] presented experimental data for time-dependent curvature, whereas others provided experimental data for time-dependent angle of rotation (deflection angle). However, the curvature and deflection angle have a linear relationship. Consequently, if one of them exhibits bi-exponential behavior, the other will exhibit bi-exponential behavior. All six items shown in Fig. 5 [37,80-86] have one active and one passive material. The active component exhibits responsivity to the desired stimulus, whether with or without SME.

We will discuss a case study as follows. Here, we show a stepby-step example regarding the bi-exponential formula derived in the third law. We generate the time-dependent behavior of the heat-responsive structure shown in Fig. 5 [37,80-86] using our bi-exponential equation in a step-by-step procedure and compare the generated behavior with the experimental data (actual timedependent behavior) proposed in that study (i.e., Ref. [37]). The study in Ref. [37] used polylactic acid (PLA) strips of 60 mm× 0.8 mm × 0.12 mm (length × width × thickness) in a bilayer structure with the paper membrane(60 mm×0.8 mm×0.1 mm)and a heating plate with a temperature of 90 °C. The ambient temperature in those experiments was 20 °C. They used a digital camera by which they measured the angle between the normals of the composite strip ends. The physics of this bilayer structure resides in Category 2 of the second law (thermal expansion/contraction).

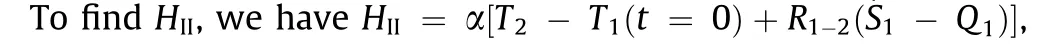
By using these values, we obtain Ra ＝2，which is less than 109,and thus the flow is laminar[65].Therefore,we use the Nusselt number formula related to laminar flow as given in Eq. (39). Furthermore, n1＝0.5. Consequently,Nu ＝1.6 and Rku＝363 K·W-1. Therefore, R1-2＝160 K·W-1and finally, τII≈1.6 s. We also model a case in which the composite strip is heated horizontally(rather than from the lateral side) so that the paper layer is between the heating plate and PLA layer. For this case, based on the physics of the new situation, we ignore the surface-convection heat transfer, but we consider the contact thermal resistance. A similar value of τIIis obtained.Nevertheless, the first modeling is appropriate because the composite strip is heated from its lateral side in the experiment in Ref. [37] related to the bending angle measurement.

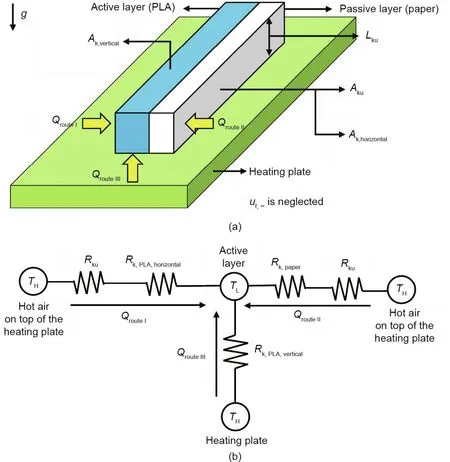
Fig. 6. Simplified thermal model of the case study. (a) Physical model; (b) thermal circuit model. g: gravitational acceleration constant; Ak,vertical: vertical conduction area;Ak,horizontal:horizontal conduction area;Aku:surface-convection area;Lku:surface-convection characteristic length;uf，∞:far-field fluid velocity;TH:high temperature;TL:low temperature; Rk: conduction thermal resistance; Rku: surface-convection thermal resistance; Q: transferred heat.

It should be noted that the simplified thermal model shown in Fig. 6 is not unique and can be somewhat different depending on the type and level of simplifying assumptions.

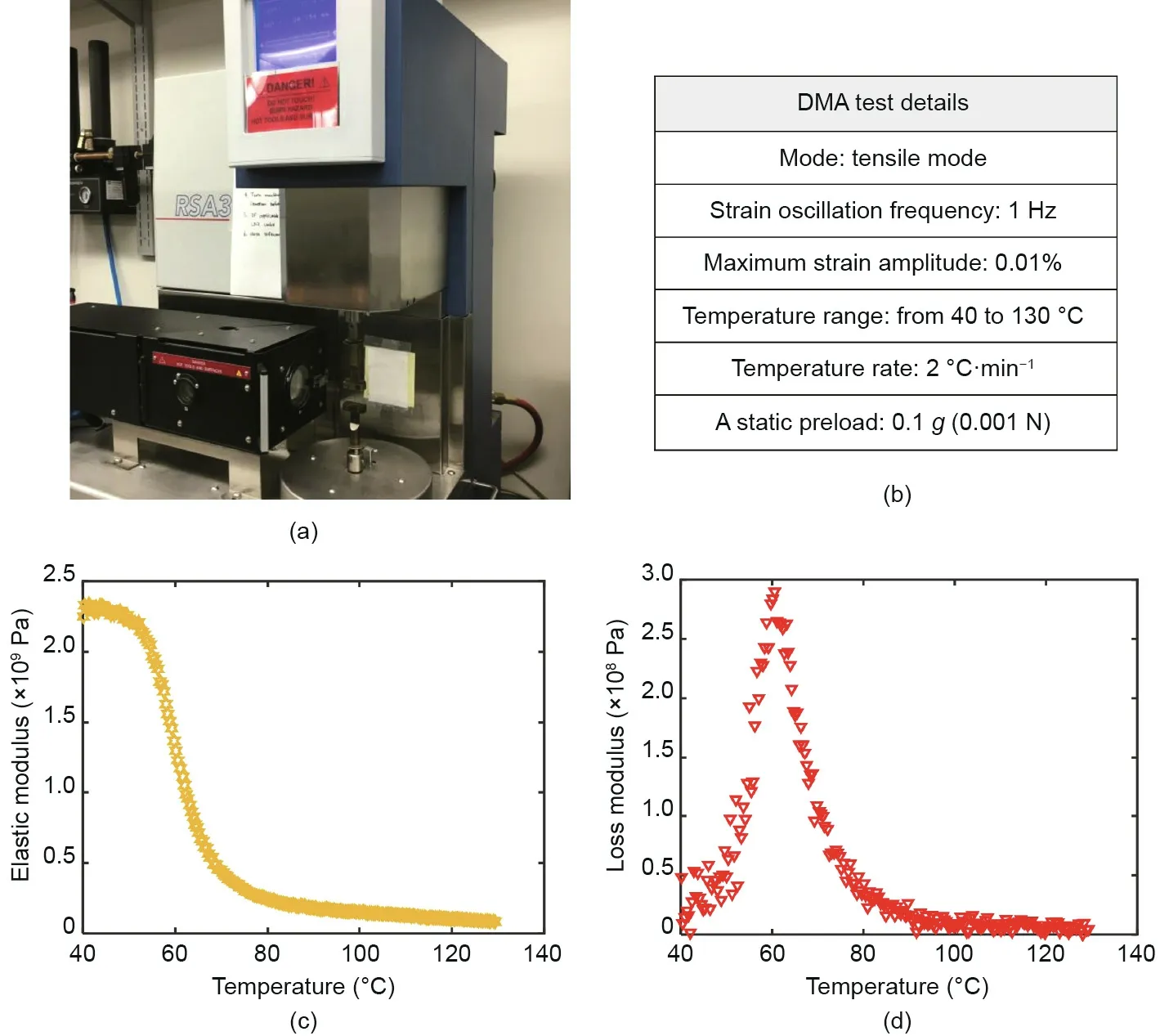
Fig. 7. DMA test. (a) DMA machine (RSA3, TA Instruments, USA); (b) test conditions; (c) storage (elastic) modulus; (d) loss modulus.

Table 2 Values of the parameters of our bi-exponential formula for a bilayer of PLA/paper composite.

We presented three laws.Laws are different from theories.Law is the starting point and reveals something that exists. By further analysis,laws can lead to theories.Theories are usually more complicated expressions. A step-by-step example analyzed here can provide a basis for future theories in 4D printing. These laws capture and show the big picture.Currently,different approaches may exist to find τI，τII, HI, and HIIin a specific case, but the final bi-exponential equation in terms of τI，τII, HI, and HIIwould be the same (Fig. 9). Future theories can examine more details of τI，τII, HI, and HIIto find some general models for each of them.

2.4. Remarks

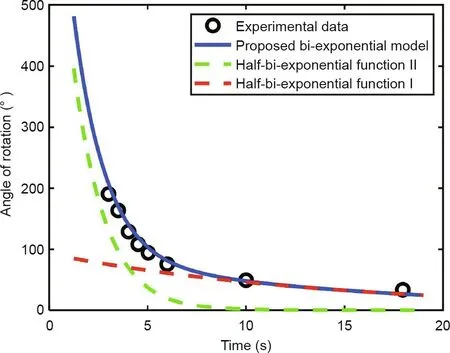
Fig.8. Comparison of theory and practice(experimental data from Ref.[37])in the case study.

By analyzing Eq. (41), we find that the curvature first increases and then decreases with an increase in a1.Because Eq.(41)is symmetric in terms of a1and a2,the curvature exhibits a similar trend with respect to a2. The region in which the increase or decrease of the curvature occurs depends on the relative values of a1and a2as well as E1and E2. In this article, we generate some possible scenarios as shown in Fig. 10. Because of the symmetry of Eq.(41),the same results as Figs.10(a)and(b)are valid if we swap a1and a2in these two plots.A similar result to the scenario shown in Fig. 10(c) was proposed by Timoshenko [47].

Remark 3.Shape-morphing speed.The shape-morphing speed is crucial in nearly any application performing dynamic intelligent behavior over time,and becomes critical in some applications such as autonomous deployment in space missions, drug delivery systems, and detection devices. Through derivatives of Eqs. (20) and(37), the magnitude of the shape-morphing speed for both on and off regions would be

As seen in Eq. (42), the shape-morphing speed is timedependent with the specific format shown. However, the Timoshenko bimetal model [47] gives a constant shape-morphing speed over time.

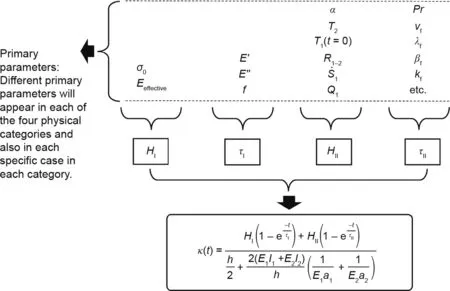
Fig. 9. Road map of parameters. The four physical categories as well as each specific case in each category will require different approaches to obtain HI, τI, HII, and τII.Therefore, different primary parameters will appear on the road toward the final general bi-exponential equation.

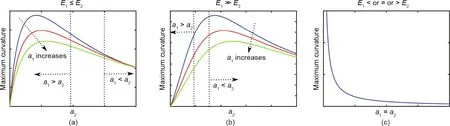
Fig. 10. Depending on the relative values of a1, a2, E1, and E2 （Eq.（41））, the relationship between curvature and layer thicknesses would be different (it can be decreasing,increasing,or a mixed behavior).(a)The relationship between curvature and thicknesses,when E1 ≤E2 and a1 ＞a2 or a1 ＜a2;(b)the relationship between curvature and thicknesses, when E1 ≫E2 and a1 ＞a2 or a1 ＜a2; (c) the relationship between curvature and thicknesses, when E1 ＜or ＝or ＞E2 and a1 ＝a2.

Based on Eq. (42), for a large amount of time (i.e., when the maximum curvature (final shape) is going to be achieved), the shape-morphing speed tends to zero for both the on and off regions. This point can also be captured from Fig. 4, where both the on and off regions become flat (constant) for t approaching large values, and the derivative of a constant function is zero.

Remark 4.Stimulus power.Here,we analyze the effect of stimulus power on the time-dependent behavior. By the expression‘‘stimulus power,”we mean light intensity,temperature magnitude,pH value, moisture content, enzyme concentration, current magnitude, solvent concentration, and so on. By analyzing the various parameters of Eq. (20) and considering the concepts associated with the second and third laws,we find that the stimulus power will affect three parameters, HI, HII, and τII. Therefore,the time-dependent behaviors related to two stimulus powers would be

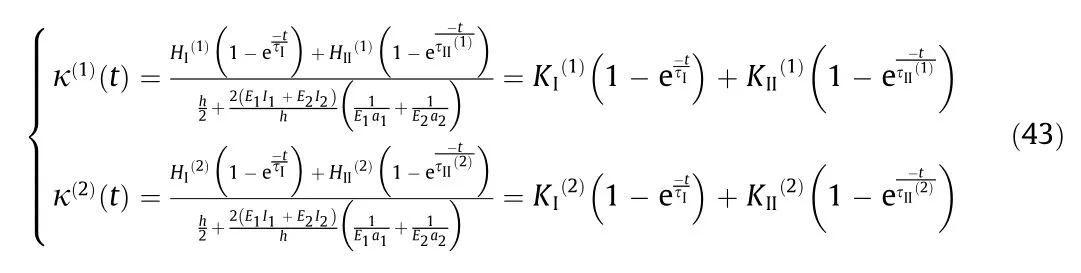
To illustrate the effect of stimulus power on time-dependent behaviors, we consider five stimulus powers.The related formulas would be

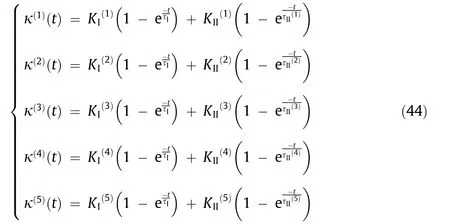
The general graph would be similar to Fig. 11(a). The general trend observed in Fig. 11(a) is consistent with the experimental data found in Refs. [82,83,92,93].

Some applications might exist in which a faster response without any change in the final(maximum)shape,unlike that shown in Fig.11(a),is desirable.To this end,a smaller time constant （τ ）with the same coefficient （K ） is required. For five scenarios, the related formulas would be

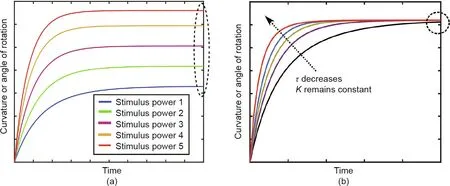
Fig. 11. (a) General effect of stimulus power (e.g., light intensity, pH value, and temperature magnitude) on the time-dependent behavior. This plot is based on Eq. (44);(b) tuning the response speed without changing the final shape (maximum curvature). This plot is based on Eq. (45).

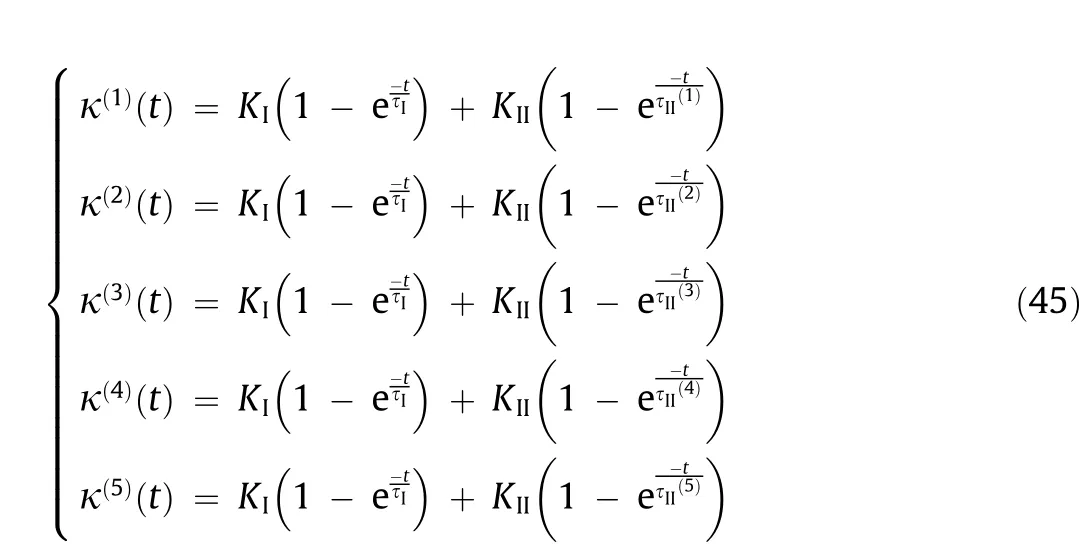
The general graph would be similar to Fig. 11(b). To tune the response speed without interfering with the final shape, separate studies are needed.Carbon nanotubes[94]may be a possible solution,as they can be incorporated into stimuli-responsive materials to tune their response speed [95].

Remark 5. Extension of the developed concepts to complicated multi-material 4D structures.Based on the concepts developed in this study,the time-dependent behaviors of multi-material 4D structures can be analyzed, predicted, and tuned at nearly any level of complexity. Let us consider one simple example exhibited in Fig. 12. This case has four types of materials, two of which are active materials.For the top two layers,we have exponential terms type I and type II. Similarly, we can consider the middle two and bottom two layers. When these terms are superposed, this multimaterial structure has three exponential terms of type I and three exponential terms of type II;nevertheless,some of these exponential terms can be equal or negligible in a specific case,as discussed in Remark 1.In addition,this case will have the same general graph shown in Fig.4,as its governing equation is a summation of exponential terms. However, the slope of its graph at a similar point would be different from that of the bi-exponential model.

To realize complicated 4D structures, in addition to the multimaterial (rather than two-material) structures previously discussed, two additional important points should be considered.First, our model provides the time-dependent behavior of the curvature, which is a fundamental building block of shape shifting in multi-material structures. Other higher-level shape-morphing quantities, such as curling, twisting, coiling, and their combinations, originate from this quantity. Second, we discussed the time-dependent behavior of the curvature in one direction(narrow strip).For a plate having the same materials as those of the original narrow strip, the curvature would be the same in any direction(this point can be concluded by analyzing Ref. [47]), and can be modeled by the same two exponential terms of the original (parent)narrow strip developed in this article.For a plate that has different materials in different directions, the curvature would be different in each direction. However, the same two types of time constants and exponential terms proposed in this study can be used to model the time-dependent curvature in a specific direction accordingly. Future studies may incorporate the proposed two time constants (and exponential terms) in extensions to plates and so on.

It should also be noted that these concepts have been developed for multi-material structures that do not necessarily need to be multi-layer.In some cases(e.g.,graded multi-materials with gradients), the boundary between active and passive layers may not be as clear as those shown in Fig. 2. However, in these cases, eventually, the active and passive materials will have contact in some regions,and the same concepts developed in this study will be useful.In addition,multiple stimuli may also be used in some cases.In those applications,the fundamental individual concepts developed in this study can be useful as well.As one example,a recent study[96] found the Timoshenko bimetal model useful for modeling some parameters of electro-thermo-hygro reversible 4D materials.

Remark 6.Other manufacturing processes.We distilled three laws that govern the shape-morphing behaviors of nearly all the 4D multi-materials, whether fabricated by printing and so-called 4D-printed structures or produced by other manufacturing processes.

Stimuli-responsive multi-materials can be produced by various manufacturing processes. However, AM has some benefits. First,the same reasons that motivate us to use AM for conventional(passive) materials will motive us to utilize AM for stimuli-responsive(active) materials. In other words, 4D printing conserves the general advantages of AM (such as material waste reduction,elimination of molds,dies,and machining[97],and providing complex geometries) that are not present in other manufacturing processes. Second, printing helps us elaborate on the internal structures of multi-materials precisely to enable various shapemorphing behaviors.In other words,4D printing enables encoding local anisotropy[5]in multi-materials.In fact,before the introduction of 4D printing technology, researchers did not typically try to find a specific printing path by mathematics to yield a predictable and desired shape-morphing behavior after printing.4D printing is a new manufacturing paradigm that combines smart materials,mathematics, and AM, as illustrated in Fig. 13 [6].

Remark 7.SME.As explained previously,SME is not an intrinsic property [10]. The four shape-morphing mechanisms discussed,quantified,and unified in the second law can occur with or without an SME. These four shape-morphing mechanisms are the underlying physical concepts for the relative expansion and subsequent shape-morphing behavior in 4D structures.

Fig. 12. 4D structure with more than two types of materials.

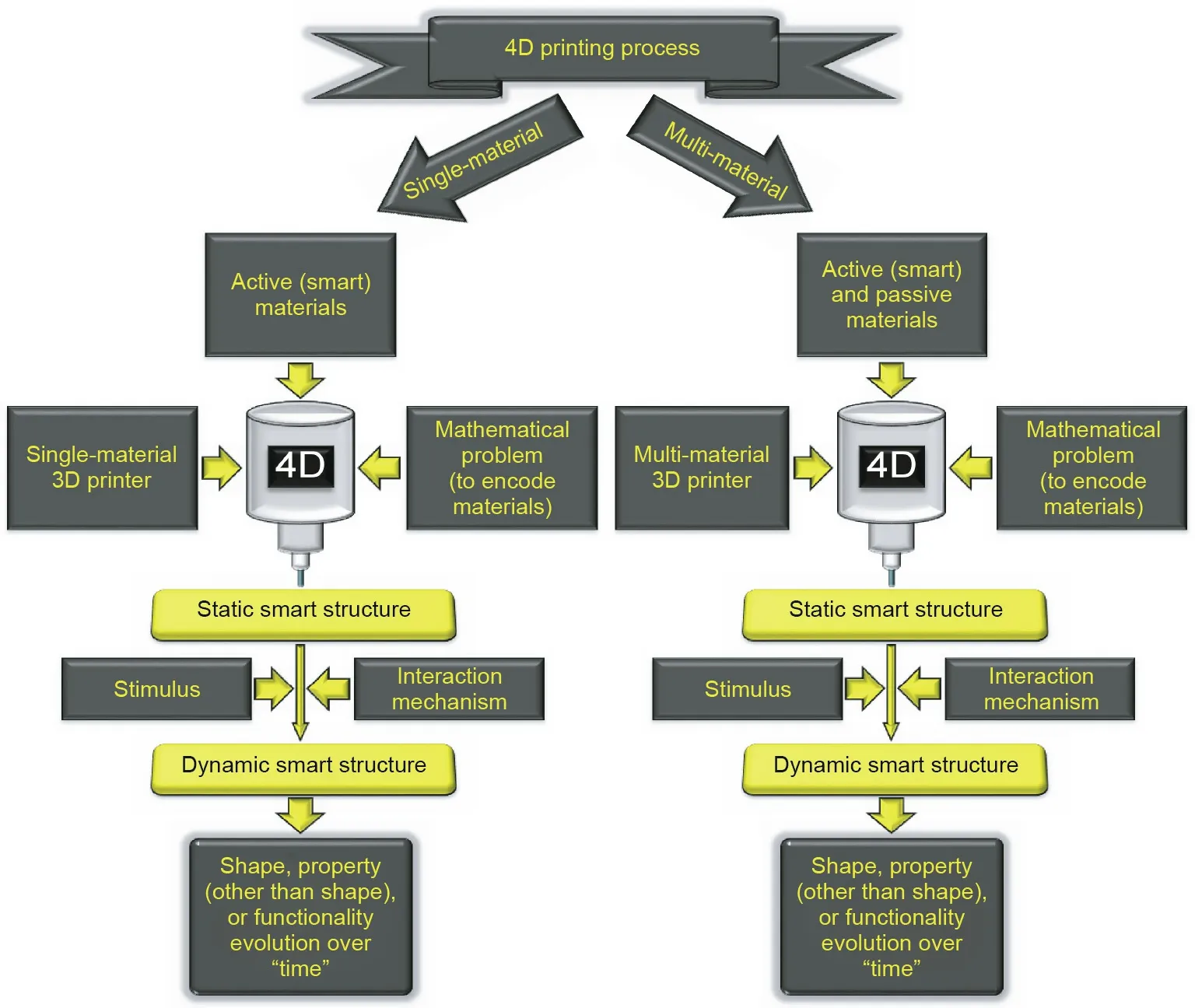
Fig. 13. 4D printing process [6]. Readers can also see the differences between 3D and 4D printing processes shown in Ref. [6].

For example, the ‘‘heat-responsive structure” shown in Fig. 5 illustrates a typical SMP (i.e., a polymer with an SME) in a bilayer with a passive material, and its shape-morphing behavior is enabled by the relative thermal expansion of the active and passive materials[36,37,91,98].The desired shape during the recovery step is induced by thermal expansion,and the SME determines(guides)the route of the shape change[98].In addition,the following analyses on the SME can be useful for both single- and multi-material structures.

Also useful is a discussion of the other modeling approach—the phase-transition modeling that is based on micromechanics modeling of the material (as mentioned by Diani et al. [102]).One of the main studies on this approach was conducted by Liu et al. [117] to model the evolution of microstructures in SMPs[76]. In addition, note that Hu et al. [76] considered the work of Liu et al. [117] as meso-scale modeling of SMPs. For small strains,Liu et al. [117] introduced an internal state variable called storage strain (stored strain) (εs), which is a ‘‘history” variable, to model phase changes. Some researchers analyzed the work of Liu et al.[117] and obtained an analytical equation for the storage strain.In their equation, the storage strain is directly proportional to stress (εs∝σ) [118,119]. Thus, according to their analytical model, if stress is zero in a process,εswould be expected also to be zero in that process. In addition, some other researchers such as Qi et al. [120] proposed a means of phase-transition modeling with no need to define a storage strain (stored strain).

Based on the aforementioned analyses,we did not consider SME as a specific category of fundamental physical concepts in the second law.

Remark 8.Applicability of the results of this study to singlematerial 4D structures. In the introduction, we discussed singlematerial versus multi-material structures in 4D printing and thus aimed at multi-material (active-passive) structures. However,our results can also be applied to single(active)materials.The first and second laws for single-material 4D structures would be similar to those for multi-materials because the shape-morphing behavior of nearly all smart materials is due to the expansion or contraction in the material.This expansion falls into one of the aforementioned four categories. This point is clear for most groups of smart materials and stimuli. Only for SMPs is further discussion needed. The key mechanism of the SME is the temperature-dependent mobility in SMPs [109]. In the previous remark concerning the SME, we clarified that the shape-morphing behavior of SMPs upon stimulus during recovery is (or can be) identified by the thermal strain εT,which is related to thermal expansion (one of the four categories of the second law).It should be remembered that the unified equations of the second law are all based on‘‘strain.”It might be interesting to note that when polymer chains are programmed mechanically, a molecular transformation (chain orientation in a specific direction) will occur as explained and quantified in the molecular transformation category of the second law. However,the most important part of the shape memory behavior is the recovery step [107], as the shape shifting is obtained through this step[12].The second law is mainly concerned with single-material 4D structures because the passive element in a multi-material 4D structure is not responsive (in general). Otherwise, it would be stimuli-responsive (active) rather than passive. Nevertheless, we used the word‘‘relative.”Finally,the third law is a transition from single (active) materials to multi (active-passive) materials. In addition, some of the results from and discussion about the third law can also be useful for single-material 4D structures. As one example, the general graph of Fig. 4 can also be used for singlematerial SMPs. A single-material SMP can have a curvature depending on the direction in which it has been programmed. It also does not possess the exponential term related to the mismatch effect between active and passive elements. For a monoexponential equation, the general trend of on and off regions would be similar to that of a bi-exponential equation. However,the slope of its graph at a similar point would be different from that of the bi-exponential model.

In addition to the previous note, from one perspective we can say that for single-material 4D structures,we mainly need the first and second laws,and for multi-material 4D structures,we need all the three laws.

Remark 9. Scope and exceptions. Throughout this work, we did not make any specific assumption regarding the types of materials,stimuli,and length scales(macro,meso,etc.)for which these three laws are valid.

However, two points should be made about the scope of this study.First, these three laws are about shape-morphing behaviors that are currently the focus of studies in the 4D printing field. In addition, as we mentioned in the introduction, following the TED conference [1], the first embodiment of 4D printing has been entitled‘‘4D printing:multi-material shape change”[2].Note the word‘‘shape” in the title of the work done by Tibbits [2]. This word has been used to introduce 4D printing. The evolutions of other properties such as color or thermal resistance have not been discussed in our study.Nevertheless,the shape-morphing behavior can alter other properties or functionalities in the desired manner.As an example, the researchers in Refs. [121,122] demonstrated smart patterned surfaces that can alter their geometries in a manner that leads to changes in their effective emissivity. This results in control of the satellite temperature without using conventional controllers and energy supplies. Second, in simple linear expansion/contraction shape-morphing behaviors, no curvature exists,where these behaviors may be considered as zero-curvature shape shifting for which the radius of curvature is infinity.

In science and engineering, laws are flexible and can have exceptions. We have reviewed a few hundred published works,including those on stimuli-responsive structures fabricated by printing or produced by other manufacturing processes. However,we could not find any exception (i.e., counter-example) to our laws.Nevertheless,we used the expression‘‘nearly all”in the three laws for possible exceptions in the future.As a side note,we should mention that our results are general and target the fourth dimension.

Some existing works at first glance may seem to present counter-examples to these three laws. However, based on an in-depth analysis and with their fundamental physics considered,their compliance with these three laws will be understood. For example, the built-in (direct) 4D printing proposed by some researchers [123,124] has the same ‘‘underlying physics” of conventional SMPs. As we noted earlier, to enable the SME of SMPs,a mechanical force is required in addition to heat (the thermomechanical(thermo+mechanics)cycles of SMPs indicate this point as well). In the built-in (direct) SME [123,124], this mechanical force(used for programming) is provided during the printing (i.e., the printing and programming steps are integrated).A similar concept was discussed in the introduction and has also been mentioned in other studies [34,37]. The underlying physics of the shapemorphing behavior of these examples is the same as the ‘‘heatresponsive structure” shown in Fig. 5 and discussed in Remark 7.

Sometimes, a formula is derived (and validated). However, it is valid and applicable only for a specific range of cases. The biexponential formula derived and validated in this article is a universal governing equation that can model and predict the fourth dimension of nearly any 4D structure. In our study,this generality was possible because we underpinned its bases comprehensively.We used the word ‘‘law” in this article because our results are general and are also required for understanding, modeling, and predicting the fourth dimension of 4D-printed structures.

Remark 10.Future works.By itself,3D printing is considered a multi-disciplinary field.Thus,more research areas will be involved in the 4D printing field. This diversity can increase the strength of 4D printing.

Future studies can consider several topics.One main topic is the compatibility of materials in multi-material structures. The materials should form a strong bond at their interface. Their bond should also remain strong under stimuli.Other topics include measurement and modeling of some of the parameters in the biexponential formula, such as time constants. Some parameters should be measured for active-passive materials, whereas models(whether case-specific or general)can be developed for other ones.Experimental studies can be conducted to find the exact values or the ranges of parameters for categories of materials. Other topics include software and hardware development and their integration.Future 4D printing software should have some levels of prediction.It can also provide the means of tuning the behavior over time.Future 4D printing hardware development requires some control strategies that can handle multi-material printing. Assume that ten materials are going to be encoded in a single-piece structure in various locations (voxels), with ten nozzles working simultaneously. Developing new smart materials with new applications is also a main research area. The printability of smart materials is the next topic. Many smart materials exist. However, they must become printable. Tuning the response speed is also a major topic. Still another topic is related to product development by 4D printing.4D printing is not just a concept;it is also a manufacturing paradigm. Therefore, new products or applications that can obtain unique features by 4D printing should be regularly considered.

Remark 11. Closing. Fig. 14 presents a summary of the proposed three laws.

3. Conclusions

We examined the fourth dimension of 4D structures and revealed three general laws that govern the time-dependent shape-morphing behaviors of nearly all 4D structures. The main purpose of the first and second laws was to understand the fourth dimension, and that of the second and third laws was to model (and predict) the fourth dimension. Through a detailed systematic qualitative and quantitative study, we derived and validated a universal bi-exponential formula that governs the fourth dimension. The results of this study can serve as general design principles for the future. They can also be incorporated into future software and hardware development in 4D printing.

It should be noted that a pure experimental study may not be able to generate a general conclusion concerning the relationship between two quantities, as it may not cover all possible regions of the relationship in various cases. Drawing a systematic conclusion is the strength of an analytical study(validated by experimental data) as conducted here.

Recently, many exciting demonstrations of 4D printing have been revealed that can hardly be achieved by other processes.However, more collaborations between scientists and engineers from various fields are needed to move from laboratory to fabrication and unveil the full potentials of 4D printing.

Historically,some topics are developed,enter research communities, and become popular; then, after a short period, they lose their broad interest. However, it is expected that 4D printing will remain attractive and useful for a long period because stimuliresponsive materials have already demonstrated their promising applications in various fields. 4D printing further helps us encode and elaborate on the structures of stimuli-responsive multimaterials by leveraging the strengths of AM (more specifically,printing) and mathematics, which are the other main elements of 4D printing.

Acknowledgements

Farhang Momeni wants to thank Shien-Ming Wu Manufacturing Research Center in the Department of Mechanical Engineering at the University of Michigan, Ann Arbor for support, and Andrea Poli for assistance in DMA tests in the Mechanical Testing Core directed by Ellen Arruda in the Department of Mechanical Engineering at the University of Michigan,Ann Arbor.For drawing the galactic shape of Fig. 14, we were inspired by a display designed by Rod Hill showing advancements in Reconfigurable Manufacturing Systems and installed on the wall of the Engineering Research Center (ERC) for Reconfigurable Machining Systems(RMS) at the University of Michigan, Ann Arbor. The authors hope that their results will be beneficial in ethical applications. Finally,the authors’ contributions are as follows: Farhang Momeni conceived the study, obtained and analyzed the results, and wrote the manuscript. Jun Ni discussed the results, reviewed the manuscript, and provided feedback.

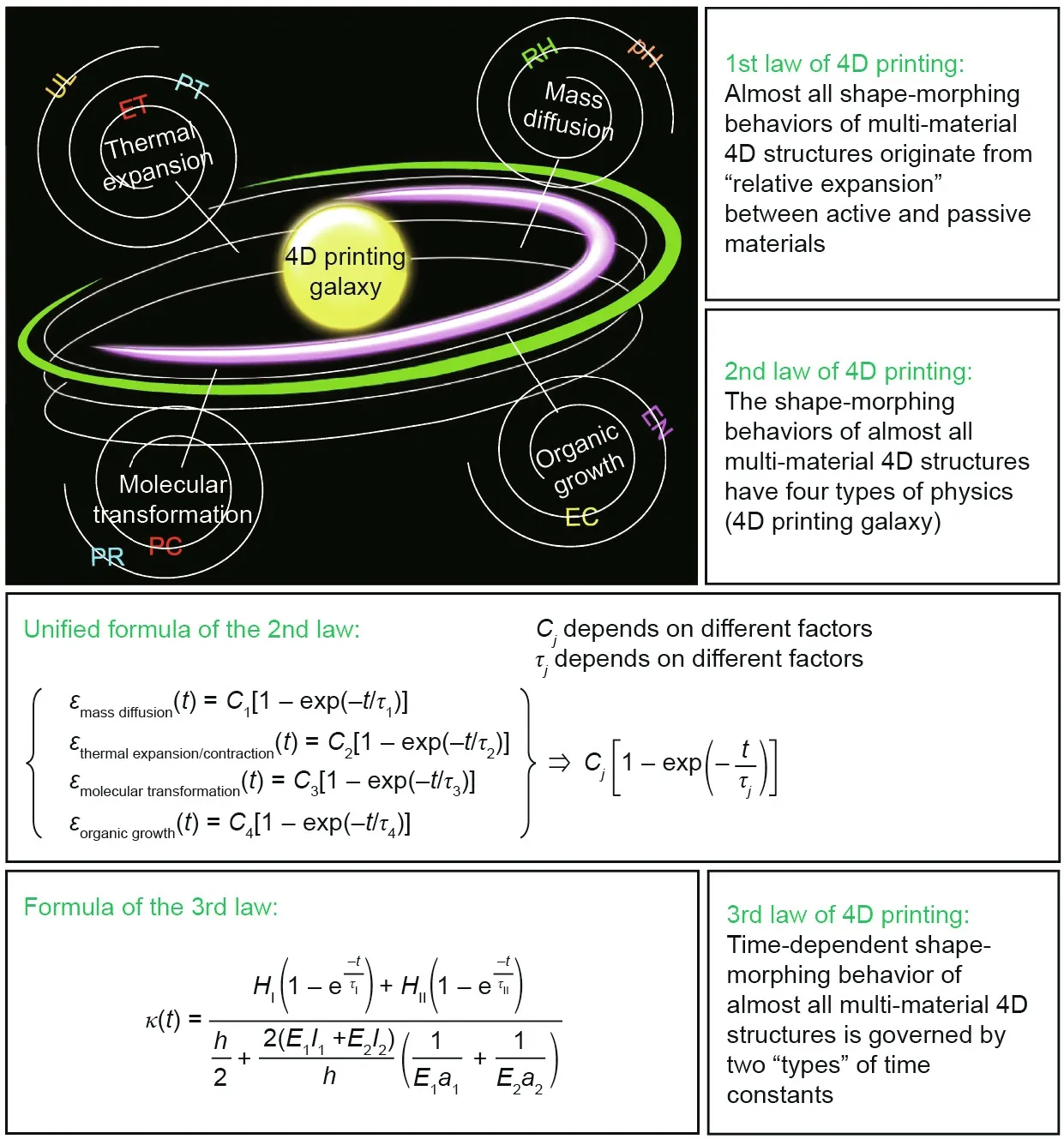
Fig. 14. Summary of the proposed 4D printing laws. RH, PT, ET, UL, PC, PR, EC, and EN denote relative humidity, photothermal, electrothermal, ultrasound, photochemical,pressure, electrochemical, and enzyme, respectively. Additional stimuli and mechanisms can be indicated in each of the four physical categories.

Compliance with ethics guidelines

Farhang Momeni and Jun Ni declare that they have no conflict of interest or financial conflicts to disclose.