基于层次分析-模糊理论桥梁网养护中的应用

唐 鹏,宫 赛

(1.长安大学 公路学院,陕西 西安 710064；2.南阳理工学院，河南 南阳 473004)

0 引言

随着公路网中桥梁数量的不断增多，桥梁在公路网中发挥着举足轻重的地位，在正常运营和自然环境作用下，在役桥梁的结构性能持续降低。因此有必要对在役桥梁的技术状况进行评定，目前国内外针对桥梁技术状况评定研究已取得显著成果，国内的评定标准主要有《公路桥梁养护规范》(JTG H11—2004)[1]、《桥梁技术状况评定标准》(JTG/T H21—2011)[2]等规范。国外以美国研究较早，主要有FHWA编写的《桥梁检测人员培训手册》、《国家桥梁结构报表于评价记录、编码指导》、AASHTO编写的《桥梁管养手册》等规范。

国内外学者[3-4]从路网的拓扑结构、行程时间、容量、畅通性、服务水平等不同角度对路网进行可靠性研究，公路网络系统性能的研究往往以道路为主体进行研究，桥梁管理系统中引入即构件层次(element-level)、项目层次(project-level)、路网层次(network-level)3个层次的可靠指标β。桥梁网络的性能应该从网络的连通性、使用者的满意度和关键桥梁的性能等3方面进行评定[5-6]，程寿山[7]、黄侨[8]提出基于模糊理论的桥梁评估理论研究及其应用，张俊光[9]等提出基于层次-模糊算法的独塔斜拉桥安全性评价，国内外研究学者往往以单座项目级桥梁作为研究对象进行分析，对有若干条桥梁组成的桥梁网进行评判研究及应用较少，目前仍处于探索研究阶段。现阶段桥梁技术状况评定的规范以层次分析法及赋予权重进行计算，此外对桥梁网的整体状况评判影响因素不一，存在不确定性和模糊性的特点。由此引入模糊理论，将模糊模式识别理论应用到桥路网的技术状况评判中。本文介绍利用层次分析法和模糊理论确定评估指标权重，提出：①桥梁网安全性的评估指标；②通过规范、专家评估和实际调查确定各指标层的权重；③通过模型计算分析得到桥梁网的评估结果。并以广东境内某高速路线上的桥梁网进行应用分析。

1 模糊理论和层次分析法的基本思想

1.1 基本思想

美国控制专家论专家Zadeh教授在1965年《Information and Control》的杂志上发表了一篇标志模糊数学诞生的文章《Fuzzy Sets》。模糊数学引进我国后，在工程实际应用等问题上得到了快速的的发展[10-11]。模糊理论引用到桥梁网评判主要包括以下几个主要步骤：

第一步，建立因素论域，将影响桥梁网整体的技术状况评定划分成n个因素，即U={u1,u2,u3,…,un,}。

第二步，建立评价等级论域，根据桥梁技术状况评定等级建立桥梁网整体技术状况等级，同样采用5类{1类、2类、3类、4类、5类}，即V={v1,v2,v3,v4,v5,}，分别代表安全状况优良、较好、一般、损坏、危险5个等级。

第三步，隶属函数的建立，对单因素的评价隶属度矩阵R在因素论域和等级论域基础上构造指标的评判矩阵R={r1,r2,r3,r4,r5,}，R为U到V上的一个模糊隶属关系矩阵，其中隶属度向量Ri={r1,r2,r3,…,rm}，建立模糊关系矩阵R:

第四步，层次分析法(Analytic Hierarchy Process)由20世纪70年代美国科学家教授Saaty提出简称AHP。层次分析法是把一个复杂的问题分解成多层次、多指标的递阶层次结构，在此基础之上进行定性和定量分析的决策方法,具有实用性、系统性、简洁性的优点。

我国《公路桥梁养护规范》(JTG H11—2004)[2]、《桥梁技术状况评定标准》(JTG/T H21—2011)[3]等规范对桥梁技术状况评定均是按照层次分析法进行计算评定，两种规范的区别主要是对桥梁结构构件的划分层次及权重划分不一。因此本文在评判桥梁网的总体技术状况时也基于这种方法，运用AHP方法解决具体步骤如下[12-13]：

a.明确和分析桥梁网系统中各基本要素之间的关系，建立桥路网评定的递阶层次结构。

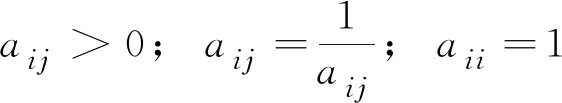
表1 1～9标度含义Table 1 1～9 scale meaningaij含义1ai与aj相比, 同样重要3ai与aj相比, 稍微重要5ai与aj相比, 明显重要7ai与aj相比, 强烈重要9ai与aj相比, 极端重要

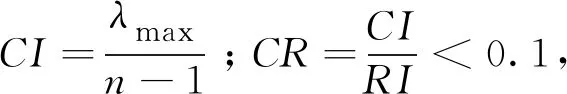
d.计算各指标的权重W={w1,w2,w3,…,wn}。主要利用层次分析法构造桥梁技网技术状况的层次模型，由加权计算方法从底层计算得到向上一层次状况，逐层计算，得到递阶结构每层指标相对于总目标的权重。

e.确定桥梁网整体技术状况等级。

B=(b1b2…bm)=W·R=(w1w2…wn)·

根据最大隶属度原则，设B1,B2…Bn为B的向量，B=max(B1,B2…Bn)。

1.2 建立桥路网评价模型

为了全面科学对桥梁网技术状况评定，采取JTG/T H21—2011规范已经评定完成的单座桥梁技术状况评定结果，以单座桥梁为基础引入桥梁技术状况、桥梁长度、桥梁美观、桥梁在路网中的地位等桥路网的评价指标建立模型，见图1。

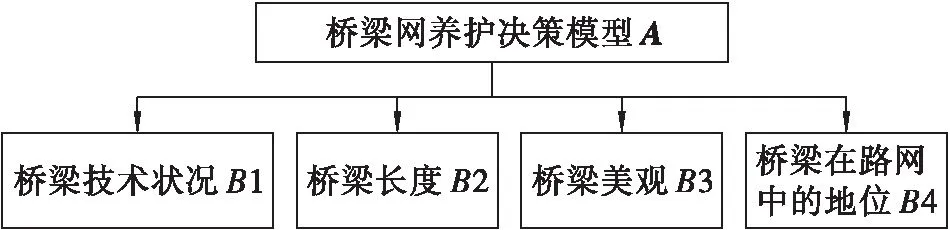
图1 桥梁养护模型Figure 1 Bridge maintenance model

3 案例分析

本项目为广州虎岗高速虎门港支线一期段(S304)：起于虎门镇博美村，沿轮渡公路走廊带延长线，跨虎门镇连升路、省道S256以及广深高速，设新联互通立交；经虎门镇及马城以南、远丰以北，于花灯盏水库北岸接入虎岗高速公路主线。路线全长约10.8 km(桩号位置K0+000～K10+779)。全线采用双向四车道高速公路标准，设计速度为120 km/h。本标段需要检查桥梁地理位置平面图及桥梁统计一览表，如图2、表1所示。检测共有桥梁23座，其中大桥17座，中桥1座，小桥5座，该段桥梁视为呈线性串联结构分布。

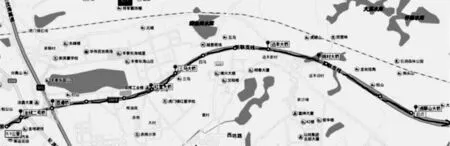
图2 桥梁地理位置平面图Figure 2 Bridge location plan

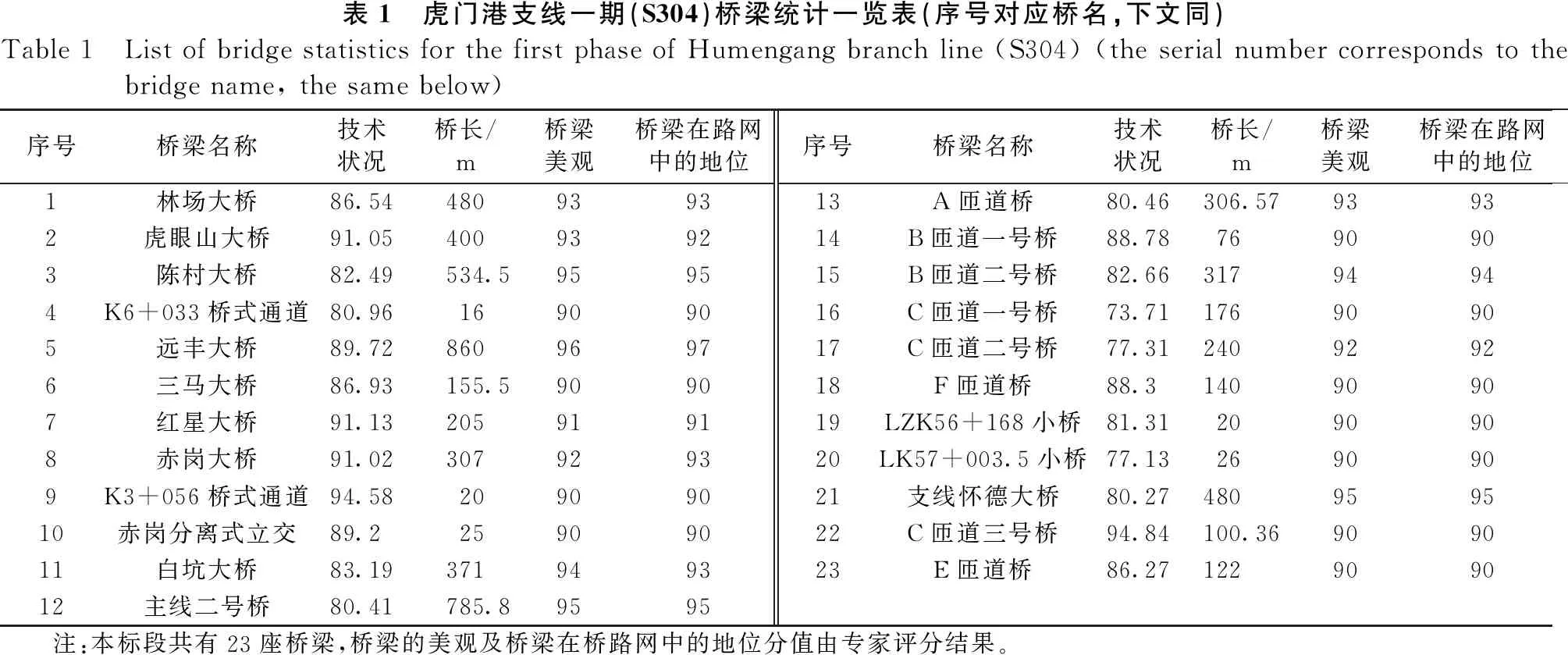
表1 虎门港支线一期(S304)桥梁统计一览表(序号对应桥名,下文同)Table 1 List of bridge statistics for the first phase of Humengang branch line (S304) (the serial number corresponds to the bridge name, the same below)序号桥梁名称技术状况桥长/m桥梁美观桥梁在路网中的地位序号桥梁名称技术状况桥长/m桥梁美观桥梁在路网中的地位1林场大桥86.54480939313A匝道桥80.46306.5793932虎眼山大桥91.05400939214B匝道一号桥88.787690903陈村大桥82.49534.5959515B匝道二号桥82.6631794944K6+033桥式通道80.9616909016C匝道一号桥73.7117690905远丰大桥89.72860969717C匝道二号桥77.3124092926三马大桥86.93155.5909018F匝道桥88.314090907红星大桥91.13205919119LZK56+168小桥81.312090908赤岗大桥91.02307929320LK57+003.5小桥77.132690909K3+056桥式通道94.5820909021支线怀德大桥80.27480959510赤岗分离式立交89.225909022C匝道三号桥94.84100.36909011白坑大桥83.19371949323E匝道桥86.27122909012主线二号桥80.41785.89595注:本标段共有23座桥梁,桥梁的美观及桥梁在桥路网中的地位分值由专家评分结果。

4 应用分析

4.1 项目级桥梁养护迷糊综合评价

首先计算单座项目级桥梁的构件和部件的得分，得到上部结构、下部结构、桥面系的得分，根据部位的权重，以此得出单座桥梁的技术状况评分。图3分别显示本次检测巡检23座桥梁上部结构、下部结构、桥面系技术状况评定情况。

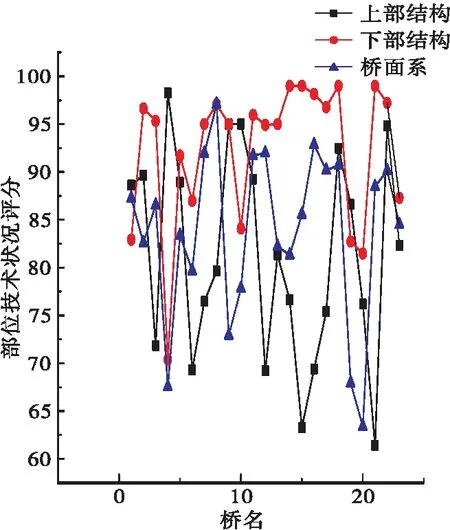
(a)部位评分

(b)总体评分

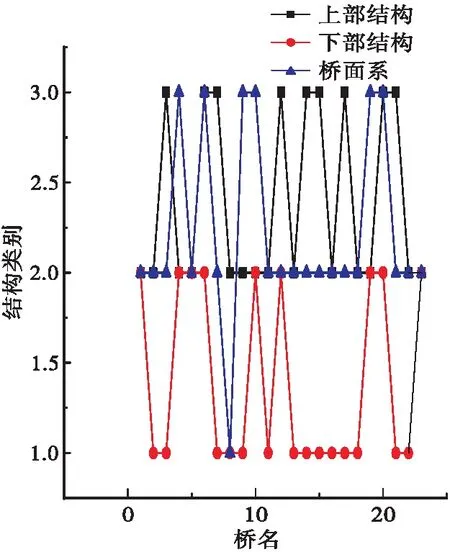
(c)评分类别

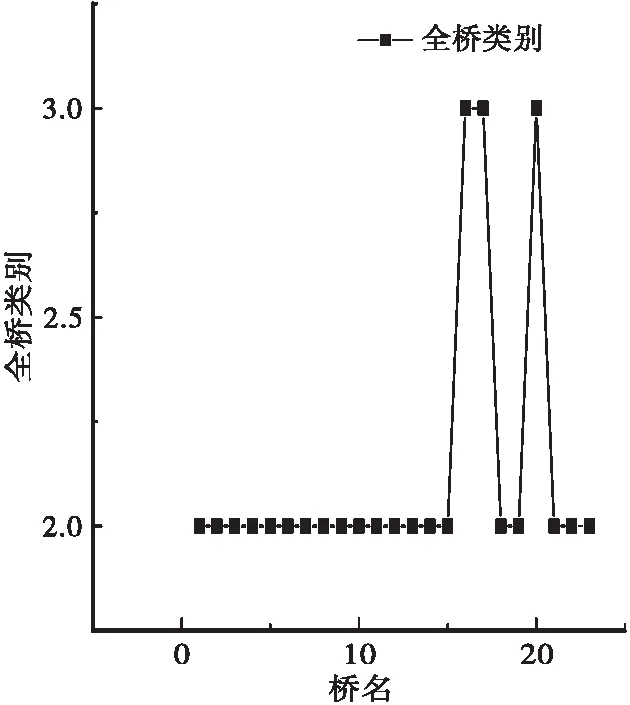
(d)评分类别 (e)按桥型桥梁总体技术状况等级 (f)桥梁部位技术状况等级评定结果统计表

根据对本次检测评定结果的分类汇总分析，图4通过计算得到23座桥梁在技术状况评定标准下桥梁的技术状况评定等级所占比。

图3中(b)、(c)分别显示本次检测巡检23座桥梁上部结构、下部结构、桥面系对比和网级桥梁总体的技术状况等级情况情况，同样的，显示下部结构等级较高，大多划分为一类和二类，图3(d)显示本次检查共共发现有桥梁3座评定为3类，图3(e)显示大、中、小桥在整个桥梁网中的技术评定等级，图3(f)显示下部结构评定等级高的数量较多，上部结构和桥面系数量大体相当。图4中显示该路网中的桥梁上部结构、下部结构、桥面系技术状况等级较高。

4.2 路网级桥梁养护迷糊综合评价

通过对专家调查的汇总和评分，桥梁网桥梁技术状况、桥梁长度、桥梁美观、桥梁在路网中的地位指标的相对重要性进行两两比较，见表2。

λmax=4.015 2,代入一致性检验式CI=0.05<0.1，该矩阵满足一致性检验。

(i=1,2,3,4;j=1,2…23)

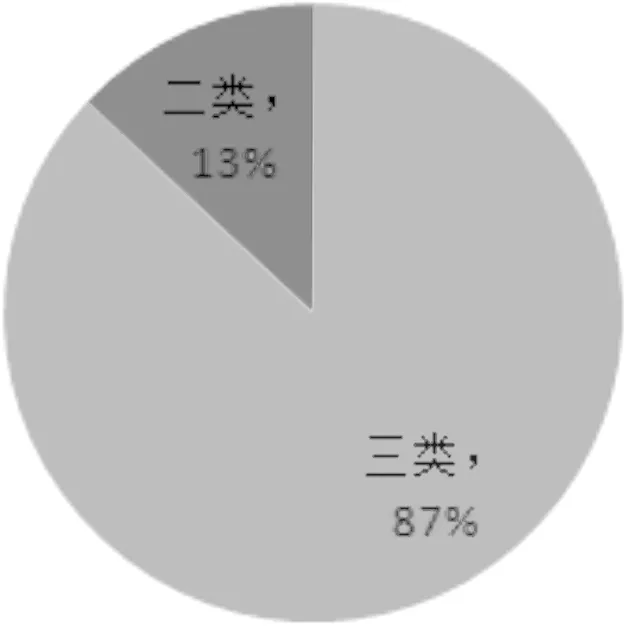
(a) 路网级桥梁总体技术状况等级占比图

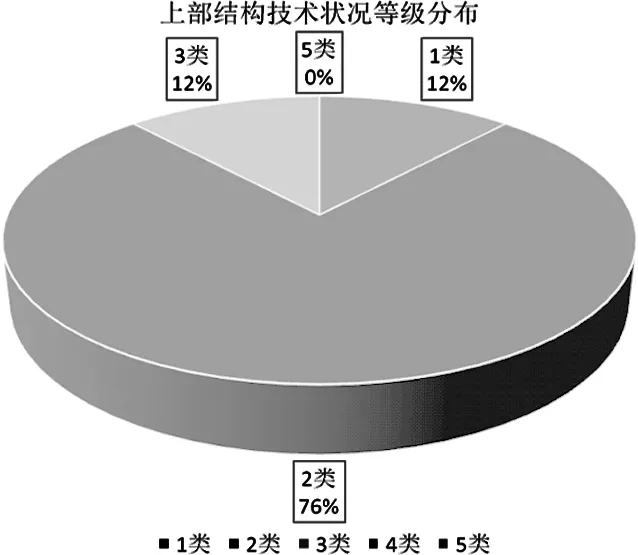
(b) 路网级桥梁上部结构技术状况等级占比图

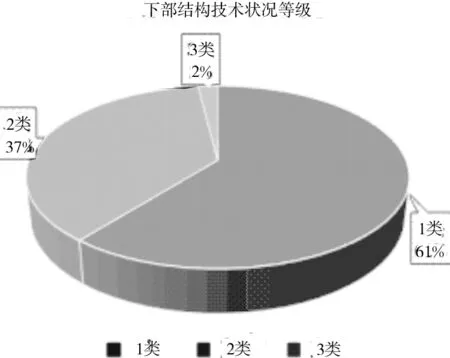
(c) 路网级桥梁下部结构技术状况等级占比图

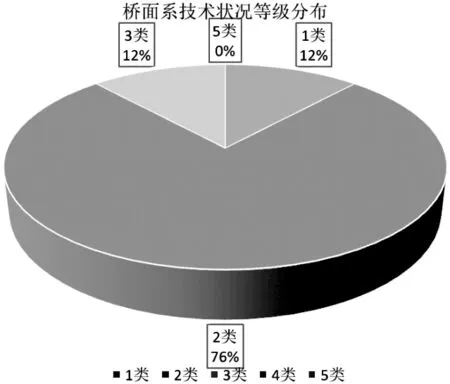
(d) 路网级桥梁桥面系技术状况等级占比图

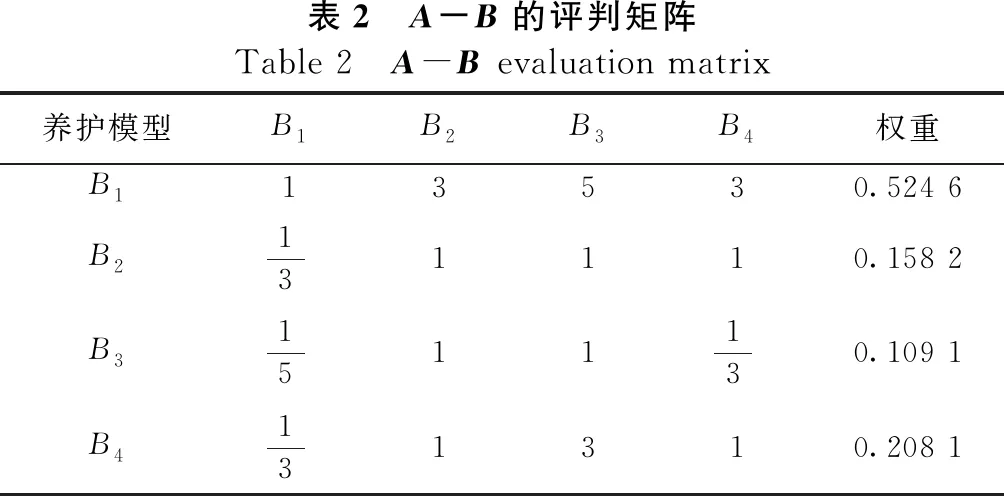
表2 A-B的评判矩阵Table 2 A-B evaluation matrix养护模型B1B2B3B4权重B113530.524 6B2131110.158 2B31511130.109 1B4131310.208 1

桥梁网桥梁技术状况、桥梁长度、桥梁美观、桥梁在路网中的地位各因素的权重如下：

A=(0.524 6,0.158 2,0.109 1,0.208 1)。

B=A*R=(0.049 1,0.048 3,0.050 2,0.035 7,0.060 5,0.040 9,0.043 3,0.045 9,0.039 5,0.038 2,0.045 4,0.056 1,0.043 5,0.039 4,0.043 9,0.037 9,0.040 8,0.040 9,0.035 9,0.035 0,0.048 1,0.041 6,0.039 9)。

通过路网级桥梁的层次-模糊理论综合计算，这23座桥梁的综合技术状况优良顺序依次为：20,19,21,2,23,11,13,17,7,5,16,22,14,6,15,4,9,10,3,1,18,12,8。

5 结论

a.基于层次分析法-模糊理论建立桥梁网的结构层次及指标体系模型，研究提出桥路网的安全评价方法。

b.结合国内外研究,提出路网级桥梁技术状况等级判断方法中引入桥梁网桥梁技术状况、桥梁长度、桥梁美观、桥梁在路网中的地位的4个指标。

c.以广东境内某条高速公路为工程背景，将研究提出的方法进行模糊评价，按照提出的计算模型进行模糊计算，得出该路段基于项目级及路网级桥梁的优良顺序。

d.该桥路网评价模型的建立为今后路网桥梁养护建设和资金优化的评价奠定了有效基础。