基于前馈复合控制策略的低频纹波抑制

周 浩，廖冬初，蔡华锋，范文超，张 鑫

（湖北工业大学，湖北 武汉 430070）

0 引 言

能馈型直流电子负载是一种由电力电子器件构成的可以实现负载模拟功能的电力电子装置，主要采用两级式单相并网逆变拓扑[1-3]。其中，前级DC/DC负责模拟负载、并网输入电压匹配以及电气隔离，后级逆变器负责将前级的能量回馈至电网。由于逆变器输出瞬时功率以两倍的工频脉动，该低频纹波会反馈至输入端，导致直流变换器的输入和输出电流中包含大量低频纹波[4,5]。对于前级DC/DC变换器而言，当电流平均值一定时，二次纹波电流会导致电流有效值增大，导致开关管的电流应力和通态损耗增大。前级DC/DC变换器采用软开关技术，二次纹波电流会减小软开关的作用范围，增加开关损耗，降低变换器的效率[6]。

有学者提出，通过增大母线电容容量，减小母线电容在两倍工频处的容抗，能够抑制纹波电流。但是，较大的母线电容降低了变换器的动态性能，增大了系统体积和重量，同时提升了价格。增加一级功率解耦变换器可以减小母线电容，但变换器需要添加额外的开关器件和控制电路，增加了系统控制的复杂性，降低了运行的可靠性[7,8]。

文献[9]提出，在前级DC/DC变换器采用电压电流双闭环控制的基础上引入含有两倍输出电压频率陷波器的负载电流前馈，以抑制母线电感电流纹波，但并未考虑此时输入电流的波动大小。文献[10]通过前级DC/DC输入电流PID单环控制降低了DC/DC输入端的低频纹波，但是母线电感电流的纹波依然可以达到30%波动，且传统PID具有延时性，无法及时跟踪给定信号，导致系统的动态特性较差。

本文提出一种复合控制策略抑制输入和输出低频纹波。通过建立变换器的欧拉-拉格朗日数学模型得到无源控制规律，在此基础上引入母线电感电流前馈。实验和仿真验证表明，该控制策略具有可行性和有效性。

1 低频纹波产生原理

如图1所示，本文中能馈型直流电子负载前级采用ZVS移相全桥，后级是并网逆变。假设电网的电压为理想的正弦波，则电网电压可表示为：

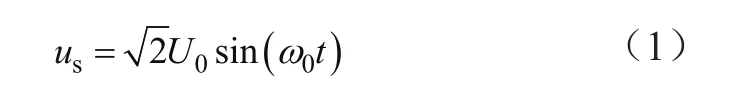
式中，ω0=2πf0，f0=50 Hz；U0为电网电压的有效值。逆变器的输出电流为：

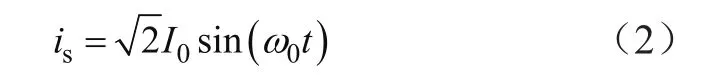
式中，I0为并网电流的有效值。

由式（1）和式（2）推导出逆变器输出瞬时功率p0为：

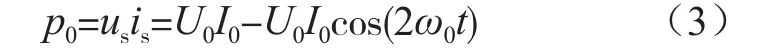
式中，瞬时功率包含两部分，一部分为恒定直流量的功率U0I0，另一部分为U0I0cos(2ω0t)即两倍的基波频率脉动。根据功率守恒，逆变器输入侧包含两倍输出电压频率的脉动电流。此时逆变器输入电流表示为：

式中，Idc为逆变器输入电流直流分量；i2nd为逆变器输入电流二次纹波分量，由前级DC/DC输出电感Lf和母线电容Cdc提供。当二次纹波电流经过中间母线电容时，以Buck电路为基础进行分析：

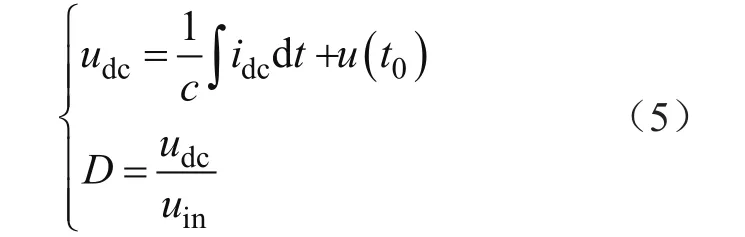
式中，D为变换器的占空比；udc为直流母线电压；uin为直流输入电压。式（5）表明二次纹波电流引起的占空比中存在二次纹波分量，当由前级输出电感Lf提供二次纹波电流时，则二次纹波分量会传递到前级DC/DC的输入电流。

变换器的输入电流表达式为：

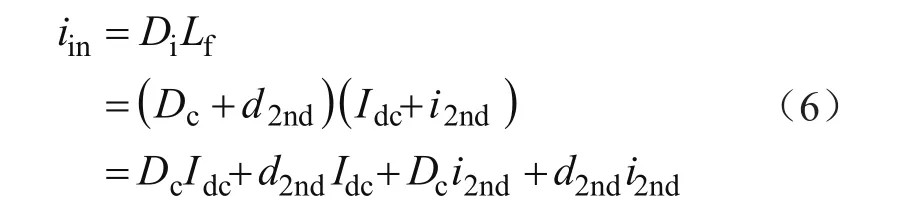
式中，Dc为占空比直流分量；d2nd为占空比交流分量；Idc为母线电感电流直流分量；i2nd为母线电感电流交流分量。式（6）中输入电流包含二次纹波分量，但是 |d2nd|＜＜|Dc|、|i2nd|＜＜|Idc|，因此二阶交流项d2ndi2nd将远小于一阶交流项Dci2nd+d2ndIdc，可忽略二阶交流项。输入电流的二次纹波主要是由于占空比和前级DC/DC输出电感电流波动引起的。

2 变换器E-L数学模型推导

电路拓扑如图1所示，其中iin为输入电感电流，i1为DC/DC桥臂电流，Lin输入滤波电 感，Cin为输入滤波电容，ucin为输入电容电压[11,12]。

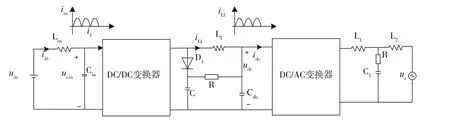
图1 主电路拓扑

当DC/DC开关管开通时，i1≠0，有：

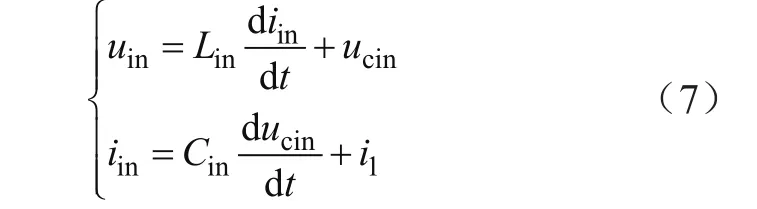
当DC/DC开关管关断时，i1=0，有：

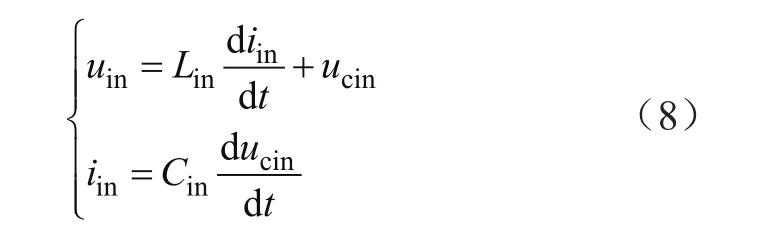
联立式（7）和式（8）可得，平均状态方程为：

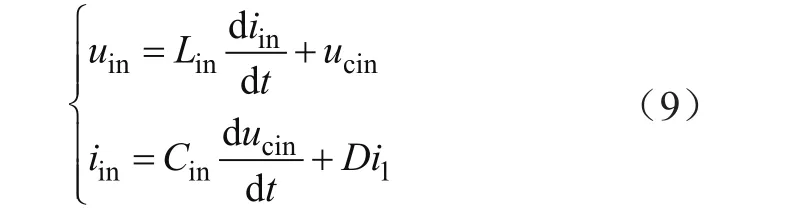
将式（9）转化为欧拉-拉格朗日方程形式为：

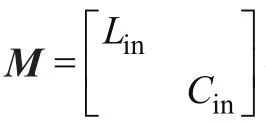
3 复合控制器的设计与仿真

3.1 复合控制的设计

由变换器的平均状态方程（9）可得：

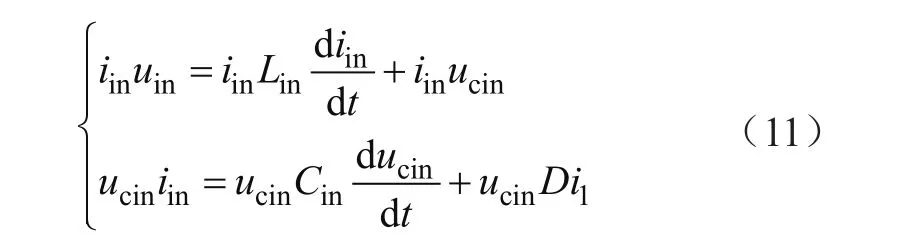
将式（11）中两方程相加，得：

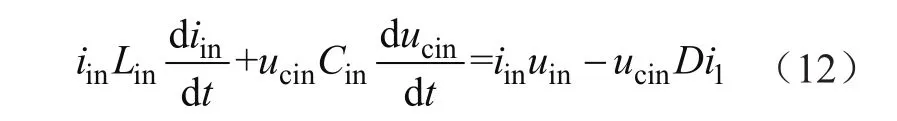
对式（12）两边同时积分，得：

由式（13）和式（14）可知，系统是耗散且无源的。当系统工作在稳定状态时，期望输入电容电压Ucin和输入电流iin仅存在较小的纹波，因此选取期望稳定平衡点iin=ir、ucin=ur。设系统的状态误差向量为xe=xxr，由式（10）可得误差动态方程：

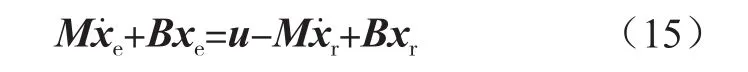
设系统存在的误差存储函数为：

从式（19）中发现，HE→0的速度取决于Ra，提高Ra能够改善控制器的性能。

在实现ZVS移相全桥过程中，由于副边的整流桥存在同时导通的情况，会造成副边占空比丢失，导致原副边占空比不相等的现象。两边占空比满足：

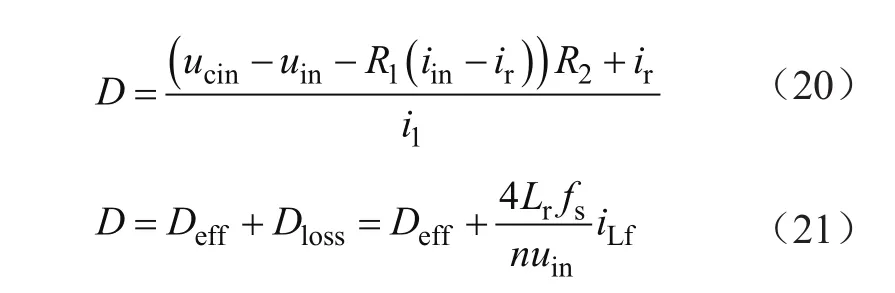
由式（6）和式（20）可知，输出电感电流与输入电流、占空比有关，说明占空比的波动导致了输入和输出电流波动[13,14]。而占空比的波动又是由母线电感电流中的低频波动引起的，因此加入母线电感电流前馈抑制输入电流和母线电感电流的波动，则可以得到新的控制规律：

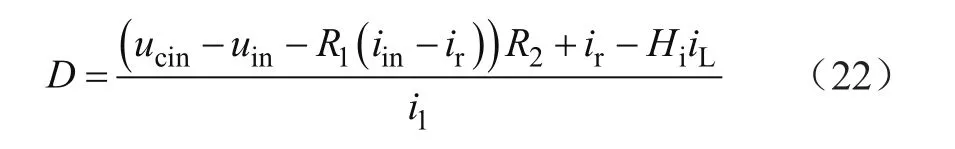
式中，Hi为调节系数。

将式（21）代入方程（9），得：

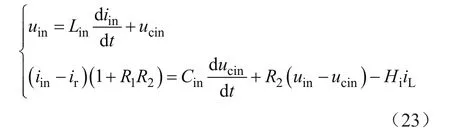
由式（23）可知，为方便调节，应调整R1→0(R1＞0)，然后R2和Hi协同调节。由前面的分析可知，输入电感电流和输入电容电压中均存在二次纹波，因此合适的Hi可以抵消纹波分量。

3.2 复合控制器的仿真验证

为证明上述控制，通过MATLAB/Simulink搭建70 kW直流电子负载的仿真模型，主电路参数如表1和表2所示。前级DC/DC采用的控制策略如图2所示，后级逆变器为母线电压外环并网电流内环控制策略。为抑制整流桥中二极管结电容和变压器漏感形成的谐振尖峰，在整流桥后接RCD电路，当出现尖峰时，二极管钳位，电容存储能量。尖峰消失后，电容通过电阻向母线电容释放能量，仿真参数R1=0.8，R2=20。

表1 电路参数

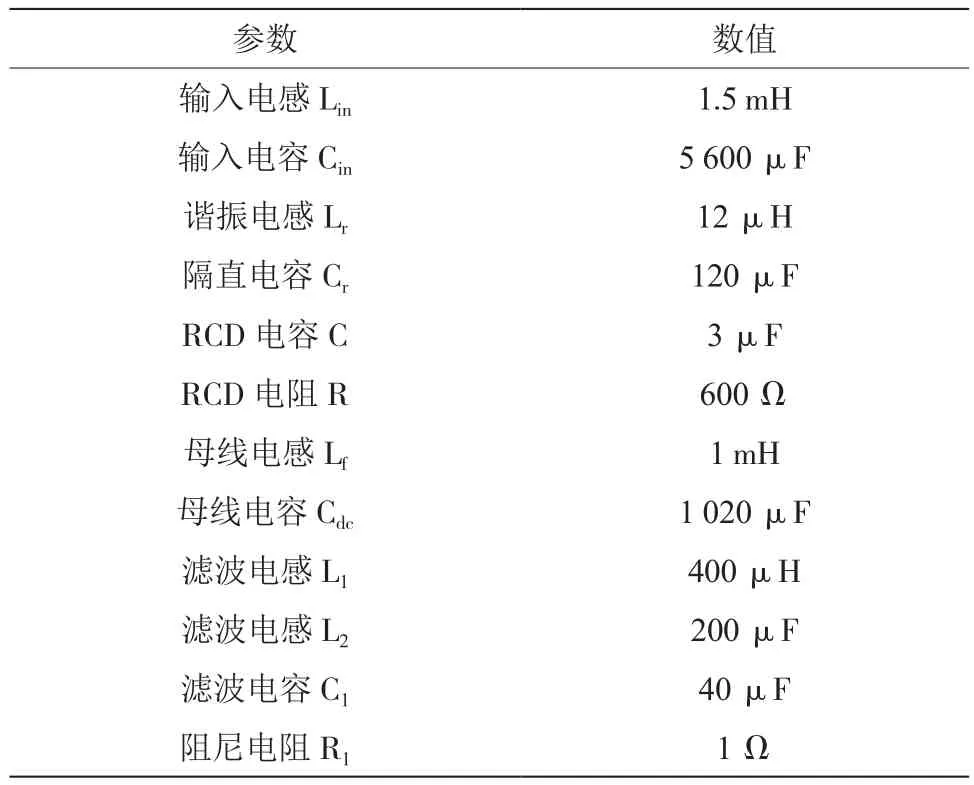
表2 元件参数

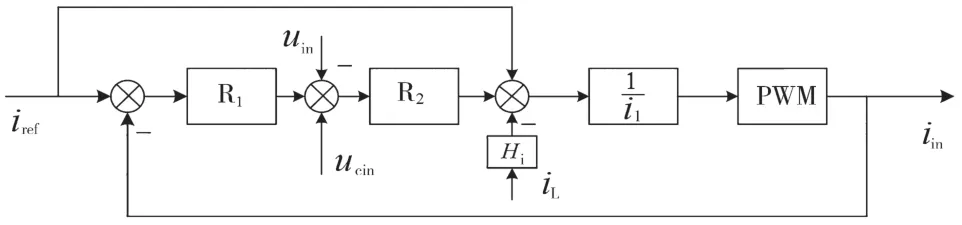
图2 复合控制下DC/DC控制框图

仿真结果如图3～图6所示，其中系统的软起动时间为0.15 s。图3为前级DC/DC采用PID电流单环控制策略，在0.05 s内输入电流没有及时跟踪给定值，当系统达到稳态后，输入电流纹波大小为2%。改为复合控制时，软起动得到了明显改善。当到达稳态值后，输入电流几乎没有波动，近似为一条水平线，同时无超调出现，即复合控制有效抑制了输入电流中的二次纹波。图5和图6是母线电感电流的波形。通过比较可以发现，复合控制在有效抑制输入电流中的低频纹波时，同时将输出电感电流的纹波从20%降低至10%。

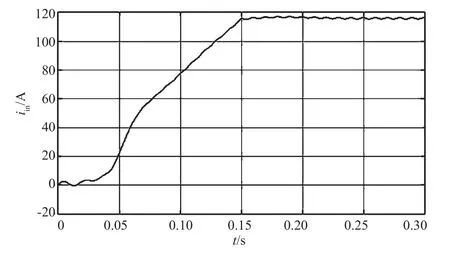
图3 PID控制下DC/DC输入电流

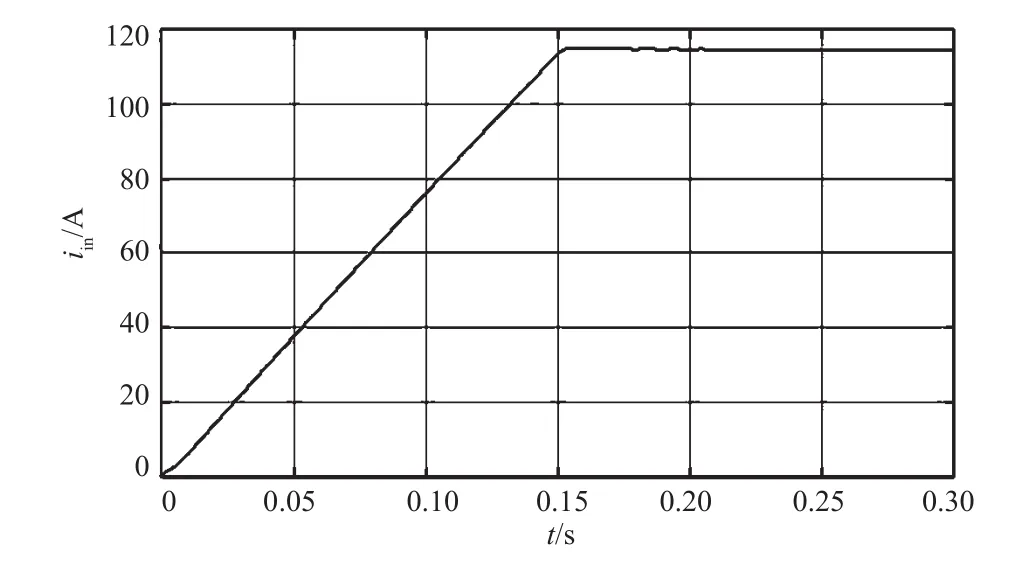
图4 前级复合控制下DC/DC输入电流

实际工程中有时会出现负载突增或突减情况，为了解系统此时的动态响应速度，通过仿真来模拟该过程。如图7所示，当输入电流完成软起动后，稳定运行1 s，给定电流值突减40 A，持续运行1 s后再突增40 A。可以发现，当情况恶劣时，输入电流快速跟踪给定值，以到达稳态值，说明系统具有较好的动态响应速度。

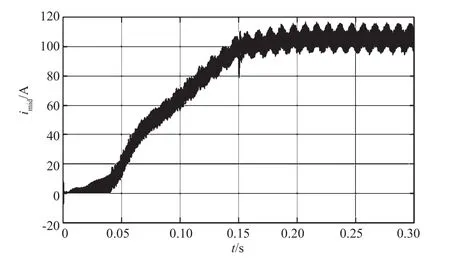
图5 前级PID控制下母线电感电流

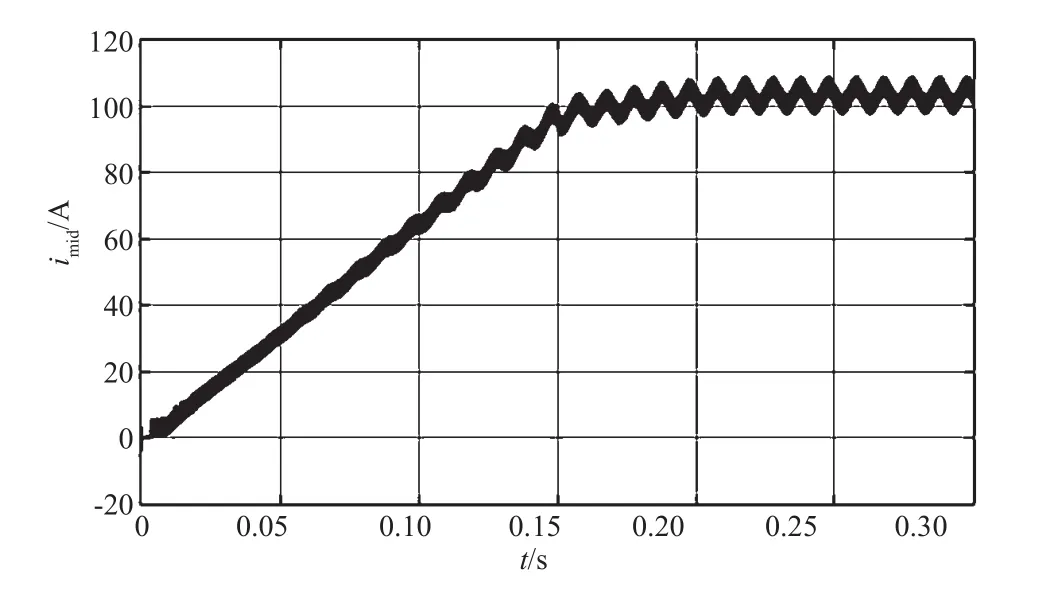
图6 前级复合控制下母线电感电流

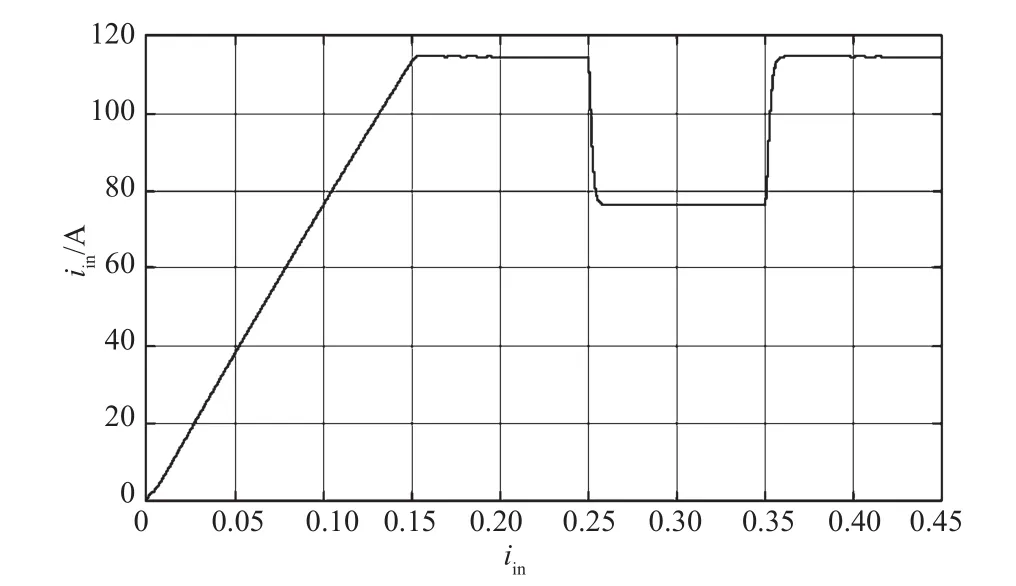
图7 前级输入电流突增和突减

4 结 论

本文分析能馈型电子负载中两倍频纹波的来源和传输方向，指出前级DC/DC电流单PID环控制的不足，建立欧拉-拉格朗日数学模型得到无源控制规律，使输入电流能够及时跟踪给定值，改善了电流的稳态值，进而提出一种母线电感电流的前馈复合控制改善占空比，在保持输入电流较低情况下，能够间接减小母线电感电流纹波至10%左右。最后，通过大量的仿真验证控制策略的合理性，有效解决了当功率增大时如何保证能馈型直流电子负载稳定运行。