多级陡坡消力池内流场的数值模拟研究

尹舒倩

（新疆维吾尔自治区水利水电勘测设计研究院，新疆乌鲁木齐830000）

1 概述

某水电站的设计装机容量80 MW，发电引水设计流量为110.8 m3/s。设计工况下多年平均发电量2.191 亿kW·h，保证出力5.3 MW。该电站在泄水闸后布置了多级泄水陡坡，多级陡坡长度为484.64 m，由进水口段、多级陡坡消力池段、尾水引渠段构成，该电站尾水引渠段采用梯形断面，其余部位均采用矩形槽断面型式。

多级陡坡的消力池陡槽段总长度为335.230 m，设计结构为现浇钢筋混凝土结构型式，纵坡1/3.82，由于水流流速较大，陡槽设置两级消力池。一级消力池底宽为4.0 m，纵坡为1/3.295，池长20 m，坎高2 m，底宽4 m。二级消力池，消力池池前底宽由4.0 m 渐变至8.0 m，长30 m，高差7.853 m；消力池长度为45 m，消力池深度为3.5 m，边墙高度为8.5 m。三级消力池底宽为4 m，池深11.5 m，消力池长度为35 m，消力坎高度为3 m。尾部渠道纵坡为i=1/264.188，长度为256.262 m，首部渐变段长30 m，宽度由8 m 矩形槽渐变为2.5 m 梯形渠道，边坡1∶2。

此次以该水电站梯级开发中的第3 级引水式电站泄水陡坡内部流场为研究对象，为探究陡坡及消力池内部水流运动状态，采用数值模拟的研究方法，运用目前求解水气两相流较为常见且模拟较准确的方法[1，2]，即采用双方程模型计算模型[3，4]，结合VOF 方法求解离散方程，对多级陡坡消力池进行三维水气两相流数值模拟。通过计算成果分析，可得到水流经过三级陡坡及消力池后，水流流速的降低幅度，得出该消力池效能效果。研究成果可为优化消力池提醒提供理论依据。

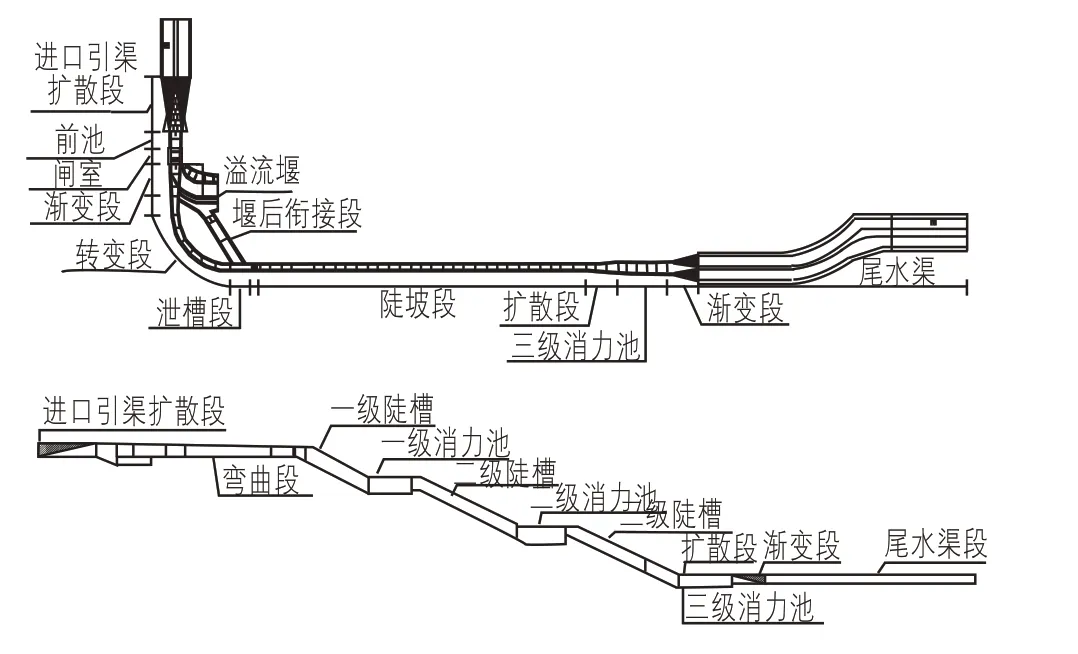
图1 模型布置图

2 模型及边界条件

2.1 模型及工作原理

电站泄水陡坡模型布置如图1 所示，为模拟研究多级陡坡消力池内部水流运动状态及消能效果，将试验模型进行简化，突出模拟研究对象，在数值模拟计算过程中，仅建立多级陡坡段及渐变段模型进行探究。根据消力池构成特点，建立一级陡槽、一级消力池、二级陡槽、二级消力池、三级陡槽、扩散段、三级消力池、渐变段模型。为探究泄水陡坡布置和水力设计的可行性，提出优化泄水陡坡设计的技术参数，此次试验模拟过程采用校核水位对设计方案进行校核。

2.2 数学模型

基于紊动能计算模型方程k 的基础上，结合紊动耗散率方程ε 方程，形成了双方程模型k-ε 计算模型。双方程k-ε 模型是由Launder 和Spalding 于1972年提出的。计算模型中的ε 定义如下：

于是，紊动粘度μt可表示成k 与ε 的函数：

因此标准k-ε 的输运方程为：

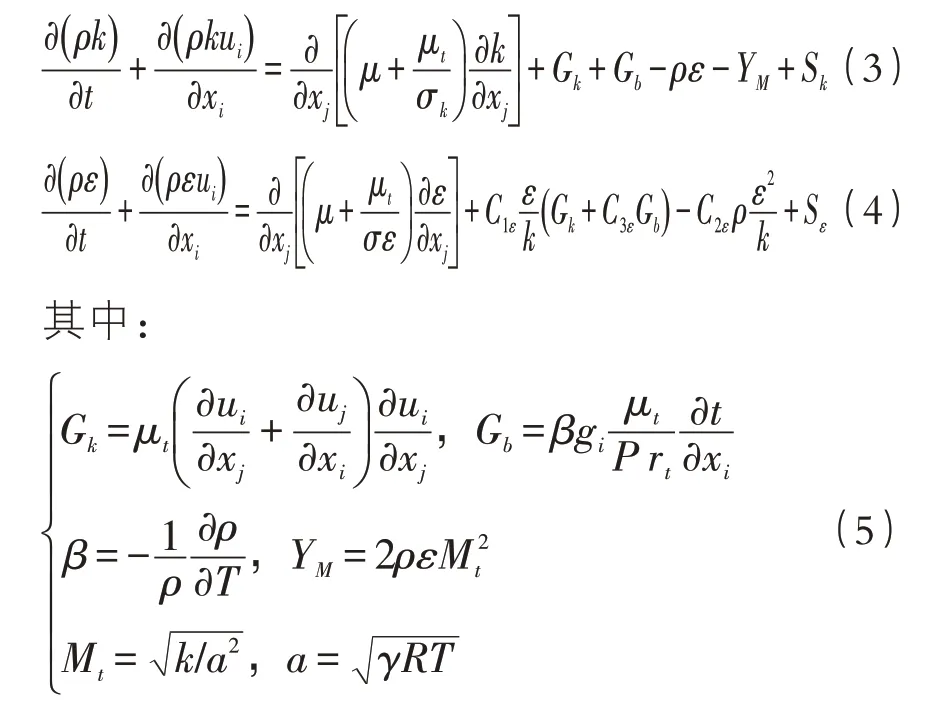
式中：Gb是由于浮力影响引起的紊动能产生；Gk是由于平均速度梯度引起的紊动能产生；YM为可压缩紊流脉动膨胀对总的耗散率的影响；C1ε，C2ε，C3ε为经验常数，通常分别为1.44，1.92，0.09；σkσε为普朗特数，分别与紊动能和紊动耗散率对应，一般为σk=1.0,σε=1.3；P rt表示紊动普朗特数，取0.85；gi为重力加速在i 方向上的分量；β 表示热膨胀系数；Mt表示紊动马赫数；a 表示声速。

采用欠松驰迭代方法对离散方程组进行求解，采用VOF（Volume of Fluid）模型[5]模拟三维水气两相流的自由表面。与VOF计算模型结合后，ρ 和μ不是一个常数，而是体积分数的函数，其方程即：

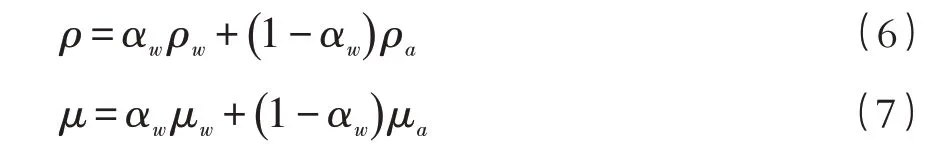
式中：ρw和ρa分别为水和气的密度；μw和μa分别为水和气的分子黏性系数。

2.3 网格划分

模型计算网格类型采用结构化网格与非结构化结合的方式[1]。非结构化网格具有计算速度宽，网格划分构成难度大的特点；非结构化网格的特点是构成简单，但计算稳定性较差。在保证节相同点间距前提条件下，结构化网格远小于非结构化网格数量，计算耗时相对较长，为此模型网格划分过程中，以结构化网格为主。由于模型结构规则，划分结构化网格易于实现，因此采用结构化网格；但消力池内部水流为紊流，为精确模拟消力池内部水流运动状态，在消力池附近网格划分较密。优化后网格总数为78 474 个。

2.4 边界条件

多级陡坡消力池计算模型内部包含水和空气两种介质。计算模型内部将水定义为主相，空气定义为次相；将水的密度定义为1 000 kg/m3。水流进口定义按照设计水位和校核水位设定静水压力边界；将进水口水流上部、模型顶部与模型出口水流上部空气接触面定义为压力进口边界，设置气压力进口边界的压强设置为0。为保证水流能够自由出流，得出泄水陡坡泄槽内水流及消力池内部水流的真实运动状态，将水流出口边界定义为压力出口。所有溢洪道的固壁边界均定义为无滑移边界条件，对粘性底层采用壁函数来处理。

泄水陡坡的初始条件：设定模型内部初始流场充满空气，运用瞬态时间相关模拟，模拟计算水流由外面随时间推移流入模型内部，继而通过对迭代求解体积分数，自动模拟模型内部的水气交界面，即为自由水面，水流将逐步充满整个流场，达到稳定的流态。

3 计算结果及分析

为探究泄水陡坡泄槽段及消力池内部水流，运用标准k-ε 计算模型结合VOF 计算模型进行求解。根据大量研究成果[6-8]，三维水气两相流流场的数值模拟中，采用此计算模型模拟计算的流场较为真实[9，10]，本文即采用前期研究成果直接进行模拟计算。经迭代计算，达到进出口参数平衡后，提取泄水陡坡泄槽段、消力池段的模型计算结果。对泄槽段、消力池段水气两相流流场及流速矢量场进行提取分析，所得成果如下。

3.1 流畅分析

通过数值模拟分析，模拟泄水陡坡内部水流运动状态，得到校核工况下泄水陡坡内的水气两相流分布云图。从云图观察可知，泄水陡坡泄槽段水面线连续光滑，水面沿程下降，即表明泄槽内水流流速逐渐增大；经观察发现，在各级陡槽下游反弧段受其体型影响，水面有微小起伏，由此表明该处水流发生小突变。

通过观察消力池内部水流可见，消力池内部水流波动起伏较大，水跃发生在各级消力池的前端，即表明消力池内部消能较充分；通过三级消力池内部流场对比，可发现相较于前两级消力池，第三级消力池水跃漩滚剧烈，水面波动起伏较大，部分水面接近边墙高。由此可见，第三级消力池尺寸需进一步优化，可将消力池边墙加高，或将消力池池长加大。

3.2 流速场分析

校核工况下各级泄水陡坡及消力池内水流运动状态见图2。由图2（a）（c）（e）可看出水流流经各级泄水陡坡时，内部流场平顺，泄水陡坡内部水深较小，流速较大；由于第一、二级陡坡的比降为1∶3、第三级陡坡的比降为1.00∶2.84，因此各级陡坡内流速随流程的增加而增加，数值模拟得出结论与实际相符。提取数值模拟计算所得流速数据见表1，由表格数据观察看出，水流流经泄水陡坡流速逐步增大，流至各级消力池内，水面波动剧烈。通过图2（b）可看出第一级消力池水跃发生于泄水陡坡末端，未进入消力池池内，且水流波动结束于第一级消力池中后段；通过图2（d）可看出第二级消力池内水跃消能较为充分，水流进入消力池段即发生水跃，水流波动发生于消力池范围内，证明该段消力池内水流消能较为充分；通过图2（d）可看出第三级消力池内水跃发生于消力池前段，水流流入第三级消力池后，并未立即发生水跃，底部主流沿陡坡进入消力池内形成弱漩滚，水跃发生于消力池中部。

表1 不同工况下试验流速值与数值模拟计算流速值对比表

通过数值模拟所得成果提取沿程流速分析可知，水流流经各级陡坡内流速随流程的增加而增加，在各级消力池发生了不同程度的消能反应。在第一级陡槽末端泄处，流速达到最大值16.34 m/s，经第一级消力池消能后，流速降至4.84 m/s；在第二级陡槽末端泄处，流速达到最大值18.01 m/s，经第二级消力池消能后，流速降至3.27 m/s；同样在第三级陡槽末端处，流速达到最大值17.42 m/s，经第三级消力池消能后，流速降至4.42 m/s。经过流速云图及数据分析可以看出，第一级消力池由于池深过大的影响，水跃发生在陡坡泄流段；第二级消力池由于池深过大的影响，消力池内水深较大，导致流速较小；第三季消力池由于池深不足，水跃发生与消力池中部。

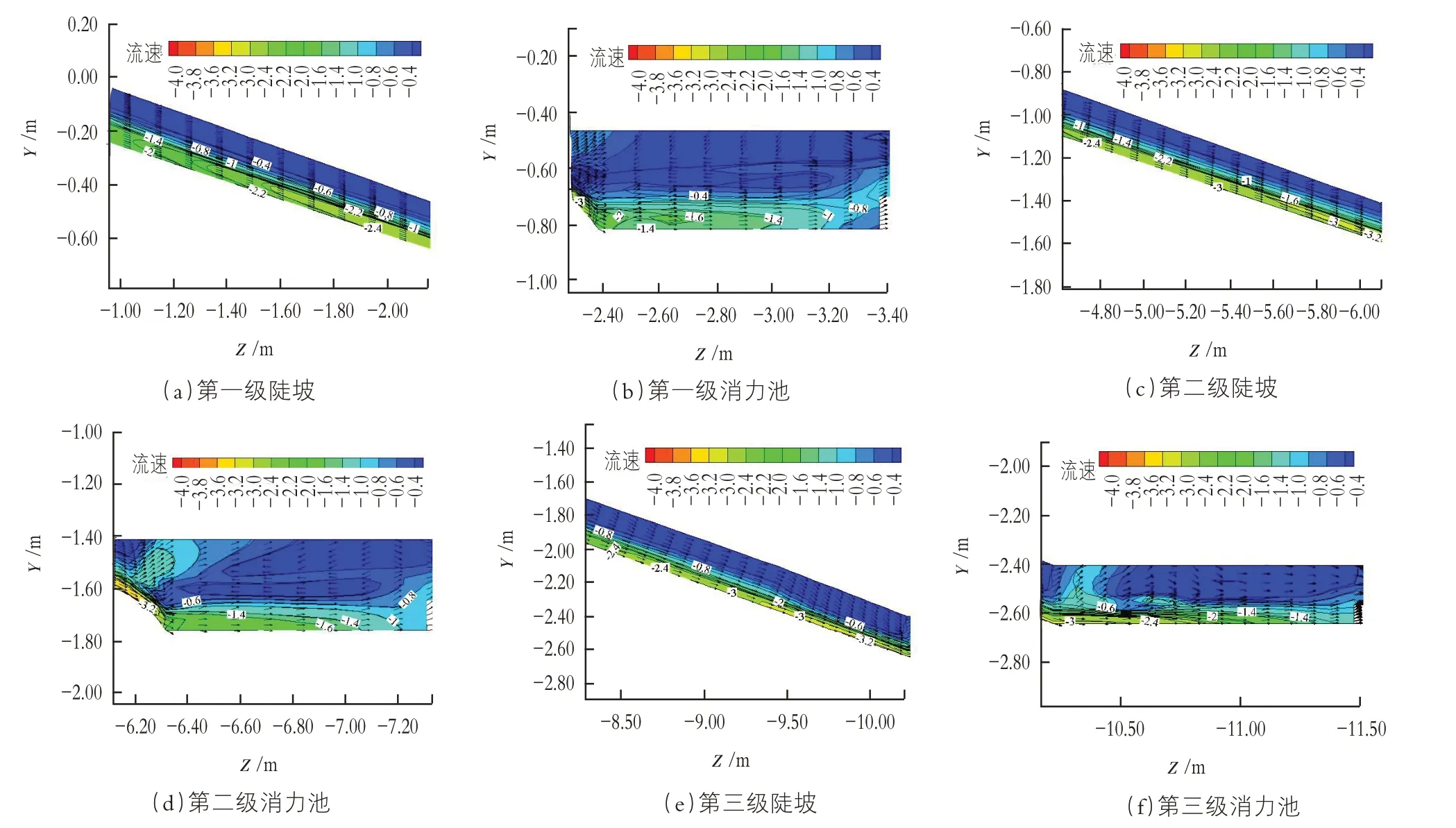
图2 速度矢量线云图

4 结语

通过建立多级泄水陡坡模型，运用双方程模型求解的计算方法，模拟计算校核工况下，多级陡坡内部水流运动状态，经过提取模拟计算得出的泄水陡坡内部水气两相流云图、流速矢量线云图分析可知得出：多级泄水陡坡消力池可满足现阶段消能目的，通过多级消力池可达到多级消能目的；根据数值模拟分析，该模型第一级消力池、第二级消力池池深过大，导致第一级消力池水跃发生于陡坡末端，第二级消力池内部水流流速较小；第三季消力池池深略小，导致水跃发生靠后，可将消力池池深加大，或将消力池池长加大。后续设计优化过程中，可根据本文所得结论，对消力池池深稍作优化。本文所得结论为后续优化多级陡坡消力池设计提供了理论依据。