拉线式桅杆的跨间稳定验算

张欣蓉 乐俊旺

(中广电广播电影电视设计研究院，北京 100045)

0 引言

拉线式桅杆是高柔非线性的结构体系，稳定问题是主要问题。至今，桅杆的整体稳定计算尚停留在杆身分肢屈曲计算阶段，并非极限状态承载力的计算。本文介绍桅杆跨间稳定性的几种验算方法，通过工程实例予以比较。

1 工程概况

有一座高为235 m、边宽为1.5 m的拉线式中波桅杆，截面为三角形格构式钢管组合结构，5层纤绳，杆身设笼子，直径为10 m，由15根φ9.0 mm铜包钢绞线组成。该桅杆的格构式杆身单元节段长度为5.7 m，单斜杆体系，2个节间，主柱规格，第1跨～第3跨为φ159×14，第4跨～第5跨为φ159×10，斜腹杆为φ57×5，柱肢端部设连接法兰盘。该工程建成后，对该座桅杆进行跨间稳定性验算。

2 核算方法

由于拉线式桅杆计算采用的方法不同，桅杆跨间稳定性验算曾有以下几种方法。

1)近似法—简支梁法。

假定桅杆纤绳结点为铰接，且将各跨横向风载换算为均布荷载，则各跨最大弯矩发生在跨中，即：

(1)

其中，qk为均布荷载，qk=βAkWk,β为风振系数,Ak为挡风面积,Wk为计算风压；lk为计算跨长。

作为压弯构件，考虑轴向力的影响，跨中最大弯矩应为：

Mmax=AuM0

(2)

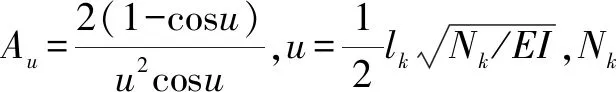
则跨间的整体稳定性：

(3)

其中，A为杆身毛截面面积；W为杆身毛截面模量；φ为轴心受压构件的稳定系数，由换算长细比(λ0)确定。

在一个跨间内，尚需验算轴向力最大截面的整体稳定性：

(4)

其中，Nmax为最大轴向力；M为相应于最大轴向力截面的弯矩。

按照有关规范标准，本例稳定验算计算见表1。

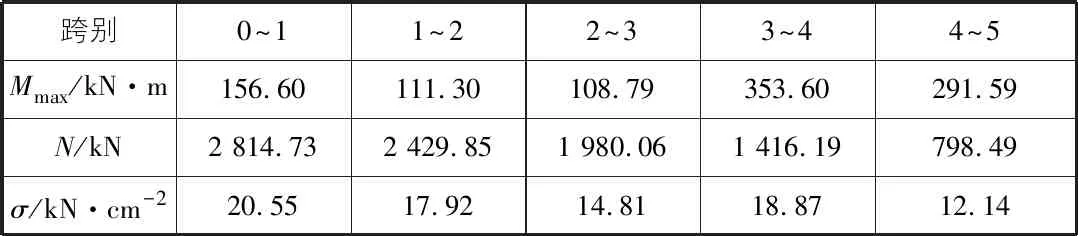
表1 简支梁法计算结果

2)弹性支座连续梁法。

用弹性支座连续梁法求得桅杆的支座弯矩Mk-1,k后，即可求得跨间的最大弯矩：

(5)

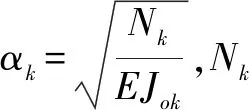
式(5)中Mmax的位置x值，可用式(6)求得：

(6)

其中，A=αklk。

跨间的整体稳定性计算同式(3)和式(4)。

也可用连梁法求得的支座弯矩Mk、位移Yk以及上下端的轴向力Nk、均布荷载qk等作用下，用简支梁法求出跨间Mmax及其位置。

计算结果见表2。

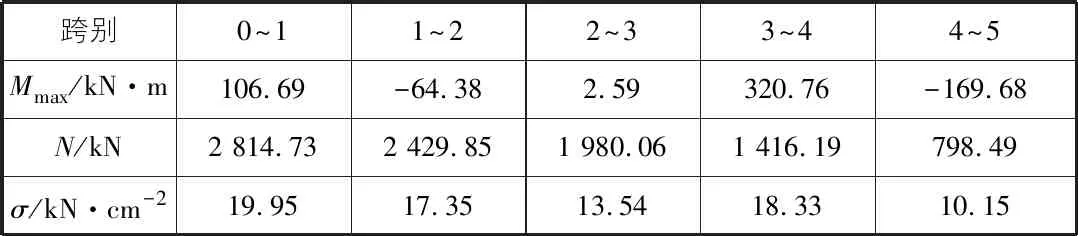
表2 弹性支座连续梁法计算结果

3)按格构式偏心受压构件计算跨间的整体稳定性(GYJ 1—84钢塔桅结构设计规程)。

(7)

其中，φb为格构式偏心受压构件在弯矩作用平面内的稳定系数，按换算长细比(λ0)和偏心率查得。其中偏心率：

(8)

其中，M为构件全长中间1/3长度范围内的最大弯矩，但不小于构件最大弯矩的一半;x0为从y轴到压力最大肢的轴线间距离和至腹板间距离的较大者;Iy为y轴的毛截面惯性矩；A为杆身毛截面面积。

计算结果见表3。

表3 按格构式偏心受压构件计算结果

4)按弯矩绕虚轴(x轴)作用的格构式压弯构件,其弯矩作用平面内的整体稳定性(GB 50017—2003钢结构设计规范)。

(9)

其中，N为所计算构件段范围内的轴心压力；A为杆身构件毛截面面积；φx为弯矩作用平面内的轴心受压构件稳定系数，由换算长细比(λ0)确定；βmx为等效弯矩系数，通常情况，βmx=1；Mx为所计算构件段范围内的最大弯矩。

W1x=Ix/y0。

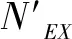
其中，λ0x为整个构件对x轴的换算长细比。

计算结果见表4。

表4 按弯矩绕虚轴作用的格构式压弯构件计算结果

3 比较分析

为便于比较，将以上验算桅杆跨间稳定性的四种方法计算结果汇总于表5。

表5 拉线式桅杆跨间稳定性σ验算比较 kN/cm2

总的来说,跨间稳定性的四种验算方法计算结果比较接近,唯简支梁法的计算，丢失了通常发生在支座上的最大弯矩,但根据计算经验，当杆身截面宽度与跨长的比值较小和结点变位线接近直线时，按简支梁计算所得的最大跨中弯矩，要大于按弹性支座连续梁计算所得的支座弯矩,因此，按简支梁法的计算值相对偏大。图1为四种方法所得计算值的比较曲线。

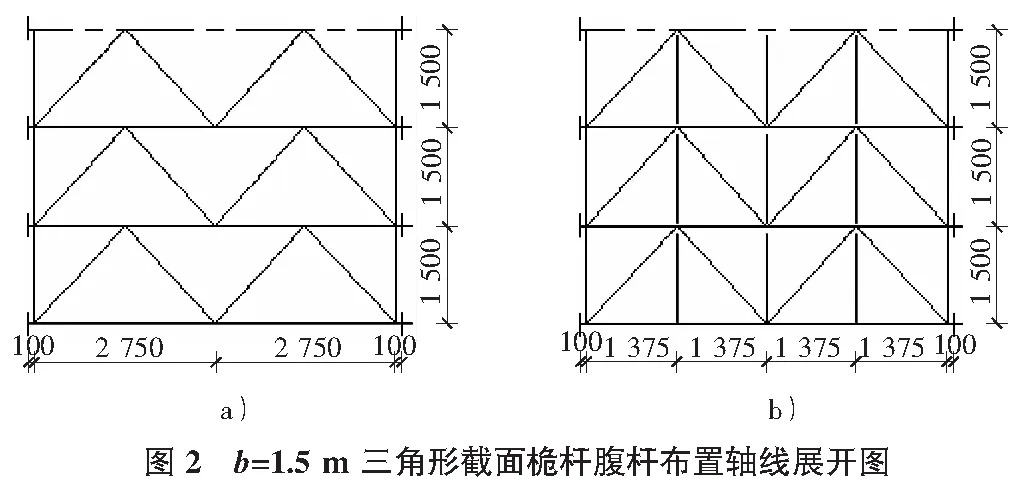
不论用哪种计算方法,该工程的跨间稳定性均超值,尤其第1跨、4跨,超值20%。原因在于边宽1.5 m格构式杆身采用单斜杆式腹杆导致偏心受压的主柱单肢过长(见图2a))。因偏心受压的主柱单肢过长、稳定性不够而产生的压弯变形,靠人工调直的办法是无济于事的，治标不治本，后来增设了横杆(见图2b))，缩短了主柱的计算长度，经改进后的边宽1.5 m桅杆定型设计，再用于工程，就消除了这种压弯变形现象，保证了结构的稳定性。

由图1σ值曲线可见,第4跨的σ值产生特变,原因在于主柱规格由第1跨～第3跨φ159×14，改为第4跨～第5跨φ159×10，变化太快,若第3跨，4跨改为φ159×12,第5跨及悬臂段为φ159×10，受力状况就会改善了。

4 结语

拉线式桅杆跨间稳定性的四种验算方法都是可行的,所得应力值,简支梁法最大,压弯构件法次之,连续梁法第三,偏心受压法最小,之间相差仅在1.0 kN/cm2左右。在工程设计中,桅杆计算通常采用弹性支座连续梁法,跨间稳定性验算可以满足要求。