对恒星发光规律的关联性探究

中国重庆市长寿第一中学校 重庆 401220

1 麦克斯韦速率分布函数与普朗克黑体辐射定律的相似性

我们从分布函数上可以直观看出二者具有高度相似性(图略),下面本文从理论上进行比较分析:

麦克斯韦速率分布函数为f(v)＝d N/(Ndv)＝4π[m/(2πk T)]1．5v2e[－mv2/(2kT)]。

普朗克黑体辐射定律I＝2hν3/[c2(ehν/kT－1)],而 ρv＝8πhν3/[c3(ehν/kT－1)]。

1．1 能量分析 假设一对正负电子湮灭产生一对光子,不考虑正负电子的静能,有2×1/2mv2＝2hν,则ν＝mv2/(2h)。我们假设恒星表面的正负电子满足理想分子麦克斯韦速率分布律。

1．1．1 从热力学角度的能量分析

根据前面的公式有d N＝N4πv2[m/(2πk T)]1．5e[－mv2/(2kT)]dv,则有

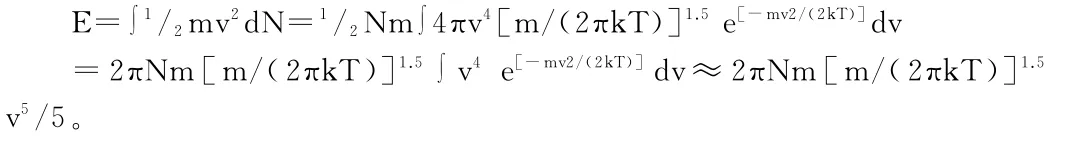
1．1．2 从量子力学角度的能量分析

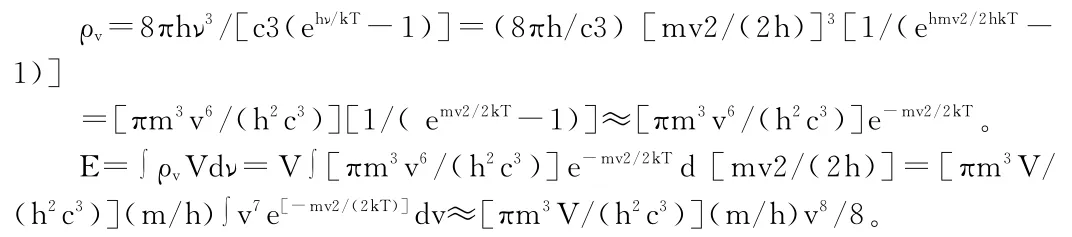
1．2 公式的整合 根据上述推导公式有2πNm[m/(2πk T)]1．5v5/5＝πm3V/(h2c3)(m/h)v8/8,变形得 m3V v8/(8h3c3)＝2N v5/5[m/(2πk T)]1．5,即 Vv3/(8h3c3)＝[2N/(5m3)][m/(2πk T)]1．5。由理想气体克拉伯龙方程p V＝NRT/NA得V＝NRT/(NAp),V2＝ [NRT/(NAp)]2,而前式两边平方得 V2v6/(64h6c6)＝N2/(50m3π3k3T3),代入上式变形得N2R2T2v6/(64h6c6N2Ap2)＝ N2/(50m3π3k3T3),故 有25m3v6π3k3R2T5＝32N2Ah6c6P2。又因为 k＝R/NA,则上式变形为25m3v6π3k5T5＝32h6c6p2。考虑到高温的正负电子气对应的平均动能Ek＝mv2/2＝3k T/2,有 mv2＝3k T,代入前式得675π3k8T8＝32h6c6p2,即

1．3 推论 基于前面的公式675π3k8T8＝32h6c6p2,而p V＝nRT＝(N/NA)RT＝Nk T,有p＝Nk T/V,近似认为N不变代入前式得出675π3k8T8＝32h6c6(Nk T/V)2,变形得675π3k6T6V2＝32h6c6N2,有 VT3＝C(C是近似定值)。

2 对恒星发光的科学建模

2．1 理论建模 诸如太阳之类的恒星处于主序星时期,对应发生的热核反应可以简化为:

2．2 对太阳发光中湮灭反应的能量占比的估算 对于氢的聚变反应:mp＝1．007825u,me＝0．0005486u,mα＝4．00260u,△m＝4mp－mα－2me＝0．0276028u;而对于一对正负电子湮灭发生的反应:△m′＝2me＝0．0010972u。由狭义相对论质能方程△E＝△mc2得出,在忽略正负电子的初动能的情形下,湮灭反应的能量占比为η＝2△m′/(△m＋2△m′)×100%＝7．36445%。

2．3 能量建模 考虑到正负电子的初动能Ek＝mev2/2,而对电子,考虑所受到的太阳的万有引力作用,有

换一个思路,从热力学理论角度看,考虑是高温电子气体,则由麦克斯韦分子速率分布律得出:

这充分说明前面的建模是成功的。

具体计算式为:2 mev2/2＋2mec2＝2ahν＝2ahc/λ(a为产生光子的对数),则

10－6/(6．62606957×10－34)＝0．2267×106对。而太阳中心的温度为1500万K＝2600 T,则根据观测数据,到达地球的太阳光谱的波长范围大致为0．15μm～4．0μm,我们取v为4．368×105m/s～2．1324×107m/s,波长λ取0．15μm～4．0μm,代入2 mev2/2＋2mec2＝2ahν＝2ahc/λ中分别计算出a值存在一定的波动范围。

产生这种误差的原因在于太阳发光湮灭的能量占比不足8%,主要为热核反应中产生的能量促使大量的电子发生辐射跃迁发光,能量分析几乎等同于(2 mev2/2＋2mec2)÷7．36445%＝N′hν,N′是4个质子聚变和其后的湮灭反应产生的总光子数(即后面的4b),这与文章最初的分析基本相吻合。

2．4 太阳光谱能量分布函数假设 我们基于上述的大量分析进行如下假设:

ρv′＝ρv－[M/(4πR3/3)]mec2/(4bmH),ρv＝8πhν3/[c3(ehν/kT－1)],M、R分别为太阳的质量和半径,me和mH分别为电子和氢原子质量,b为待定系数。这个公式可以借助超级计算机模拟界定b值,b值与a值以及恒星聚变和湮灭的能量占比有紧密的关联,这需要借助超级计算机做精准建模和仿真计算得出数据。大致为4a÷7．36445%＝4b,即a≈7．36445b%＝0．0736455b,b≈13．5785622a。

2．5 几个关联的推断

(1)675π3k6T6V2＝32h6c6N2,有VT3＝C(C是近似定值),N为恒星的氢原子数。

如果忽略N的衰减(N的精准值可以用超级计算机计算出来),则有VT3＝(4πR3/3)T3＝C,有 RT＝C′。

太阳大约在50亿年后先脱离主序星的行列进入亚巨星阶段,持续约1亿年;之后转入红巨星阶段,核心出现简并氦核,持续10万年。之后出现氦闪,进入不稳定期,大约持续5000万年;最后约有1万年的渐进巨星阶段;后进入白矮星,再到黑矮星。

太阳在转入红巨星的时候会有多大的半径?官方理论评估将吞噬现有地球轨道半径,那时的地球随着太阳质量的不断衰减运行轨道会向外退行0．9亿km。是这样吗?

根据观测数据,到达地球的太阳光谱的波长范围大致为0．15μm～4．0μm,理论评估那时的太阳光谱波长范围略微放大(见后)。而可见光波长范围是0．39μm～0．78μm,0．8μm～4．0μm 是红外线波段。基于公式RT＝C′,hν＝hc/λ＝0．5mev2,v2＝3k T/me,太阳光谱波长λ会放大为现有的2－26倍,太阳表面的温度T减小为现有的0．5－1/26(即2885K－222K),太阳半径变为现有半径的2－26倍(约为140万km－1820万km)。很显然官方理论严重错误。如果不考虑地球轨道外移因素,则地表温度约为150K－11．3K,会导致地球人类过早灭绝。

(2)太阳达到地球的光谱能量曲线ρv′＝ρv－[M/(4πR3/3)]mec2/(4bmH),ρv＝8πhν3/[c3(ehν/kT－1)],M、R分别为太阳的质量和半径,me和mH分别为电子和氢原子质量,b为待定系数,a≈7．36445b%＝0．0736455b,b≈13．5785622a。

设定b为定值,随着时间的流逝,太阳半径R逐渐变大,而太阳质量M的衰减并不显著,由数学知识分析得出,ρv′＝0求解出来的太阳到达地球的光谱ν对应频段放大,对应的波长范围λ也会有增大。用极限法分析得出处于黑矮星阶段的太阳就是绝对黑体。

(3)湮灭弹产生反应的能量阀域

ρv′＝ρv－[M/(4πR3/3)]mec2/(4bmH),ρv＝8πhν3/[c3(ehν/kT－1)],M、R分别为湮灭弹的质量和半径,me和mH分别为电子和氢原子质量,b为待定系数,b≈13．5785622a。

令ρv′＝0,求出ν的最小值,且hν＝0．5mv2＝1．5k T,解出 T即可,而M∝R,这决定了湮灭弹的爆炸威力。

3 前瞻性探究

3．1 恒星量子引力场论的开创 广义地说,恒星量子引力场论将涉及到新一轮的重大基础理论的变革和创造,涵盖热力学与统计物理学、大数据分析、仿真模拟、相对论、引力红移、量子力学和牛顿力学及光学、原子物理学等方面的综合理论。

3．2 恒星量子引力场论将极大地推动人类的科技进步 这个理论将引领人类合理有序地操纵恒星能源,用湮灭原理去开发新兴核能,使得人类文明等级发生飞跃性的进步。

3．3 自然科学理论创新进入新时代 人类顶尖科学家团体共同合作,建立精准的恒星发光光谱能量分布解析式,借助超级计算机进行仿真建模,必将急速推动世界自然科学理论的伟大革新进程!

3．4 引力红移 假设一个光子的动质量为m(r),它从距离恒星球心r处沿着径向远离dr的过程中万有引力对其做负功导致其动质量的减小量为dm(r),则有微分方程:

3．5 引力场能量分布函数

为了使得研究简化,我们假定是一个孤立的巨大恒星置于宇宙中发光。下面我们界定它的引力场的能量分布函数。

我们把恒星视为绝对黑体,由斯忒藩－玻尔兹曼定律变形得P＝4πR σT4(R为星体半径,T为星体表面热力学温度),而P＝(d N)mc2/dt,则有dN＝4πR σT4dt/(mc2)。

所以在距离恒星球心r～r＋dr(r≥R)的球壳层中的引力场光子的能量分布密度为:

而在距离恒星球心r～r＋dr(r≥R)的球壳层中的引力场引力子的暗能量分布密度为:

对恒星r＜R时的能量分布探究暂略。

我感谢吴朋生(系我外侄)和民科吧里的弦中子(朱成明)、dym、bt教教主、端意_R_致格、陈彼方、羊歌乐等同志的帮助!

2020－07 －22 15:00