基于有限元软件自定义本构模型的膨胀土边坡降雨入渗分析

饶 鸿，王金淑，赵志明，吴 光，冯 涛

（1.西南交通大学地球科学与环境工程学院，四川 成都 610081；2.中铁二院工程集团有限责任公司，四川 成都 610081）

降雨引起土体强度变化是诱发边坡失稳的重要因素之一，研究降雨入渗动态过程中边坡稳定性的变化有重要现实意义[1]。降雨入渗过程中雨水浸润土体增加其重度，土体的含水量增加降低其基质吸力和抗剪强度[2]。降雨入渗过程中非饱和土的重度、强度、吸力等参数都与非饱和土的含水率或饱和度密切相关，探究降雨入渗对非饱和土边坡稳定性的影响规律，需要考虑非饱和土重度、强度参数等因素的变化。

近年来，学者们在滑坡机理分析中越来越多地考虑降雨条件下的岩土体参数变化，并取得了重要成果。Cai 等[3]分析了降雨条件下地下水位变化对非饱和土边坡的稳定性影响；韦立德等[4]提出了考虑渗流场与含水率变化的强度折减有限元算法，研发出三维强度折减有限元程序；陈善雄等[5]结合降雨入渗土体重分布饱和度对抗剪强度参数的影响，提出考虑水分入渗的非饱和土边坡稳定性分析方法；麻官亮等[6]以改进的三维极限平衡法模型为基础，建立了边坡三维滑裂面的搜索模型；李宁等[7]应用ABAQUS 有限元软件的二次开发技术，结合Geostudio 软件建立了降雨条件下边坡有限元强度折减计算平台；王协群等[8]提出了基于变模量的弹塑性强度折减方法；李绍红等[9]编制计算程序，探究不同降雨类型下浅层边坡的稳定性变化规律；张晨阳等[10]应用Geostudio 软件分析了两种降雨工况下残积土边坡的稳定性特征。上述方法都是通过自编程序或软件的二次开发技术实现了对非饱和土边坡的稳定性分析，取得了重要进展，但难度较大。

ABAQUS 有限元软件是岩土分析中应用较广的专业性软件。软件内置的python 语言和Fortran 语言可用于软件的二次开发及子程序编写；在ABAQUS 有限元软件中，为了实现岩土体参数与某变量的函数关系，可以将该变量定义为场变量（FIELD），应用命令流或内置语言代码实现函数关系，为本文的数值模拟提供可行性技术支持。

对于大多数数值分析软件而言，无法直接将非饱和土的含水率或饱和度同土体重度、抗剪强度指标等参数建立联系，无法准确地模拟降雨过程边坡参数的动态变化对稳定性的影响。为了突破这一局限性，本文以贵广（贵阳—广州）高铁贵州段尖山营地区的膨胀土为研究对象，推导出适用于尖山营地区膨胀土的抗剪强度公式；基于ABAQUS 有限元软件的二次开发技术，编写USDFLD 子程序实现了土体含水率变化引起的膨胀土重度、抗剪强度的动态变化，探索饱和-非饱和渗流条件下考虑多种影响因素的边坡变形规律及稳定性，实现降雨入渗对非饱和土边坡影响因素的模拟，为降雨 引发滑坡的机理研究提供参考。

1 尖山营膨胀土的抗剪强度分析

国内外众多学者对非饱和土的抗剪强度理论做出大量研究，在经典饱和土力学的基础上提出了不同的非饱和土抗剪强度理论模型，常见的有Bishop 理论[11]、Fredlund 理论[12-13]、卢肇钧吸附理论[14]等。这些理论都肯定非饱和土的基质吸力对抗剪强度产生的贡献，证实了由于基质吸力产生的强度是非线性变化的。而基质吸力与非饱和土的含水率是密切相关的，土水特征曲线是基质吸力与含水率的关系曲线，表征两者的关联。缪林昌等[15]、郭倩怡等[16]通过直剪试验探究了膨胀土强度与含水量或基质吸力的关系，提出了以含水率为参数的膨胀土抗剪强度公式。本文也是基于文献[15]的思想，将尖山营地区的膨胀土作为研究对象，通过室内直剪试验获得了不同含水率条件下膨胀土的抗剪强度，建立膨胀土的抗剪强度指标与含水率的关系，将Fredlund 提出的非饱和土抗剪强度公式修正为以含水率为变量，推导出适用于尖山营膨胀土的抗剪强度公式。

根据钻探调查，贵广高速铁路位于贵州段贵定县尖山营地区发育有膨胀岩土层，尖山营膨胀土呈灰色、灰白色、灰黄色，块状，硬塑-坚硬状态，矿物成分主要为伊利石、石英，黏粒含量较少。该地区属于亚热带季风气候，区域膨胀土历经雨季吸水膨胀、旱季脱水收缩的反复过程，相当长时间内处于非饱和状态。

首先配置相同干密度（ρd=1.6 g/cm3），初始含水率为0%、8%、10%、12%、14%、16%、18%、20%、22%、30%的膨胀土样，同一含水率配置3组试样（1组测量试验和2组平行试验），将膨胀土样分别倒入制土设备应用静力法压实制备成标准环刀试样（图1）。采用应变式直剪仪以0.8 mm/min 剪切速率进行快剪试验，根据试验结果计算出不同含水率的膨胀土样对应抗剪强度指标（图2试验数据点）。

图1 尖山营膨胀土标准环刀试样Fig.1 Standard ring cutter sample of the Jianshanying expansive soil

对膨胀土不同含水率的抗剪强度指标进行回归分析，建立非线性曲线拟合曲线模型（图2拟合曲线），推导出尖山营膨胀土的抗剪强度指标与含水率的拟合公式为：

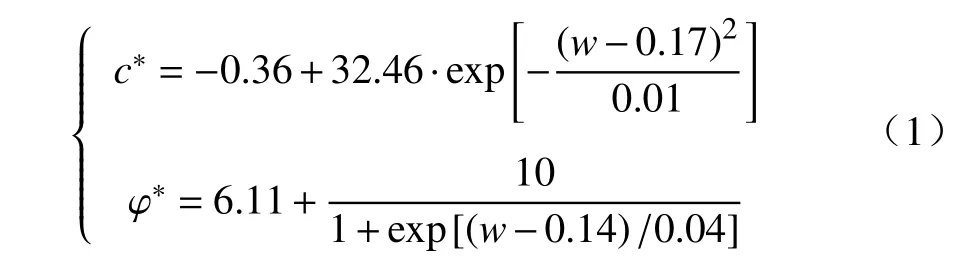
式中：c*-总黏聚力/kPa；

φ*-总内摩擦角/（°）；

w-含水率。

由图2可知，尖山营膨胀土的抗剪强度与含水率密切相关：伴随土体含水率增加，黏聚力呈先增后减的趋势，最优含水率对应的黏聚力值最大；内摩擦角逐渐减小，总抗剪强度降低。

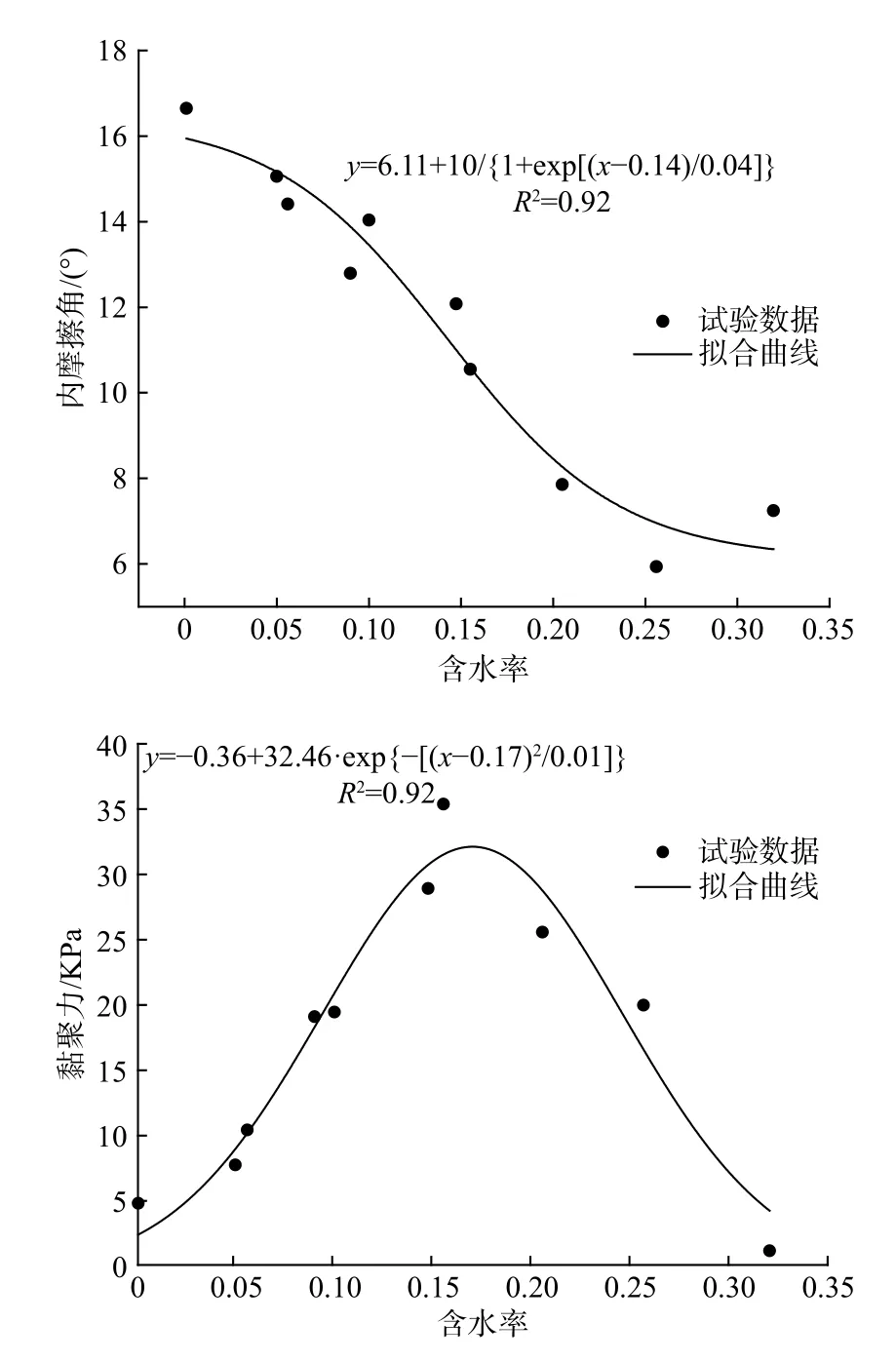
图2 抗剪强度指标拟合曲线Fig.2 Fitting curve of the total shear strength index

Fredlund 等在1978年建立了非饱和土的抗剪强度理论模型，提出双变量抗剪强度公式[12]：

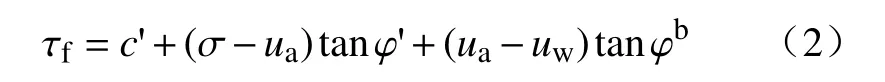
式中：τf-抗剪强度/kPa；

ua-孔隙气压力/kPa；

uw-孔隙水压力/kPa；

c'-有效黏聚力/kPa：

φ'-有效内摩擦角/（°）

(σ-ua)-净法向应力/kPa；

(ua-uw)-基质吸力/kPa；

φb-受基质吸力影响的内摩擦角/（°）。

根据Fredlund 抗剪强度理论，非饱和土抗剪强度中有效黏聚力为常量，土体的抗剪强度受净法向应力和基质吸力两个变量共同影响，基质吸力产生的吸附强度是非线性变量[13]。研究表明：非饱和土的基质吸力随含水率变化而变化，受基质吸力影响的抗剪强度可以考虑为含水率变化引起基质吸力变化，进而影响了土体的抗剪强度。根据尖山营膨胀土的直剪试验结果可知土体抗剪强度指标是随含水率变化的，故而将有效黏聚力和吸附强度叠加起来，引进广义黏聚力概念（式3），用总黏聚力表征受基质吸力影响下黏聚力对抗剪强度的贡献[17]。

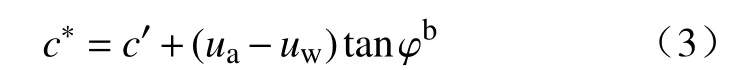
式中：c*-总黏聚力/kPa。

将Fredlund 非饱和土抗剪强度公式修正为：

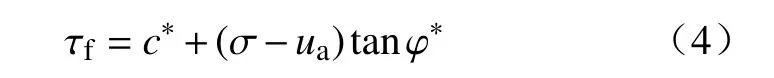
再结合土体的抗剪强度指标与含水率的拟合公式（式1），将式（4）中的抗剪强度指标c*、φ*用含水率表示，推导出以含水率为变量的尖山营膨胀土抗剪强度公式：

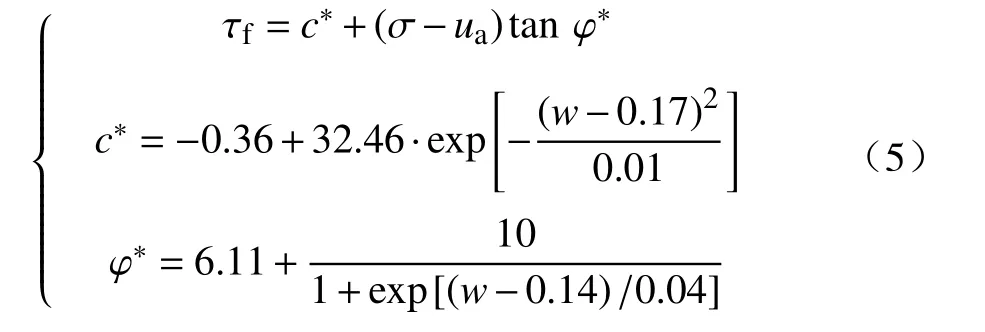
由式（5）可知，膨胀土的抗剪强度指标不再是常数，而是与含水率有关的变量。雨水渗入膨胀土边坡中，膨胀土的抗剪强度会伴随含水率变化而改变，实现了考虑抗剪强度影响因素的模拟，可供实际工程参考。

2 ABAQUS 有限元二次开发原理

2.1 饱和-非饱和渗流方程

降雨在非饱和土中的渗流满足质量守恒定律，达西定律也同样适用于非饱和土渗流分析[18]。以达西定律为基础结合渗流过程中流体质量守恒推导出以基质势为因变量的渗流控制方程[19]。

饱和-非饱和渗流问题的基本方程[7]：

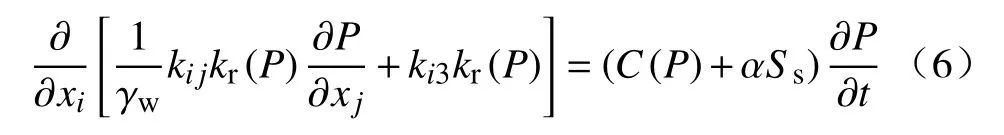
式中：xi、xj-i、j方向坐标；

ki j-饱和渗透张量；

ki3-饱和渗透系数；

P-孔隙水压力/kPa；

kr(P)-相对渗透系数；

C（P）-容水度；

γw-水体重度；

t-时间变量；

Ss-单位贮存量；

α-饱和状态参数，α=0时计算非饱和渗流，α=1时计算饱和渗流。

在ABAQUS 中非饱和土是多孔三相介质材料，需考虑土体中存在气体压力ua和液体压力uw。其有效应力原理同常规土力学的表达略有不同[20]：

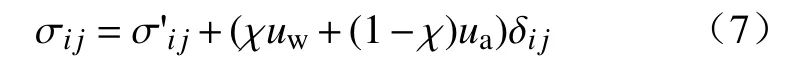
式中：σij-总应力张量分量；

σ'ij-有效应力张量分量；

χ-有效应力系数，一般取饱和度。

2.2 强度折减理论

在边坡稳定性分析中，假定用不同的折减系数对抗剪强度指标进行折减，人工削弱土体的抗剪强度，使单元应力达到屈服或超出屈服面，边坡产生塑性变形，当其内部形成连续塑性贯通面或特征部位产生突变位移，表征边坡失稳破坏。本文应用ABAQUS 软件定义折减系数为场变量，实现边坡的强度折减，计算边坡稳定系数。

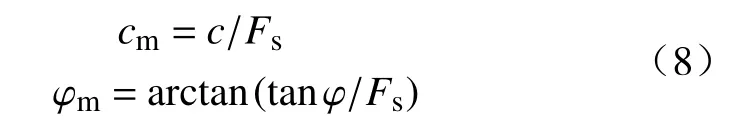
式中：Fs-强度折减系数；

c、φ-实际抗剪强度指标；

cm、φm-人为折减后的抗剪强度指标。

2.3 有限元二次开发思路

在降雨过程中，膨胀土的重度、抗剪强度指标是伴随含水率或饱和度的变化而变化的，而ABAQUS 有限元软件中只有饱和度和孔隙比参数。本文应用含水率公式求解出膨胀土的含水率，通过Fortran 语言在子程序中将含水率定义为场变量：首先利用内置“CALL GETVRM”命令导出材料的饱和度与孔隙比参数数据，再应用含水率公式计算出含水率w，将计算结果定义为场变量，即“FIELD（1）=w”；通过降雨过程中每一时间增量步的迭代计算，可求解出降雨过程中土体含水率、饱和度及孔隙比的实时数据；结合尖山营膨胀土抗剪强度变化规律（式5），应用ABAQUS 有限元软件内置Fortran语言将膨胀土的抗剪强度指标随含水率的拟合公式编写成代码导入到USDFLD 子程序中；再导入折减系数定义其为场变量，做降雨过程边坡稳定性分析，分析降雨过程边坡的稳定系数的变化规律。

二次开发思路如下：

（1）应用ABAQUS 有限元软件内置Fortran 语言，编写含水率公式代码，求解出每一时间增量步对应的实时含水率，即膨胀土的过程含水率。

（2）将过程含水率定义为场变量，根据尖山营膨胀土的抗剪强度公式编写成USDFLD 子程序，实现土体抗剪强度指标与场变量的拟合关系，验证通过子程序。

（3）建立膨胀土的边坡模型，在ABAQUS 软件中的Property 模块设定土体重度参数随场变量的增量值，进行降雨入渗分析。

（4）提取降雨过程每一时间步的含水率及其分布云图，迭代计算出每一时刻土体的综合抗剪强度值，导入折减系数场变量进行边坡强度折减分析，获得降雨全过程的边坡稳定系数曲线。

计算流程见图3。

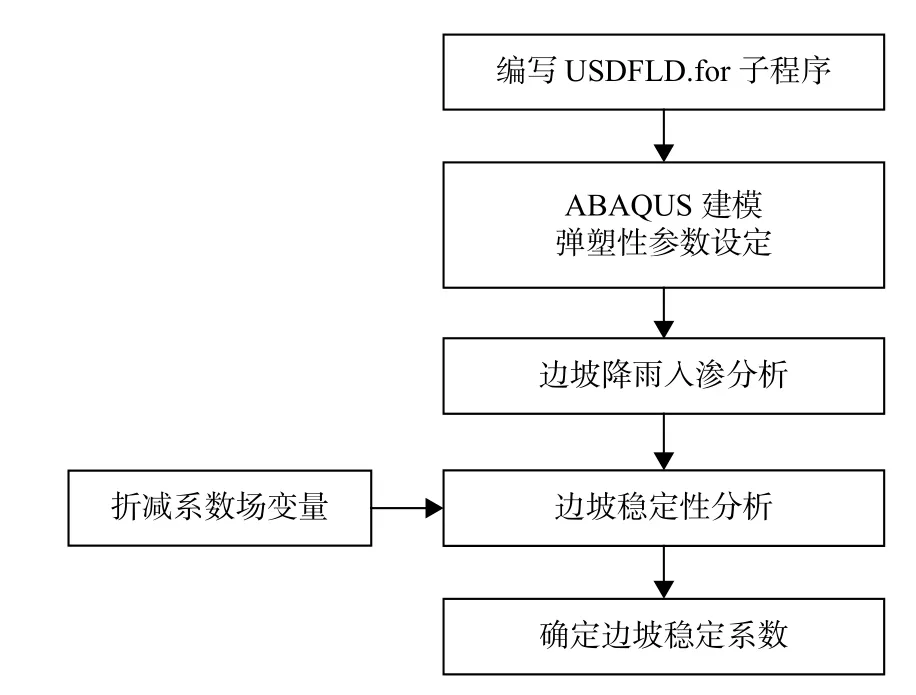
图3 计算流程图Fig.3 Calculation flow chart

3 有限元计算实例

3.1 边坡计算模型

边坡计算模型为膨胀土匀质边坡，边坡有限元模型及几何尺寸如图4所示。底面为水平向竖向约束边界，侧面为水平向约束边界，其余为自由边界。左侧边界地下水水头为10 m，右侧边界地下水水头为8 m，顶面边界为降雨入渗边界，降雨全部入渗。为了充分考虑降雨影响，延长降雨历时使膨胀土能达到饱和状态，土体抗剪强度衰减至极限状态。取降雨强度为0.01 m/h，降雨历时24 h。材料为理想弹塑性模型，遵循Mohr-Column 强度准则。具体材料参数见表1。

3.2 土水特征曲线

首先配置不同初始含水率的膨胀土样，将其制备成标准环刀试样，采用滤纸法测量出不同含水率土样对应的基质吸力值（图5试验数据点），结合Van-Genuchten[21]数学模型分析体积含水率与基质吸力的相关关系，计算出Van-Genuchten模型的参数（表2），得到体积含水率与基质吸力的拟合公式，拟合出尖山营膨胀土的土水特征曲线（图5拟合曲线）。

图4 膨胀土边坡计算模型Fig.4 Calculation model of an expansive soil slope

表1 土体材料参数Table1 Soil material parameters

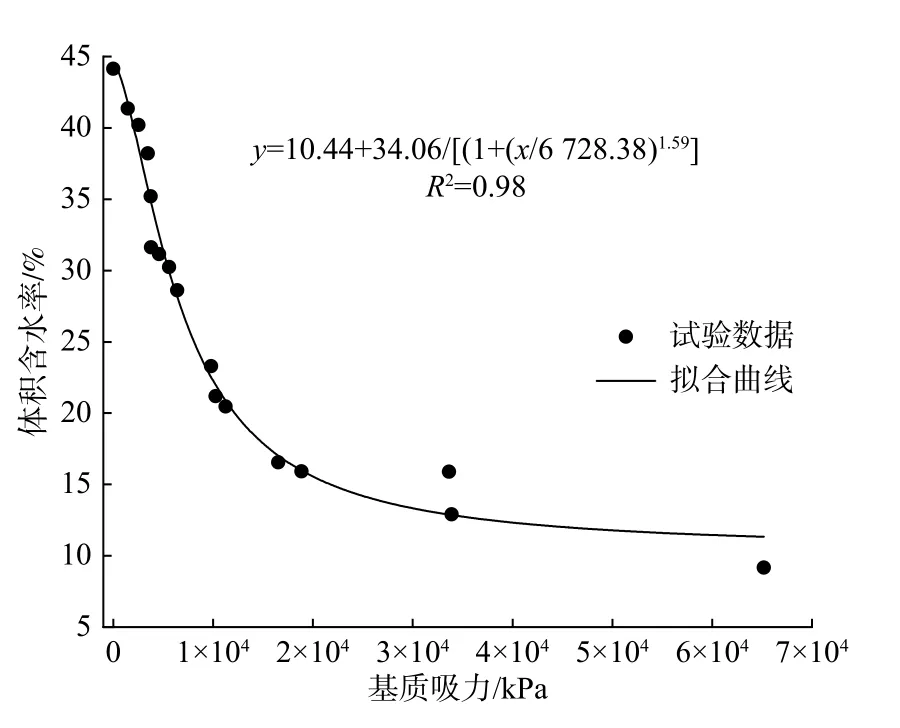
图5 土水特征曲线Fig.5 Soil water characteristic curve

表2 Van-Genuchten模型参数Table2 Van-Genuchten model parameters

3.3 膨胀土重度

在降雨入渗非饱和土边坡过程中，土体受水浸润，地下水位以上非饱和土重度发生变化，非饱和土湿重度随含水率增加而增加。

式中：w-含水率；

γd-干重度/（kN·m-3）；

γw-湿重度/（kN·m-3）。

实现方法：将含水率w定义为场变量，计算出不同含水率对应的湿重度，通过表格形式设定土体湿重度参数与含水率的对应值。

3.4 尖山营膨胀土抗剪强度

降雨渗入非饱和土边坡，土体吸水抗剪强度会降低（式5）。

实现方法：将含水率w定义为场变量，将尖山营膨胀土抗剪强度公式编写成Fortran 语言代码，导入到USDFLD 子程序中，实现c*、φ*指标与场变量的拟合。

4 计算结果分析

同一降雨工况下，分别计算考虑土体重度、抗剪强度变化（导入子程序）和不考虑土体参数变化（不导入子程序，将膨胀土参数取为定值）的边坡稳定性，对比数值模拟结果，探究两种情况下膨胀土边坡变形规律及稳定性特征。

4.1 降雨入渗分析

在ABAQUS 软件中导入USDFLD 子程序，进行膨胀土边坡降雨入渗分析，取边坡临空面顶部（A点）和底部（B点）探究边坡不同位置的雨水入渗规律。图6为降雨全过程坡顶、坡脚土体含水率曲线：土体含水率随降雨历时逐渐增大，坡顶处初始含水率低，含水率缓慢递增且增幅较大，降雨15 h 左右土体达到饱和含水率（图6饱和点）；坡脚处初始含水率高，含水率率先增加至接近饱和，降雨20 h 左右土体达到饱和含水率（图6饱和点）；降雨后期土体含水率仍保持递增趋势。表明雨水向边坡内部渗流中，首先会在坡脚处汇集，坡脚土体含水率先接近饱和，土体吸水浸润后孔隙比增大，强度降低而变形增大，故降雨后期含水率又持续增加，雨水逐渐向内部渗流。

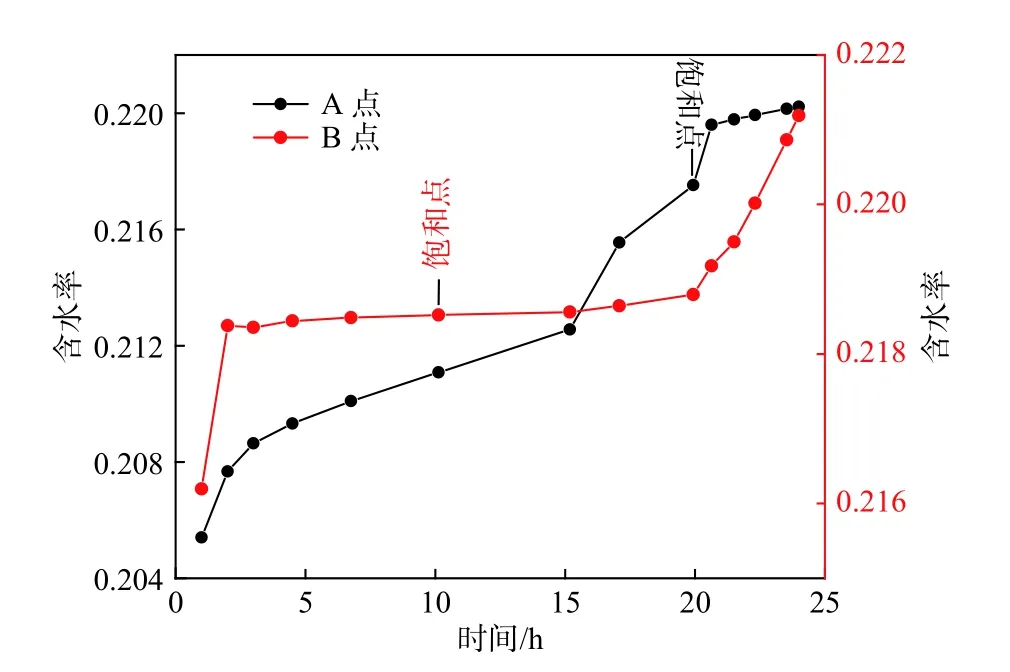
图6 降雨过程含水率曲线Fig.6 Moisture content curve during rainfall

对比降雨前后含水率分布图（图7）：降雨前初始水位以下为饱和区，孔压为正，土体饱和，初始水位以上为非饱和区，孔压为负，含水率由水位向坡顶递减，土体非饱和；降雨后雨水入渗浸润土体，导致地下水位抬升，边坡内部非饱和区逐渐减小，饱和区逐渐扩大并发展至整个边坡，雨水逐渐向内部渗流，在边坡内部某深度发育出圆弧形的水分汇集区（图7红色区域显示为最大含水率，水分最集中），从坡脚贯通至顶面。结合膨胀土抗剪强度与含水率的拟合关系分析，该区域土体吸水后强度软化最严重，抗剪强度较周围土体处于较低值，土体易产生相对大的变形，可能发育成滑动面。

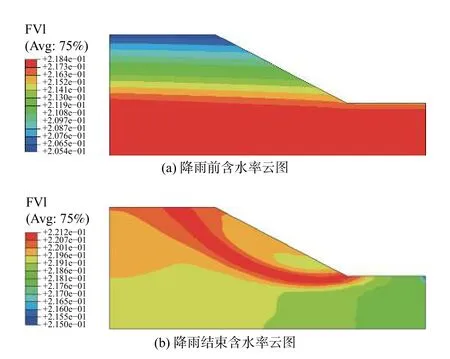
图7 降雨前后含水率云图Fig.7 Moisture content nephogram before and after rainfall

4.2 位移场分析

取坡脚（图5B点）土体为位移监测对象。由降雨过程土体位移曲线及总位移矢量图（图8）可知，考虑土体参数变化的影响时（图8a），膨胀土在雨水入渗后会产生变形，土体位移伴随降雨时间持续增大。根据位移曲线斜率变化，可将土体位移曲线分为稳定变形阶段和非稳定变形阶段：（1）稳定变形阶段，曲线较平缓、斜率较小，土体位移很小，伴随降雨持续变形缓慢增大，以小变形为主；（2）非稳定变形阶段，曲线较陡峭斜率较大，位移曲线出现显著拐点后，水平、竖向位移同步猛增，位移变化率较大，降雨结束后水平、竖向位移数量级较大且水平位移大于竖向位移。表明土体受降雨影响产生了不可逆的大变形，可由位移曲线拐点大致判断边坡失稳时间点；边坡内部发育圆弧形滑动面，土体顺滑动面向坡外滑移，中下部土体以水平变形为主，上部土体以竖向变形为主，总体位移数值较大，表明持续降雨引发边坡整体失稳，中下部先产生大变形，诱使上部土体下滑，具备典型牵引式滑坡特征。边坡内部滑动面位置与水分汇集区基本一致，说明雨水入渗过程会由坡脚向某区域汇集，致使土体软化严重、强度降低，向坡顶发展至贯通，形成圆弧形滑面。

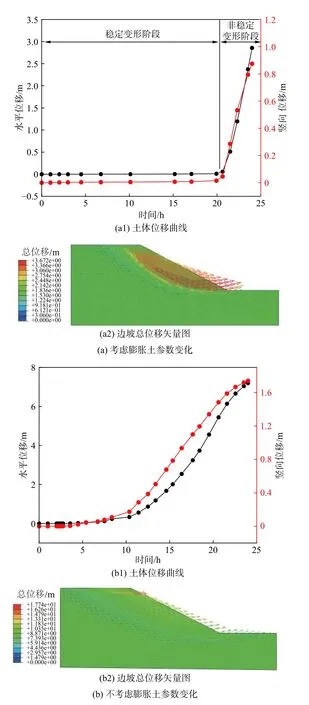
图8 土体位移曲线及总位移矢量图Fig.8 Soil displacement curve and total displacement vector diagram

不考虑土体参数变化因素时（图8b）：降雨过程土体位移伴随降雨历时递增，土体位移变化率由小到大缓慢增加，但土体位移曲线未出现明显拐点。降雨结束后总位移较大，水平位移远大于竖向位移，表明降雨引发边坡失稳破坏；边坡内部发育圆弧形滑动面，土体顺滑动面向外滑移，以水平位移为主，表明上部土体率先产生大变形，推移中下部土体向坡外移动，具备典型推移式滑坡特征。

综上所述，在降雨工况下，考虑土体重度、抗剪强度等因素变化时，边坡失稳的主因是雨水入渗后在坡内某区域汇集，使土体抗剪强度指标伴随含水率增加而减小，基质吸力减小且抗剪强度降低，引发牵引式滑坡；不考虑土体参数变化时，边坡失稳的主因是雨水入渗使地下水位抬升，边坡后缘水位高于坡脚水位，内部雨水向坡脚流动产生以水平向为主的渗流力且不断增大，土体基质吸力减小导致有效应力也减小，引发推移式滑坡。

4.3 膨胀土边坡稳定性评价

图9为膨胀土边坡的塑性贯通面示意图。考虑土体重度、抗剪强度等因素变化：雨水先在坡脚处汇集，故坡脚土体强度首先减小产生塑性变形，伴随雨水持续入渗，土体抗剪强度逐渐降低，塑性变形逐渐向内部发展；降雨21 h 左右，塑性变形延伸至坡顶形成贯通面，边坡失稳滑动，稳定系数为0.997，滑面形式为坡脚圆；降雨结束后，稳定系数为0.927。不考虑土体参数变化时：土体吸水后吸力减小，有效应力也减小，边坡土体受雨水入渗产生的渗流力作用有向坡外变形的趋势，伴随渗流力不断增大，有效应力不断减小，土体产生塑性变形并不断发展，降雨12 h 左右，塑性变形形成贯通面，边坡失稳滑动，稳定系数为0.994，滑面形式为中心圆，降雨结束稳定系数为0.845。

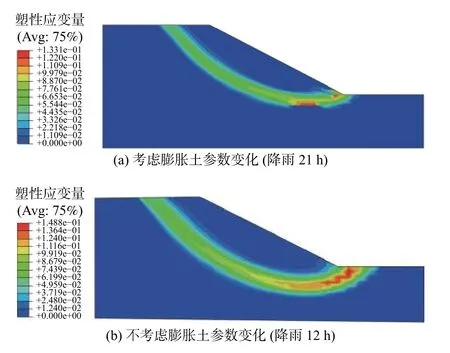
图9 边坡塑性贯通面示意图Fig.9 Schematic diagram of the plastic through surface in slope

降雨工况，导入子程序计算考虑了土体重度随含水率增加而增加，故而边坡稳定系数有所提高，计算稳定系数相对较大；不导入子程序计算将土体参数取为有效强度指标，其定值较小故边坡更易发生失稳破坏（表3）。这可能是两种情况下边坡失稳时间不同、稳定系数有偏差的原因。

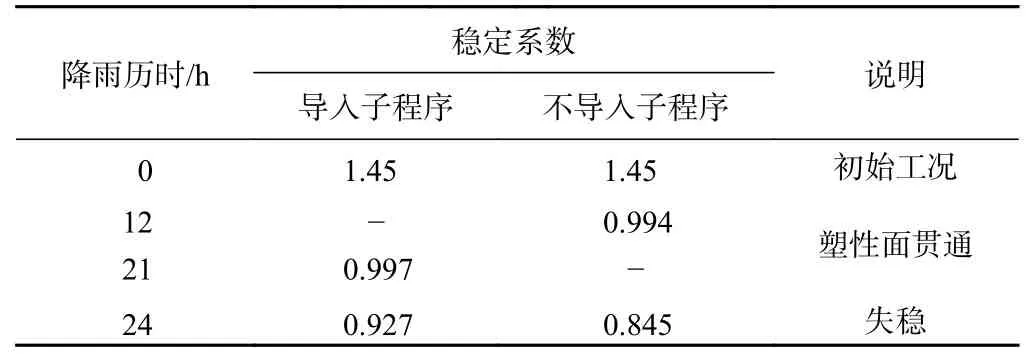
表3 边坡稳定系数Table3 Slope stability coefficient

5 结论

（1）尖山营膨胀土的抗剪强度与含水率密切相关：伴随土体含水率增加，黏聚力呈现先增后减的趋势，内摩擦角逐渐减小，总抗剪强度降低。

（2）持续降雨过程中，雨水首先在坡脚汇集再逐渐向边坡内部入渗，并在一定区域集中，降雨渗透区域土体软化，强度降低，塑性变形增大，逐渐发展贯通形成圆弧形滑动面，最终导致土质边坡发生牵引式滑动。

（3）基于二次开发技术成功实现了考虑膨胀土重度、抗剪强度指标伴随土体含水率动态变化的数值模拟，且经过与传统数值模拟对比，本文所提出的分析方法计算结果更合理，可应用于非饱和土边坡的稳定性研究分析。