基于栅格数据的最短路径分析
班国庆
(山西省测绘地理信息院第一测绘院,山西 太原 030002)
0.引言
起点和终点之间的距离衡量方式可以分为直线距离、成本加权距离、路径距离。直线距离表示研究点与其最近目标点之间的直接连线长度,无法反映出行的其他阻力、限制;成本相关的函数考虑成本,比如是不是应该避开河流,是不是要求距离较短,是不是要靠近主干道路,是否受地形影响;路径距离是在成本距离的基础上综合考虑表面距离、垂直方向上成本、水平方向上成本等三个方面。相关的研究有:张研[1]以晋陕豫黄河金三角3A级及以上景点为研究对象,基于GIS栅格成本加权距离法,从景点可达性时间、县域景点可达性、县域可达性的空间相关性三个方面对区域内的景点可达性进行了研究。李弘正[2]从系统整体性角度出发,以GIS空间分析技术为支撑,以无锡市堰桥镇为例,采用成本加权距离法进行交通可达性建模,定量分析了其与周边13个潜在客源地城市之间的交通可达性时距圈覆盖状况。魏伟[3]等以石羊河流域为研究区,选取2000年、2006年、2010年三期遥感影像为数据源,采用成本加权距离和城乡聚落体系潜能指数对传统的场强模型进行改进,综合利用扩张强度指数、扩张速度指数等分析研究石羊河流域内部城乡聚落体系空间结构分异。吴茵[4]等以城镇空间相互作用理论为依据,采用平均距离摩擦指数和成本加权距离改进现有的空间相互作用理论模型、引力模型和场强模型,定量分析城镇间的空间联系和组合特征,进而明晰区域城镇体系的空间结构。本文主要通过ArcGIS中空间分析模块的距离分析函数工具,根据研究区DEM数据,规划出一条成本低、距离短、不受河流阻碍的公路。需要强调的是本文所研究的最短路径是基于栅格数据,与网络分析工具模块中的路径分析、邻域分析工具模块中的近邻分析不同。前者是基于网络结构,比如道路网络数据、自来水管道网络等,求取设施点和事件点之间的网络距离,这个距离可以是时间最短,也可以是距离最短,但必须从已存在路线中挑选。近邻分析首先求取的是欧氏直线距离,其次出发点和到达点都是要素数据,不适合本文所采用的栅格数据。
1.最短路径相关概念
1.1 源
源是指距离分析中的目标或目的地,如医院、车站、水库、城市中心等。源的表现形式可以是离散的点要素、线要素或者面要素。要素之间允许邻接,但属性不可以一样。无论是栅格数据还是矢量数据都能表示源。
1.2 成本
成本可以理解为达成目标或者目的地的花费,包括自然障碍地物(山地、河流、湖泊等)和人文障碍地物(建筑物、铁路、高速公路等)的阻隔、时间、金钱、人们的主观感受、安全性等等[5]。影响成本的因素或多或少。例如,楼盘的开发建设、地皮价格、绿化率、容积率、交通区位、购物服务、娱乐配套、医疗资源等都不可忽视。成本栅格承载着从某个像元经过的代价,该图层的获取依赖于对影响因素的重新分类、分级、加权,故而将成本表示成如下:成本=影响因素1×权重1+影响因素2×权重2+…+影响因素N×权重N。
1.3 成本距离加权数据
成本距离加权数据还可以叫做成本累计数据,表示任一像元到距离最近、成本最低目的地最低累积成本。该方法结合客观实际,综合多方面影响因素,能够解决复杂地理问题。在空间分析中,广泛使用的是欧氏距离,在实际情况中,要从山的一边抵达另外一边,理论上最近的距离是直线贯穿,但隧道贯通的成本很高,此时还可以选择翻山或者绕路,后两者对于步行更有可行性。但翻山和绕路相比,假如以时间为成本,翻山耗时2.5小时,绕路耗时2小时,此时翻山的付出大过绕路的付出,选择绕路作为最小成本路径更合适。
1.4 距离方向数据
该数据代表着从任意像元开始,沿最少成本路径接近最近目标的前进方向。每个单元都有一个值,这个值是1、2、3、4、5、6、7、8中的一个,代表着不同的方向。在一个9×9的方格集合中,最中心的方格值为0,是目标点,当值为1时表示该方格在目标点的正东方,为2时表示在东南方,为3时表示在正南方。即从正东方开始顺时针方向旋转,每次旋转45°,值从1开始依次增加到8,每个格的方位随之改变。
1.5 距离分析函数
函数距离、直线距离的量化方式一共有11个,具体有廊道分析、成本分配、成本回溯链接、成本距离、成本路径、欧氏距离、欧氏方向、欧氏分配、路径距离、路径距离分配、路径距离回溯链接。
2.最短路径实现
2.1 数据准备
本文采用的实验数据包括某选址地区DEM数据、水系栅格图以及设定公路起点和公路终点的矢量点状数据。
2.2 数据处理
利用成本路径求取最短路径,用到的分析工具有地形因子计算、焦点统计、重分类、栅格计算器,最重要的是距离分析模块中的各个工具。由于山地的坡度、河流的分布与出行时长、出行距离、建设成本直接相关,需要利用DEM数据生成坡度地形因子并结合水系栅格图创建成本数据集。
2.2.1 因子提取
坡度既是微观地形因子,也是一阶地形因子,提取非常简单,通过【工具箱】→【系统工具箱】→【空间分析工具箱】→【面分析】→【坡度】,输入DEM栅格数据集,得到该DEM的坡度因子。
2.2.2 重分类
重分类是重新划分栅格数据的像元值范围,分配给单个值或值范围新值。选择【空间分析工具箱】→【重分类】,输入数据为河流栅格,分类方法选择等间距,分为4级,分类过程(如图1所示):
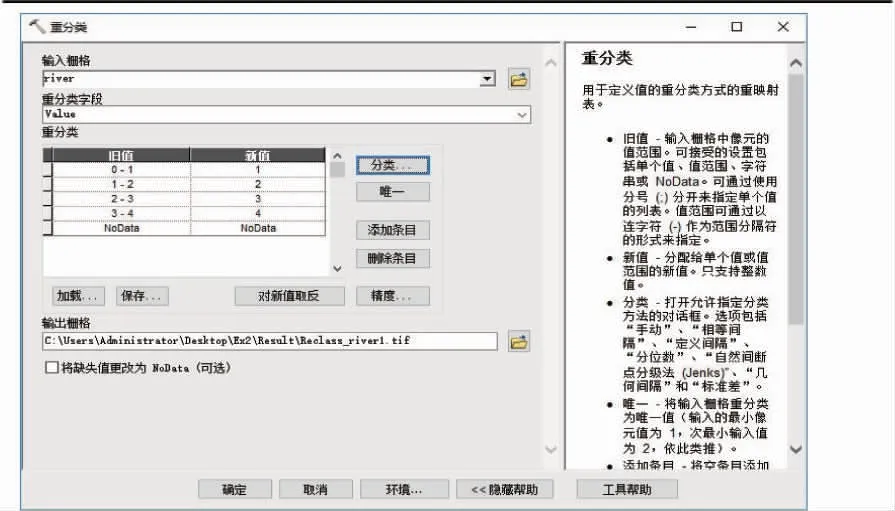
图1 河区图重分类设置
同样的流程和方法对坡度图进行重分类,等间距分为10级,坡度高低分级值大小成正比,结果中颜色越浅的地方,地势越平坦,颜色越深的地方,地势越高陡,分类结果(如图2所示):

图2 坡度重分类结果
2.2.3 邻域统计
地形起伏度是在指定范围内,最高点海拔高度减去最低点海拔高度的结果,通过焦点统计、栅格计算器实现。选择【空间分析工具箱】→【邻域分析】→【焦点统计】,输入栅格为DEM数据,统计类型分别选择“MAXIMUM”、“MINIMUM”,求得研究点固定邻域范围内的最大值、最小值。选择【空间分析工具箱】→【地图代数】→【栅格计算器】,地形起伏度=MAXIMUMMINIMUM。对得到结果进行重分类,方法选择等间距,一共分为10级,起伏度的大小与分级数成正比,分级结果(如图3所示):从图中可以看出研究区西北部分高低落差比较大,可能不适合修建公路。

图3 起伏度重分类
2.2.4 成本加权
通过【空间分析工具箱】→【地图代数】→【栅格计算器】,利用重分类后的河流栅格、坡度、地形起伏度进行成本数据集计算。计算公式为:成本加权数据=重分类坡度数据×0.6 +重分类起伏数据×0.4+重分类河流数据,意味着每个栅格的成本组成为0.6的坡度值、0.4的地形起伏度和全部的河流重分类值,三者的影响程度以河流因子为首,坡度因子和地形起伏度因子次之,计算过程(如图4所示):

图4 栅格计算器参数设置
通过【空间分析工具箱】→【距离】→【成本回溯链接】,参数选择中,【输入栅格数据或要素源教据】为原始DEM数据,【输入成本栅格数据】为上述计算得到的成本加权数据,输出得到回溯链接栅格数据,是最小成本源的最小累积成本路径上的下一个相邻像元。
通过【空间分析工具箱】→【距离】→【成本距离】,参数选择中,【输入栅格数据或要素源教据】为原始DEM数据,【输入成本栅格数据】为上述计算得到的成本加权数据,输出得到距离栅格数据,是每个像元从成本面或到成本面上最小成本源的最小累积成本距离。
由此就得到了道路选线的方向栅格和距离栅格。
2.2.5 最短路径的实现
选择【空间分析工具箱】→【距离】→【成本路径】,参数选择中,【输入栅格数据或要素目标数据】选择原始DEM数据,【成本距离栅格数据】选择距离栅格数据,【输入成本回溯链接栅格数据】中选择方向栅格数据,单击【路径类型】下拉箭头,选择计算模式“Each Zone”,得到结果(如图5所示):
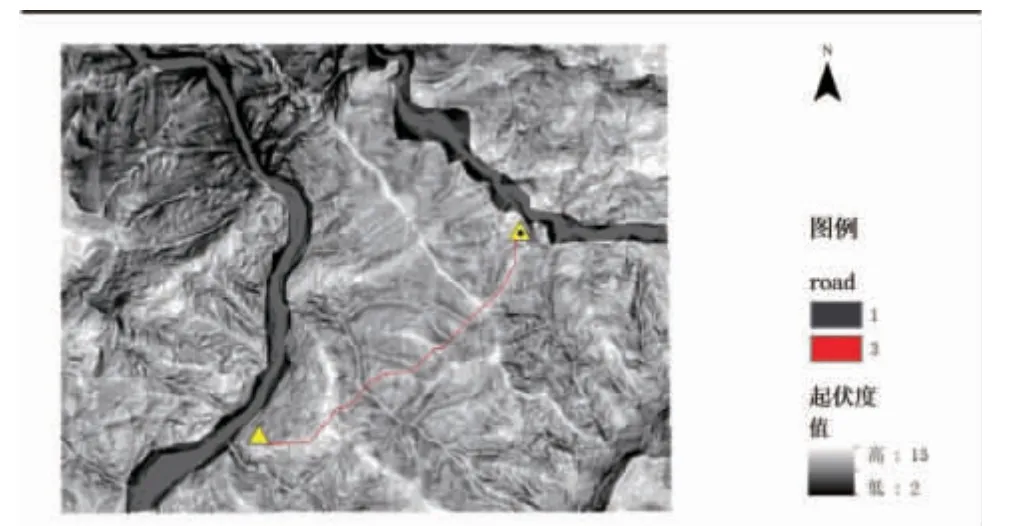
图5 最短路径图
图5中的红色线段就是最小成本路径,从起始地点到目的地既考虑距离,又考虑其他付出代价的最佳路线,可为新公路的规划提供决策参考。明显可以观察到这条路径并不满足传统的“两点之间直线最短”,而且避开了河流,在地势较为平坦的东南区域。这是因为考虑多重因素综合作用,在求取最小成本距离时不能只考虑距离,还要顾及地形的坡度和起伏度对于行进方向和行进距离的影响,比如盘山公路的设计,虽然,道路距离不是最短的,但是爬升效果却是最佳的,如果有河流存在,不管是跨越河流还是绕过河流,都会增加设计开发建设的成本。
3.结束语
成本距离分析应用众多,实用价值极高,比如景区各个景点之间的可达性设计、交通工具配置;滑坡泥石流发生时,道路塌陷的情况下,抢险救灾路线的规划;水库和自来水厂之间的最小成本连接方式等。总的来说,在出发点、目标点都确定的情况下,路线的规划与选取方式多种多样,距离分析为不同条件下最佳路径的选取提供理论依据、技术支持和科学决策。在有现成网络数据的情况下,可以通过网络分析来判断;如果有矢量数据,只需要计算直线距离,通过近邻分析实现。但是判断路径是否优良,影响选线的因素也不是单一存在,互相独立的,比如时间和金钱不能兼得,选择航线,速度快但是价格昂贵,选择铁运耗时长但是成本低廉。这些影响因素可能互相矛盾,也可能相互制约,各方面的作用力在不同情况下重要程度也会发生变化,即权重改变,需要根据实际情况选取成本种类、成本分级等。设置符合最佳需求的权重,计算合适的方向和距离,才能得到最小成本路径。根据本文研究区实际地形地势,实验过程中主要考虑到的是地表倾斜程度、相对地势和河流分布对路径成本的影响。但是如果变换了研究区,影响因素的选取和权重的设置都需要因地制宜,比如考虑已建成设施点、交通工具等。本文利用地理信息系统中空间分析功能来求取栅格数据中两点之间的最小成本路径,可作为道路选取、资源调配辅助分析的一种方法,但此法仅是通常理论基础下的解决方案,仅是给这一问题的解决提供一个参考。

