基于DIC的铝合金薄壁缺口件多轴疲劳行为
陈亚军,徐鹏达,王付胜,刘辰辰
(中国民航大学 中欧航空工程师学院,天津 300300)
7075铝合金凭借其良好的综合性能[1],经常作为高强度结构件材料,被广泛应用于飞行器的制造过程中,如飞机蒙皮、翼梁等部件[2-3]。飞机的运行工况复杂,其零部件即便在宏观上只受简单载荷作用,在零件的连接处也会受到复杂的多轴载荷。因此,对于缺口件试样进行多轴疲劳失效分析十分重要。王英玉等[4]对航空铝合金LY12CZ缺口件进行比例和非比例多轴疲劳实验,发现缺口处裂纹方向与最大剪应力幅及最大剪应变幅的方向相符合。Fatemi等[5]对铝合金7075-T6和2024-T3薄壁圆孔管状试样进行了多轴疲劳实验,发现相较拉应力,扭应力对于加快裂纹扩展更有效果,且缺口试样的宏观裂纹沿最大名义主应力平面扩展。王效贵等[6]对某钢材带缺口试样进行多轴疲劳载荷下的实验,发现应力和应变分量均在试样裂纹萌生过程中发挥作用。Berto等[7]对钛合金光滑件和缺口件进行了单轴和多轴疲劳实验,发现试样缺口尺寸不同,其轴向、扭向力学行为有较大差距。多轴疲劳加载条件下的寿命预测相对于单轴疲劳而言显得更为复杂[8-11],其中,缺口附近的应力/应变状态以及不同加载参数对材料力学行为和失效行为有着显著的影响,将二者引入疲劳寿命预测模型,从而准确预测多轴疲劳寿命是目前的一个研究热点。Gates等[12]对2024-T3铝合金缺口管状试样进行了多轴载荷条件下的多轴疲劳实验,使用Neuber模型和几种不同的临界距离法进行寿命预测,发现临界距离法预测结果具有更好的数据相关性。刘恩涛等[13]对7075-T7451铝合金实心棒缺口试件进行了多轴比例、非比例、随机应变疲劳实验,并应用有限元分析对比计算了缺口试件疲劳裂纹萌生寿命。陈震[14]应用名义应力法、Manson-Coffin公式、应力场强法和临界距离法来预测2A12铝合金缺口件多轴疲劳寿命,考虑应力梯度和尺寸因素的影响后,修正了Manson-Coffin方程。金丹等[15-16]对铁素体钢缺口件进行了一系列非比例载荷低周疲劳实验,并结合有限元分析得到的缺口根部的应力应变结果,应用SWT模型和KBM模型进行了疲劳寿命预测。
数字图像相关技术[17](digital image correlation, DIC),可以在疲劳实验的全过程表征材料表面的应变场,突破常见疲劳实验数据获取方法的局限性,为研究疲劳机理提供新的研究方法[18-19]。
结合DIC技术,本工作对7075-T651铝合金薄壁缺口件进行等效应力变量的多轴疲劳实验,分析缺口局部应变和多轴疲劳行为,对SWT模型进行修正,完成不同加载条件下的薄壁缺口件多轴疲劳寿命预测。
1 实验材料与方法
1.1 实验材料
实验所用为7075-T651铝合金,常温下的基本力学性能为:屈服强度492.95 MPa,抗拉强度538.90 MPa,弹性模量70.36 GPa。根据ASTM E2207测试标准,加工尺寸如图1所示的薄壁管状试样,圆孔缺口直径为2 mm。
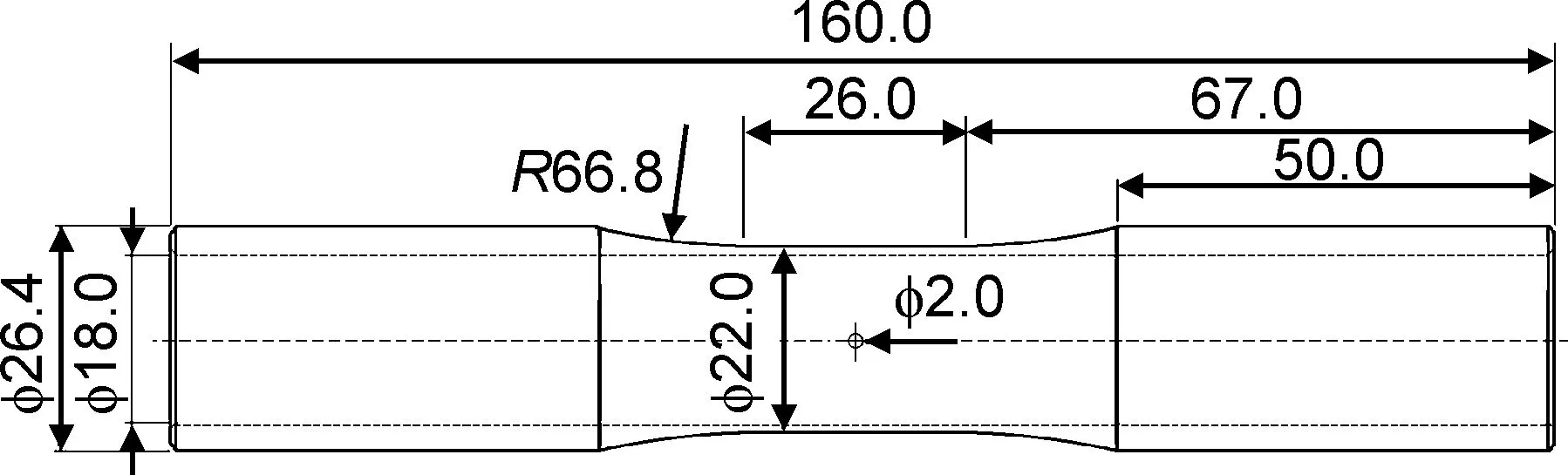
图1 薄壁缺口件试样尺寸示意图
1.2 实验方法
利用SDN100/1000电液伺服拉扭复合疲劳试验机,进行拉扭复合比例多轴疲劳实验,利用应力控制实验,采用von Mises等效应力准则计算确定轴向和扭向的应力,表达式为:
(1)
式中:σeq为von Mises等效应力;σ为拉应力;τ为扭应力。实验采用正弦波形加载,频率为5 Hz,表达式为:
σ=σasinωt
(2)
τ=τasinωt
(3)


表1 多轴疲劳实验加载参数
本工作采用非接触全场应变测量系统(VIC-3D),对多轴疲劳实验全过程进行表征。设计了配合VIC-3D系统拍摄的载荷谱,即在每100周次正弦波加载后,使疲劳试验机在拉向和扭向均保持2 s幅值载荷加载,并在此时进行实时应变拍摄,并如此循环直至失效。
2 结果与分析
2.1 多轴疲劳寿命实验结果
各参数实验结果见表2。可知,随着等效应力幅值的减少,所用缺口件多轴疲劳寿命呈现上升趋势。实验加载等效应力幅值为250 MPa时,试样平均寿命为2900周次;加载等效应力幅值为125 MPa时,试样平均寿命为83200周次。
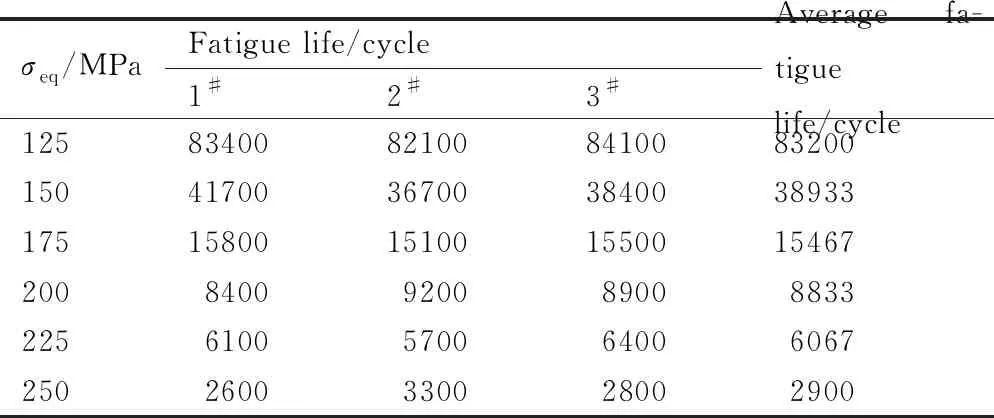
表2 缺口件多轴疲劳寿命实验结果
2.2 DIC应变分析
DIC分析中选取的x,y,z坐标系示于图2。可知,y轴即为试样宏观轴向,x轴即为试样宏观扭向,z轴即为试样横截面上的轴向垂直方向。在该坐标系下,轴向工程应变为εyy,扭向工程应变为εxx,剪切工程应变为εxy。

图2 DIC坐标系图
图3为工程应变与缺口件多轴疲劳寿命的关系曲线。加载不同等效应力幅值条件下,随着缺口件多轴疲劳加载周次的变化,DIC分析得到的缺口附近局部最大轴向工程应变εyy也随之改变,其变化趋势如图3(a)所示。由于加载较高的等效应力幅值可以得到较高的轴向应力分量,故εyy的初始值也会随着加载等效应力幅值的升高而增大。在不同等效应力幅值加载条件下都有以下规律,即εyy在疲劳加载前期变化很小,表明试样变形量不明显,试样处于裂纹萌生阶段;在疲劳实验的中后期,不同加载条件下的εyy均迅速增加,表明试样发生较大变形乃至断裂,其处于裂纹扩展和瞬断阶段。
相应地,随着缺口件多轴疲劳加载周次的变化,DIC分析得到的缺口附近局部最大剪切工程应变εxy也随之改变,其变化趋势如图3(b)所示。εxy的初始值同样随加载等效应力幅值的增大而升高。与轴向应变的变化趋势类似,在不同等效应力幅值加载条件下,都有以下规律:在裂纹萌生阶段,εxy在多轴疲劳加载过程的前期变化很小,即试样剪切变形量不明显;在裂纹扩展和瞬断阶段,不同加载条件下的εxy都迅速增加,试样剪切形变量迅速增加直至断裂。

图3 工程应变与缺口件多轴疲劳寿命的关系
图4为等效应力幅值为125 MPa的加载条件下,随着缺口件多轴疲劳加载周次的变化,试样缺口附近3个方向DIC应变云图,加载周次与疲劳寿命比值(n/Nf)分别为75%,90%,95%和99%。当n/Nf小于75%时,试样缺口附近轴向、扭向和剪切工程应变均变化不大,处于疲劳加载的前期;当n/Nf达到90%时,在试样缺口附近观察到显著的应变集中现象;而随着疲劳加载周次的增加,该现象逐渐增强,并形成微裂纹,微裂纹逐渐扩展,最终导致试样断裂。

图4 125 MPa等效应力幅下工程应变随缺口件多轴疲劳寿命的变化
图5为等效应力幅值为225 MPa的加载条件下,随着缺口件多轴疲劳加载周次的变化,试样缺口附近3个方向DIC工程应变云图,n/Nf分别为75%,90%和99%。与加载等效应力幅值为125 MPa的试样相比,当n/Nf为75%时,加载等效应力幅值为225 MPa的试样缺口附近已经出现应变集中现象,使其在疲劳实验中更早出现微裂纹,故多轴疲劳寿命下降。

图5 225 MPa等效应力幅下工程应变随缺口件多轴疲劳寿命的变化
2.3 微观形貌分析
加载等效应力幅值为175 MPa的试样应变云图和断口微观形貌示于图6。在比例加载多轴疲劳实验中,试样断口一般呈现出裂纹源区、裂纹扩展区和瞬断区3种形貌。图6(a)为试样应变云图,由2.2节分析可知,疲劳实验中,应变集中首先出现在缺口根部,从而导致微裂纹的萌生。由图6(b)可以看到,裂纹源区呈放射状河流形貌。在裂纹扩展区(图6(c))观察到明显的疲劳条带。图6(d)为瞬断区形貌,观察到大量韧窝。

图6 175 MPa等效应力幅值下试样断口应变云图及微观形貌
不同等效应力幅值加载下试样断口裂纹扩展区的微观形貌示于图7。不同加载条件下,裂纹扩展区均可以观察到疲劳条带。同时,在较低等效应力幅下,疲劳条带较为密集,疲劳寿命也较高(图7(a));较高等效应力幅下,疲劳条带较为稀疏,对应疲劳寿命较低(图7(b))。

图7 不同等效应力幅值下裂纹扩展区的微观形貌 (a)125 MPa;(b)225 MPa
3 多轴疲劳寿命预测
3.1 模型回顾
基于缺口件疲劳行为和失效机理,同时采用DIC分析得到的应变数据,本工作应用应力集中系数法,最大剪应变法以及临界平面法进行缺口件多轴疲劳寿命预测。
应力集中系数法[14]中,对于多轴比例加载条件,疲劳应力损伤参量σcr的表达式为:
σcr=σeq×Kf,eq
(4)
式中:Kf,eq为等效疲劳缺口系数,可由有限元计算得到[14],值为2.97。与Manson-Coffin-Basquin模型结合进行多轴疲劳寿命预测,其表达式为:
(5)
式中:E为弹性模量;σ′f为疲劳强度系数;b为疲劳强度指数;ε′f为疲劳延性系数;c为疲劳延性指数。最大剪应变法[20]认为,剪应变能够代表拉扭复合加载过程中的损伤,故可将最大剪应变视为损伤参量,表达式为:
(6)
式中:γmax为最大剪应变;ν是泊松比。
近年来,临界平面法被广泛运用于多轴疲劳领域。Socie[21]提出的SWT应变能密度法修正模型,可以用于比例和非比例多轴疲劳寿命预测,由临界平面上的最大主应力σn,max和主应变变程的一半Δε1/2组成疲劳损伤参量WS,其表达式为:
(7)
本工作所用7075-T651铝合金的疲劳力学材料常数如表3所示,其中σy为屈服强度,σu为极限强度。
3.2 修正SWT寿命预测模型

表3 7075-T651铝合金疲劳力学参数
(8)
图8为临界平面示意图。可知,临界平面可由试样水平截面旋转角度ψ得到,其中n向为临界平面正应力方向,l向为该正应力方向的垂直方向。

图8 临界平面示意图
通过引入坐标系转换矩阵,可以得到加载的应力矩阵[Σ]和临界平面上应力矩阵[Σ]cr之间的关系为:
(9)

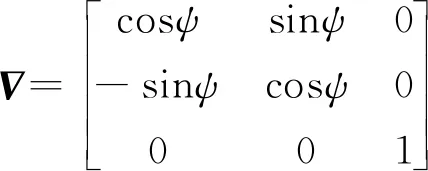
(10)
加载应力矩阵[Σ]和临界平面上应力矩阵[Σ]cr的表达式分别为:
(11)
(12)
式中:σl,a为l轴方向的正应力幅值;τnl,a和τln,a分别为临界平面剪切应力幅值,则σn,a与σa,τa之间的关系为:
(13)
类似地,可推导得到DIC分析得出的应变矩阵与εn,max之间的关系。通过引入DIC分析得到的工程应变,加载应力导致的应变矩阵[E]如式(14)所示:
(14)
式中:εa为试样坐标系下的轴向应变;εa,t和εt,a为试样坐标系下剪切应变γ的一半;εt为扭向应变。上述物理量与εyy,εxy和εxx分别对应。
临界平面上的应变矩阵[E]cr如式(15)所示:
(15)
式中:εn为临界平面上的正应变;εnl和εln为临界平面上的剪切应变;εl为垂直于临界面的正应变。对于不同的加载条件,选择同一阶段的应变场进行工程应变的取值实验,即DIC所得应变场中出现明显应力集中区域时,并选择应变场中各项的最大值,该值一般出现在缺口边缘区域。不同坐标系下的应变矩阵之间的关系为:
(16)
从而推导出临界平面上的最大正应变εn,max为:
εn,max=εa,maxcos2ψ-γmaxsinψcosψ+εt,maxsin2ψ=
εyy,maxcos2ψ-εxy,maxsinψcosψ+εxx,maxsin2ψ
(17)
式中下角max表示该量的幅值。
3.3 寿命预测结果及对比
应用应力集中系数法,最大剪应变法以及修正SWT模型进行寿命预测,对于不同等效应力幅值,寿命预测所需应力应变参数示于表4。

图9 不同等效应力幅值条件下的临界面 (a)125 MPa;(b)225 MPa

表4 寿命预测模型相关参数
应用3种模型进行寿命预测,结果如表5所示。可知,应力集中系数法的预测结果与实验平均寿命相差较大,该方法不适用于本实验条件(其中Kt为应力集中系数,Kf为疲劳缺口系数);最大剪应变法的预测结果与实验平均寿命相比过于保守,且预测精度随着等效应力幅的增加而降低,虽然其利用了DIC分析得到的最大剪应变,但仍然不能对本实验条件下的试样疲劳寿命进行较准确的估计;修正SWT模型利用DIC分析得到临界平面角度和缺口附近各方向最大工程应变,基于临界平面上最大正应力和最大正应变,推导得到了适用于缺口件多轴疲劳寿命预测的公式,预测结果与实验平均寿命比较接近。

表5 寿命预测结果
本工作提出的修正SWT模型预测寿命与实验寿命的对比示于图10。可知,修正的SWT模型寿命预测结果全部位于2倍分散带之内,表现出良好的预测能力。
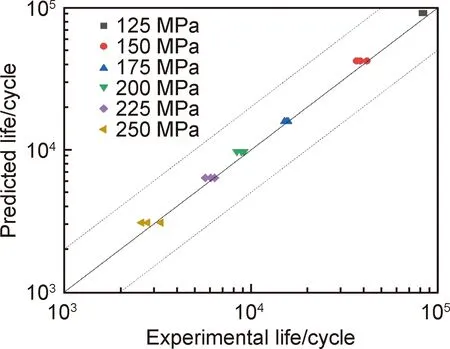
图10 修正SWT模型寿命预测结果
4 结论
(1)随着等效应力幅值的增加,材料多轴疲劳寿命随之下降。等效应力幅值从125 MPa增加到250 MPa时,试样平均寿命从83200周次下降至2900周次。
(2)不同加载条件下,DIC分析得到的轴向工程应变εyy,扭向工程应变εxx和剪切工程应变εxy在裂纹萌生阶段基本没有改变,在裂纹扩展和瞬断阶段发生显著变化,3个应变量的值均随加载等效应力幅值的增大而上升。应变集中现象随疲劳周次的增加而逐渐增强,形成微裂纹,并逐渐扩展直至试样断裂。
(3)结合DIC分析得到临界平面角度和缺口附近各方向最大工程应变,基于临界平面上最大正应力和最大正应变,得到适用于应力控制实验的修正SWT模型。本工作提出的修正模型预测结果全部位于2倍分散带之内,表现出良好的预测能力。

