裂隙岩体非稳定渗流场与应力场耦合分析研究

潘广良

(方正县河湖运行保障中心，黑龙江 方正 150800)

1 绪 论

深厚覆盖层地质条件复杂，渗透性大，对大坝的安全稳定运行造成一定影响，在设计阶段需着重考虑防渗体系的构建。当大坝完建蓄水时，坝体因自重和不断增加的水荷载，坝基覆盖层和大坝填筑料的渗透性出现变化，都将给大坝安全运行带来很多隐患。同时，岩体渗流很大程度上取决于裂隙结构面，几何参数改变岩体渗透性，所以正确合理地分析裂隙岩体的渗流场和应力场的分布就显得极其重要。

2 裂隙岩体等效连续介质渗透原理

裂隙岩体通常采用渗透张量体现渗透各向异性，二维等效连续介质渗透系数张量为[1]：

(1)

式中：bi、ci为第i组裂隙张开度和间距；μ为水的动力黏滞系数。

2.1 渗流场对应力场的影响

该影响作用通过水荷载逐步施加完成的，水压力包括渗透静水压力和渗透动水压力。渗透静水压力p表达式为：

p=γ(H-y)

(2)

(3)

式中：fx、fy为渗透动水压力分量。

2.2 应力场对渗流场的影响

该影响通过裂隙宽度改变达成岩体渗透系数的变化[2]，裂隙岩体受正、剪应力作用示意图，见图1。可得裂隙面上承受的正应力σn为：

σn=σ1cos2β+σ3sin2β

(4)

正应力作用后的裂隙隙宽变量△b表达式为：

(5)

式中：Kn0为初始法向刚度；b0为初始隙宽；bm为机械隙宽。

故裂隙最终隙宽为：

b=b0+△b

(5)

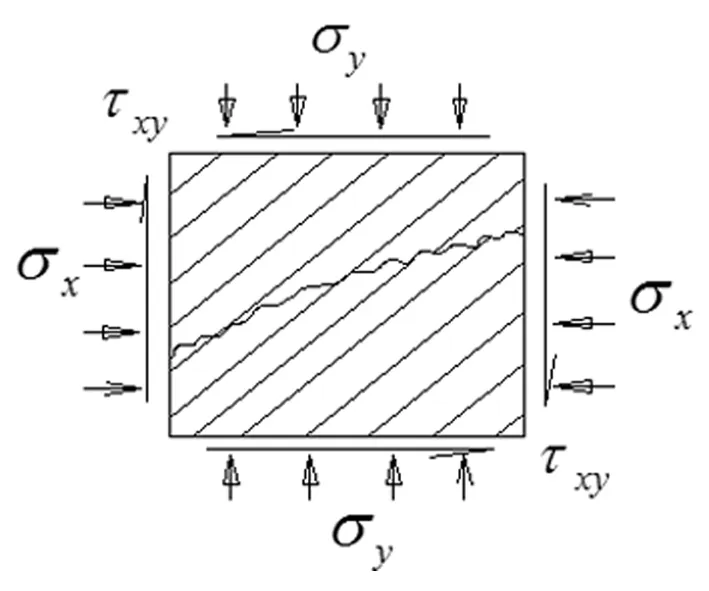
图1 裂隙岩体受正、剪应力作用示意图

3 工程算例

3.1 工程概况

某面板堆石坝坝高60.0m，上、下游水位分别为55m和5m。通过实测渗流资料得知绕坝渗流较小，故不考虑坝体渗流。计算时坝体主要荷载为上下游水荷载、渗透水压力荷载、坝体自重[3]。有限元模型边界定义：上游沿坝踵、下游沿坝趾各50m，覆盖层取80m。坝基岩体裂隙面包括竖直1组，水平1组，裂隙隙宽1.0mm，间距为1.0m，初始法向刚度Kn0=1.572×104MPa/m[4]，故可知渗流场初始渗透系数张量为：

(6)

坝体及基岩示意图，见图2；有限元网格剖分图，见图3。模型共剖分187个单元，116个结点。

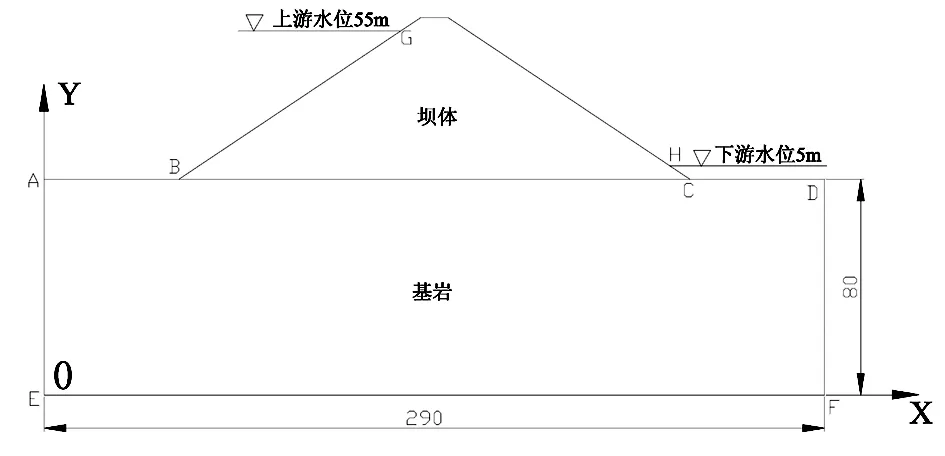
图2 坝体及基岩示意图

图3 有限元网格剖分图

坝体及基岩力学参数统计表，见表1。

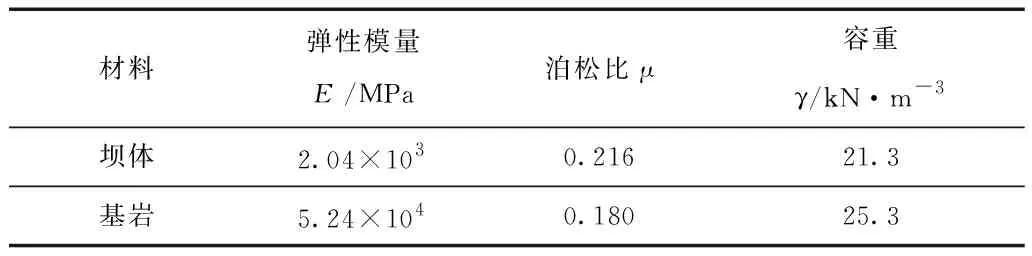
表1 坝体及基岩力学参数统计表

1)渗流场边界条件：水头边界：H|AB=55m；H|CD=5m；流量边界：QAE=QEF=QDF=0。

2)应力场边界条件：x向位移v|AE=v|DF=0；y向位移w|EF=0，贮存系数为Ss=6.8×10-5。

3.2 计算结果

当上游库水位以1m/d的速率下降，下游水位保持不变，此时坝体及坝基的渗流场与应力场耦合分布结果。初始时刻不计耦合的坝基水头等值线图，见图4；初始时刻考虑耦合的坝基水头等值线，见图5；不计耦合的坝基应力场σx等值线图，见图6；考虑耦合的坝基应力场σx等值线图，见图7；不计耦合应力场τxy等值线图，见图8；考虑耦合的应力场τxy等值线，见图9。

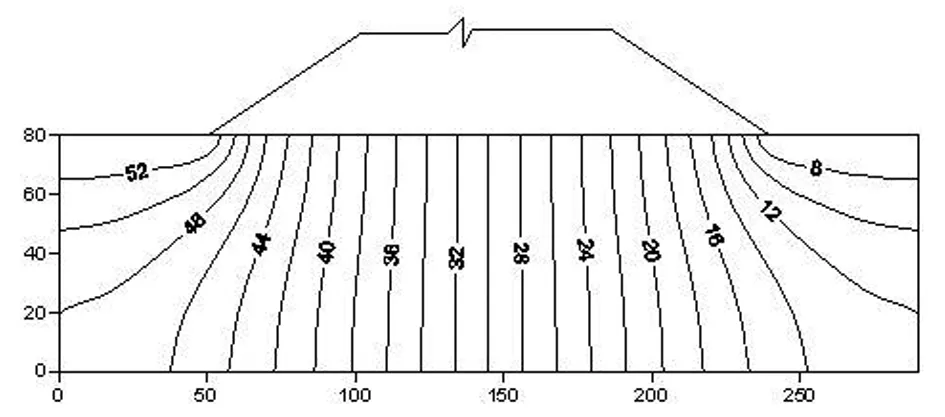
图4 初始时刻不计耦合的坝基水头等值线图

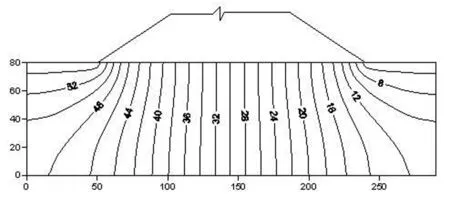
图5 初始时刻考虑耦合的坝基水头等值线

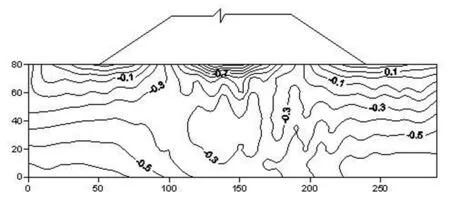
图6 不计耦合的坝基应力场σx等值线图

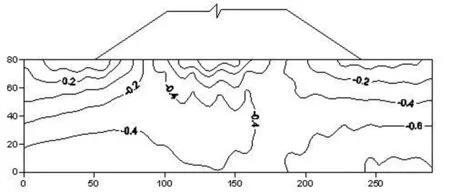
图7 考虑耦合的坝基应力场σx等值线图

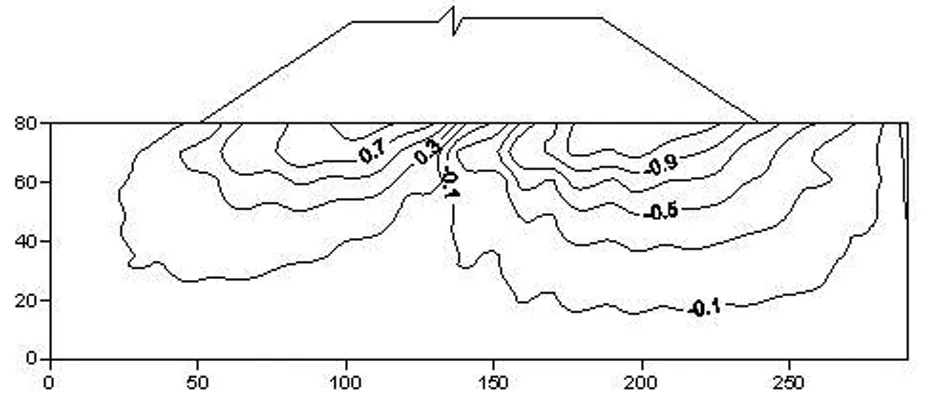
图8 不计耦合应力场τxy等值线图

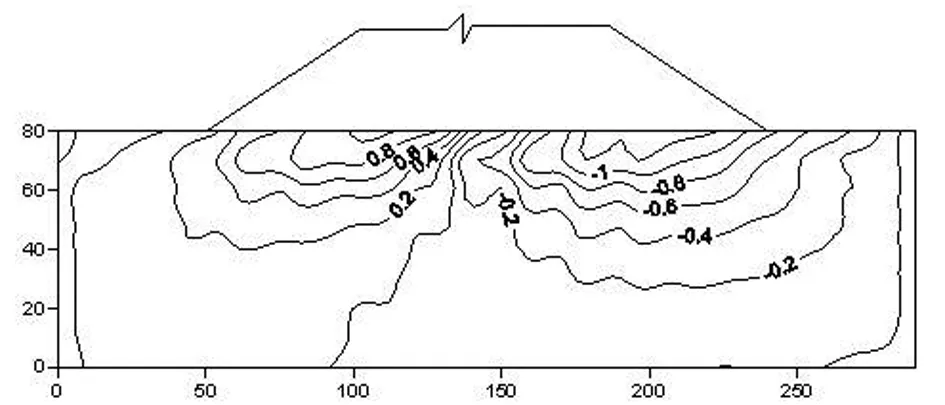
图9 考虑耦合的应力场τxy等值线图

1)渗流场计算结果分析：从初始时刻的计算结果来看，考虑耦合与否的渗流场结果相差较大。当考虑两场耦合时，坝基岩体裂隙不断相互挤压，造成裂隙宽度变小，此时渗流量降低。同时因渗透压力增大，裂隙宽度变小量上游大于下游，在坝基岩体中会出现水头滞后效应，水位下降时间越久，滞后效应越显著。

2)应力场结算结果分析：从应力场计算结果来看，考虑耦合与否的应力场各分量变化趋势基本相似，分析是受渗透静、动水压力影响，各应力分量σx、σy、τxy均不同程度增加，大坝及坝基稳定更加贴合实际，故考虑岩体裂隙渗流场和应力场的耦合作用是非常有必要的。

4 结 论

文章在裂隙岩体二维渗流场与应力场作用机理的理论基础上，结合工程建立二维有限元模型，分析非稳定渗流场作用下的应力场变化，应力场带来的坝基水头变化，比较耦合与否的计算结果，认为在本身稳定的坝基当边界条件变化时，仍有可能还不稳定，造成坝基失稳，所以在实际工程中要考虑渗流和应力的耦合作用。