基于不等波长模型的II型轨道板上拱稳定性公式

杨俊斌，张光明，杨荣山，刘学毅

（西南交通大学高速铁路线路工程教育部重点实验室，四川成都，610031）

近年来，每逢夏季高温天气，II型无砟轨道结构总会出现轨道板上拱伤损。轨道板上拱的表现形式均为上拱处两侧轨道板向中间破损处的位移，严重时，上拱区域两侧一定长度范围内的扣件与钢轨也发生相对位移，越靠近破损的板间接缝处，位移越大。根据上述上拱伤损的发生时间和表现形式，结合II型轨道板的纵连结构特征，即可知轨道板的上拱伤损为板体内温度压力所致。当温度压力足够大时，轨道板最终会在上拱方向产生明显的结构变形或破坏。轨道板的上拱伤损对线路结构的整体性及平顺性均会造成较大破坏，而且出现频率高，无法事先预测，因此，上拱伤损会严重威胁高速列车行车安全。

目前，国外的纵连无砟轨道未出现轨道板上拱，因此，并未对轨道板上拱进行过相关研究。国内针对轨道板上拱的研究集中于上拱对轨道结构层受力及形变的影响[1-10]以及上拱形成机理[11-16]这2方面。前者主要集中于其对高速列车的行车安全性的影响。后者的研究中，由于轨道板在上拱方向产生明显的结构变形或破坏时即可认为轨道板丧失稳定，因此，曾毅等[15-16]认为轨道板上拱现象的理论研究属于结构稳定性研究范畴，并基于能量准则采用“等波长模型”推导了轨道板上拱稳定性公式，而且采用该公式初步分析了轨道板的上拱稳定性，但是上拱稳定性解析研究方法中仍然存在2个问题需解决：1）在推导轨道板上拱稳定性公式时，采用等波长模型，即假定轨道板上拱变形波长两端铰支，但由于轨道板横截面具有较大的抗弯刚度，而且轨道板的上拱矢度为较小的竖向位移，上拱边缘的实际边界条件是介于铰支与固结这2 种状态之间，更接近于固结的状态，因此，采用该模型推导的轨道板上拱稳定性公式的计算结果可能会存在较大误差；2）除了轨道结构所用材料的物理力学影响因素外，轨道板上拱临界力还受变形波长、弹性初始弯曲、塑性初始弯曲、允许变形矢度这4个参数的影响，目前对这些关键参数的合理取值的研究较少。由无缝线路稳定性的相关研究可知，采用能量准则研究结构稳定性时存在“等波长模型”及“不等波长模型”这2种模型[17-18]。“等波长模型”假设初始波长与变形后波长相等，该假设等同于将变形波长两端视为铰支，而“不等波长模型”假设初始波长与变形后波长不相等，变形后波长小于初始波长。采用“等波长模型”对轨道板上拱稳定性研究时，存在上拱变形波长两端铰支的假定条件与上拱边缘实际边界条件不符合的问题。为此，本文基于能量准则，采用“不等波长模型”研究II型轨道板上拱稳定性公式及公式中的关键参数的合理取值这2个问题。

1 II型轨道板上拱稳定性理论

1.1 基本假设

1）轨道板纵向连接后，长度可以百千米计，轨道板横截面的高度与宽度相对于结构长度而言非常小，因此，在温度和压力作用下，轨道板可视为置于连续支承上的细长压杆。

2）轨道板上“V”型假缝仅为轨道板细部结构，忽略假缝对板体抗弯刚度的影响，将轨道板视为等厚板。

3）砂浆层与轨道板间的黏结状态在线路运营后将极大减弱甚至消失，在公式推导中不考虑砂浆层黏结强度。

4）钢轨及扣件系统的截面惯性矩相对于轨道板的截面惯性矩要小的多，忽略其在轨道板上拱中的抗弯能力。

1.2 变形曲线的线型确定

采用不等波长模型推导轨道板上拱稳定性公式时运用势能驻值原理。势能驻值原理中形变能是由变形曲线的二次泛函表示。轨道板上拱稳定性研究中形变能主要由板体上拱变形及作为板体上拱变形诱因的轨道板初始弯曲共同产生，因此，必须分别确定出轨道板上拱变形及其初始弯曲的线形。

轨道板上拱变形及其初始弯曲的真正变形曲线无法用初等函数或其有限项的组合来表达，通常近似变形曲线用的函数项数越多，其解的精确度越高，但变形曲线的选取不但涉及精度问题，而且影响计算的繁简程度，一般用三角函数较为方便。本文采用三角函数分别确定轨道板上拱变形及其初始弯曲的线型。

轨道板在温度压力作用下的竖向变形方向受板下结构层的限制，只能产生如图1所示的上拱变形。由图1可知：上拱区域的变形总体特征为中间高，两边低，即变形曲线的曲率是由两端向中间逐渐增加，该变形特征与无缝线路稳定性问题中钢轨变形特征相似。

由于无缝线路直线和曲线轨道的钢轨变形曲线均非常接近正弦曲线，同时正弦曲线计算比较简单，故无缝线路稳定性分析中将正弦曲线作为钢轨变形曲线。按照变形曲线线形既要表现出结构实际的主要变形特征（满足挠度、转角以及弯矩条件），又要满足线形连续及简便易用（变形曲线的表达式必须便于积分运算）的原则，轨道板的上拱变形曲线也采用半波正弦曲线表示。当上拱变形矢度为f，变形后波长为l，变形曲线y1可写为

轨道板的初始弯曲由弹性及塑性2 个部分构成。轨道板的弹性初始弯曲、塑性初始弯曲与板体上拱变形方向一致，参考文献[17]，本文将弹性初始弯曲和塑性初始弯曲均采用正弦平方曲线表示。当初始波长为l0，弹性初始弯曲矢度和塑性初始弯曲矢度分别为foe及fop时，对应于图2所示不等波长模型中初始弯曲及变形波长间的关系示意图，轨道板弹性初始弯曲yoe和塑性初始弯曲yop可分别写为

此时，考虑弹性初始弯曲变形和塑性初始弯曲变形时，轨道板在无温度压力作用时的变形曲线ys和有温度压力作用下的变形曲线yk可分别写为

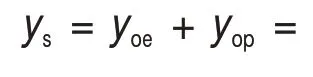
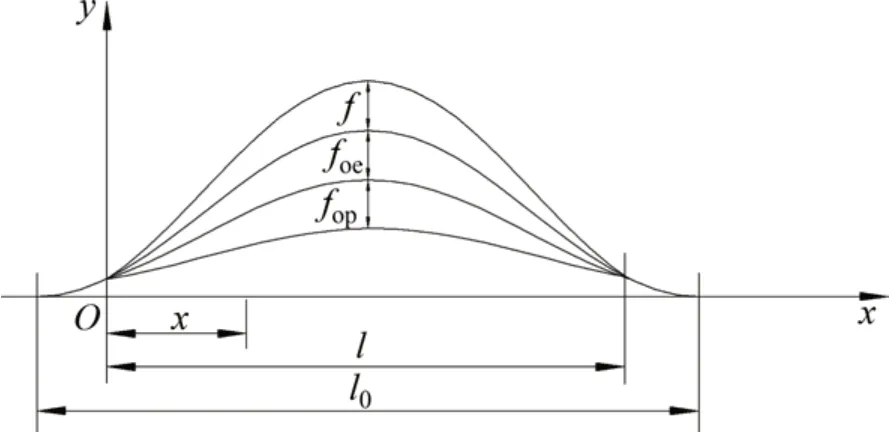
图2 初始弯曲及变形波长关系示意图Fig.2 Schematic diagram of relationship between initial bending and deformation wavelength

图1 II型轨道板上拱伤损形成示意图Fig.1 Schematic representation of the upper arch formation on the II type track slab

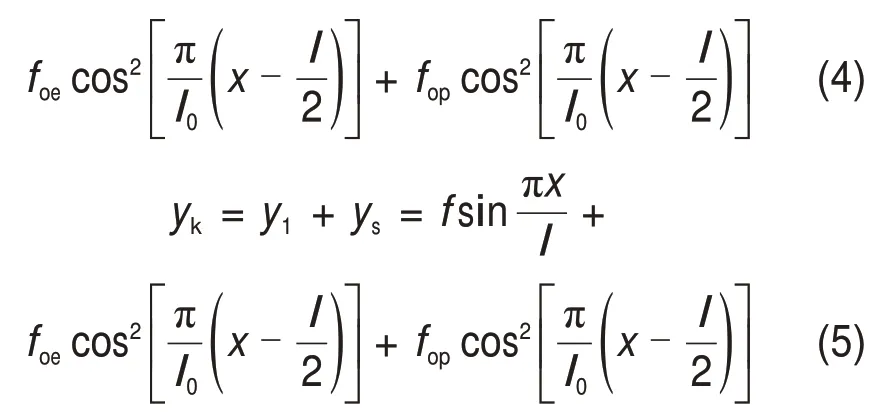
1.3 轨道结构形变能

在1.1节假设条件下，不考虑外力做功，在温度压力作用下，轨道板保持上拱稳定性的总能量由轨道板压缩形变能、弯曲形变能和重力势能这3个部分构成。

1.3.1 轨道板压缩形变能

温度压力作用下，轨道板由于压缩变形而产生压缩形变能。当温度压力为P，初始状态与变形后的单位弧长差为dlΔ，轨道板单位压缩形变能dA1可写为

轨道板上拱变形前后的单位弧长差dlΔ可由计算轨道板上拱变形后的单位弧长dlk与轨道板初始状态的单位弧长dls的差值获得。若设变形波长l中任一微小弧长dx 对应的变形前后的弧长分别为dls与dlk，则dls和dlk与轨道板上拱变形前后的曲线ys与yk的相互关系如图3所示。

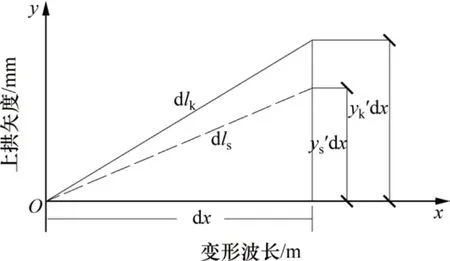
图3 弧长差示意图Fig.3 Schematic diagram of arc length difference

根据图3中所示各参数的相互关系，再结合二项式定理，可将dls，dlk与dlΔ分别写为

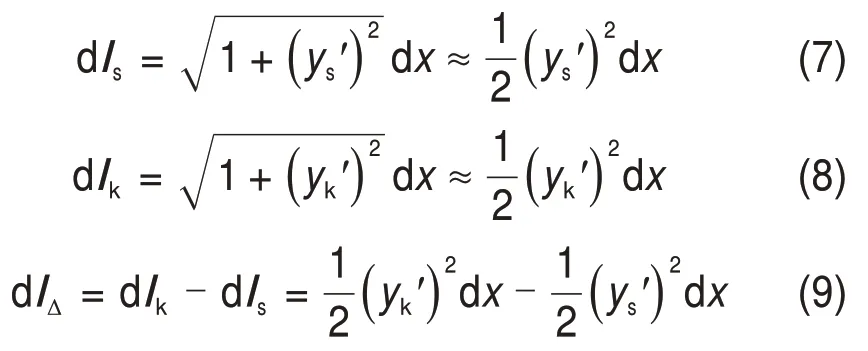
将式（4）、（5）及（9）代入式（6），并对式（6）求其关于变形波长全长范围的积分，则轨道板的压缩形变能A1可写为

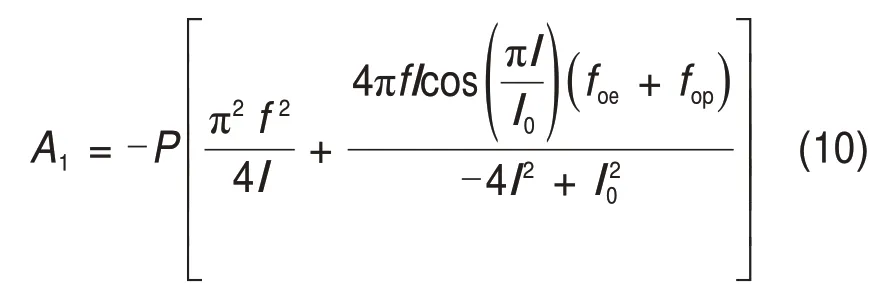
1.3.2 轨道板弯曲形变能

当轨道板在温度压力作用下产生上拱变形时，轨道板弯曲形变能包括由轨道板上拱变形的弯矩和由弹性初始弯曲的弯矩这2个部分共同产生的形变能。

若轨道板弹性模量为E，横截面惯性矩为I，截面转角为θ，轨道板上拱形成的弯矩为M，轨道板弹性初始弯曲的弯矩为Moe，由材料力学弯曲理论可知：dθ = y1″dx，M = EIy1″，Moe=EIyoe"。由这2个部分共同产生的弯曲形变能A2可写为

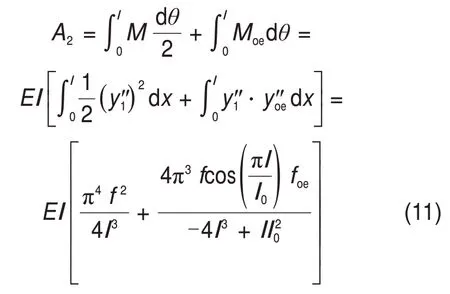
1.3.3 轨道板重力势能

将轨道板重力简化为沿板长度方向的均布荷载，若轨道板密度为ρ，轨道板横截面积为A，重力加速度为g，则轨道板上拱变形时增加的重力势能A3可写为

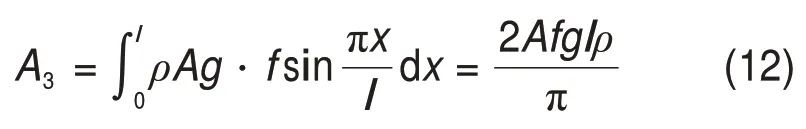
1.4 临界温度力计算公式

将式（10），（11）和（12）相加，即可得轨道板总势能A的表达式为

按照势能驻值原理，对式（13）求关于变形矢度f的偏导，即则轨道板上拱变形时的临界温度力P的表达式可写为

式（14）的意义是当初始弯曲（foe，fop，l0，l）一定，且在温度压力作用下轨道板产生变形时，若要使II 型轨道板上拱变形时保持结构稳定，则温度压力不应大于P。

2 关键参数取值

由式（14）可知，轨道板上拱临界力的影响因素众多，除去轨道结构所用材料的物理力学影响因素外，还受变形波长、允许变形矢度、弹性及塑性初始弯曲这4个参数的影响。因此，为保证推导的稳定性公式的正常使用，仍需确定上述4个参数的取值。

2.1 允许变形矢度

轨道板一旦上拱，上拱区域就会形成轨道结构的静态不平顺，这种静态不平顺会对轨道几何形位中的高低指标产生直接影响，高速铁路关于静态容许偏差管理值如表1所示[19]。运营期的高铁线路容许偏差以经常保养模式为准，轨道板由于上拱增加的幅度会导致线路的维修管理模式由经常保养升级为临时补修，甚至达到限速，由于线路的维修管理模式达到限速意味高速列车行车安全性已受到极大影响，因此，轨道板上拱后增加的幅度应以不致使线路维修管理模式升级为限速模式为原则，即轨道板上拱后增加的幅度应使线路维修管理模式保持在临时补修模式内。由表1可知：高铁线路维修管理模式由经常保养模式达到并保持在临时补修模式内时，允许最大增量为3 mm，所以，轨道板上拱允许矢度也不能超过3 mm，考虑到还会有其他因素造成高低的增加，本文建议将轨道板的允许上拱矢度定为2 mm。

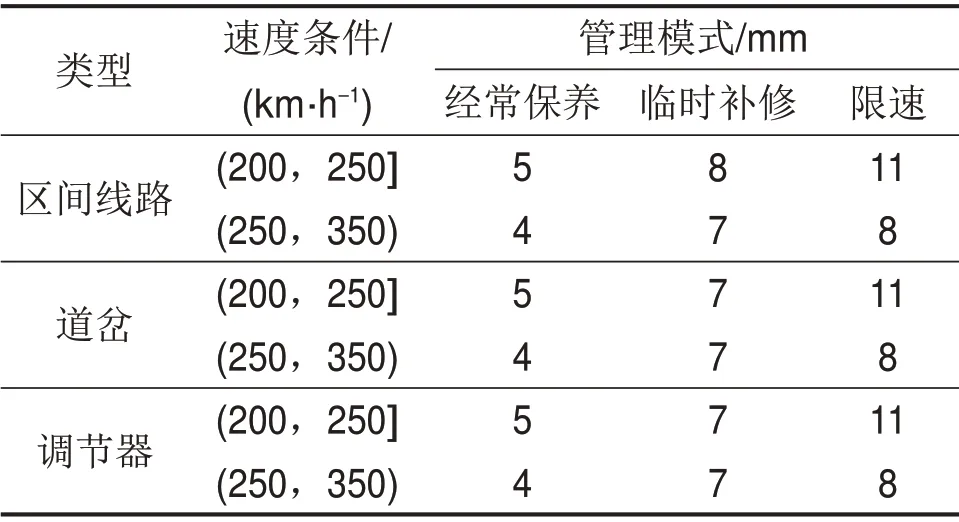
表1 高速铁路无砟轨道静态允许偏差管理值（高低）Table 1 Management values of static tolerance of ballastless track of high-speed railway（longitudinal level of track）

2.2 初始弯曲

轨道板的塑性初始弯曲在轨道板生产、铺设和使用中均有可能产生。

由于初始弯曲方向与轨道板上拱方向相同，轨道板上拱方向又与其厚度方向一致，因此，轨道板在生产中的塑性初始弯曲可参照轨道板的厚度误差来确定。轨道板外形尺寸偏差要求如表2所示[20]。轨道板厚度误差主要采用表2中的厚度及平整度2项指标进行控制，再通过表2中其余指标的辅助控制，轨道板在生产阶段的厚度误差为2 mm，因此，轨道板在生产中产生的塑性初始弯曲可能为2 mm。

表2 轨道板外形尺寸偏差的要求Table 2 Requirements for size deviation of track slab profile

按照现行施工技术标准，轨道板在安装就位时，各个结构层的施工误差最终累计到轨道板层时，误差为0.2 mm 以内[21]，因此，轨道板在铺设阶段产生的塑性初始弯曲在0.2 mm 以内，该值较小，本文对其忽略不计。

轨道板在使用阶段产生的塑性初始弯曲由使轨道板产生向上变形的各种因素造成，高速铁路中桥梁结构占比很大，桥梁多为预制箱梁简支结构，当梁端发生转角或者梁体产生徐变上拱时，纵连轨道板均有可能产生向上的弯曲变形。但实际上，梁端转角及梁体徐变上拱产生的向上变形主要会被轨道板下的底座板及CA（cement asphalt）砂浆层分别抵消，导致轨道板产生的向上变形会很小。梁端转角及梁体徐变上拱使轨道板可能产生的向上变形量均很小，因此，本文对轨道板在使用阶段产生的塑性初始弯曲忽略不计。

综上所述，本文以轨道板在生产过程中造成的厚度误差作为确定塑性初始弯曲的依据，由该依据确定的轨道板塑性初始弯曲为2 mm。

轨道板弹性初始弯曲的形成可认为与轨道板的离缝伤损密切相关。图4所示为轨道板弹性初始弯曲形成示意图。从图4可知，一段长度轨道板两端出现了板底与CA砂浆层间的离缝伤损，列车通过时，离缝区域轨道板要比非离缝区域轨道板的竖向下沉位移大，列车荷载长期作用下，离缝区域轨道板的变形会由弹性变形变为弹塑性变形，即一部分竖向下沉位移成为永久变形，轨道板在该位置形成向下弯曲，轨道板两端形成向下弯曲的同时，其中部会出现新的离缝区域，该离缝由轨道板向上变形产生，此时轨道板产生两端低、中间高的变形，该变形即成为了轨道板弹性初始弯曲。

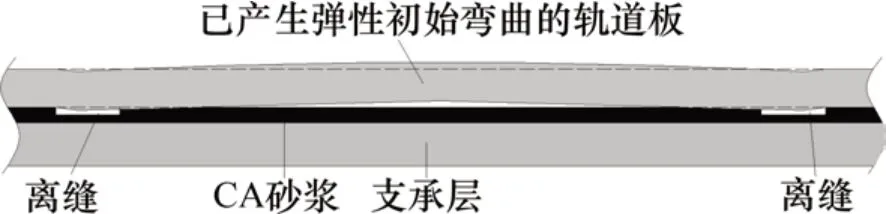
图4 轨道板弹性初始弯曲形成示意图Fig.4 Schematic diagram of elastic initial bending of track slab

目前，轨道板在离缝区域的塑性变形尚无成熟的研究成果可借鉴，由于轨道板的弹性初始弯曲与轨道板离缝伤损密切相关，因此，本文以文献[19]为参考，确定弹性初始弯曲取值。考虑到离缝是II型轨道结构的常见伤损，离缝伤损出现时还伴有CA砂浆材料的缺损及剥落等现象，达到III级伤损标准的离缝数量较多，因此，轨道板的弹性初始弯曲建议应以III 级离缝伤损中的离缝高度1.5 mm 为取值参考，为便于对该值的记忆及计算使用，同时考虑到1.5 mm 仅为III 级伤损最小值，本文将1.5 mm取整为2.0 mm，将2.0 mm作为II型轨道板的弹性初始弯曲。

2.3 最不利波长

由文献[16]可知，当允许变形矢度保持一定时，必然有一个变形波长能使临界力为最小。在不等波长模型中，使临界力为最小时的变形波长由初始波长和变形后波长共同组成，在该初始波长及变形后波长条件下，轨道板保持上拱稳定性的能力最弱，因此，初始波长及变形后波长这2个条件的组合即代表了采用式（14）对II型轨道板上拱稳定性进行研究时的最不利波长。

已有的上拱伤损统计资料表明，当轨道板上拱高度不超过7 mm 时，其上拱波长不大于10 m，不小于3 m。为确定最不利波长中初始波长及变形后波长的具体取值，同时为提高计算效率，以0.4 m 为级差，分别取初始波长l0由4.0 m 增加到19.2 m，变形后波长l 由3 m 增加到10 m，将这2个波长的不同组合作为计算工况，采用式（14）计算了各种工况下的轨道板的上拱临界力，计算中所需的其余参数的取值分别为：II 型轨道板宽度取2.55 m，厚度取0.20 m，弹性模量取3.5×1010Pa，密度取2 500 kg/m3，重力加速度取9.8 N/kg，允许变形矢度及弹塑性初始弯曲均取2 mm。

各种工况下计算的轨道板上拱临界力如图5所示。由图5 可知：各种工况下，最小临界力为21.66 MN，此时初始波长为6.7 m，变形后波长为6.1 m。因此，该初始波长及变形后波长即为使轨道板上拱临界力为最小的最不利波长。

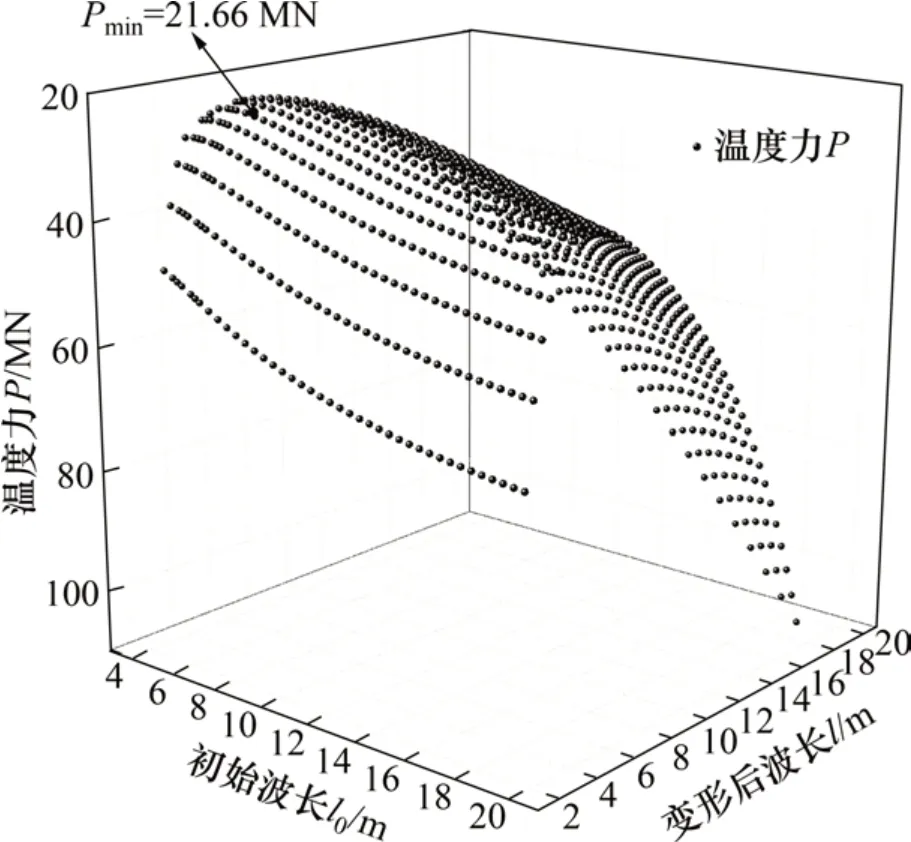
图5 轨道板上拱临界力图Fig.5 Diagram of critical force of upper arch on track slab

3 公式验证

为验证式（14），采用ANSYS 软件建立了轨道板上拱稳定性的三维数值计算模型。数值模型对稳定性公式进行验证的思路为：在初始弯曲（foe，fop，l0，l）相同的条件下，若施加在使数值模型的变形矢度为f时的温度压力等于同样变形矢度条件下的稳定性公式计算结果，则证明稳定性公式计算结果是正确的。数值模型中温度压力是由施加在轨道板单元上的升温幅度产生，当混凝土材料的线胀系数为α，弹性模量为E，横截面面积为A，轨道板的升温幅度ΔT 与临界温度力P 的关系式为[18]

由于数值模型中弹性初始弯曲和塑性初始弯曲需在建模阶段预先设定在模拟轨道板的实体单元上，而重力荷载只能在加载阶段施加，这与“轨道板的初始弯曲是在克服了重力作用后的变形”不符，因此，为使数值模型中的初始弯曲与实际情况一致，模拟轨道板的单元下部由非线性弹簧均布支承，非线性弹簧只产生压力不产生拉力，图6（a）所示为在最不利波长条件下，本文建立的轨道板上拱稳定性三维数值模型仅在重力作用时轨道板的竖向位移，由图6（a）可知：轨道板最大下沉位移仅为6.52×10-3mm，该值非常小，可以忽略不计，即说明建模阶段在轨道板上预设的弹性初始弯曲和塑性初始弯曲并没有在计算阶段由于重力的作用而减小，数值模型的初始计算条件与轨道板的实际受力情况是一致的。

在最不利波长条件下，先采用式（14）计算当容许矢度为2 mm，弹性初始弯曲、塑性初始弯曲以0.5 mm 为级差，均由1 mm 增加到3 mm 时的5 种工况下轨道板临界力，将计算的临界力代入式（15）求得这5种工况下轨道板允许升温幅度，然后，将允许升温幅度作为温度荷载施加在数值模型上即可求得5种工况下的轨道板上拱矢度。以工况3（弹性初始弯曲和塑性初始弯曲均为2 mm）为例，该工况条件下，数值模型计算的轨道板竖向位移云图如图6（b）所示。由图6（b）可知：轨道板上拱矢度为2.111 mm。

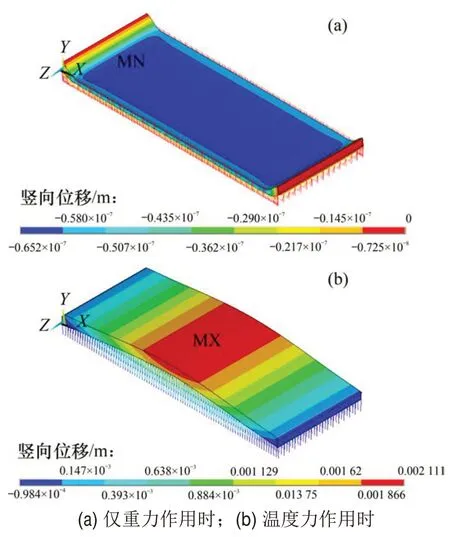
图6 轨道板竖向位移Fig.6 Vertical displacement of track slab

在上述5种工况下，式（14）中轨道板允许矢度取值与数值模型中求得的上拱矢度如表3所示。由表3可知：在5种工况下，稳定性公式中代入的上拱矢度与数值模型计算的上拱矢度最大相对误差约为9%，误差较小。因此，本文推导的II型轨道板上拱稳定性公式是正确的，适用于上拱稳定性计算。

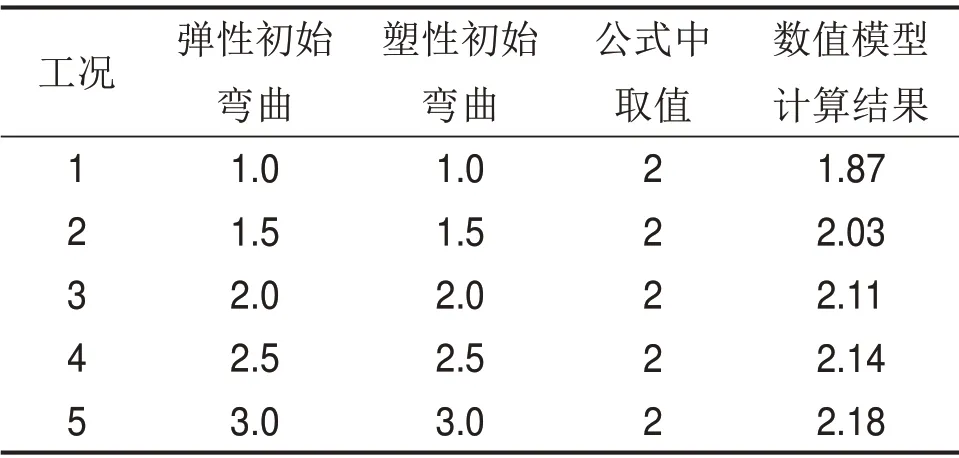
表3 公式中代入的与数值模型计算的上拱矢度对比Table 3 Comparison of the upper arch sagittal degree substituted in the formula with the numerical model calculationmm

4 2 种模型的稳定性公式计算结果比较

在研究轨道板上拱稳定性时，基于不等波长模型和等波长模型推导的稳定性公式均只用来计算轨道板上拱稳定性最弱时的临界力，因此，仅需对基于2种模型的稳定性公式计算的轨道板最小临界力进行比较，即可确定2个稳定性公式计算结果的差异。

本文确定的轨道板上拱允许矢度、弹塑性初始弯曲均为2 mm，将这3个参数代入文献[16]中的基于等波长模型推导的轨道板上拱稳定性相关公式，求得轨道板上拱时的最不利波长以及该波长条件下的最小临界力分别为6.07 m 和18.93 MN；在相同允许矢度及初始弯曲条件下，基于不等波长模型推导的稳定性公式计算的最小临界力为21.66 MN。因此，基于不等波长模型推导的轨道板上拱稳定性公式计算的临界力略大于等波长模型下的稳定性公式计算的临界力，两者相对误差约为15%。

5 结论

1）采用不等波长模型推导的上拱稳定性公式适用于II型轨道板上拱稳定性研究。

2）在采用本文推导的轨道板上拱稳定性公式进行相关研究时，建议将轨道板的允许变形矢度、弹性初始弯曲、塑性初始弯曲这3 个参数均取为2 mm。

3）当轨道板的初始变形波长取6.7 m，变形后波长取6.1 m时，轨道板保持上拱稳定性的能力最弱，建议将此初始波长及变形后波长的组合作为轨道板上拱稳定性研究时的最不利波长。

4）基于不等波长模型推导的临界力公式计算结果要比基于等波长模型推导的临界力公式计算结果大15%左右。