一种时空阵列电磁数据处理模型
周聪,汤井田,原源,兰学毅,郭冬
(1.东华理工大学核资源与环境国家重点实验室,江西南昌,330013;2.中南大学有色金属成矿预测与地质环境监测教育部重点实验室,长沙,410083;3.安徽省勘查技术院,安徽合肥,230041)
电磁勘探系统包括输入、输出以及地球介质等,输入端的场源条件、输出端的观测方式以及输入-输出间的相互关系等,是电磁勘探的基本研究内容,也是电磁勘探方法分类的重要依据。输入端有多种场源形式,主要包括天然电磁场、不可控人文场以及可控人工场等,它们各自具有不同的特征。天然电磁场的场源主要包括太阳风、雷暴等,它们通常距离遥远,场可近似视为以平面波形式垂直入射地球表面,具有很宽的频谱,并且在各个方向上的强度基本相当[1-2],但单频点的信号弱,信噪比低。由于人类电磁活动加剧,人文电磁场的影响日益严重[3-6],其以非平面波为主要成分,常导致基于平面波理论的常规数据处理结果出现畸变。特别地,在高频“死频带”(1~5 kHz)及低频“死频带”(1 Hz 附近)信号强度极低,阻抗更易受干扰影响[7]。为提高观测数据信噪比,人工场源被引入进行信号发送,以增强场源信号强度[8-9]。由于人工场源的引入,场源的影响随之出现,如产生非平面波效应、场源附加效应、场源阴影效应等[10-11]。为克服这些问题,研究者们提出了许多改进方案,主要包括增大发送功率以提高信噪比[12-13]、使用超大极距的固定发射台以扩大波区的测量范围[14-15]、采用编码电磁信号及相关检测技术提高数据的信噪比[16-18]以及采用张量发送和接收以扩大测量范围提高信噪比[19-20]等。总体而言,这些改进方案可有效提高数据观测质量,但难以同时利用天然场、人文场信息,也将导致采集成本增加。在输出端,测量仪器与观测手段的进步不断推动着电磁勘探技术的发展,主要观测方式逐步从一维、二维向三维过渡,对数据处理方法也不断提出新的要求。近年来,分布式测量及三维阵列勘探受到了人们广泛关注[21-24],有效提高了观测精度与空间分辨率,成为电磁观测的新趋势。然而,数据处理仍然只针对单个测站或部分场分量;天然场源电磁法数据处理一般针对单测站的张量电磁场进行,通过稳健估计提高处理质量,可控源电磁法数据处理常针对单测站的正交标量电磁场或单个电磁场分量[9-10]。多站数据的利用可以有效提高数据处理质量。远参考技术[25]最早实现了不同测站间数据的利用。通过引入参考道的观测数据,与测站的数据进行相关处理,以压制噪声,取得了很好的处理效果[2,26-30]。EGBERT等[31-33]提出了针对大地电磁法的频率域阵列电磁数据处理技术,给出了基本数学模型与处理流程;GIUSEPPE 等[34]给出了该方法进行信噪分离的实例。但常规阵列电磁数据处理方法以频域数据删选的方式压制相关噪声的影响[31],效果仍受制于高质量数据在整个观测时段中的长度比例,难以处理持续型的含噪数据,且无法处理含人工源信号的混场源数据。为解决常规电磁数据处理方法输入端相关噪声难以压制的瓶颈问题以及输出端单站处理难以满足阵列观测数据处理需求的问题,本文作者提出一种阵列电磁数据处理新模型。假设多种电磁场源同时入射地球表面,多个测站同步观测电磁场各分量,基于电磁勘探系统的线性时不变性,建立多输入-多输出的系统分析方法,以有效识别并分离天然电磁场、不可控人文电磁场以及可控人工电磁场,为频域阵列电磁数据处理提供理论依据。
1 时空阵列电磁勘探模型
假设电磁勘探系统满足线性时不变性[35],并且其输入端同时存在多个不同类型的场源(包括天然电磁场源、人工电磁场源和人文电磁场源),可以随时间变化。即系统输入端在空间上存在多个场源,每个场源对系统都有多个时刻的独立激励,各场源的激励组合线性无关,而非简单重复,构成空间阵列场源在不同时刻对系统的输入时空阵列。输出端存在多个测站,每个测站可包含多种类型的测道,记录电场、磁场、电流密度以及电磁场梯度等分量。各测站同步观测系统对输入端所有场源在不同时刻激励的响应,构成空间阵列测道对系统的输出时空阵列。图1所示为该系统的典型空间部署示意图。
由于系统输入、输出两端在时间、空间这2个维度均呈阵列分布,可称该系统为时空阵列电磁勘探系统。图2所示为该系统的简化示意图,包含多源输入、大地及多道输出3部分,对地电响应的研究可归结为对多场源-多时刻激励-多道接收的系统研究。

图1 阵列电磁勘探系统的典型空间部署示意图Fig.1 Typical spatial deployment of array electromagnetic exploration system

图2 一种阵列输入-阵列输出的电磁勘探系统示意图Fig.2 A schematic of an array input-output electromagnetic exploration system
2 时空阵列方程组
基于图2所示的阵列电磁勘探模型,进行如下假设:
1)主要研究准静态极限条件下的频率域电磁场(如电场、磁场、磁场梯度、电流密度等),不考虑位移电流的影响。
2)系统中包含L个场源,共激励有限长的观测时间T,T 可分为I 个等长的激励时窗;假设第l(l = 1,2,…,L)个场源在第i(i = 1,2,…,I)个时窗内的时域、频域输入极化电流强度分别为sli(t)和Sli(ω)。
3)系统中包含K个测道(包括不同分量的电场、磁场及其梯度分量等)和I个观测时窗;对每个时窗进行傅里叶变换,得到相应的频谱数据。第k(k =1,2,…,K)测道在第i(i = 1,2,…,I)个时窗的时域、频域观测值分别记为xki(t)和Xki(ω)。
4)系统满足线性时不变条件,即大地系统的时域单位冲激响应和频率特性响应不随时窗的变化而变化,并且不同成分的输出信号、输出端噪声满足线性叠加关系。
对于l场源在i时窗内的输入信号sli(t),记第k个测道对应的单位冲激响应为ψkl(t),输出响应为则数字离散线性时不变系统输入与输出间的关系为

其中:*表示卷积;t 和τ 为采样时刻;N 为i 时窗的采样长度。注意ψkl(t)略去了时窗标号i。
由于k 测道处的观测信号xki(t)为所有场源响应的叠加,考虑输出端噪声时,xki(t)可表述为

其中:rki(t)为输出端噪声。
式(2)即为图2所示系统在线性时不变条件下的输入-输出关系。根据卷积定理,频域观测数据Xki(ω)满足
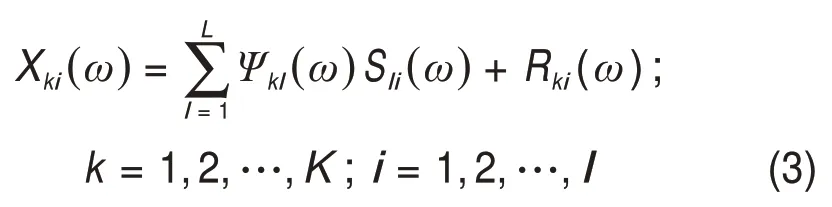
其中:Ψkl(ω)和Rki(ω)分别为频域系统响应、输出端噪声。
由于频率域的各个频点相互独立,并进行独立处理,为了表达方便,下文中均省去频点符号,如将Sli(ω)记为Sli。对上述关系进行整体考虑,将方程写成矩阵形式,有

各矩阵的上角标为其维数。
根据场源类型不同,可对上述关系进行拓展。假设天然场源的个数为L1,未知人文场源的个数为L2,可控人工场源的个数为L3,场源总数L =L1+ L2+ L3。分别以A,B和C标识天然场源、人文场源及可控人工场源的输入矩阵,U,V和W分别为与天然场源、人文场源及可控人工场源相对应的频域系统响应矩阵,则根据系统的线性叠加关系,时空阵列方程组可写为

其中:

各矩阵的上角标为维数,上角标“*”表示矩阵转置。
式(4)和(5)描述了线性时不变电磁勘探系统的输入-输出关系,称为时空阵列方程组。不难理解,Ψ,U,V及W 反映了系统本身的特性以及各激励源的空间信息,与激励源随时窗的变化无关,定义为空间模数矩阵,其中,元素相应称为空间模数(spatial modes)。为方便论述,将时空阵列输入矩阵S,A,B 及C 称为极化参数矩阵,并将其中的元素相应称为极化参数(polarization parameters),将时空阵列输出矩阵X称为时空阵列数据矩阵。在线性时不变电磁勘探系统的基础上,对输入端进行时空阵列激励,对输出端进行时空阵列观测,通过时空阵列方程组描述输入-输出关系;通过直接求解时空阵列方程组,获得场源的极化参数或各测道的空间模数,继而提取场源信息或地电信息,即构成了时空阵列电磁数据处理模型。
需指出的是,与EGBERT[31]所提出的阵列电磁数据处理模型相比,本文模型由系统的线性时不变性推导出时空阵列方程组,并且考虑了存在可控人工源的输入条件,更具一般性。
3 时空阵列方程组求解方案
基于时空阵列电磁数据处理模型,实现时空阵列方程组的求解,可分析场源信息或地电信息。对于电磁勘探,一般更关心地电结构的获取,即从有限规模的观测时空阵列数据矩阵X中提取出地电结构的目标参数(或简称目标参数),如卡尼亚视电阻率,其过程可描述如下:

其中:M为频域的目标参数集合。
考虑采空区充填施工需要排压孔,2个采井先用作排压孔,待采空区充填稳定后,采用级配较好的中粗砂对2个采井回填治理,用振动棒将回填深度内的砂料振捣密实。考虑2个采井较深,先期充填的不规范,治理后还有继续塌陷的可能,井口暂不封堵,采用钢筋混凝土盖板保护,根据塌陷情况,随时回填处理。待塌陷完全稳定后,再用毛石混凝土封堵井口(图4)。
为求取M,可将上述过程分为3 步:第一步,通过观测合理的时空阵列,构建时空阵列数据矩阵X;第二步,利用数学方法,从X 中估计出Ψ,并保障结果的稳健性;第三步,从Ψ 中提取可供解释的目标参数M,需剔除位置信息的影响(如采用各种视电阻率的定义方案以及目标参数的提取方案等)。
对上述第一步,可以利用所有的时空同步观测值构建时空阵列数据矩阵,也可以将数据加以分类以构建不同种类的时空阵列数据矩阵[36],进而得到不同类型的待求解方程组。一般地,根据数据集中主成分的不同,时空阵列方程组可以分为三大类,其解法也有所不同。
3.1 场源极化参数已知
在某些条件下,当观测场中可控人工场占主导,而天然场和人文场能够忽略时,或者利用其他预处理手段能够获得场源极化参数的估计值时,场源极化参数可能为已知信息。
当极化参数矩阵已知时,时空阵列方程组的求解较简单,并可以求得空间模数矩阵的唯一值。假设通过适当的观测方案以及前期处理已获得极化参数矩阵S 的估计,考察时空阵列方程组(4)式可知,在数学上,该式为线性回归模型。
最小二乘法是线性回归模型的经典求解方法,其一般表达式为

其中:上角标“†”表示共轭转置。
对于不相关噪声R,可通过多时窗的叠加进行压制。当观测叠加次数足够多,不相关噪声的平方和叠加极小,即

其中:min表示极小。
3.2 场源极化参数未知
假设时空阵列数据矩阵中天然场占主导,L ≈L1,则时空阵列方程组为

式(9)中,观测数据矩阵X 的维数为K × I,而待求解的空间模数矩阵U的维数为K × L,当I > L时,上述问题在数学上可归为数据降维(dimension reduction)问题。基于特征值求解的方法是数据降维及矩阵分解的主要手段,奇异值分解是最简单和最基本的方法。为了分析方便,以奇异值分解为例,对式(9)的求解进行说明。对矩阵X 进行奇异值分解:
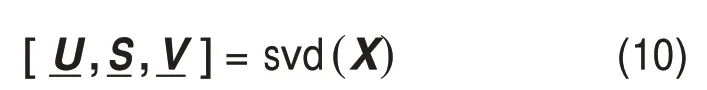
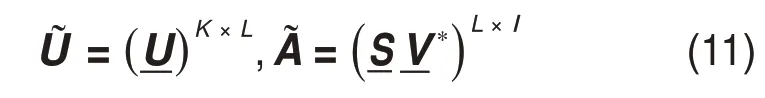
在上述求解过程中,场源数量L 的确定是关键。由于天然场源及不可控人文场源的随机性和不可预测性,很难准确知道其场源个数。一般地,在较宽的观测频段范围内(如0.1~10 000 Hz),天然场源信号可被认为是均匀平面电磁波,其发收距因远大于观测深度及测点距离而可视作相等,不同方向场源的主要能量可以通过分解、合并等效为2个正交水平场源的作用,或者说天然场源的主要极化可等效视作2 个正交水平方向上的极化作用[31]。对于不可控的人文干扰场源,尽管难以确定场源的数量,但实际上无需求解准确的对应于每个人文场源的系统响应,只需求得人文场源的总体信号强度并予以分离即可保障天然场和可控人工场响应估计质量提高。因此,采用主成分分析法评估其等效能量继而估计其等效场源数目及等效场源极化参数是合理的。
需指出的是,由于A未知,时空阵列方程组的分解并不唯一,因为
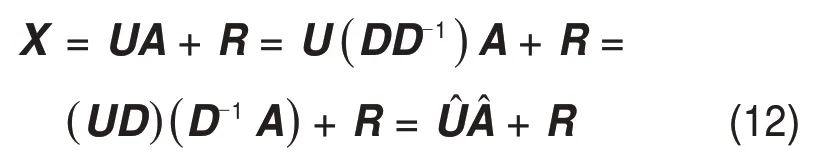
但张量空间模数的转换函数具备唯一性,取

可见,当场源极化参数未知时,应求取张量空间模数的转换函数T,并从T中提取目标参数。
3.3 场源极化参数部分已知
当输入端包含可控人工场源,而观测数据中的天然场或/和人文场也不可忽略时,极化参数部分已知。以包含天然场和可控人工场的时空阵列观测数据集为例,对时空阵列方程组进行讨论。
假设时空阵列数据矩阵中天然场和可控人工场占主导,人文场的影响可忽略,L ≈L1+ L3,则时空阵列方程组为

其中,X 和C 已知,而U,A,W 及R 均未知,并且满足K × I ≥L(K + I)。求解式(14)可采用2 种方法。
一种方式是数学求解。式(14)可写为非线性最小二乘的形式:
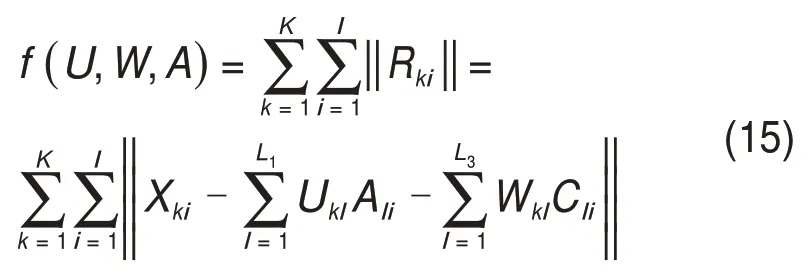
运用非线性最小二乘的分析方法或多变量含误差的统计学方法可对式(15)进行分析求解。另外,由于高频端常处于人工源的远区,其响应一般受非平面波效应影响较小,可获得地电参数的高质量估计值,继而得到稍低频点的W 初始估计值,对式(14)采用迭代计算可有望获得U和W的更高质量估计。
另一种方法是结合物理方法进行求解[36]。由于场源极化参数反映的是场源随时窗的变化,而天然场源的距离远大于观测深度及测点距离空间尺度,可假设一定区域内各测站处的天然场强度随时窗具有相同的变化,即天然场源极化参数相当。在相对安静的地区布设同步远参考测站,保证远参考测站中以天然场信号为主,进而选择合适的数据集,构建主要包含天然场信号的参考观测数据矩阵Xr,可得

其中:Ur和Rr分别为相应的空间模数和输出端的不相关噪声。注意Xr的构建可仅考虑单参考站的2道水平磁场测道,也可视情况加入水平电场和垂直磁场测道,当存在多远参考站时,还可利用多站多道参考数据。
4 目标参数提取方法
针对不同的研究对象,需要获取的解释信息并不一致。如通讯电磁领域常关心场源位置及变化信息,对应地,需求解极化参数矩阵。电磁勘探领域关心的是地球系统本身的结构信息,因此,需求解空间模数矩阵,继而提取目标参数。需指出的是,此处所指的目标参数是指视电阻率、倾子矢量、磁场梯度响应函数等地球物理反演及分析所用的参数,并非真实的地电结构物性参数。目标参数的提取方案主要分为以下两大类。
1)当场源极化参数S及Ψ中包含的空间位置信息(即测点与场源间的距离及相对方位)已知时,可推导出Ψ 与地电参数(σ,ε,μ,η)间的显性表达式,继而通过对Ψ 求反函数的方式获得目标参数的定义:
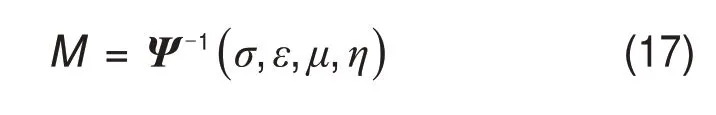
2)当S及Ψ中包含的空间位置信息未知时,无法从Ψ 与地电参数(σ,ε,μ,η)间的关系中获得目标参数的定义,此时,可先求取转换函数T:

其中:Ψ1和Ψ2分别为2 种类型的空间模数张量。根据式(13),T 具有唯一性,不再包含时变场源极化信息的影响。
通过合理定义,可从T中获取目标参数[36]:

其中:函数f表示M与T间的映射关系,如以同一测站的电场和磁场空间模数张量求取阻抗张量、以不同测站的电磁场空间模数张量求取站间转换函数等。
需说明的是,若系统中包含的可控人工场源极化方向单一,则由于方程组求解得到的人工源空间模数仅对应于单一方向,此时可提取人工源的标量参数,如场分量视电阻率、标量阻抗视电阻率等。
5 案例分析
基于本文提出的模型开展了数值模拟试验[36],论证了模型的可行性。2018年7月,在青海柴达木盆地大柴旦地区开展了实际观测与处理试验。试验区地处戈壁滩,人文背景噪声较低,是较理想的电磁观测与处理试验场地。为模拟多场源环境,在试验区中心点约2 km 外采用加拿大凤凰公司的V8 可控源发送机间断发送不同频率的方波信号。接收端同时投入5台设备,观测4个同步阵列测站与1个远参考站,远参考站距试验区约100 km。每个测站均以音频大地电磁法观测方式进行水平张量观测,响应频率范围为1~104Hz,观测时间达200 min。
本例中,假设外加人工源信号场源未知,以模拟未知人文场源。依据本文所述的时空阵列电磁数据处理模型,可建立时空阵列方程组。基于前述方程组求解方案,采用差分求解策略[37],以4个测站的水平磁场差分数据提取未知人文场源极化参数,以远参考站的多测道阵列数据提取天然场源极化参数,继而求解空间模数及目标参数(阻抗视电阻率、相位)。为进行对比,还对观测数据进行常规数据处理。
观测阵列中某测点处理结果如图3所示,其中图3(a)和图3(c)所示为常规稳健估计处理结果,图3(b)和图3(d)所示为时空阵列电磁数据处理结果。从图3 可以看出:试验点常规处理结果视电阻率-相位曲线(ρxy,φxy)在1~30 Hz处产生了畸变,为典型的“近源型”畸变曲线[3],显然是受到了外加人工场源的影响;视电阻率-相位曲线(ρyx,φyx)没有明显“近源型”畸变,其原因是人工源极化方向单一,对该模式方向的电磁场影响较弱,但ρyx和φyx曲线仍有脱节及“飞点”现象,数据显然存在偏差。而采用时空阵列电磁数据处理方法所得到的结果,不再表现出“近源型”畸变形态;ρxy曲线低频段的虚假高阻异常得到了压制,反映出该地深部地层的低阻特征,5~100 Hz频段内相位曲线趋于0的畸变数据得到了校正,相位数据恢复正常;ρyx曲线在10 Hz 附近频段的脱节及“飞点”得以校正,曲线整体更光滑,相位曲线低频段趋于0的畸变数据也得到了校正,5 Hz以上的相位均恢复了正常,结果更合理。对比常规处理结果,本文方法对含相关噪声明显的ρxy,φxy低频畸变数据进行了恢复,对含噪相对不明显的ρyx,φyx数据质量进行了改善,取得了更可信的效果。需指出的是,在低频端数个频点处,即使按本文方法处理,结果也仍存在“飞点”,其原因是:低频端处于大地电磁的“死频带”范围内,信号强度极低;低频端的功率谱数据样本更少,阵列方程组的求解精度相对较低。这也说明在成本允许的前提下,在低信噪比地区,应尽可能延长采集时间,获得更多的低频功率谱,进而提高低频响应估计质量。该实例说明本文所提出的时空阵列电磁数据处理模型具有较好的实用价值。
6 结论
1)提出了一种时空阵列电磁数据处理模型,适用于同时存在天然场源、可控人工源和不可控人文场源的阵列输入条件以及多站、多道、多观测时窗的阵列输出条件。基于电磁勘探系统的线性时不变性推导出了时空阵列方程组,论证了时空阵列方程组的可解性与求解条件,阐述了目标参数的提取方法。本文模型为实现输入端的信噪分离、输出端的多站多道数据综合分析提供了理论依据。
2)时空阵列电磁数据处理模型基于地球电磁系统的线性时不变性,具有广泛的适用性。不同于常规数据处理方法,本文模型将输入端所有能量不可忽略的信号均视为有效信号,继而寻求相应的信噪分离方案,从理论上为相关噪声的压制提供了新思路;通过阵列数据的分类分析,可充分挖掘数据中各类信息,提高数据利用率。
3)本文模型旨在为多输入-多输出的电磁勘探提供一种新的数据分析方案,但并非在所有条件下均适用;模型的可行性和适用性有待进一步论证。对于天然场、人工场和人文场均不可忽略时的场源环境,其时空阵列方程组的高质量求解策略仍需进一步研究。

