光谱特征变量和BP神经网络构建油用牡丹种子含水率估算模型

刘秀英，余俊茹，王世华

（1.河南科技大学农学院，洛阳 471023；2.洛阳市共微生物与绿色发展重点实验室，洛阳 471023；3.洛阳市植物营养与环境生态重点实验室，洛阳 471023）

0 引 言

种子水分是评定种子质量的重要指标之一，通过种子水分测定，能够及时采取措施，防止种子发热、霉变、生虫，避免造成种子变质，是保证种子质量的重要手段[1]。传统测定种子含水率的方法是室内烘干称重法，该方法测定结果准确，但比较繁琐，测定时间较长。其他的直接或间接含水率测定方法虽然也较多，但都存在某些方面的缺点，具有不同的适用范围[2-3]。已有研究表明水分速测仪具有使用简单、测定迅速的特点，但其测试结果的准确性与适宜的温度条件、种子的品种及质量范围有密切的关系[4]。目前，市场上种子水分快速检测设备较多，但多数仪器适合测定特定的品种，需要适宜的工作环境，测定水分的范围因品种而异。且油脂类种子含有不饱和脂肪酸，在研磨、剪切、加热过程中容易氧化，因而较多方法和仪器并不适合进行油脂类种子含水率测定[2]。

近红外光谱分析技术（Near Infrared Reflectance Spectroscopy，NIRS）是20世纪80年代发展起来的一项物理检测技术。与传统分析方法相比，该技术具有检测速度快、非破坏性、无损样品等优点，尤其适用于农产品品质分析[5-7]和食品品质检测[8-9]领域。由于在近红外光谱区，水的O-H基团泛音和组合带非常明显，因此该技术的发展为种子含水率的测定提供了新的方法[10]。国内外学者采用近红外光谱技术结合化学计量学方法特别是偏最小二乘方法对种子含水率的快速检测进行了研究，其估算精度差异较大[10-15]。

人工神经网络具有学习性、容错性、实时性等优点，能够学习和模拟任意复杂的非线性函数，因而被越来越多的应用于可见/近红外光谱分析[13,15-16]。牡丹籽油富含人体需要的氨基酸、维生素、不饱和脂肪酸（含量高达92%以上）等多种成分，其中“植物脑黄金”α-亚麻酸占42%左右[17]，并且油用牡丹种子出油率较高，因此油用牡丹成为了一种新兴的高端木本油料作物。含水率是衡量油用牡丹种子质量、影响牡丹籽油品质的重要指标，因而在销售、储存及加工过程中需要进行快速、准确测量。然而以油用牡丹种子为研究对象，使用BP神经网络模型反演种子含水率的研究目前尚不多见。为此，本研究以油用牡丹种子为研究对象，通过相关分析选择特征变量作为自变量，建立一元线性回归模型，然后将从中优选的参数作为BP神经网络的输入，油用牡丹种子含水率作为输出，建立含水率BP神经网络估算模型，并对比分析一元线性回归（SLR，Simple Linear Regression）模型、逐步多元线性回归（SMLR，Stepwise Multiple Linear Regression）模型、偏最小二乘回归（PLSR，Partial Least-squares Regression）模型和BP神经网络（BPNN，BP Neural Network）模型的估算精度，旨在探索油用牡丹种子含水率高光谱估算的最优模型，提高油用牡丹种子含水率反演精度，为促进中国牡丹产业发展及粮油生产、保障国家粮油安全提供理论依据和技术支持。

1 材料与方法

1.1 供试材料

本研究收集了2个年份（即：2016年和2017年）、不同产地（即：安徽安庆、毫州、铜陵；河南洛阳；山东曹县、吏口、平阴；四川德阳、眉山、资阳）、不同品种（“凤丹”和“紫斑”）的油用牡丹种子 156份。分年份收集种子样品后，首先进行人工目视筛选，选择颗粒比较饱满、大小均匀一致的种子充分进行自然干燥，尽可能的去除种子中的含水率。然后分装在密封袋内，其中，山东曹县、平阴、吏口的种子根据年份、品种不同分成6个平行样，共获得72个样本，设置3个梯度；而其他省份不同地区的样本根据年份、品种不同分成 3个平行样，共获得84个样本，同样设置3个梯度，每份种子样本约30 g，（ 135±10）颗，正好装满75 mm培养皿（见图1），并根据年份、产地、品种不同进行编号。然后将不同梯度样本放入烘箱干燥，通过调节烘干的时间，形成不同的水分梯度，样本含水率范围为 0.22%～5.77%，详细参数见表1。

图1 单个油用牡丹种子样本Fig.1 Single sample of oil tree peony seeds

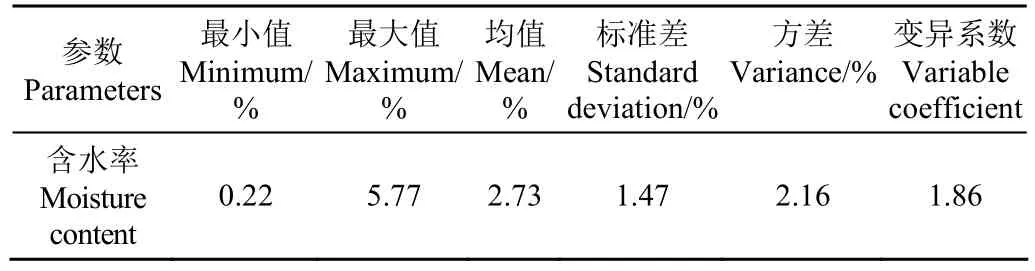
表1 油用牡丹种子样本含水率的统计特征Table 1 Statistical characteristic of moisture content measured oil tree peony seed samples

1.2 测定方法

含水率测定：种子含水率测定采用常压烘箱干燥法，依照GB/T 5009.3—2003进行。

光谱数据采集：采用美国Spectra Vista公司的SVC HR-1024i便携式光谱仪测定置于黑色背景上装满75 mm培养皿的油用牡丹种子光谱，该仪器的光谱范围 350～2 500 nm。在波长350～1 000 nm，光谱分辨率≤3.5 nm；1 000～1 850 nm，光谱分辨率≤9.5 nm；1 850～2 500 nm，光谱分辨率≤6.5 nm。光源为功率50 W卤素灯，光源入射角为 45°；探头视场角为 8°，垂直放置于目标物正上方。仪器开机预热30 min，然后将油用牡丹种子样本装盘，从4个方向对样品进行扫描，每个方向扫描3次，一个样品总共扫描12次，去掉异常线后求平均值作为该样品的光谱值。

1.3 数据处理、模型构建及验证

通过对种子近红外吸收光谱、一阶微分值与含水率的相关分析，选择相关系数绝对值大于0.85的波段即特征波长吸收光谱及其特征波长一阶微分光谱作为自变量构建含水率的一元线性回归估算模型；将水分吸收特征参数与含水率进行相关分析，选择相关系数绝对值大于0.85的参数作为自变量构建含水率的一元线性回归估算模型。为了进一步简化及优化模型，构建BP神经网络模型、多元线性回归模型和偏最小二乘回归模型时，选用的输入变量为构建一元线性回归模型时，建模及验模参数R2大于0.8，验模RMSE小于0.5%，而RPD大于2.5的变量。

为了验证模型的预测精度，采用独立验证样本将模型预测值和实测值进行回归拟合，以预测决定系数（R2）、均方根误差（RMSE）及相对预测偏差（RPD）作为指标评价模型的学习能力和预测能力。RPD值可以解释模型的预测能力，其评价采用 Chang等[18]提出的阈值划分标准。R2及RPD值越大，RMSE越小，表明模型的精度越高。综合建模和验模精度检验结果，选择出最优估算模型。

2 结果与分析

2.1 油用牡丹种子的近红外吸收光谱特征与水分吸收特征

图2和图3为不同含水率油用牡丹种子样本的近红外吸收光谱及吸收特征曲线。由图2可以看出，油用牡丹种子的近红外吸收光谱随含水率增加而增大，在整个波段范围内，光谱曲线总体变化比较明显，具有多个波峰、波谷；此外，光谱曲线具有相似的变化规律，在1 200、1 440、1 930、2 140 nm波长附近有强烈的吸收峰，随含水率增加吸收峰强度具有增大的趋势，而吸收峰位置具有朝长波方向偏移的趋势。依据前人研究可知，1 400、1 900和2 100 nm波长附近的吸收峰是由于水分的强吸收引起的[10,19-20]，因而采用包络线法制作了吸收深度曲线图（图3）。从图3中可以看出，吸收深度最大的波长位于3个水分吸收带，具体位置为1 440、1 930、2 140 nm波长附近。当油用牡丹种子含水率发生变化时，1 930 nm波长处的波段宽度最窄；2 140 nm波长处的吸收深度及吸收面积变化最明显，1 440 nm波长处的吸收深度参数变化最小。因而可以提取1 440、1 930、2 140 nm波长附近的水分吸收特征参数进行油用牡丹种子含水率反演。

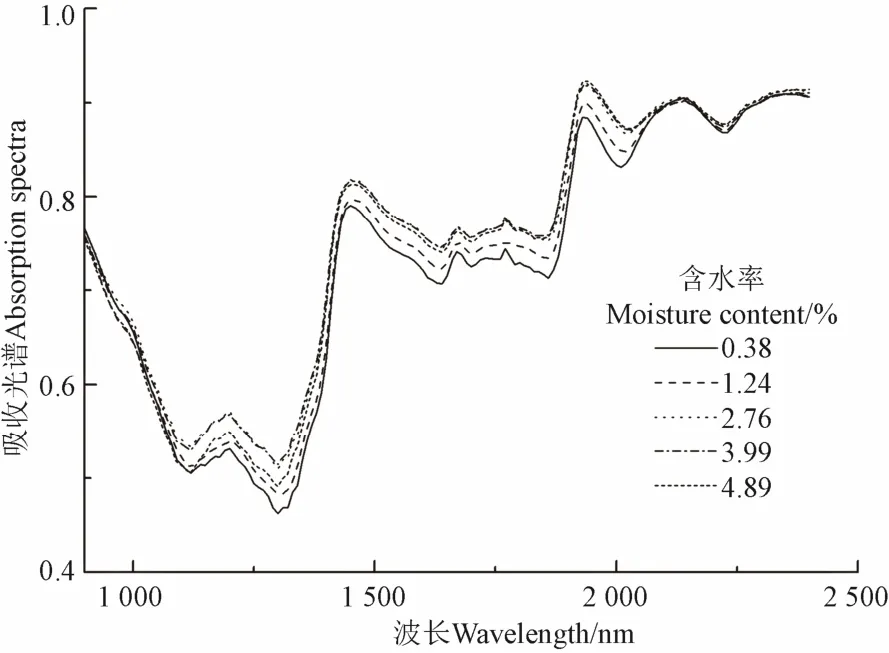
图2 油用牡丹种子的近红外吸收光谱Fig.2 Near infrared spectrogram of oil tree peony seeds

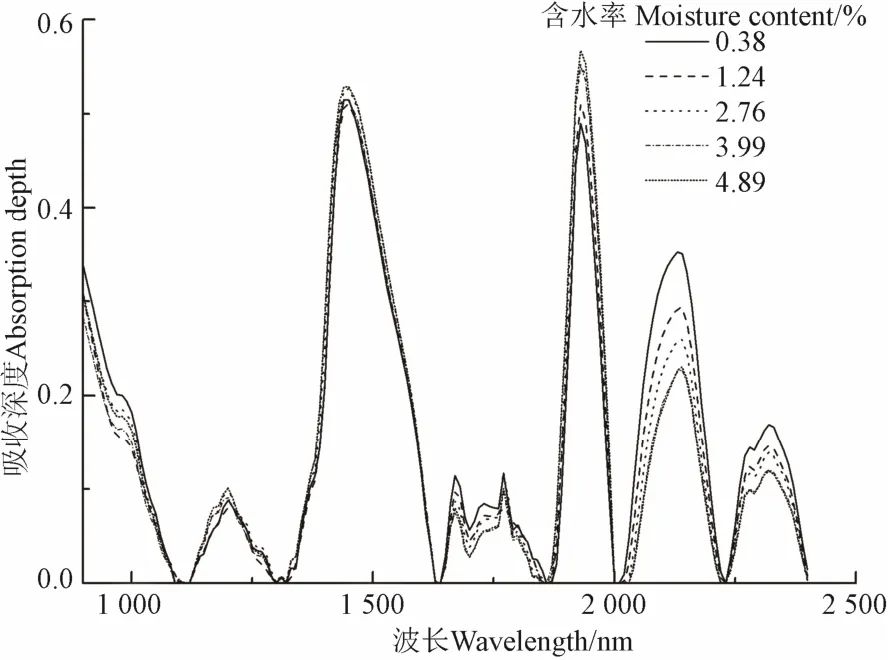
图3 油用牡丹种子的光谱吸收深度曲线Fig.3 Spectral absorption depth curves of oil tree peony seeds

2.2 光谱特征变量选择

对油用牡丹种子近红外吸收光谱及一阶微分光谱与含水率进行相关分析，其相关系数见图4。依据相关系数较大且位于 3个水分吸收带附近的原则，分别选取了 3个特征波长光谱及 3个特征波长一阶微分光谱变量（见图4）用于后续分析建模，其相关系数大小见表2。分析表2可知，特征波长光谱及特征波长一阶微分光谱与含水率的相关性较好，相关系数较高，均通过了0.01极显著性检验。特征波长光谱变量与含水率的相关系数介于0.83～0.90之间，而特征波长一阶微分光谱变量与含水率的相关系数均大于 0.91，介于 0.91～0.96之间，后者的相关性明显高于前者。选择这3个特征波长光谱及3个特征波长一阶微分光谱变量参与一元线性含水率估算模型的构建。

对光谱进行包络线去除后，提取水分吸收特征波段1 440、1 930、2 140 nm处的水分吸收特征参数，包括：最大吸收深度（D）、吸收总面积（A）、吸收峰右面积（RA）、吸收峰左面积（LA）、面积归一化最大吸收深度（AD），及吸收波段波长位置（P）。将提取的吸收特征参数与含水率进行相关分析，其相关系数的大小见表3。从表3可知，除P1930无法计算，LA1440、D2140、RA2140与含水率的相关系数在0.05水平上相关外，其余各参数与含水率的相关性均达到了 0.01水平极显著相关。其中，面积归一化最大吸收深度（AD）与含水率的相关性最好，两者间的相关系数均大于0.9。比较3个波段位置的吸收特征参数与含水率的相关系数可知，2 140 nm波长处的吸收特征参数与含水率的相关性明显优于另外两个波长位置的参数。总体来看，吸收特征参数与含水率的相关系数高于0.85的有7个，说明这些吸收特征参数对含水率变化更敏感，因而选择这 7个吸收特征参数作为变量参与一元线性含水率估算模型的构建。

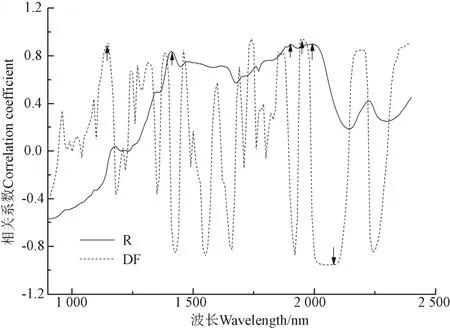
图4 近红外吸收光谱、一阶微分光谱与含水率的相关性Fig.4 Correlation between near infrared absorption spectra and first derivative of spectra and moisture content

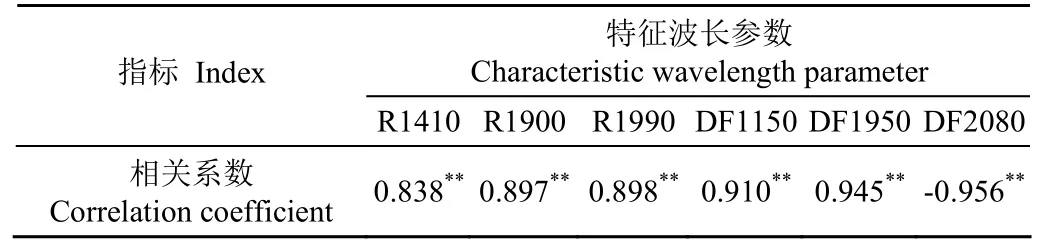
表2 油用牡丹种子特征波长光谱与含水率的相关系数Table 2 Correlation coefficients between characteristic wavelength spectrum of oil tree peony seed and moisture content

2.3 基于近红外光谱的油用牡丹种子含水率估算

2.3.1 含水率的一元线性回归估算模型

建立 13个光谱特征变量与含水率的一元线性估算模型，然后采用独立样本进行验证，其建模及验模参数见表4。分析表4可知，除R1410和S1930这2个变量建立的线性估算模型的验证RPD值小于2.0外，其余变量建立的一元线性估算模型的验证RPD值均大于2.0，校正及验证R2均大于0.75，说明这些变量建立的模型均能用于油用牡丹种子含水率快速、无损检测。3个特征波长一阶微分光谱建立的估算模型效果均较好，建模及验模R2和RPD值均较大，而RMSE值均较小，尤其以DF1950、DF2080这2个参数建立的模型估算效果更佳，其建模及验模R2均高于0.92，RPD值高于4.0，而RMSE值小于0.4%。

表3 油用牡丹种子水分吸收特征参数与含水率的相关系数Table 3 Correlation coefficients between absorptioncharacteristics parameters of oil tree peony seed and moisture content

吸收特征参数中以面积归一化吸收深度参数建立的估算模型效果最好，尤其以AD2140建立的估算模型效果最佳，其建模及验模R2高于0.94，RPD值高于4.0，而RMSE值小于0.4%。综合分析比较一元线性模型的建模及验模的各项参数值可知，以DF2080和AD2140为自变量建立的模型优于其他光谱特征变量建立的模型，都能对含水率进行很好的估算；而且这2个模型建模及验模各项参数几乎相同，相比较而言，以DF2080为自变量建立的模型均方根误差RMSEv较小，而RPDv值较大所以该模型为一元线性模型中的最优估算模型。由于一元线性模型只是应用了一个光谱特征变量建模，为了进一步提高含水率预测精度，依据建模及验模参数R2大于0.8，RMSEv小于0.5%，而RPDv大于2.5的原则，从13个光谱特征变量中进一步优选出 5个光谱特征变量（即 DF1150、DF1950、DF2080、AD1930、AD2140）用于逐步多元线性回归、偏最小二乘回归及人工神经网络建模。

表4 基于光谱特征变量的油用牡丹种子含水率估算模型参数Table 4 The model parameters of moisture content in oil peony seed based on spectral characteristic variable

2.3.2 含水率的BP神经网络模型

以优选出来的5个光谱特征变量（DF1150、DF1950、DF2080、AD1930、AD2140）作为输入层，油用牡丹种子实测含水率作为输出层，隐含层节点数q根据经验公式（1）[21]给定的范围，通过试错法多次训练后选出最佳节点数为5，建立一个网络结构为5-5-1的BP神经网络模型。

式中k为输入层单元数；m为输出层单元数；α为[1，10]之间的常数。

利用Matlab编程进行BP神经网络模型训练，为了使网络在训练阶段容易收敛，首先对输入输出变量进行归一化处理[22]；网络中间层神经元传递函数采用 S型正切函数Tansig，输出层神经元传递函数采用线性函数 Purelin，训练函数为 trainlm[23]。通过 BP神经网络分析得到含水率的预测值，然后对独立验证样本的实测值与预测值进行拟合及精度检验，结果见表5。模型的训练值和目标值均方根误差RMSE为0.220%，相关系数为0.989，相对分析误差RPD值为6.478，模拟结果很好。预测值和实测值的均方根误差RMSE为0.242%，预测值和实测值相关系数达到 0.986，相对分析误差RPD值为5.889，模型预测效果也非常好。综上所述，BP神经网络模型的建模及验证精度都非常高，可进行油用牡丹种子含水率精确估算，几乎可以与实验室测量结果相媲美。

2.3.3 BP神经网络模型与回归模型的比较

将BP神经网络模型与一元线性回归模型、逐步多元线性回归模型以及目前在含水率预测中应用非常广泛的偏最小二乘回归模型进行比较，其结果见表5。为了保证模型具有可比性，建立SMLR模型和PLSR模型时，选取与构建BP神经网络模型相同的自变量（即优选的 5个光谱特征变量 DF1150、DF1950、DF2080、AD1930、AD2140）作为输入变量，并采用相同的独立样本进行验证。表5列出了不同估算模型的建模及验证结果。结果表明，BPNN模型的建模效果最好，建模决定系数R2为0.978，RMSE为0.220%；其次为多元线性模型，建模决定系数R2为0.961，RMSE为0.289%。就模型检验效果而言，BP神经网络模型验证效果仍然最佳，其次为多元线性模型，均优于PLSR模型和一元线性模型。PLSR模型验证决定系数Rv2为0.955，RMSEv和 RPDv分别为 0.242%和 5.889，预测精度略低于 BP神经网络模型和逐步多元线性模型；而一元线性模型无论是建模还是验模效果均最差。但是，一元线性模型仅用了一个光谱特征变量建模，从建模及验模各项参数来看估算效果也比较好，精度比较高。由于该方法最简单且容易操作，在能够满足油用牡丹种子含水率估算的精度情况下，不失为优先选择的估算方法。综合比较4类模型的建模及验模各项参数可知，4类模型的预测精度都比较高，而BPNN模型的预测效果最好，其次是多元线性估算模型。

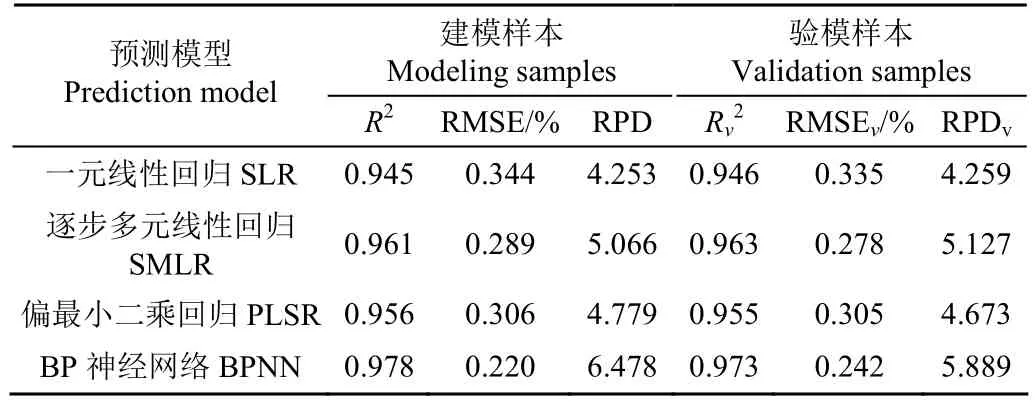
表5 不同估算模型的建模及验证结果Table 5 Modeling and testing results under different estimation

3 讨 论

种子的近红外光谱是其各种组成成分及其内、外结构的综合表现，两者之间存在着密切关系。油用牡丹种子样品中含有大量的C-H、O-H、N-H等含氢基团，因而在近红外光谱图中出现很强烈的吸收，形成吸收峰。但是高光谱数据具有波段多、数据量大、冗余性强等特点，若直接用全波段数据进行数据建模就会导致建模效率低、模型的性能差[24]，因此本研究通过相关分析筛选出了不同油用牡丹种子含水率的敏感波长，有利于构建较高精度的、比较简单的估测模型。将近红外吸收光谱、一阶微分光谱与含水率进行相关分析，结果表明一阶微分光谱与含水率的相关性明显高于近红外吸收光谱。通过相关分析选择了相关系数较大且位于水分吸收波长附近的3个特征波长1 410、1 900、1 990 nm处的吸收光谱，和3个特征波长1 150、1 950、2 080 nm处的一阶微分光谱作为变量，参与一元线性回归建模，结果表明特征波长一阶微分光谱建立的模型预测效果更好，究其原因可能是一阶微处分光谱可以部分消除线性或接近线性噪声的影响[23]。已有研究表明，含水率不同时吸收光谱的吸收峰的位置会产生偏移，通过微分变换可以进一步增强高频信息，因而微分变换可以调整波长光谱，使吸收峰的位置更加明显[10]，同样，通过相关分析可以使不同含水率的吸收光谱的吸收峰的位置更加明显。本研究分析吸收光谱曲线探究水分的吸收峰位置与通过相关分析和微分变换选择的特征吸收峰的具体波段位置虽然稍有差异，但大多都位于1 400、1 900、2 100 nm附近，可见不同方法的分析结果具有一致性。

通过包络线消除法可以去除那些不感兴趣的吸收特征，孤立单个感兴趣的吸收特征，并将其归一到一个一致的光谱背景上，从而具有可以扩大弱吸收特征信息的优势[25]。故本研究采用包络线消除法提取了 1 440、1 930和2 140 nm 3个水分吸收波段附近的18个吸收特征参数，通过相关分析选择了7个相关系数大于0.85的水分吸收特征参数参与一元线性回归分析建模。通过比较分析建模及预测结果可知，3个吸收深度参数为变量构建的模型优于其他吸收特征参数为变量构建的模型；并且2 100 nm波长位置附近的参数（比如：AD2140）建立的模型优于1 400和1 900 nm波长位置附近参数建立的模型。分析原因可能是：从吸收深度图可以发现，不同含水率的种子样本在 2 100 nm波长位置附近吸收峰的吸收深度和吸收面积的变化最明显，说明含水率的变化对这个波长位置的光谱峰值变化影响更大，从而这个位置的参数建立的模型效果更优，这一结论有待进一步研究。

建模方法是影响可见/近红外光谱分析法预测精度的一个主要因素，因此采用多变量校正算法来构建光谱数据与分析目标之间的关系并进行预测精度比较是非常重要的[24]。本研究比较了SLR、SMLR、PLSR和BPNN方法建立的含水率估算模型的预测精度，结果表明 BPNN模型的预测精度最高，其次为SMLR模型，这与其他研究者的结论一致[23,26]。多元回归模型可以实现降维和剔除冗余信息[27]，显著提升光谱分析的精度和可靠性[28]，因而模型的预测精度相对较高。而BPNN模型预测结果优于PLSR模型，原因可能是BPNN模型能够解释光谱变量与含水率间存在的非线性关系，而偏最小二乘回归模型是一种线性算法，没有考虑光谱变量中某些潜在的非线性信息。BP神经网络是一种采用误差反向传播算法对网络权值进行训练的多层前向网络，通过反向传播途径能够不断的调整网络的阈值与权值，直至满足误差最小精度条件，输出最优结果[29]。在数据分析时，理论上BP神经网络模型能够无限逼近任意复杂的非线性函数，因而对非线性问题有很好的解释性。但是，BP神经网络算法的网络权值初始化是随机的，神经网络程序在每次运行后得到的训练结果是不同的[23,30]，因此BP 神经网络学习过程很难取得全局最佳效果。而且BP神经网络的隐含层的层数及节点数对网络的模拟及预测精度影响较大[24]，所以与其他回归模型相比，其在实用性方面还有待于进一步的研究。此外，为了验证所建模型的实用性，下一步将进行另外批次自然含水率的种子验证试验；其次，本研究油用牡丹种子含水率比较低，范围比较窄，为了拓宽模型的适用范围，进一步研究将扩大种子含水率的范围。

4 结 论

本研究针对油用牡丹种子的含水率，采用包络线消除法提取水分吸收特征参数，分析了含水率与近红外吸收光谱、一阶微分光谱及水分吸收特征参数的相关关系，建立了油用牡丹种子含水率估算的一元线性回归模型、逐步多元线性回归模型、偏最小二乘回归模型和BP神经网络模型，并比较了不同模型的预测精度，得出如下结论：

1）通过相关分析确定了含水率的吸收光谱特征波长为 14 10、1 900、1 990 nm，一阶微分光谱特征波长为1 150、1 950、2 080 nm；

2）水分吸收特征参数与含水率的相关性较好，相关系数大于 0.9的水分吸收特征参数为吸收深度参数，即AD1930、AD2140、AD1440；

3）以DF2080和AD2140为自变量建立的一元线性回归模型预测效果明显优于其他模型；

4）将构建一元线性回归模型时筛选出的光谱特征变量作为输入，实测含水率值作为输出，构建含水率估算的逐步多元线性回归模型、偏最小二乘回归模型及BP神经网络模型。其中BP神经网络模型的建模与验模R2分别为0.978和0.973，RMSE分别为0.220%和0.242%，而RPD值分别为6.478和5.889，与其他回归模型相比，BP神经网络模型的建模及验模精度均最高，且比较稳定，是估算油用牡丹种子含水率的最优模型，其次为逐步多元线性回归模型。在能够满足油用牡丹种子含水率估算的精度情况下，一元线性回归模型估算方法可以作为优先选择。