基于“三边”参数的冬小麦冠层SPAD值监测模型

林少喆，彭致功，王春堂，张宝忠，魏征，张倩，韩娜娜，刘露

(1. 山东农业大学水利土木工程学院，山东 泰安 271018； 2. 中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100038)

叶绿素是绿色植株进行光合作用的关键影响因子之一，其含量直接反映绿色植物的营养状态和光合作用能力[1-3]；同时植株叶绿素含量与其氮含量有较高的相关性[4-5]，因此大面积实时无损地监测植株叶绿素含量，对区域作物的长势预测、植株含氮量与产量评估等方面具有重要意义[6].传统叶绿素含量测定多以化学测定法为主，需破坏采样且费时费力[7]；而高光谱技术以其简便、快速、无破坏性、信息量大等优势[8-9]，为实时无损监测作物叶绿素含量提供了重要的技术支撑.

“三边”参数是指基于光谱位置特征的相关变量，即红边、蓝边、黄边.“三边”参数能较好反映绿色植被的光谱特征，且对叶绿素含量变化较为敏感[10-11].史冰全等[12]利用“三边”参数建立了油松林叶绿素含量的估算模型，且模型的决定系数达到了0.788；姚付启等[13]指出了传统红边参数及新红边参数与冬小麦SPAD值在不同生育期均具有良好相关性.由此可以看出利用“三边”参数建立植株叶绿素含量的估算模型是可行的，但是目前采用“三边”参数构建冬小麦叶绿素含量估算模型的研究成果较少.

主成分分析法是一种高维综合评价方法，通过对原有指标进行线性变换和舍弃部分信息，以消除各指标间相互影响，从而提高模型模拟精度.在采用主成分分析方法构建光谱模型方面，朱西存等[14]利用6个光谱指数分别建立了苹果叶片含水量的单参数一元线性回归模型和主成分分析模型，并指出采用主成分分析方法构建模型的模拟精度高于单参数一元线性回归模型，并通过检验样本对主成分模型进行验证，决定系数达0.98；毛罕平等[15]采用主成分分析的方法构建葡萄叶片含水率的估算模型，决定系数达0.94.可见，采用主成分分析法构建光谱模型能提高模型模拟精度与稳定性.

文中以华北平原冬小麦为研究对象，以不同施氮水平下冬小麦植株冠层光谱反射率与植株冠层SPAD值的相关关系为基础，结合不同生育期冬小麦冠层SPAD值与“三边”参数的响应关系，构建基于“三边”参数的冬小麦冠层SPAD值主成分回归监测模型，以期为冬小麦冠层叶绿素含量高光谱诊断提供理论依据和技术支持.

1 材料与方法

1.1 试验区概况

该试验于2017年10月—2018年6月在中国水利水电科学院大兴节水灌溉试验基地进行，该基地属于暖温带半干旱大陆性季风气候，冬春干旱、夏季多雨；年均日照数约2 600 h，多年平均降雨量为540 mm，多年平均气温为12.1 ℃，年无霜期平均为185 d，全年平均水面蒸发量在1 800 mm以上.

1.2 试验设计

供试冬小麦品种为京麦175，设置5个施氮水平处理，分别为N1(不施肥)，N2(150 kg/hm2)，N3(225 kg/hm2)，N4(300 kg/hm2)和N5(375 kg/hm2)，每处理设3次重复，按照随机区组布设.供试肥料为复合肥、尿素，其中播前基肥施复合肥，拔节期追施尿素.各小区灌水量为180 mm，其他农艺管理措施与当地农民的保持一致.

1.3 冠层光谱测定

采用FieldSpec HandHeld 2(ASD)野外便携手持式光谱仪测定冬小麦冠层光谱反射率，视场角为25°，波段范围为325～1 075 nm，光谱采样间隔为1 nm，光谱分辨率为3 nm.在冬小麦生育期内，每隔7～10 d，选择晴朗无云或少云的天气，在10:00—14:00进行冬小麦冠层光谱反射率监测.监测前先对光谱仪进行优化，每次监测前及时采用反射率为1的白板校正，测量时光谱仪探头与地面保持垂直，距植株冠层约15 cm.

1.4 冠层SPAD值测定

冬小麦冠层SPAD值测定与冠层光谱反射率测定同步进行.采用SPAD-502叶绿素仪监测冬小麦冠层SPAD值.各监测样点在测定冠层光谱的区域随机选取2处长势均一的小麦植株旗叶叶片中部进行测定，取其平均值作为该监测样点的冠层SPAD值；每个小区设置3处监测样点，取其平均值作为该小区的冠层SPAD值.

1.5 “三边”参数

共选取具有代表性的20个“三边”参数，分别为“三边”的位置、幅值及面积等9个参数，绿峰与红谷的幅值与位置等4个参数，绿峰与红谷的归一化值与比值等2个参数，以及考虑“三边”面积的比值、差值及归一化值等5个参数，具体见表1[16-17].

表1 选择确定的“三边”参数Tab.1 Select determined ″three-edge″parameters

1.6 数据处理与分析

在冬小麦生育期内共6次SPAD值监测试验，涉及5个处理，各处理设3次重复，共采集90组冬小麦冠层SPAD值样本，对同一处理的3个重复监测冬小麦冠层SPAD值随机以2∶1分为2组，其中60组用于训练建模，30组用于模型验证.

1.7 模型评价指标

采用相关系数(r)衡量冬小麦冠层SPAD值与“三边”参数之间的相关程度.一般认为r的绝对值越大且越接近于1，则两者的相关程度越高.相关系数计算公式[16]为

(1)

为了保证所建监测模型的可靠性与稳健性，将预测值与实测值之间进行拟合，以决定系数R2、均方根误差RMSE及相对误差RE对监测模型进行精度评价；其中R2越大，RMSE和RE越小则说明模型的模拟精度越高[16].

(2)

(3)

(4)

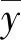
2 结果与分析

2.1 不同施氮水平冬小麦SPAD值变化

不同施氮水平下冬小麦SPAD值变化如图1所示，冬小麦冠层SPAD值在全生育期内先上升后下降，拔节期到抽穗期逐渐上升，在抽穗期达到最大，各处理的平均值为54.4；由于冬小麦在灌浆期之后，营养物质不断向穗部转移，叶片逐渐凋萎、衰落，所以抽穗期到灌浆期SPAD值逐渐下降，并在成熟期降至最小，其平均值仅为23.1.在同一生育期内，SPAD值随施氮水平增高而增大，且不同处理间SPAD值的差异具有统计学意义(P<0.05).

图1 不同施氮水平下冬小麦SPAD值变化Fig.1 Changes of SPAD value of winter wheat under different nitrogen application levels

2.2 “三边”参数与冬小麦冠层SPAD值的相关性

“三边”参数与冬小麦冠层SPAD值的相关系数见表2，在拔节期，红谷位置λv和(SDr-SDb)/(SDr+SDb)具有统计学意义(P<0.01)且相关系数均大于0.6，蓝边面积SDb具有统计学意义(P<0.05)，而其他“三边”参数不具有统计学意义(P<0.05)；在抽穗期，红边幅值Dr、红边位置λr、蓝边位置λb、黄边幅值Dy、黄边位置λy和红谷位置λv不具有统计学意义(P<0.05)，而其他“三边”参数均具有统计学意义(P<0.01)，其中(SDr-SDb)/(SDr+SDb)和(SDr-SDy)/(SDr+SDy)、红谷幅值Rr、黄边面积SDy、蓝边面积SDb，SDr/SDy和绿峰幅值Rg的相关系数均达到0.7以上，且依据相关系数大小依次递减；在灌浆期，红边幅值Dr、红边位置λr、蓝边位置λb、黄边幅值Dy、黄边位置λy、红谷位置λv、红边面积SDr、黄边面积SDy，SDr/SDy，(SDr-SDb)和(SDr-SDy)/(SDr+SDy)不具有统计学意义(P<0.05)，绿峰位置λg具有统计学意义(P<0.05)，其他“三边”参数均具有统计学意义(P<0.01)，其中红谷幅值Rr、绿峰幅值Rg、蓝边面积SDb和(SDr-SDb)/(SDr+SDb)的相关系数均大于0.6，且相关系数依次减小；在成熟期，冬小麦冠层SPAD值与选定的“三边”参数均不具有统计学意义(P<0.05)，且相关系数均小于0.45，因此该生育期内植株衰老凋萎，叶片颜色变黄，且叶绿素含量极低所致，为此在后期叶绿素光谱模型构建中未考虑该生育期.

在全生育期，红边幅值Dr、蓝边幅值Db、蓝边位置λb和蓝边面积SDb均不具有统计学意义(P<0.05)，SDr/SDy具有统计学意义(P<0.05)，而冬小麦冠层SPAD值与其他15个“三边”参数均具有统计学意义(P<0.01)，其中(SDr-SDy)/(SDr+SDy)、红谷位置λv、(Rg-Rr)/(Rg+Rr)和(SDr-SDb)/(SDr+SDb)的相关系数均大于0.82，且相关性依次递减.

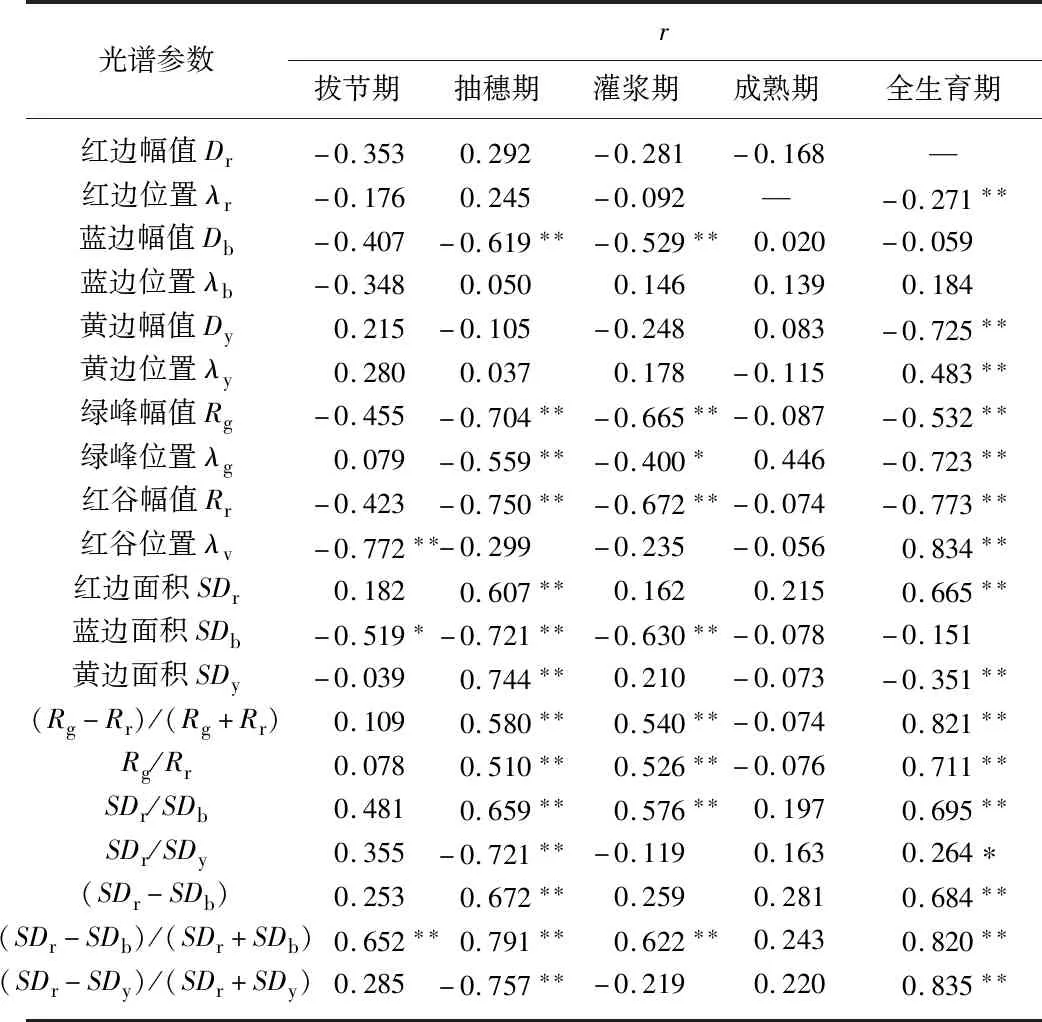
表2 “三边”参数与冬小麦冠层SPAD值相关系数Tab.2 Correlation coefficient between ″three-edge″ parameters and SPAD value of winter wheat canopy

2.3 冬小麦冠层SPAD值光谱模型构建

以相关系数最高为原则，筛选出拔节期为红谷位置λv、抽穗期为(SDr-SDb)/(SDr+SDb)、灌浆期为红谷幅值Rr、全生育期为(SDr-SDy)/(SDr+SDy)作为自变量，以各生育期及全生育期的冬小麦冠层SPAD值为因变量，构建了基于“三边”参数的冬小麦冠层SPAD值一元线性回归模型；选择各生育期全部“三边”参数(20个)为自变量，冬小麦冠层SPAD值为因变量，采用主成分分析的方法构建各生育期的冬小麦SPAD“三边”参数估算模型.

首先将变换后的数据进行标准化处理；以特征值F大于1及累计贡献率Rc大于80%为原则筛选主成分因子数，确定每个关键生育期的主成分因子数均为4个(Z1，Z2，Z3，Z4)，见表3，表中Rσ为方差贡献率，其中拔节期、抽穗期、灌浆期和全生育期的累积贡献率分别为84.8%，85.1%，84.6%和85.5%，构建基于主成分的冬小麦冠层SPAD值监测模型可以代表84%以上光谱信息；其次通过多元回归方法构建冬小麦SPAD值与主成分(Z1,Z2,Z3,Z4)的回归模型，获得主成分回归的系数；把主成分回归系数转化为标准化因变量对标准化自变量回归方程的系数；最后把该系数转化为原因变量对原自变量的回归系数.冬小麦不同生育期冠层SPAD值与“三边”参数的一元线性回归模型和主成分回归模型如表4所示.

表3 各生育期特征值与累积贡献率Tab.3 Characteristic value and cumulative contribution rate of each growth period

表4 基于“三边”参数的冬小麦冠层SPAD值估算模型构建Tab.4 Estimation model of SPAD value of winter wheat canopy based on ″three-edge″ parameters

在拔节期和灌浆期，分别以红谷位置和红谷幅值的相关系数最大；600～700 nm范围是叶绿素吸收最强的光谱带属红橙光，其中以670 nm处“红谷”的叶绿素吸收达到最大；在抽穗期和全生育期，分别以(SDr-SDb)/(SDr+SDb)和(SDr-SDy)/(SDr+SDy)的相关系数最大，因叶绿素含量最敏感的波段范围位于可见光波段，叶绿素吸收谷位于黄绿光波段，而红光区域与蓝光区域是叶绿素含量的强吸收区域[17]，且红边是植株叶绿素含量的特性指标[18]，因此SPAD值与红边面积、黄边面积、蓝边面积组成的光谱指数有很强的相关性.为此，在拔节期，以红谷位置λv为参数建立一元线性回归模型的决定系数R2为0.546，基于“三边”参数建立的主成分回归模型的决定系数R2为0.715；在抽穗期，以(SDr-SDb)/(SDr+SDb)为参数建立一元线性回归模型的决定系数R2为0.626，基于“三边”参数建立的主成分回归模型的决定系数R2为0.660；在灌浆期，以红谷幅值Rr为参数建立一元线性回归模型的决定系数R2为0.452，基于“三边”参数建立的主成分回归模型的决定系数R2为0.483；在全生育期，以(SDr-SDy)/(SDr+SDy)为参数建立一元线性回归模型的决定系数R2为0.698，基于“三边”参数建立的主成分回归模型的决定系数R2为0.813.与一元线性回归模型相比，主成分回归模型在不同生育阶段以及全生育阶段的决定系数R2均有所提高表明，采用主成分回归模型的模拟精度优于一元线性回归模型.

2.4 模型验证

冬小麦冠层SPAD值监测模型模拟验证效果见表5，在拔节期主成分回归模型模拟的决定系数R2为0.419，均方根误差RMSE为3.270，相对误差RE为7.55%，其中决定系数R2较同期一元线性回归模型提高49.6%，均方根误差RMSE和相对误差RE均降低9.0%；在抽穗期主成分回归模型模拟的决定系数R2为0.816，均方根误差RMSE为4.163，相对误差RE为7.80%，其中决定系数R2较同期一元线性回归模型提高54.3%，均方根误差RMSE和相对误差RE均降低12.4%；在灌浆期主成分回归模型模拟的决定系数R2为0.617，均方根误差RMSE为4.936，相对误差RE为9.62%，其中决定系数R2较同期一元线性回归模型提高14.3%，均方根误差RMSE和相对误差RE均降低13.5%；在全生育期主成分回归模型模拟的决定系数R2为0.782，均方根误差RMSE为7.109，相对误差RE为15.64%，其中决定系数R2较同期一元线性回归模型提高8.6%，均方根误差RMSE和相对误差RE均降低13.6%.由此可见，基于主成分分析方法构建的冬小麦冠层SPAD值估算模型的模拟效果均优于一元线性回归模型.

表5 冬小麦冠层SPAD值监测模型验证评价指标Tab.5 Validation and evaluation index of SPAD value monitoring model for winter wheat canopy

3 结 论

以冬小麦各生育期植株冠层SPAD值与“三边”参数之间的相关性为基础，构建了基于“三边”参数的冬小麦分生育期植株冠层SPAD值的一元线性回归模型和主成分回归模型，并对各模型监测效果进行验证.得到以下主要结论：

1) 在拔节期、抽穗期、灌浆期和全生育期分别以红谷位置、(SDr-SDb)/(SDr+SDb)、红谷幅值、(SDr-SDy)/(SDr+SDy)的相关系数最高，且均具有统计学意义(P<0.01).

2) 在基于“三边”参数的冬小麦冠层SPAD值一元线性回归模型中，除拔节期的决定系数R2仅为0.280外，抽穗期、灌浆期和全生育期的决定系数R2分别为0.529，0.540和0.720.

3) 选取全部“三边”参数建立冬小麦冠层SPAD值主成分回归模型，在拔节期、抽穗期、灌浆期和全生育期的决定系数R2分别为0.419，0.816，0.617和0.782，表明构建综合光谱参量的冠层SPAD值监测模型在各生育时段都具有较高的估算精度.

4) 与冬小麦冠层SPAD值一元线性回归模型相比，主成分回归模型在拔节期、抽穗期、灌浆期、全生育期的决定系数R2分别提高49.6%，54.3%，14.3%和8.6%，均方根误差RMSE与相对误差RE均分别减少9.0%，112.4%，13.5%和13.6%，表明采用主成分回归模型的模拟精度优于一元线性回归模型.