基于辨识模型结构简化的直升机气动参数频域辨识研究

石佳伟，刘峻豪

基于辨识模型结构简化的直升机气动参数频域辨识研究

石佳伟，刘峻豪

（中国飞行试验研究院飞机所，陕西 西安 710089）

在直升机频域参数辨识中，辨识模型作为辨识的基础，其结构的合理性会对辨识结果的精度产生较大的影响。对频域辨识模型的结构简化问题进行研究，分析了辨识模型结构简化的机理，并归纳总结出模型结构简化的方法。最后通过算例，验证了辨识模型结构简化方法的正确性，以期为直升机频域参数辨识提供一定的指导建议，具有较大的工程应用价值。

辨识模型结构简化；辨识参数；频率响应；频域辨识

1 引言

在以往的直升机频域参数辨识中，通常采用优化辨识算法、提升试飞数据质量等方式提高辨识结果精度，对辨识模型结构的简化研究较少。但辨识模型作为频域参数辨识的基础，其结构是否合理，实际上对最终的辨识结果影响较大。简单而言，当直升机飞行试验的操纵输入被充分激励，且不存在单通道激励输入多通道响应输出时，辨识模型中的所有参数都能够进行辨识。但在实际试飞过程中，由于飞行控制系统的介入，单通道的扫频激励输入往往会出现多通道响应输出，即通道间具有强相关性，加上驾驶员的扫频输入频谱存在不完善等问题，都会导致部分测量参数得不到预期的频率响应，从而导致获取的谱信息不够丰富。由相关性准则可知，当输入激励与测量参数响应信号的相关性低于0.6时，属于所考虑的频率范围内，该参数得到的频率响应数据质量较差，包含的频率信息量过少，这样的频率响应数据应当剔除，无法用于频域参数辨识。如果仍按照原模型结构继续辨识，会导致辨识模型中，部分参数没有频率响应数据支撑，则辨识得到的气动参数精度将大大降低，甚至不可信[1-2]。因此，本文将对辨识模型结构简化问题开展研究，基于数据质量对辨识模型中的部分参数进行剔除，使辨识的模型更为可信，并归纳总结出待辨识模型结构简化的方法，对开展直升机频域参数辨识提供一定的帮助。

2 辨识模型结构的简化

因条件有限，本文仅获得了悬停状态下的直升机扫频数据，因此，在模型结构简化中，将以悬停状态下的数据为例。本文将从2个方面开展待辨识模型结构简化的研究：①为建立频率响应数据与待辨识参数的关系，从而确定辨识前应该剔除的不可辨识参数；②为研究辨识过程中参数整定的问题，即部分待辨识参数虽然有数据支撑，但数据质量一般，在辨识过程中敏感性、精度较差，因此，将这部分参数剔除或固定，能够优化整个辨识模型，提高辨识精度。

2.1 频率响应数据与待辨识参数的关系

通常情况下，在频域参数辨识中，为了避免机体轴向速度数据质量较差，无法用于辨识，而导致的辨识精度下降，一般需要引入机体的三个轴向加速度数据参与频域辨识。因此，可得纵向通道将有、、、、a、a六个参数对1（旋翼纵向周期变距）和（旋翼总距）控制量的频率响应，横航向通道将有、、、、y五个参数对1（旋翼横向周期变距）与（尾桨总距）控制量的频率响应。想要通过对频率响应数据的筛选来确定辨识模型的结构，就必须建立频率响应数据与辨识模型结构中参数的对应关系。

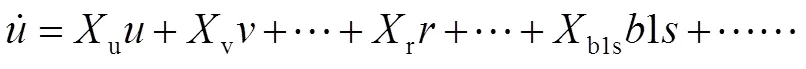
同理，可以建立纵向、横航向通道中，其他数据的频率响应与辨识模型中参数的对应关系，整理结果如表1和表2所示。

表1 纵向数据的频率响应与辨识模型中气动导数的对应关系

频率响应控制性导数稳定性倒数 u/bls、ax/blsXblsXq、Xu w/bls、az/blsZblsZq、Zu q/bls、θ/blsMblsMq、Mu u/thte、ax/thteXthteXw w/thte、az/thteZthteZw q/thte、θ/thteMthteMw

表2 横航向数据的频率响应与辨识模型中气动导数的对应关系

频率响应控制性导数稳定性倒数 v/als、ay/alsYalsYp、Yv p/als、φ/alsLalsLp、Lv r/alsNalsNp、Nv v/thtr、ay/thtrYthtrYr p/thtr、φ/thtrLthtrLr r/thtrNthtrNr

如表1、表2所示，建立起纵向、横航向频率响应数据与辨识模型结构中参数的对应关系。在计算飞行试验数据中各组频率响应后，如果其频率响应的相干值较差时，总低于0.6，则不能用于频域辨识，可以按照上述方式，对辨识模型中的参数进行剔除，从而确定模型，提高模型辨识精度。

在辨识模型结构简化中，如果剔除的数据越少，则频域辨识的结果越准确，精度越高；如果剔除的数据越多，则频域辨识的结果越失真，精度越差。工程经验表明，当剔除的频率响应数据达到待辨识频率响应数据的一半以上，则辨识精度将大大降低，辨识结果也将不可信。所以，要求可用于频域辨识的频率响应数据必须要达到待辨识频率响应数据的一半以上。

在通过筛选频率响应数据来剔除辨识模型中的气动参数时，辨识模型状态矩阵主对角线上的参数作为辨识模型的主要气动导数，不能进行剔除，否则将严重影响辨识的结果与精度。

综上所述，当可用于频域辨识的频率响应数据没有达到待辨识频率响应数据的一半以上，或需要对辨识模型状态矩阵主对角线上的参数进行剔除时，都表明该试飞数据的频率响应是较差的，不能用于频域辨识，需要选取新的飞行试验数据进行计算。

2.2 参数整定

在频域参数辨识中，一般是通过计算代价函数ave，即辨识模型频率响应函数与试飞数据频率响应函数的频率响应误差，从而迭代计算出气动参数。为了便于对其进行优化，计算代价函数的矩阵，它表示代价函数对每个辨识参数变化的曲率，其中Θ表示辨识参数矢量，矢量中共有p个待辨识参数，即：

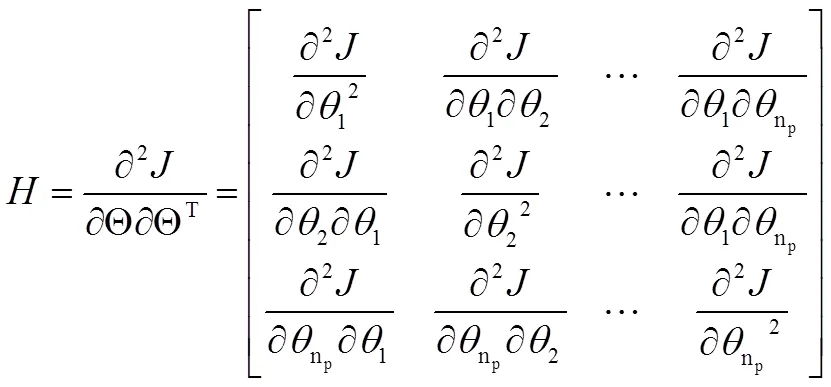
在这里引入两条状态方程辨识的准则[3]，即不敏感性值与精度边界值。不敏感性值则由矩阵中对应的对角元素确定，精度边界值由矩阵的逆阵中对应的对角元素确定。

不敏感值表征结构中某一参数的变化，对整个辨识结构中代价函数收敛的影响程度，不敏感值越小其影响程度越小。精度边界值表征着结构中某一参数的变化，对整个辨识结构可辨识性及精度的影响程度，精度边界值越小，可辨识性越好，精度越高。经过反复迭代计算发现，当不敏感性值小于10%，精度边界值小于20%时，平均代价函数即能满足要求。如果简化后的辨识模型在计算过程中，部分参数的不敏感性值总大于10%，或者精度边界值总大于20%，则需对这部分参数进行固定或者剔除。

3 算例验证

以直升机纵向线性化小扰动辨识模型作为算例，选择某型直升机操纵性与稳定性飞行试验中获取的悬停状态下扫频数据作为辨识数据，通过第二节模型结构简化的方法，进行频域参数辨识，并通过时域验证。辨识模型如下所示[4]：

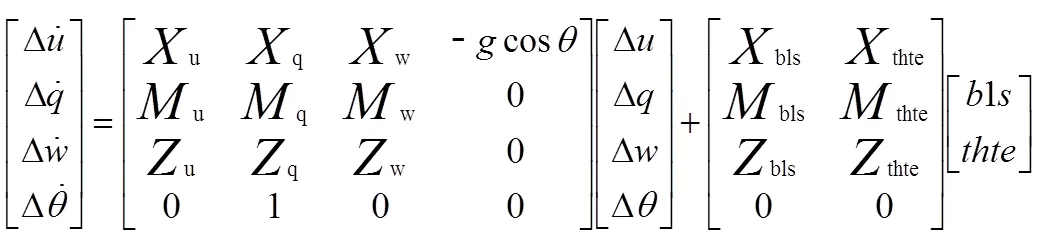
计算试飞数据的纵向通道频率响应如图1所示。

从图1中可以看出，1与之间的相干函数在关心的频率范围内均低于0.6，表明数据质量较差。

/1的频率响应如图2所示。

从图2中可以看出，1与在0.7～9.5 rad/s的范围内，相干值均高于0.6，表明在这个范围内，数据质量较好。

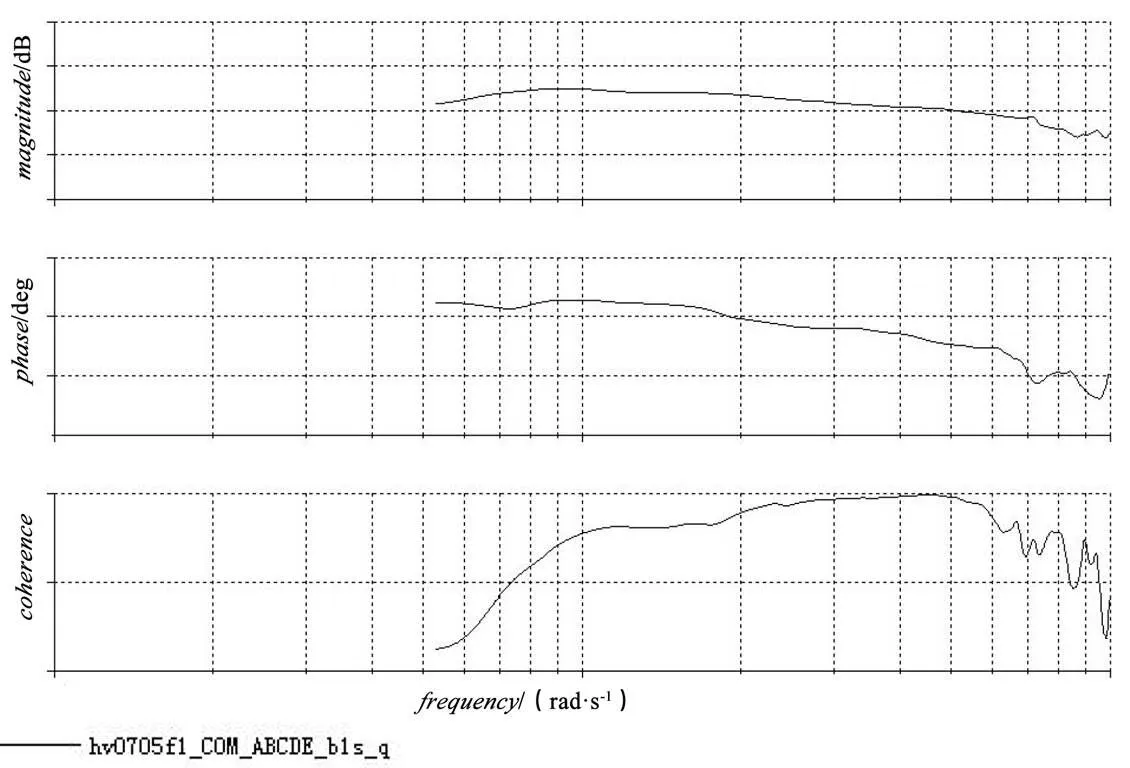
图2 q/b1s的频率响应

诸如此类，在纵向通道的十二对频率响应中，有一些部分频率响应的相干值在所关心的频率范围内，几乎都低于0.6的，则对这些频率响应选择剔除，不使用其频率响应函数进行参数辨识。其他频率响应在所关心的频域范围内，相干值也不全高于0.6，对这部分频率响应对进行频率截取，只选择相干值高于0.6，且连续的部分用于参数辨识。

经过筛选，在获得的十二对频率响应数据中，只有/1、/1、x/1、z/1、x/、z/这六对频率响应数据可用，采用2.1节中模型结构简化的办法，剔除w、thte两个参数，确定辨识前模型的结构。再经过2.2节中参数整定的方法，剔除u、u，thte并将u、q、q的值固定下来，其计算结果如表3所示。

表3 直升机纵向气动参数辨识结果

参数名数值精度边界值/（%）不敏感性值/（%） Xq﹣0.593 05—— Xu﹣0.008 85—— Xw﹣0.144 165.8822.137 Mq﹣0.451 496.8912.561 Zq﹣0.409 72—— Zw﹣0.185 9216.016.940 Xbls1.852 35.9012.655 Mbls﹣2.194 653.7791.360 Zbls1.353 756.2433.086 Zthte﹣33.136 053.7731.718

将表中气动参数以矩阵的形式表示，其最终结果为：

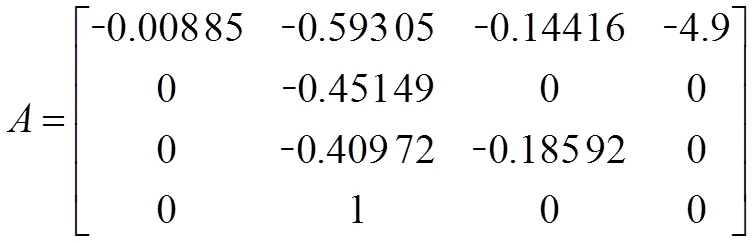
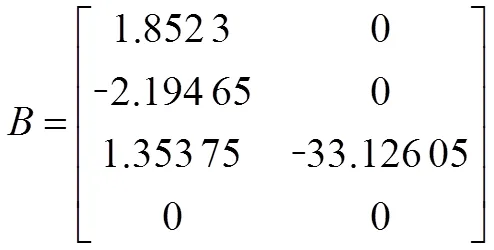
阵中气动参数为直升机纵向通道的稳定性导数，阵中气动参数为直升机纵向通道的控制性导数。从矩阵中的数据可知，频域辨识的结果中，主对角线上参数的极性与实际的气动参数相同，数值也都在同一个量级上，较为可信。

时域验证中，最好选择用与扫频输入非相关的脉冲输入等其他方式作为输入量，所以在时域验证的数据中，截取一段脉冲输入作为时域验证的试飞数据，并用这段试飞数据的操纵输入量去激励辨识模型，获得辨识模型仿真的结果。具体验证结果如图3所示。图3为纵向速度、垂向速度、俯仰角以及俯仰角速率的时域验证对比图。从图中可以看出，纵向速度、俯仰角以及俯仰角速率辨识模型的预测的响应与飞行试验数据吻合度很高，响应趋势也基本一致。垂向速度吻合度略有不足。这是因为飞行员在悬停状态下做纵向扫频激励动作时，直升机自身的激励运动引发的一定程度上垂向运动，最终导致所获取的数据在垂向上质量较差。

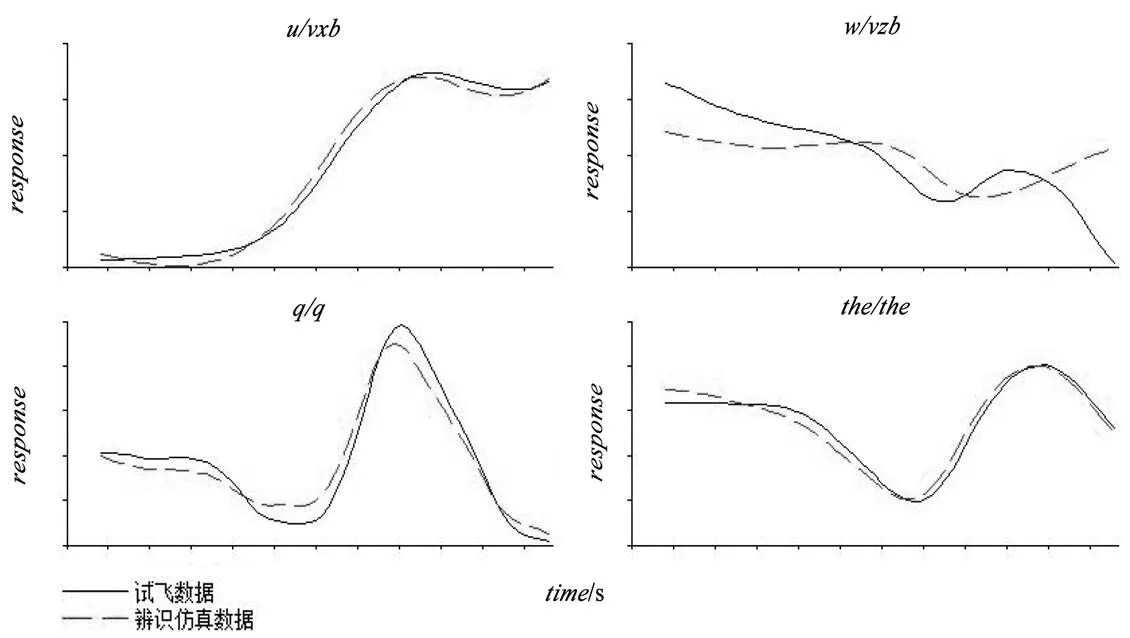
图3 u、w、q、the的时域验证结果

总体而言，辨识得到直升机纵向辨识模型能很好地预测直升机在此飞行条件下的动力学响应特性，所以能够得出辨识模型结构简化的方法是正确的、可信的。

4 结束语

频域参数辨识是直升机飞行试验中获取气动导数的重要方式之一，本文通过对待辨识模型结构进行简化，从而提高整体辨识精度，得到较为准确的气动导数，对开展飞行试验具体重要意义。由于条件与时间有限等原因，本文仅对解耦后的直升机线化小扰动模型进行了简化，总结出其模型结构简化的方法，但针对九阶纵横耦合模型未进行深入研究。因此，希望在以后的研究中，能够在本文研究的基础上，进一步开展高阶模型的结构简化研究工作。

［1］张怡哲，左军毅，张培田.飞机和旋翼机系统辨识：工程方法和飞行试验案例［M］.北京：航空工业出版社，2012.

［2］李富刚，石佳伟，王文星.基于试飞数据的直升机气动模型参数频域辨识［J］.航空科学技术，2018（9）：37-42.

［3］MAINE R E，ILIFF K W.Theory and practice of estimating the accuracy of dynamic flight-determined coefficients［D］.NASA R P 1077，1981.

［4］张毅，袁东.直升机气动与操纵导数的频域辨识方法研究［J］.飞行力学，2012（4）：310-313，327.

V212

A

10.15913/j.cnki.kjycx.2021.01.011

2095－6835（2021）01－0034－03

石佳伟（1992—），男，回族，陕西镇安人，硕士，工程师，研究方向为飞行性能品质。刘峻豪（1996—），男，硕士，工程师，研究方向为飞行性能品质。

〔编辑：张思楠〕