基于GNSS水准和重力场误差特性的大地水准面精度评估方法

章传银，马 旭，章 磊，丁 剑

1. 中国测绘科学研究院，北京 100036； 2. 国家测绘产品质量检验测试中心，北京 100036

目前，大地水准面精度评估普遍采用实测GNSS水准数据，主要方法可归纳为两类：一类通过统计GNSS水准高程异常与重力地面高程异常之间的差异，来评价重力大地水准面成果的质量[1-6]；另一类是所谓的GNSS水准外部检核方法，以未参与融合或外业实测的GNSS水准点为检核点，通过比较检核点实测高程异常与融合后的地面高程异常之间差异，来评估大地水准面成果的精度[7-8]。

先来分析第一类评估方法的合理性。重力地面高程异常，按全球积分确定或精化，中长波精度高，短波超短波精度低。GNSS水准点的正常高，按水准方法传递，误差沿水准路线累积，导致GNSS水准高程异常的中长波误差大。显然，中长波误差大的GNSS水准高程异常，无法有效评估中长波精度高的重力地面高程异常。

再分析GNSS水准外部检核方法的有效性。由于检核点正常高无可避免地要以参与融合的GNSS水准点起算(或误差强相关)，因此，检核点高程异常与融合后的地面高程异常之差，只是检核点与其距离最近GNSS水准点之间的高程异常差，所得精度指标，显然不能代表实用地面高程异常精度。本文将采用距离等于GNSS水准点平均间距的两点实用高程异常差的标准差(简称实用地面高程异常内部误差)来表达这种精度。

可见，已有方法难以有效评价大地水准面的精度，这已成为高程基准现代化及其成果应用面临的关键问题[6]。本文基于GNSS水准高程异常与重力场频域误差特性，分析GNSS水准与重力地面高程异常融合的技术要求，研究大地水准面成果的误差表达与精度评估方法。

1 GNSS水准与重力地面高程异常误差特性及其融合要求

区域似大地水准面精化计算一般分两步进行[1，5]：第1步，由重力场数据，按边值问题解的积分方法，精化重力地面高程异常；第2步，将GNSS水准高程异常与重力地面高程异常融合，生成实际应用的地面高程异常(简称实用地面高程异常)。

1.1 GNSS水准与重力地面高程异常的频域误差特性

GNSS水准点的正常高，按水准高差逐站传递方法测定。由于水准视线直接置于当地水准面中，因而距离较近的两点间正常高差一般具有很高的精度。但是，水准传递误差沿路线累积，势必导致长距离两点间的正常高差误差较大。忽略GNSS大地高差误差，两点间GNSS水准高程异常差的精度一般随两点间距离的增大而降低。这表明，短距离两点间GNSS水准高程异常差的精度高，长距离的误差大。

重力地面高程异常，是地球重力场外部边值问题解，由重力数据经全球积分间接确定或精化，中长波精度高、短波超短波误差大，即空间尺度越小，相对误差越大。在局部地区一般表现为两点间重力地面高程异常差的误差不随距离增大而出现明显变化。

1.2 GNSS水准与重力地面高程异常融合的技术要求

由上述GNSS水准与重力地面高程异常的频域误差特性，不难理解，有效合理的GNSS水准与重力地面高程异常融合方法应满足如下技术要求：

(1) 融合算法能有效整合重力地面高程异常的高精度中长波成分与实测GNSS水准高程异常高精度短波成分。

(2) 实测GNSS水准高程异常的贡献，随空间距离增大逐渐减弱；重力地面高程异常的贡献，不随空间距离增大发生明显变化。

(3) 在误差处理方面，能同时有效抑制短波重力地面高程异常误差，控制长距离实测GNSS水准高程异常误差的累积。

已有的大地水准面精度评估和GNSS水准融合方法，还未能顾及GNSS水准和重力地面高程异常误差在频域上的互补性质及融合的技术要求。关于GNSS水准与重力地面高程异常有效融合算法研究，已超出本文的讨论范畴。

2 似大地水准面成果的误差估计与精度评估方法

2.1 似大地水准面成果的误差估计方法

为有效利用GNSS水准和重力地面高程异常误差在频域中的性质，需要采用统计分析技术，构造似大地水准面成果误差估计的一般方法[8-9]。

对于相距L的两个GNSS水准点，令两点间GNSS水准高程异常差为ΔζGNSSl，误差为σGNSSl，重力地面高程异常差为ΔζGrav，误差为σGrav；GNSS水准残差高程异常差(即GNSS水准高程异常差与重力地面高程异常差之差)d=ΔζGNSSl-ΔζGrav，误差为σd。文中的误差一般用1倍标准差(RMS)表示，下同。按误差传播定律有

(1)

(2)

式中，a为GNSS基线大地高差的固定误差，b为比例误差系数，由GNSS定位结果给出，视为已知量；σ为每千米正常高差的误差，为待估参数；L以千米为单位。

这里的每千米正常高差误差σ，与两地面点的距离相乘，用于表示两点间正常高差的误差；而水准网中的每千米水准高差中误差，用于描述沿水准路线长度累积的水准高差误差。两者有些差别。

将式(2)代入式(1)，则GNSS水准残差高程异常差误差满足

(3)

(4)

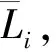
(5)

2.2 似大地水准面成果误差估计算法的性能

(6)

可见，按式(5)评估似大地水准面精度，能有效体现经GNSS水准融合后的实用地面高程异常误差特性，即中长波精度依靠重力地面高程异常控制，短波精度用实测GNSS水准高程异常改善。

或许此时，西王当家人才意识到，一支球队的广告效应的确可能超过对媒体几个亿宣传投入的传播效果，但这种效应与用广告费打出来的效果是不一样的，媒体广告只能说好，球队带来的反响却是利弊相间的双刃剑，有好有坏，甚至坏话比好话更多，负面影响比正面影响更大。

2.3 似大地水准面成果精度评估流程

按上述方法进行似大地水准面成果精度评估的一般计算流程如下：

(1) 设GNSS水准点总数为n，分别将其实测GNSS水准高程异常减去重力地面高程异常，得到n个GNSS水准残差高程异常，进行统计分析。

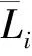
2.4 区域似大地水准面成果的精度表达

本文重点推荐，区域似大地水准面成果的精度评估，用如下两项误差指标和两条误差曲线完整表达：

(2) 误差指标2：实用地面高程异常内部误差Θ。此误差指标可代替当前GNSS水准外部检核方法得到的标准差，两者性质相似。

(3) 误差曲线1：按式(5)计算，以两点间距离L为自变量的实用地面高程异常差误差曲线。

(4) 误差曲线2：按式(2)计算，以两点间距离L为自变量的GNSS水准高程异常差误差曲线。

3 似大地水准面精度评估示例及分析

以某地区似大地水准面成果为例，计算似大地水准面成果的误差指标，绘制误差曲线，评价似大地水准面成果的精度。

计算104个GNSS水准残差高程异常值和5356条边GNSS水准残差高程异常差值，进行统计分析，结果见表1。

表1 GNSS水准残差高程异常(差)

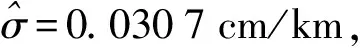
(7)

(8)

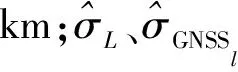
利用上面估计的两项误差指标和给出的算法公式，绘制该区域大地水准面成果的3项误差曲线，如图1所示。由图1可直观地得出以下结论：

(1) 实用地面高程异常差误差(实线)，既不大于重力地面高程异常差误差，也不大于GNSS水准高程异常差误差。实用地面高程异常差的误差曲线总是在其余两个误差曲线的下方。

(2) 在距离L*=105.8 km处，GNSS水准高程异常和重力地面高程异常，对实用地面高程异常的精度贡献相当。小于L*时，GNSS水准高程异常的贡献大，大于L*时，重力地面高程异常的贡献大。

(3) 实用高程异常差误差曲线的斜率，随距离增大而减小，且不大于GNSS水准高程异常差误差曲线的斜率。当斜率接近零时，实用地面高程异常差的误差逼近重力地面高程异常差的误差。

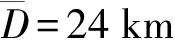
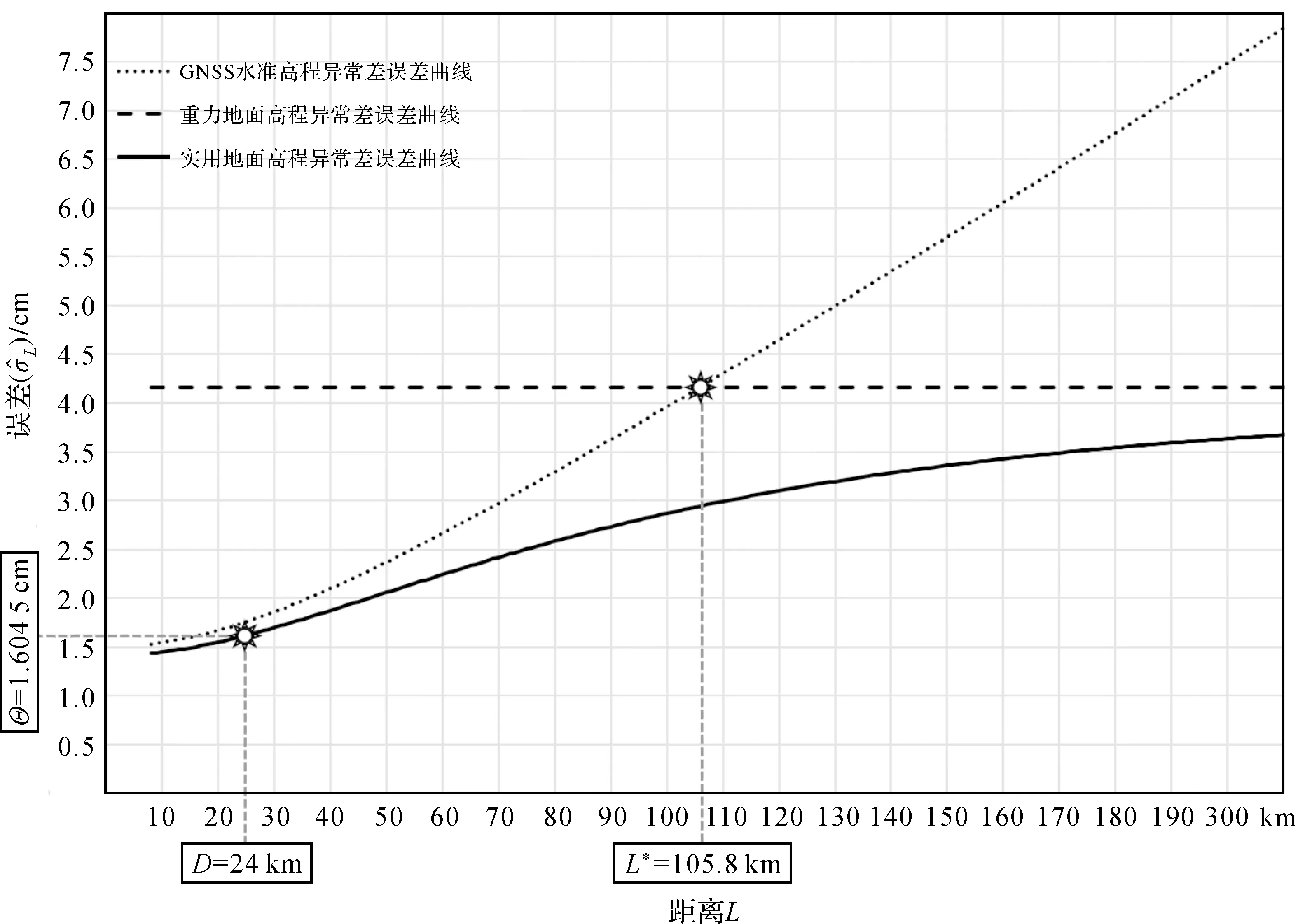
图1 某区域似大地水准面成果的3项误差曲线对比Fig.1 Three kinds of error curves of quasigeoid results

为方便实际应用，可将实用地面高程异常差误差曲线的最大最小值，作为似大地水准面成果的精度范围(1倍标准差)。本例中，最小值1.42 cm(L=10 km)，最大值3.64 cm(L=210 km)，即似大地水准面成果的精度范围 (1倍标准差)为1.42～3.64 cm。

4 结 语

本文基于GNSS水准高程异常与重力场的频域误差特性，研究GNSS水准与重力地面高程异常融合算法的技术要求，采用统计分析技术，提出一种大地水准面成果的误差表达与精度评估方法。经示例测试，得出主要结论如下：

(1) 两点间实用地面高程异常差的误差是其距离的非线性递增函数，区域似大地水准面精度，应采用随距离非线性变化的实用地面高程异常差误差曲线表达。

(2) 实用地面高程异常差的误差，既不大于重力地面高程异常差的误差，也不大于实测GNSS水准高程异常差的误差。

(3) 当两点间距离接近或小于GNSS水准点平均间距时，GNSS水准高程异常对实用地面高程异常的贡献起主要作用。

(4) 较大空间尺度的实用地面高程异常精度，主要依靠重力地面高程异常控制。这说明本文提出的误差表达和估计方法，符合地球重力场性质。

(5) 区域大地水准面成果的精度评估，由本文2.4节给出的两项误差指标和两条误差曲线共4个要素完整表达。