IPSO-BP 神经网络算法在油浸式变压器故障诊断中的应用
宋朝鹏
(武汉市规划研究院,武汉 430000)
0 引言
变压器的运行状态直接影响着电力系统的安全,快速准确地诊断出变压器已有故障或潜伏性故障,对提高电力系统运行稳定性和可靠性具有重要意义。目前,油中溶解气体分析技术(DGA)是对油浸式变压器进行故障诊断最方便、有效的手段之一[1]。
在油中溶解气体分析的应用方面,传统方法主要采用IEC三比值法,该方法为及时发现变压器故障隐患起到了重要作用,但是该方法采用比值编码,存在编码缺损、边界绝对化等问题[2]。针对这些不足,误差反向传播BP(Back Propagation)神经网络被应用到变压器的故障诊断中,并发挥出比较好的效果。但是BP 算法属于梯度下降算法,当样本数目多、输入输出关系复杂时,BP 网络的收敛将非常缓慢,收敛精度不高,甚至出现不收敛的状况。
粒子群优化算法(Particle Swarm Optimization,PSO)是一种近年被广泛研究和应用的群体智能优化算法,具有收敛速度快、全局搜索能力强等优点,采用粒子群算法来优化BP神经网络,可有效克服BP 算法的缺点。然而标准的PSO 算法易陷入局部最优,出现所谓的早熟收敛现象,为此,对PSO算法的相关参数进行改进,并引入变异运算,形成改进的粒子群优化算法,将改进粒子群与BP 算法结合,建立改进粒子群优化BP 神经网络算法(IPSO-BP),以弥补BP 神经网络收敛速度慢、易陷入局部极小值、鲁棒性不好等缺点。将IPSO-BP算法应用于油浸式变压器的故障诊断,测试结果表明,该方法能有效区分变压器的各类故障,显著提高了故障诊断准确率。
1 PSO算法及其改进
1.1 标准PSO算法
粒子群算法是一种基于群体搜索的随机优化算法,起源于1986年Craig Reynolds提出的Bold模型[3]。假定在S维空间中,种群X=(X1,X2,…,XN)中的每一项代表一个粒子,每个粒子有其对应的位置,即待优化问题的一个可能解,该位置用S维向量Xi=(xi1,xi2,…,xis)(i=1,2,…,N)来表示,其移动速度vi=(vi1,vi2,…,vis)。根据目标函数可以计算其适应度,在每次迭代计算中,粒子通过追踪个体最优值Pi(pi1,pi2,…,pis)及全局最优值Pg(pg1,pg2,…,pgs)来调整自己的速度,更新自己的位置,最终达到全局最优。迭代更新公式如下:
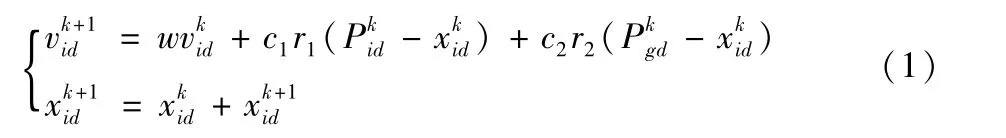
式中:v为粒子当前速度;x为粒子的位置;N为种群规模;k为迭代次数;w为惯性权重;Pi为个体粒子当前最优值;Pg为当前全局极值;c1和c2为加速因子,为非负常数,用以调节粒子向最优位置移动的最大步长;r1和r2为0~1 的随机数。
PSO算法具有较强的全局收敛能力,但是也易出现陷入局部极值、早熟收敛或停滞的现象[4]。为达到更好的优化效果,本文在综合粒子群算法已有优点的基础上,通过改进粒子的参数,引进变异操作,修正粒子个体行动轨迹,从而增强其全局搜索性能。
1.2 PSO算法改进
1.2.1 参数改进
在粒子群算法研究初期,通常将惯性权重设为常数,取得的效果并不佳,后来经过大量研究发现,将惯性权重设置为动态变化的数值后,其搜索效果会明显提高。为了使算法尽快进入局部搜索,本文采用一种改进的非线性递减算法,即在运算早期加快惯性权值的递减速度。设定惯性权值运算公式为:

式中:wmax、wmin分别为最大惯性权值与最小惯性权值;k、K分别为当前的迭代次数和最大允许迭代次数。
在粒子群算法中,加速因子也具有重要作用。加速因子合理配置可加快粒子的寻优速度,减少陷入局部最优的可能性。在运算初期,为确保每个粒子都能较全面地完成局部搜索,可使用较大的c1与较小的c2,而在搜索后期,则适当减小c1、增大c2,加强粒子之间的信息交互,提高收敛的速度。建立加速因子调整公式为:

式中:cmax、cmin分别为设定的参数最大值与最小值;a、b为常数。
1.2.2 引入变异操作
粒子群算法存在易早熟收敛、后期迭代效率偏低等缺点,为弥补这些不足,拓展搜索空间,降低出现局部极值的可能,在算法中引进变异操作。在粒子每次完成更新后,对粒子进行重新初始化,变异操作方式如下:

式中:h为[0,1]内的一个随机数,确定粒子朝最小或最大的方向进行变异;xmax、xmin分别为xij的上界和下界。
2 改进粒子群优化BP神经网络算法
BP神经网络运算可分为两个阶段:第一阶段为正向过程,样本从输入层输入,经隐含层进行逐层计算后得到各单元的输出值;第二阶段为反向传播过程,网络输出误差逐层向前计算出隐含层各单元的误差,并用此误差来修正前层权值与阈值[5]。通过正反向多次运算,直到网络全局误差达到预设精度。由于BP 算法基于梯度下降的原理,不可避免存在易陷入局部最优、收敛速度低及鲁棒性差等缺点[6]。
本文应用改进PSO 算法(IPSO)来训练BP 神经网络,最终搜索出粒子适应度最小时的BP 网络最优权值和阈值。在IPSO优化BP算法时,粒子的维数等于神经网络权值和阈值总个数,在BP 网络中,网络调整权值和阈值是以误差均方值为基准的,因此本文建立了误差均方值与IPSO算法适应度函数的对应关系。IPSO-BP中的适应度函数可表示为:
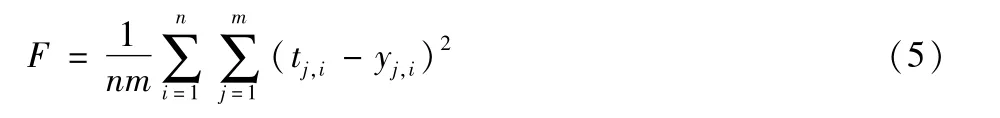
式中:n为训练样本总数;m为输出神经元个数;tj,i为神经元理想输出值;yj,i为神经元实际输出值。
IPSO优化BP神经网络(IPSO-BP)的流程如下。
(1)步骤1:根据输入、输出训练样本集,确定神经网络输入层、隐含层和输出层的节点数,设计神经网络的拓扑结构。
(2)步骤2:初始化算法参数,需初始化的参数有最大迭代次数K,最大速度vmax,群体规模N,惯性权重wmax、wmin,加速因子cmax、cmin,粒子位置xmax、xmin,并将粒子的初始位置及速度初始化为[0,1]的随机数。
(3)步骤3:根据式(5)计算每个粒子的适应度函数值,以此确定每次迭代的Pi与Pg。
(4)步骤4:利用式(1)计算并更新每一个粒子的速度及当前位置。利用式(2)~(3)确定参数的取值,再更新位置,更新后利用式(4)重新对xij进行初始化。重新计算初始化后的每个粒子适应度值,并将其适应度值与其经历过的最好位置Pi作比较,若结果更优,则将Pi作为当前的最好位置。
(5)步骤5:将步骤4 中每个粒子的适应度值与全局所经历的最好位置Pg进行比较,如果当前粒子位置更好,则将当前最好位置赋值给Pg。
(6)步骤6:检验是否符合结束条件(迭代次数达到最大次数或达到最小误差要求),若符合,则停止迭代,输出全局历史最优解,否则转到步骤4。
(7)步骤7:将得到的全局历史最优解映射到BP神经网络的权值和阈值中,得出故障诊断模型。
(8)步骤8:将测试样本输入改进粒子群优化后的BP神经网络中,通过分析输出结果来校验算法性能。
3 IPSO-BP算法在变压器故障诊断中的应用
3.1 网络结构设计
如果油浸式变压器出现放电、过热等内部故障,通常会产生H2、CH4、C2H2、C2H4、C2H6等5 种故障特征气体[7]。本文以这5种气体体积分数作为神经网络的输入量,为避免因训练样本数据的较大差异性而影响神经网络的收敛,需先对数据进行归一化处理。变压器内部故障一般分为5 种故障类型,即高温过热(Y1)、中温过热(Y2)、低温过热(Y3)、高能放电(D1)、低能放电(D2),网络输出可表示为这5 类故障。高温过热、中温过热及低温过热的故障温度分别设定为大于700 ℃、300~700 ℃以及小于300 ℃3种情况。高能放电指较强的火花放电或电弧放电,低能放电指较弱的火花放电或局部放电[8-9]。
在IPSO-BP算法执行过程中,对参数进行合理初始化具有重要影响。通过多次仿真试验,设定最大迭代次数为500,群体规模为50,BP网络拓扑结构为5 -15 -5,粒子维数d=5 ×15 +15 ×5 +15 +5=170,惯性权重最大值wmax及最小值wmin分别设为0.8和0.3,加速因子最大值cmax设为2.5、最小值cmin设为0.5,最大速度vmax=1,常数a、b分别设为0.5、-0.5。本文收集了通过吊芯处理的200组变压器故障数据作为训练样本,输入IPSO -BP 网络进行学习训练,并最终确定神经网络最优的连接权值与阈值。另选用120 组数据作为测试集来测试故障诊断性能。
3.2 变压器故障诊断结果及分析
根据选定的200 组训练样本数据,分别使用BP 算法、PSO-BP算法和IPSO-BP算法对神经网络进行训练学习,训练目标误差精度设为0.000 1。
采用3种算法进行训练时的平均误差随迭代次数k的变化曲线如图1~3所示。从图中可以看出,与BP算法、PSOBP算法相比,IPSO-BP算法在收敛速度、收敛精度、平均收敛性能方面表现更佳。BP算法经过327 次迭代,误差均方根F收敛于0.001 310 8,收敛精度不够理想,收敛速度缓慢,在训练过程中易陷入局部极值,且很难跳出;PSO-BP 算法前期收敛速度较快,后期比较平缓,并逐步陷入局部极小值,最后经过236次迭代达到最优训练值0.000 275 59,收敛精度较好;IPSO-BP算法收敛曲线平滑且收敛精度最高,获得了较好的寻优效果,经过146次迭代收敛于0.000 141 75,有效减小了训练误差。从试验结果还可看出,达到同样的平均误差,采用IPSO-BP算法收敛所需的迭代次数k明显更少,训练效率得到较大提高。由此可见,IPSO-BP算法能够有效避免陷入局部极值,不仅使训练的收敛精度大大提高,其训练的效率也得到明显提升。
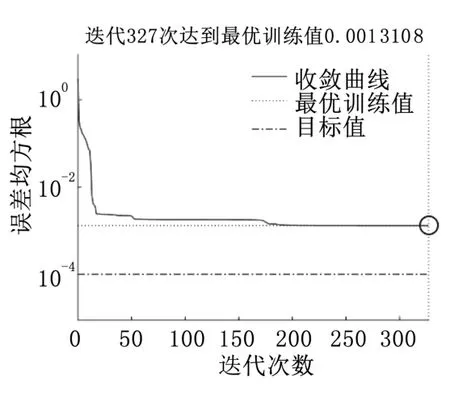
图1 BP算法训练收敛图
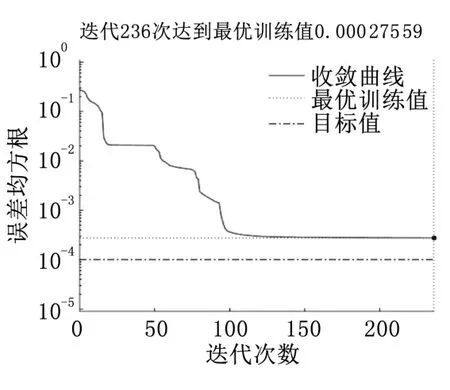
图2 PSO-BP算法训练收敛图
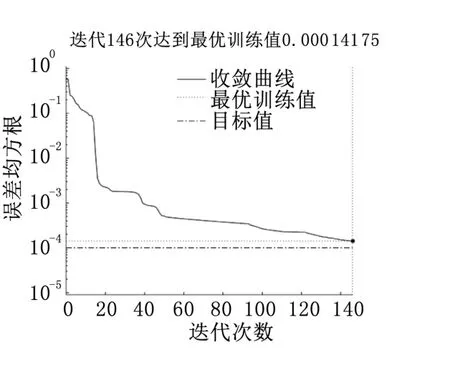
图3 IPSO-BP算法训练收敛图
为了比较不同算法的诊断效果,将收集到的120 组测试数据依次采用BP算法、PSO-BP算法及IPSO-BP算法进行故障诊断。应用3 种算法进行故障诊断的正确率如表1 所示,与BP算法(正确率为79.2%)、PSO-BP 算法(正确率为86.7%)进行比较,本文所采用的IPSO-BP算法(正确率为93.3%)对变压器的故障识别率更高。以上诊断结果表明,IPSO算法在优化神经网络参数过程中具有优越性,表现出较强的泛化能力,可有效地完成故障区分。

表1 诊断准确性对比
为进一步验证本文方法在诊断变压器故障时的实用性,采集5组现场采集的变压器故障实例数据,在进行归一化处理后输入训练好的IPSO-BP神经网络,得出表2 所示的测试诊断结果。诊断结果表明,IPSO-BP算法的故障诊断结果与实际故障类型完全一致,网络诊断准确率高,具有较好的实用性。
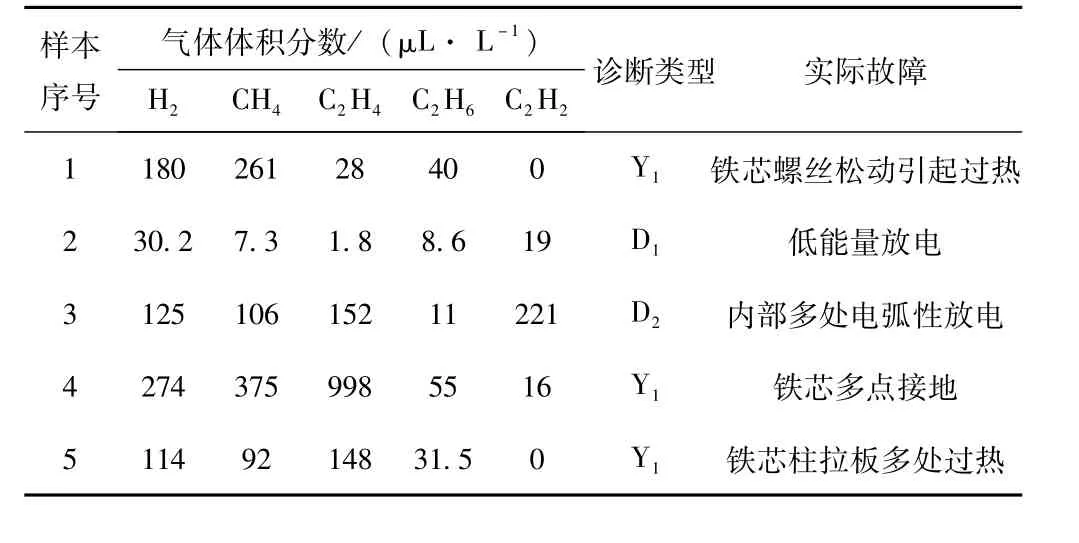
表2 变压器故障诊断实例
4 结束语
针对BP神经网络在油浸式变压器故障诊断应用中存在易陷入局部极值、收敛速度慢等问题,本文提出了一种改进的粒子群优化算法,并将其运用于BP 神经网络的参数优化中。仿真结果表明,本文所采用的IPSO-BP神经网络算法收敛速度快、训练误差小,可有效提高变压器故障诊断的准确率,具有较高的工程实际应用价值。

