一种基于MIMO阵列的高炉雷达三维快速成像算法

闫昱君，敬汉丹，孙厚军，邢光龙,*

(1.燕山大学 信息科学与工程学院，河北 秦皇岛 066004；2.北京理工大学 毫米波与太赫兹技术北京市重点实验室，北京 100081)

0 引言

现代大型高炉属于耗能巨大的“黑箱”设备，操作人员在无法直接观测内部料面的条件下进行复杂布料操作，难以实现对冶炼流程的有效优化。对布料表面的实时监测不仅可以优化冶炼流程，提高冶炼质量，同时可以实现节能减排的目标[1]。

基于激光和超声波的探测方式极易受到高炉内粉尘、温度、气流复杂严酷环境的影响，由于毫米波的穿透特性，毫米波雷达成像技术可以克服粉尘等影响，是当前高炉料面监测的重要技术发展方向。电子科技大学的丁义元于1988年底研制成功了我国第一部监测高炉料面的毫米波雷达，通过反射镜的运动实现对料面的机械扫描[2]；北京科技大学的魏纪东、陈先中等设计了沿高炉料面径向的机械摆动雷达，通过天线的机械摆动实现对料面的扫描[3]。机械扫描雷达结构复杂，在高炉内部复杂环境下，其使用寿命必然大大降低。

近年来，提出了一种新体制雷达——多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达。MIMO雷达采用多个发射天线和多个接收天线，各个发射天线同时发射相互正交的信号，各个接收天线对所有的回波信号进行接收并集中处理[4]。MIMO雷达具有实时性好、分辨能力高、抗干扰能力强等诸多优点，被广泛应用于各个领域。但是，MIMO雷达在高炉料面监测背景下的应用还很有限，已知奥地利的Dominik Zankl等人设计的BLASTDAR雷达已应用于奥钢联钢铁有限公司5#高炉进行料面成像[5-6]；国内北京航空航天大学许鼎[7]和北京科技大学陈先中[8]设计了特种天线单元，设计了T型MIMO成像雷达用于武钢7#高炉。已知的应用皆是对MIMO阵列的天线单元进行设计，而在算法层面上，国内外研究学者并没有提出应用于高炉料面成像场景的针对性成像算法。通过对现有的MIMO雷达成像算法进行研究，发现这些算法应用到高炉料面成像这个大场景下其计算量大、效率低，难以实现对料面的实时成像。

为此，提出了一种基于MIMO阵列的高炉成像雷达距离-角谱域算法。该算法通过对目标的回波信号进行波程近似处理，得到x-y-k域均匀分布的回波数据，对其做收发阵列维快速傅立叶变换和距离维快速傅立叶逆变换，目标在kx-ky-r域实现聚焦，最后通过三维插值将目标图像从kx-ky-r域转换至空间直角坐标系。所提出的算法复杂度低并且利用了运算效率极高的快速傅立叶变换，与已有的MIMO阵列近场成像算法相比，运算效率得到了显著提高。

本文结构安排如下：第1章对所提出的算法进行了理论推导；第2章给出了MIMO阵列的分辨率和阵元间隔的公式；第3章对所提算法进行了仿真验证；第4章对比了所提算法与传统的MIMO阵列近场成像算法的运算量；第5章对比分析了所提算法的成像质量；最后，第6章对全文进行了总结。

1 距离-角谱域算法三维成像原理

1.1 三维成像模型

所采用的阵列形式为L型MIMO阵列，设发射阵元为NT个，沿y轴排列，接收阵元为MR个，沿x轴排列，NT个发射阵元和MR个接收阵元组成了NT×MR的虚拟阵列，成像模型如图1所示。

图1 三维成像几何模型Fig.1 The geometric model of three-dimensional imaging

设第mR个接收阵元的位置为

RRx[mR]=[mRdx,0,0],mR∈[0,MR-1]，

(1)

第nT个发射阵元的位置为

PTy[nT]=[0,nTdy,0],nT∈[0,NT-1]，

(2)

其中，dx和dy表示接收和发射阵元的阵元间隔。设点目标标距坐标原点的距离为R，该点目标与坐标原点的连线与x轴、z轴夹角分别为θ、φ，该点目标在三维空间的位置可以表示为

(3)

1.2 回波波程近似

由式(1)～(3)中各收发阵元和点目标在三维直角坐标系中的位置，可以求出点目标的回波波程为

,

将根号内的二次项展开、化简可以得到

,

将上式按泰勒级数展开，由于目标到天线阵列的距离较远，省略展开后分母中含有R的高次项，可以得到

RRx+RTy≈2R-sinθcosφmRdx-
sinθsinφnTdy

。

(4)

1.3 三维成像处理

采用的信号形式为步进频率信号，设信号起始频率为f0，脉宽为τ，脉冲数(即步数)为N，脉冲间隔(即脉冲重复周期PRT)为T，相邻脉冲的频率阶跃(即步长)为Δf，第n个脉冲载频的初始相位为θn，则该发射信号的时域表达式为

exp{j[2π(f0+nΔf)t+θn]}，

设目标的散射系数为σ，则回波信号为

其中，r为目标散射点到雷达天线的距离。回波信号s0(t)和本振信号混频后，得到视频回波信号

。

式中，假设目标的散射系数σ为1，相位θn-θ0n表示发射信号和本振信号的初始相位差，对于该雷达成像系统，该项应为常数，可假设为零，因此可简写为

(5)

根据式(4)和式(5)可知，在该成像模型下，第(mR,nT)组阵元接收到的回波信号，经过与本振信号混频处理以及回波波程近似后，其回波信号表达式为

(6)

定义空间频率(波数)矢量、空间频率矢量分量以及收发阵元坐标值:

其中，kx和ky可以看作空间频率矢量在x和y方向上的分量，x和y分别代表接收阵元和发射阵元在x轴和y轴上的坐标值，将上述定义的变量代入式(6)可得

s(x,y,k)=exp(-j2kR)·

exp(jksinθcosφx)exp(jksinθsinφy)。

由于发射阵元和接收阵元在x和y平面上是均匀采样，步进频率信号的各个频点在矢量k方向也是均匀的，因此通过对上式进行分析，可以发现上式的回波数据在x-y-k域是均匀分布的，对该回波数据沿发射阵列维和接收阵列维做快速傅立叶变换(FFT)，将回波数据在kx维和ky维压缩至目标点位置：

FFT2D[s(x,y,k)]=

δ(kx-ksinθcosφ,ky-ksinθsinφ)exp(-j2kR)≈

δ(kx-k0sinθcosφ,ky-k0sinθsinφ)exp(-j2kR)，

(7)

式中，k0代表中心频率所对应的波数矢量。经过对回波数据的二维快速傅立叶变换后，在kx-ky二维截面中，数据被压缩至(k0sinθcosφ,k0sinθsinφ)处呈一冲击响应函数δ。以位于(0，0，R)处的目标为例，沿收发阵列维FFT后，其(x，y，k)域和(kx，ky，k)域分布如图2所示。

图2 沿收发阵列维FFTFig.2 FFT along the transceiver array dimension

经过收发阵列维快速傅立叶变换后，得到沿着k方向的一串冲击响应函数，在实际的三维空间中k与kx、ky并不是正交关系，而是在目标与原点之间距离的R方向上，因此通过对快速傅立叶变换之后的回波数据沿距离向进行快速傅立叶逆变换就可以将回波数据压缩至目标点，从而得到目标在kx-ky-r域中的图像：

IFFT1D{FFT2D[s(x,y,k)]}=P(kx,ky,r)≈

δ(kx-k0sinθcosφ,ky-k0sinθsinφ,r-R),

式中，P代表目标点的坐标函数，由此可知通过对回波数据的二维快速傅立叶变换和一维快速傅立叶变换即可得到目标在kx-ky-r域中的坐标，目标的位置由θ、φ、R决定。但是，目标在kx-ky-r域中的图像并不能直观地看出目标点在三维空间直角坐标系中的形状分布和真实位置，因此对处理后的回波数据进行三维插值处理，将其插值到空间直角坐标系：

。

综上所述，对波程近似后的理想回波基带信号做收发阵列维快速傅立叶变换、距离维快速傅立叶逆变换和三维插值即可得到目标点在直角坐标系中的图像。

上述对算法的推导是在回波波程近似后的理想回波模型下进行的，该模型下的回波波程做了相关近似处理，省略掉了分母中含有R的高次项。实际中回波模型的回波波程未做泰勒展开以及相应近似处理，含有分母中与R有关的高次项。在高炉料面这个大成像场景下，天线阵列与料面的距离较远，因此1.2节中省略掉的分母中含有R的高次项的值是非常小的，对目标成像结果的影响可以忽略不计，因此在实际回波模型下，所提出的距离-角谱域成像算法依然可以对目标进行准确的快速三维成像。

距离-角谱域算法的实现流程如图3所示。

图3 距离-角谱域算法流程Fig.3 Flowchart of distance-angle spectral domain algorithm

2 分辨率与阵元间隔

2.1 分辨率

在MIMO阵列成像体制中，距离向的分辨能力取决于发射信号的带宽，方位向和高度向的分辨能力是由MIMO阵列在方位向和高度向进行采样从而实现的。令δz表示成像系统在距离向的分辨率，δx与δy分别表示成像系统在方位向和高度向的分辨率，各方向上分辨率的计算公式为

(8)

其中，c代表光速，B代表步进频率信号的等效带宽，N代表步进频率信号的步数，Δf代表步进频率信号的步长，λc代表步进频率信号中心频率所对应的波长，R代表目标点到阵列平面的垂直距离，LT_x和LT_y是发射阵列分别沿x方向和y方向的阵列孔径宽度，LR_x和LR_y是接收阵列分别沿x方向和y方向的阵列孔径宽度。通过观察上式，得知距离向的分辨率由信号的带宽决定，带宽越大，则在距离向的分辨性能越好；在系统中心频率已定的情况下，方位向的分辨率由阵列在该向的孔径宽度决定，阵列在该向的孔径宽度越大，则其分辨性能越好。

2.2 阵元间隔

MIMO雷达成像性能不仅仅取决于各维度的分辨率，其在很大程度上取决于MIMO阵列的阵元间隔。如果阵元间隔过大，将会导致成像混叠，无法准确地确定目标位置；如果阵元间隔过小，将会增加系统的复杂度，从而使成像所需要的时间以及实际中的系统成本增加。因此，MIMO阵列应该满足一定的阵元间隔条件，使得成像结果在不混叠的前提下最大限度地减少阵元数。下面给出阵元间隔所需要满足的条件。

接收阵元间距dx满足

，

(9)

发射阵元间距dy要满足

，

(10)

其中，目标区域宽度为D，发射阵列孔径宽度为LT，接收阵列孔径宽度为LR，R为目标到MIMO阵列的距离，λmin为信号频带内所对应的最小波长。式(9)和式(10)即为阵元间隔应满足的条件。由此可知，收发阵元间隔与信号波长、目标区域宽度、阵列孔径大小和目标到MIMO阵列的距离有关。

3 仿真结果与分析

采用MATLAB对所提算法在理想回波模型和实际回波模型下分别进行仿真验证。建立点目标，在理想回波模型下对其进行成像仿真，验证理想回波模型下上述算法具有良好的成像性能；对同样的点目标在实际回波模型下对其进行成像仿真并与理想回波模型下的图像做对比，验证实际应用中所提算法的成像性能和运算效率；最后建立料面模型，在实际回波模型下对其进行成像仿真，验证算法的图形重建性能和运算效率。所获得的仿真图像均是通过使用MATLAB 2018a进行仿真得到的。考虑到毫米波对高炉内部粉尘具有良好的穿透效果，选取系统中心频率为77 GHz；考虑到炉内焦炭颗粒尺寸，选取分辨率为0.15 m；考虑到现代高炉料面尺寸，选取成像区域大小为10 m×10 m×4 m。根据上述指标，在图像不混叠的前提下，根据式(17)～(19)可计算得到系统仿真的各项参数如表1所示。

表1 系统仿真参数Tab.1 Parameters of system simulation

3.1 理想回波模型下算法成像仿真

建立3个散射点目标，目标在空间直角坐标系中的位置分别为(-2，2，5)、(0，0，6)、(2，-2，7)。在近似后的理想回波模型下，对3个散射点目标进行成像仿真，验证算法在理想回波模型下的成像性能，目标的成像结果如图4所示。

由图4(a)可以清晰地看出3个散射点目标在空间直角坐标系中的位置图像。由图4(b)、(c)、(d)点目标在各维度的最大值投影图，可以直观地看出在理想回波模型下，所提算法在3个维度均具有良好的目标图像分辨性能和较低的旁瓣水平，验证了第1章对所提算法在理想回波模型下实现的理论推导是正确的。

图4 点目标成像仿真(理想的)Fig.4 The imaging simulation of point target(ideal)

3.2 实际回波模型下算法成像仿真

为了验证距离-角谱域算法在实际回波模型下成像准确性并与理想回波模型下作对比，建立3个与3.1中位置相同的散射点目标。在实际回波模型下，采用所提算法对其进行成像仿真，使用MATLAB中的计时函数，给出距离-角谱域算法在实际回波模型下的算法处理时间，验证该成像算法处理具有较高的运算效率。目标的成像结果如图5所示。

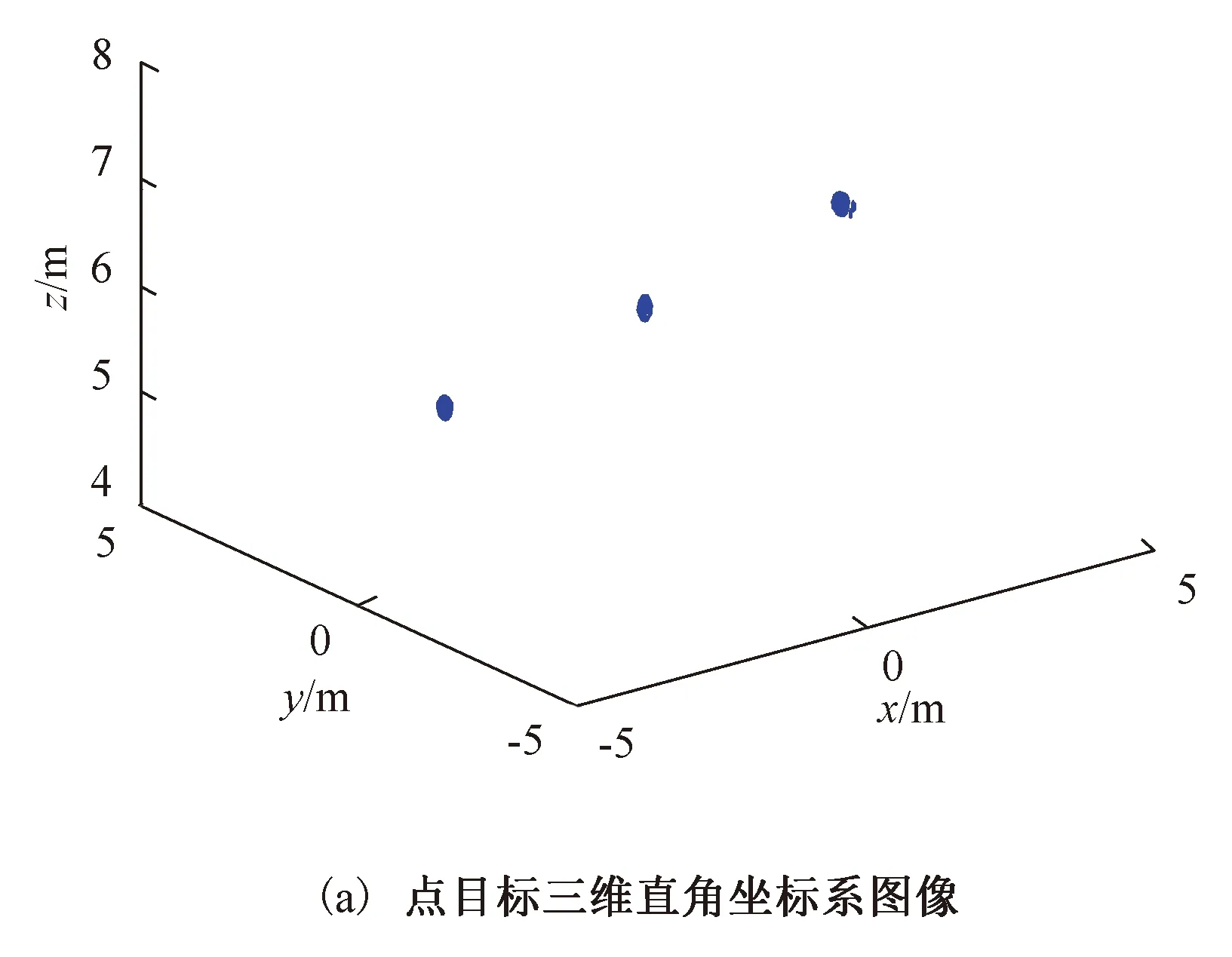
图5 点目标成像仿真(实际的)Fig.5 The imaging simulation of point target(actual)

将图5的仿真结果与图4的仿真结果做比较，发现所提出的距离-角谱域算法在实际回波模型下的成像结果同理想回波模型下的成像结果几乎完全一致，说明在实际回波模型下，所提出的距离-角谱域算法在该大场景下可以准确地对目标点进行成像。通过使用MATLAB中的计时函数，得到该算法对10 m×10 m×4 m的大场景成像所花费的时间约为0.397 s。

为了更加直观地展现该成像算法在实际回波模型下对高炉料面的成像性能和运算效率，在这建立一个高炉料面模型，采用距离-角谱域算法对其仿真成像。通过查阅文献得知高炉炼铁时料线的形状为V型，其料面在三维空间中可近似看成一个锥面。在10 m×10 m×4 m的三维空间中，建立一个料面模型，其在空间直角坐标系中的位置如图6所示。

图6 料面目标三维空间坐标Fig.6 3D coordinate map of the surface target

使用多个散射点目标构建如上图所示的料面目标，对其仿真成像，得到成像结果如图7所示。

由图7可以清晰直观地看到料面目标在三维空间中的形状与位置，与图6所建立的目标模型对比，说明该算法在大场景下对料面具有良好的图像重建性能。通过使用MATLAB中的计时函数，得到使用该算法在10 m×10 m×4 m的空间中对所建立的料面目标模型进行成像处理所需要的时间仅为0.438 s，说明该算法在对料面目标模型进行三维成像时具有较高的运算效率。

图7 料面目标成像仿真Fig.7 The imaging simulation of surface target

4 运算量与分析

为了分析所提出的距离-角谱域算法的运算量并与MIMO雷达反向投影算法(BP算法)[9]和距离徙动算法(wk算法)[10]做比较，首先对BP算法、wk算法和距离-角谱域算法进行逐步分解，分析每一步所需要的浮点运算量，并分别给出3种算法的总运算量，然后计算了具体参数下3种算法的总运算量，直观地看出3种算法的运算量大小，最后定性分析所提算法与其余两种算法相比的优势。

4.1 BP算法、wk算法和所提算法运算量

3种算法大部分的运算量都来自于以下运算：

• FFT和IFFT：长度为N的FFT或IFFT的浮点运算量为5Nlog2(N)[11]。

• 相位相乘：一次复数相位相乘需要6次浮点运算[11]。

• 插值：一次一维线性插值需要4次浮点运算，一次三维线性插值需要28次浮点运算。

根据上述运算开销，分析并给出了3种算法每一步处理所需要的浮点运算量以及总的运算量。设收发阵元数分别为M、N，步进频率信号步数为k。为了便于3种算法运算量的对比，需要对数据量和三维成像空间网格进行统一。对于wk算法，为了使该算法的成像区域扩充到大场景，需要在3个维度上按阵元间隔将回波数据补零至所需成像场景大小。为了便于3种算法运算量的对比，在这里将BP算法的像素点和所提算法的三维插值点均按阵元间隔大小划分，即设BP算法三维像素点数、wk算法补零至所需成像场景后的回波数据点数和距离-角谱域算法的三维插值点数均为x、y、z。

BP算法运算量如表2所示。

表2 BP算法运算量Tab.2 Computation quantity of BP algorithm

wk算法运算量如表3所示。

表3 wk算法运算量Tab.3 Computation quantity of wk algorithm

距离-角谱域算法近似实现运算量如表4所示。

表4 距离-角谱域算法运算量Tab.4 Computation quantity of distance-angle spectral domain algorithm

4.2 具体参数下三种算法总运算量

为了更加直观地看出3种算法的运算量大小，令收发阵元数M和N均为80，步数k为100，x、y、z均为2 000，通过计算可以得知3种算法的总运算量如表5所示。

表5 3种算法总运算量Tab.5 Total computation quantity of three algorithms

由表5可以直观地看出，所提出的距离-角谱域算法的总运算量少于传统的BP算法和wk算法的总运算量。

4.3 算法运算量对比与分析

MIMO雷达BP算法是在时域上对每个像素点进行相干叠加，逐个像素点聚焦的串行处理方式导致BP算法的运算效率非常低。MIMO雷达wk算法是在波数域上对雷达回波数据进行相应成像处理，虽然使用了运算效率高的FFT和IFFT处理，但是其弊端在于在大场景下为了扩充成像区域，必须将雷达的回波数据按阵元间隔来补零至所需成像场景大小，这样将导致最后的成像像素点数过多，存在大量的冗余。

所提出的距离-角谱域算法中的插值点是按阵元间隔大小来划分的，这是为了与wk算法的运算量做对比，而在实际应用中，无须按照阵元间隔大小来划分插值点，只需要将插值点间隔设为分辨率大小即可使图像具有良好的性能，因此所提出的距离-角谱域算法在实际应用中其运算量远远小于BP算法和wk算法。

5 成像质量与分析

BP算法是最标准的用于成像质量对比的算法，其成像精度高，常用于阵列成像质量的标准化分析；wk算法在波数域插值时存在近似，有误差，因此不适合用来做标准化分析。为了验证所提出的算法具有良好的成像质量，在实际回波模型下将其与BP算法的成像质量进行对比与分析。

为了避免多个点目标之间的相互影响，采用单个点目标，对目标位于成像区域中心处和边缘处两种情况，使用所提出的算法和BP算法在表1的系统仿真参数下对点目标进行成像仿真，对比分析两种情况下算法的成像精度和旁瓣水平。

5.1 目标位于成像区域中心处成像质量

在成像区域中心处建立单个点目标，其在直角坐标系中的位置为(0，0，6)，使用所提出的算法对其进行成像，各维度成像结果如图8所示。

在成像区域中心处，建立同样的单个散射点目标，在相同的仿真参数下，使用BP算法对其进行成像仿真，得到各个维度的成像仿真结果如图9所示。

由图8和图9，可知两种算法在成像区域中心处各维度的成像误差和旁瓣水平，如表6所示。

表6 成像质量对比(中心)Tab.6 Comparison of imaging quality(center)

由表6可知，在成像区域中心处，所提出的算法和BP算法在各维度的成像精度都非常高，误差为0；在旁瓣水平上，所提出的算法在x维和y维略高于BP算法，在z维略低于BP算法。

5.2 目标位于成像区域边缘处成像质量

在成像区域边缘处建立单个点目标，其在直角坐标系中的位置为(3，3，7)，使用所提出的算法对其进行成像，各维度成像结果如图10所示。

使用BP算法对其进行成像仿真，得到3个维度的成像结果如图11所示。

由图10和图11，可以直观清晰地看出两种算法在成像区域边缘处对目标成像时，各个维度的成像误差和旁瓣水平，对比如表7所示。

表7 成像质量对比(边缘)Tab.7 Comparison of imaging quality(edge)

由表7可以直观地看出，当目标在成像区域边缘处时，所提出的距离-角谱域算法和BP算法在3个维度的成像精度都非常高，误差为0；在旁瓣水平上，所提出的距离-角谱域算法在3个维度上略高于BP算法。

综上所述，所提出的距离-角谱域算法在该成像场景下具有良好的成像质量。

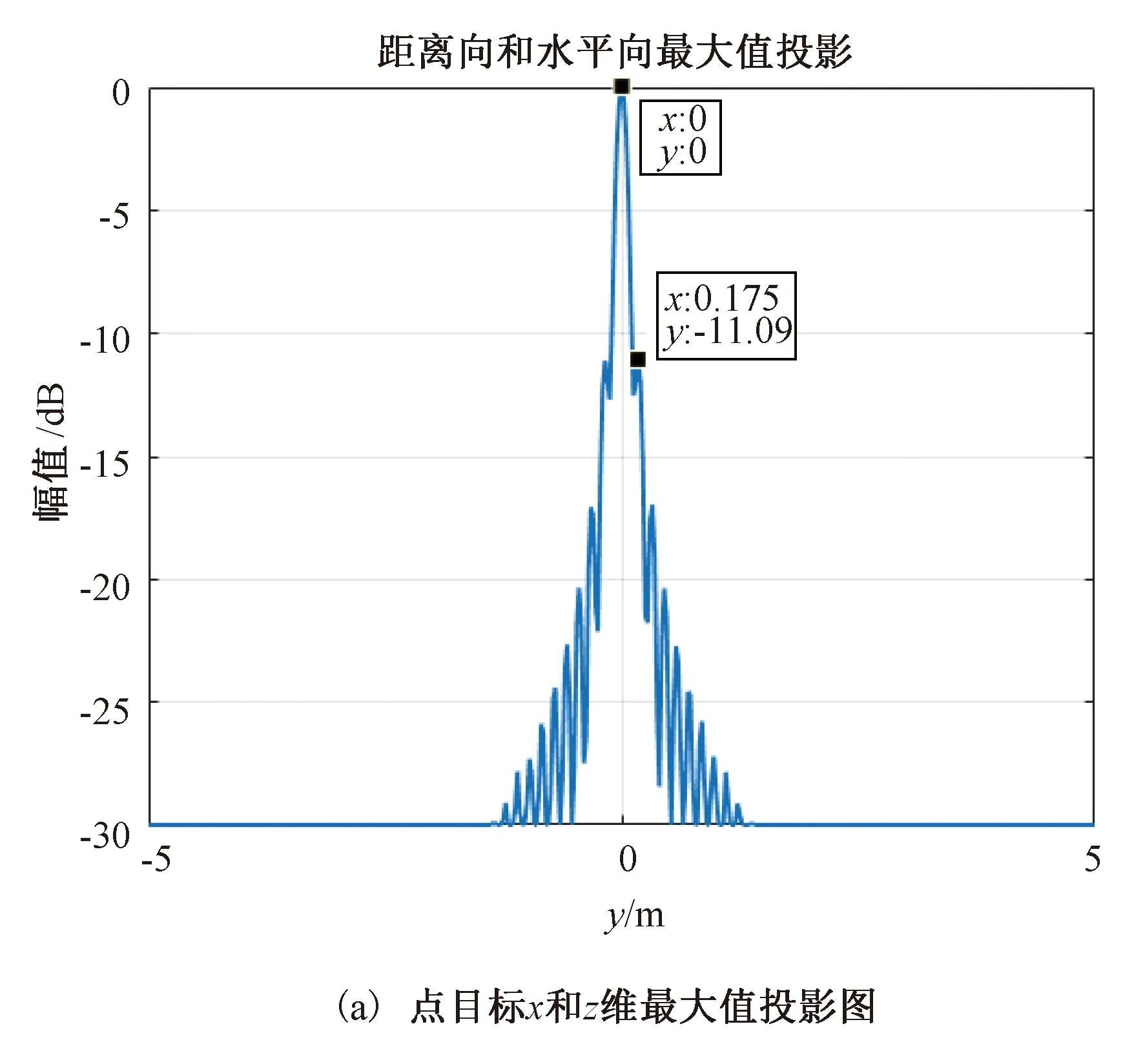
图8 距离-角谱域算法各维度成像仿真(中心)Fig.8 The imaging simulation of distance-angle spectraldomain algorithm in all dimensions(center)

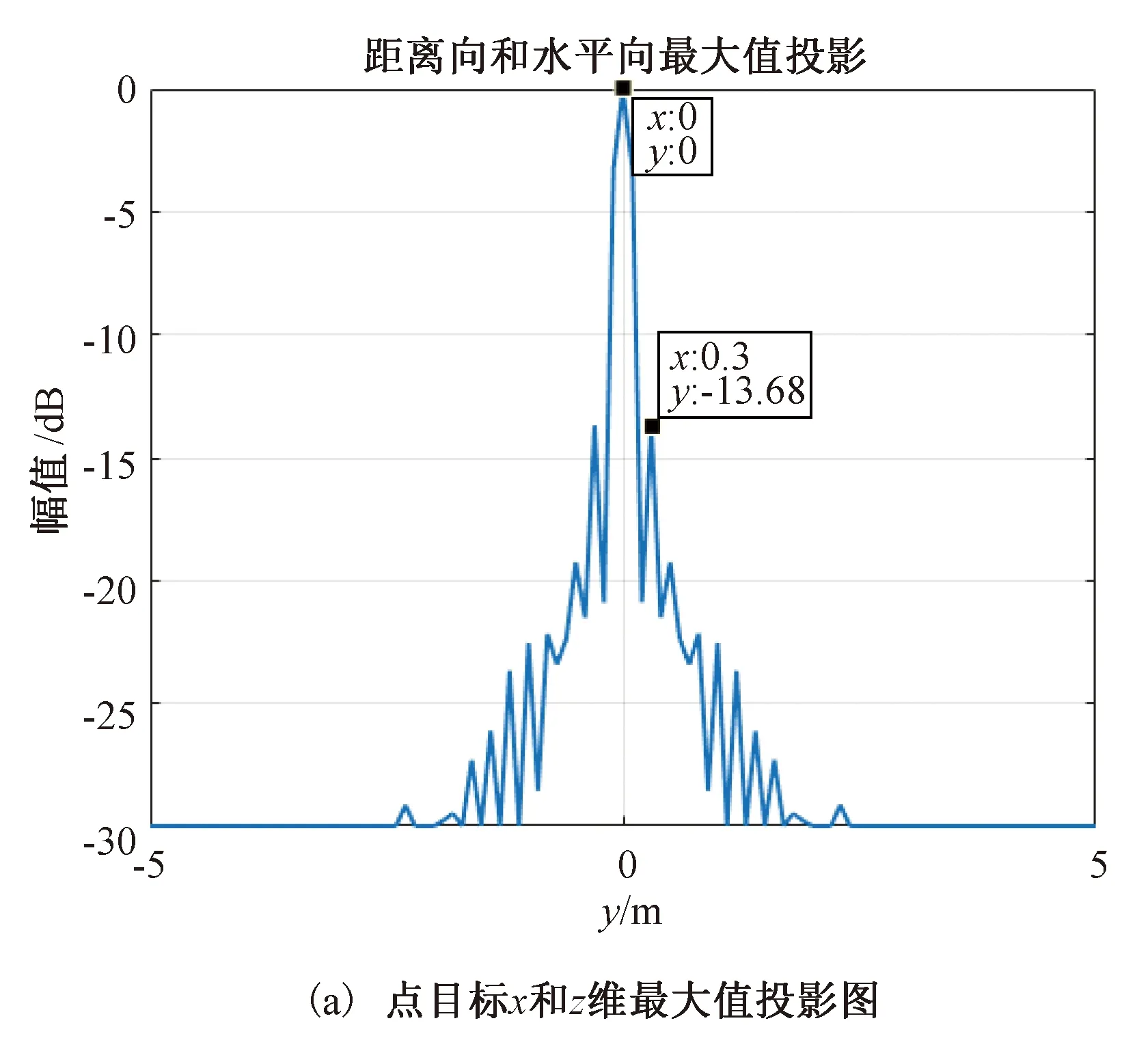
图9 BP算法各维度成像仿真(中心)Fig.9 The imaging simulation of BP algorithm in all dimensions(center)

图10 距离-角谱域算法各维度成像仿真(边缘)Fig.10 The imaging simulation of distance-angle spectraldomain algorithm in all dimensions(edge)

图11 BP算法各维度成像仿真(边缘)Fig.11 The imaging simulation of BP algorithm inall dimensions(edge)

6 结论

本文提出了一种基于MIMO阵列的大场景快速成像算法——距离-角谱域算法。对该算法在理想回波模型和实际回波模型下分别进行成像仿真，验证了该算法在保证了成像性能的前提下具有较高的运算效率。文中还对比分析了距离-角谱域算法与已有的MIMO阵列近场成像算法的运算量和成像质量，体现了所提算法的高运算效率和良好的成像质量。下一步将开展MIMO阵列近场毫米波成像系统的工程化研究工作，实现所提算法的工程化应用，对算法进行进一步的验证和改进。