基于MSMA可逆特性的自感知执行器结构优化设计
鲁军,常强,李园君
(沈阳理工大学自动化与电气工程学院,沈阳110159)
0 引言
1996年,美国的K.Ullakko博士[1]发表了一篇名为“磁控形状记忆合金:一种新型的执行材料”的文章,MSMA才得到国内外学者的关注。芬兰的AdaptaMat公司生产的MSMA元件推动了该磁性功能材料的发展。由于磁控形状记忆合金(MSMA)发现较晚,因此国内外对MSMA的研究成果还不是很多。美国马里兰大学的Ronald N.Couch教授[2-3]在对MSMA的静态工作特征的研究基础上,对材料的动态工作特征进行了深入的研究。为新型MSMA装置的研制提供了大量宝贵经验。
在MSMA材料正逆特性的研究上,国内也有多所学校对其进行了研究。北京航空航天大学的蒋成保、徐惠彬等人[4]基于国内外对磁控形状记忆合金材料的研究成果,在MSMA材料的制备方面有了突破性进展。制备的MSMA材料形变大、响应速度快,具有良好的传感特性。沈阳工业大学的王凤翔教授等[5-7]对MS⁃MA执行器、MSMA振动能量采集器、MSMA振动发电机进行了深入的研究,并取得了一定的研究成果。沈阳理工大学[8-10]对MSMA传感器和MSMA执行器做了大量研究,设计了MSMA传感器样机,并结合实验对MSMA材料的正、逆特性进行了研究。
根据以上研究结果表明,国内外对MSMA自感知执行器的研究还很少。因此,基于以上研究成果,研制基于MSMA自感知执行器对MSMA具有重要的意义。本文基于MSMA传感器和MSMA执行器的研究,设计出MSMA自感知执行器,并对其结构进行优化。
1 MSMA自感知执行器磁路数学模型
MSMA自感知执行器的等效磁路模型[11]如图1所示。MSMA自感知执行器的等效磁路模型的总磁动势为Fa=NIa,R1和R2是单个永磁体的磁阻,R3是气隙处的磁阻,N是线圈的匝数,Ia是励磁电流,Φ0是磁路中的总磁通,Φ1和Φ2分别是通过铁心上下两部分磁路的磁通,且Φ0=Φ1+Φ2。
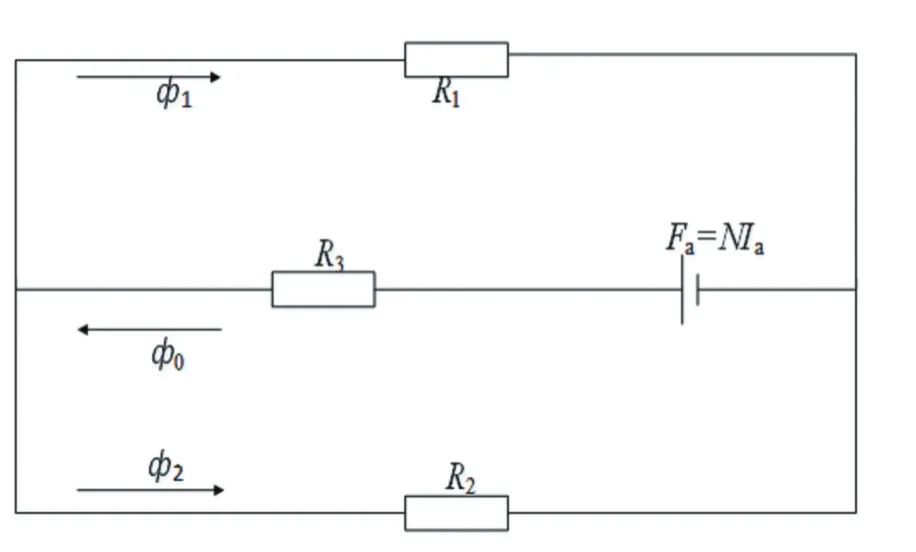
图1 MSMA自感知执行器等效磁路模型
由磁路欧姆定律可得,励磁线圈产生的磁通量Φ的表达式为:

式中,Φ——磁路中的磁通量,单位Wb;
F——励磁线圈的磁动势,单位A;
Rm——铁心磁路中的总磁阻,单位A/Wb。
总磁阻Rm表示为:

磁路中各部分磁阻的计算公式为:

式中,R——磁路中的磁阻,单位A/Wb或H-1;
l——磁路材料的导磁长度,单位m;
μ0——真空磁导率,4π×10-7H/m;
μr——磁路材料相对磁导率;
A——磁路材料的导磁面积,单位m2。
励磁线圈产生的磁通量为Φ,由磁通量定义公式得到相应的磁通密度Bc计算公式为:

式中S为磁路中气隙截面积,与MSMA材料截面积相同。
磁通密度Bc和磁场强度Hc的关系为:

由上述内容可以得到励磁线圈在气隙处产生磁场强度Hc的计算公式为:

2 MSMA自感知执行器结构设计
2.1 励磁方式的选择
自感知执行器的励磁方式可以分为三种励磁方式:永磁体单独励磁、励磁线圈单独励磁、永磁体和励磁线圈共同励磁。本文采用的是永磁体和励磁线圈共同励磁方式。由于永磁体自身可以提供一定的磁感应强度,通过调节励磁电流的大小和方向可以增大或减小MSMA材料所处的磁感应强度。若采用永磁体单独励磁,则磁感应强度大小无法调节,不适用于自感知执行器实验研究;当励磁线圈单独励磁时,则必须通过足够大的电流才能使MSMA材料产生形变,若电流过大,磁阻不变的情况下,会增加励磁功率,故采用永磁体和励磁线圈共同励磁方式,可调节磁感应强度并减小励磁功率。
2.2 永磁体材料的选择
目前,常用的永磁体材料有铁氧体、铁钴钼和钕铁硼等,相对于其余两种材料,钕铁硼的磁性能更具优势,它的磁能积很大,单位体积的材料能够提供较强的磁场,自感知执行器的整个磁路磁阻会变小,整个磁路的励磁功率也会减小。虽然钕铁硼的剩磁越大越好,但经过有限元软件分析得到剩磁大的钕铁硼材料体积过小,不易加工。综合考虑本文使用的钕铁硼牌号为N45。材料剩磁为1.32T~1.48T,矫顽力为923KA/m,最大磁能积为 342kJ/m3~366kJ/m3。
2.3 铁心材料的选择
铁心材料是磁路上不可缺少的组成部分,所以选择合适的材料可以减少磁阻,在磁路中建立均匀的磁场。表1给出各类材料的性能参数。

表1 材料特性表
铁镍合金,主要成分是铁、镍,有时还添加有钼、铬等元素。当磁场较弱时,该合金同样有较高的磁导率和较低的矫顽力。硅钢片它是一种含碳极低的硅铁软磁合金,一般含硅量为0.5~4.5%。加入硅可提高铁的电阻率和最大磁导率,降低矫顽力、铁芯损耗(铁损)和磁时效[12]。由于硅钢片的性能参数比铁镍合金的要好很多且价格低廉,所以铁心材料选择的是硅钢片。
2.4 励磁线圈几何参数的确定
为了准确确定励磁线圈的几何参数,需要明确励磁线圈的磁场强度。磁场强度可通过MSMA的性能参数确定,励磁线圈由直流电励磁,选择合适的漆包线线径对通入电流以及线圈缠绕体积都起着决定作用。而励磁线圈的厚度则可通过线圈骨架进行确定。
本线圈骨架是订制的,长宽高分别为38mm、16.5mm、25mm,线圈一层可缠绕的公式为:

式中kη为排绕系数。
线圈单位厚度上的层数公式为:

式中kβ为叠绕系数。
线圈的厚度为:

线圈的总匝数为:

其中,H 为场强,Lc为线圈长度。将(7)、(8)、(9)代入(10),得到励磁线圈总匝数。若MSMA的材料伸长率高于3%,则励磁线圈提供的磁场也相应增加,在一定的范围内,增加线圈的匝数可以提高感应电压的大小。因此,根据励磁线圈的实际计算结果及其在An⁃soft Maxwell上的仿真结果,计算其总匝数为1200匝。
在正常通电的情况下,其允许通入的最大电流密度的范围为J=2~5A/mm2,由于MSMA自感知执行器的励磁线圈不是一直工作的,只有在实时消振过程中才会通入励磁电流,因此在这里可以将电流密度J选取为4A/mm2,由此漆包线的线径可通过电流密度来进行计算,公式如下:

式中,I——励磁线圈通入电流,单位为A;
J——励磁线圈中的电流密度,单位为A/mm2;
D——线圈缠绕漆包线的直径,单位为mm。
根据式(11),取 J=4A/mm2,电流 0.8A,可以算出励磁线圈线径D=0.51mm。
由于MSMA材料在偏置磁场为0.25T~0.6T的范围内,其产生的形变量的变化与磁感应强度的变化基本呈线性关系,所以让永磁体提供0.25T的磁场,励磁线圈提供0.35T的磁场。
通过导线的电阻率可计算出线圈的总电阻,公式如下:

其中,Sd代表导线的有效截面积,ρ代表铜的电阻率;d为代表裸线直径。
经计算得出电阻R为10.3Ω,励磁电流为0.8A,根据P=I2×R,计算得出励磁线圈的功率为6.5W。
通过MSMA传感器的相关研究可知,MSMA自感知执行器在传感过程所产生的感应信号非常小,而传感线圈输出的电压信号与其匝数有着密不可分的关系,匝数越多感应电压越大。因此为在有限的空间内可以缠绕更多匝的线圈,传感线圈使用0.35mm的漆包线,匝数为2000匝。
2.5 气隙尺寸的确定
随着气隙的增大,其漏磁也会随之增大导致气隙的磁阻增大。选择合适的气隙可以减小励磁功率。根据磁路欧姆定律:
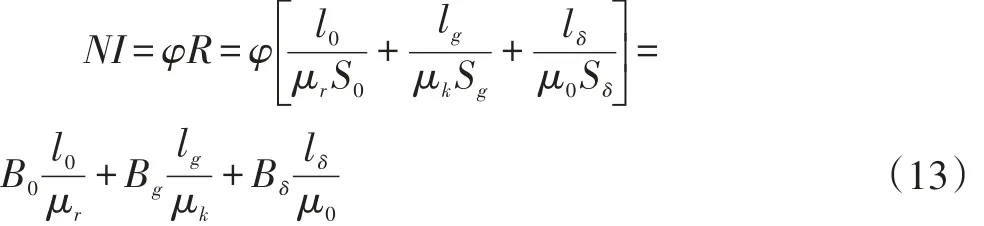
根据上式(13)可知,铁心的磁导率远大于气隙的磁导率,故可以忽略铁心的部分。因此,在安匝数不变的情况下,随着B的增大,气隙处的磁感应强度会随之减小。由于实验材料MSMA的尺寸大小是2.5mm×5mm×25mm,其长度为2.5mm,考虑到实验过程中给材料的激振力,为保护材料不受损坏以及有空间放置特斯拉计,则需要在气隙中间放置1mm的U型护套。因此气隙的尺寸长度最小定为3.5mm。
3 MSMA自感知执行器的有限元分析
有限元分析[13]是将复杂的问题简单化,由于自感知执行器是一个非线性的系统,所以需要有限元分析来模拟一些环境变量,进而达到优化自感知执行器的目的[14]。
3.1 自感知执行器优化前3D 仿真模型
自感知执行器优化前的3D模型图如图2所示。气隙宽度为4.5mm,永磁体宽度为2mm,励磁线圈匝数为1700匝。

图2 自感知执行器优化前3D模型图
在Ansoft Maxwell软件中对其进行电磁仿真可得知:当永磁体单独励磁时,通过气隙的磁通密度约为260mT,如图3所示。当永磁体和励磁线圈共同励磁时,通过气隙的磁通密度为610mT,如图4所示。

图3 永磁体单独励磁时磁通密度曲线图
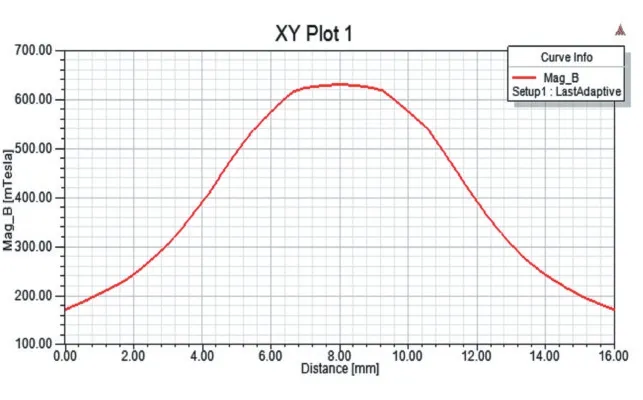
图4 永磁体和励磁线圈共同励磁时磁通密度曲线图
3.2 自感知执行器优化后3D模型
经过理论计算和对自感知执行器的各部分结构的优化设计,自感知执行器优化后的3D模型图如图5所示。

图5 自感知执行器优化后3D模型图
由图5可知,此模型为自感知优化后的3D模型图,气隙宽度为3.5mm,永磁体宽度为1.3mm,励磁线圈匝数为1200匝。在Ansoft Maxwell软件中对其进行电磁仿真可得知:当单独永磁体励磁时,通过气隙的磁通密度约为260mT,如图6所示。当永磁体和励磁线圈共同励磁时,通过气隙的磁通密度为625mT。如图7所示。

图6 优化后永磁体单独励磁时磁通密度曲线图

图7 优化后永磁体和励磁线圈共同励磁时磁通密度曲线图
3.3 模型优化前后对比
由仿真之后的磁通密度曲线图可知,自感知执行器前后对比效果明显,优化后的仿真结果:在匝数为1200匝时,励磁线圈提供的磁通密度较优化前的磁通密度增加了15mT。由以上结果可知,本文使用了较少匝数的励磁线圈也可以提供较强的磁通密度,这样可以减少磁路的总磁阻,进而减小励磁功率,达到了优化的目的。
4 结语
本文对MSMA自感知执行器的励磁方式、铁心材料、励磁线圈、气隙尺寸等进行了设计,并对设计之后的模型进行了有限元仿真分析,与优化前的模型进行了对比,优化后的MSMA自感知执行器中的磁通密度增大了15mT,磁路中的励磁功率减小了30%,达到了优化MSMA自感知执行器的目的。为以后设计MSMA自感知执行器提供了一个新的思路。

