基于趋势预测的关键链自适应缓冲监控策略

张俊光 杨珮祯

摘 要：经典缓冲监控方法忽略了单个活动的缓冲消耗信息，没有结合项目实际执行情况进行监控强度的调整，无法有效提升项目进度的管理绩效。基于此，本文在缓冲分配的基础上引入活动缓冲消耗的位置信息和速率信息，对后续活动的监控强度进行调整，提出了基于趋势预测的关键链自适应缓冲监控策略。仿真结果表明，本文的缓冲监控方法在保证项目按时完工的前提下，大大减少了红色预警的频次，并且在项目成本方面明显优于传统的缓冲监控方法，有效地降低了不必要的资源浪费。

关键词：关键链;缓冲监控;缓冲分配;缓冲消耗速率;预测

中图分类号：F062.4文献标识码：A文章编号：1003-5192（2021）01-0084-06doi：10.11847/fj.40.1.84

Abstract：The classical buffering monitoring method ignores the buffering consumption information of a single activity and fails to adjust the monitoring intensity according to the actual implementation of the project， so it cannot effectively improve the management performance of the project schedule. Based on this， the proposed method introduces the location information and velocity information of active buffer consumption on the basis of buffer allocation， adjusts the monitoring intensity of subsequent activities， and proposes a critical chain adaptive buffer monitoring strategy based on trend prediction. The simulation results show that the buffer monitoring method in this paper greatly reduces the frequency of red warning， and is superior to the traditional buffer monitoring method in terms of project cost， effectively reducing unnecessary resource waste.

Key words：critical chain; buffer monitoring; buffer allocation; buffer consumption rate; prediction

1 引言

1997年，Goldratt[1]將约束理论应用到了项目管理领域，提出关键链项目管理理论（critical chain project management， CCPM），从资源和工序的逻辑关系出发，找到了制约项目进度的关键链，并通过提取活动安全时间，进行尾部集中形成缓冲来实现对项目的风险共担，使得工期缩短并且按时完工率得到了提高。如何对缓冲进行有效管理是CCPM研究的核心问题，包括缓冲确定[2～6]和缓冲监控两大领域，缓冲监控通过分析缓冲的消耗情况来确定项目实际进展与计划进度间的偏差，判断项目延迟的可能性，从而决定下一步需要采取的措施，并对基准计划进行校正和修复，是确保项目按时完工的重要手段[7]。

在Goldratt将缓冲均分为三部分（绿区、黄区和红区）进行静态监控的基础上，学者们将静态监控基准点改进为递增的、变化的等多种设置方式，对监控方法进行改进。Goldratt的静态缓冲监控方法将缓冲等分为绿色、黄色、红色三个区域[1]，分别代表项目执行情况良好、加强项目监控、立即进行赶工。该方法的不足之处在于没有考虑链路的完工比例，且在项目后期会由于缓冲剩余量较少的信息而发出不必要的预警。针对静态三分法的不足，Leach[8]提出了相对缓冲监控法，两个监控触发点的设置随链路完工比例的增加而升高，这一设置考虑了项目不确定性随项目进展降低的特点，减少了错误预警信息的情况。之后，Kuo等[9]，Bevilacqua等[10]提出依据项目阶段确定缓冲大小并进行监控。Gonzalez等[11]提出对缓冲监控参照量进行阶段划分和监控，但这些方法依然是静态的，难以适应项目复杂的动态环境。基于此，别黎和崔南方[12]通过动态计算缓冲大小、设置监控点来监控项目实际进度与计划之间的差异，但该方法是基于项目层面的监控。之后，别黎等[13]在该方法基础上引入活动敏感性信息，实现了活动层面的监控。此外，徐小峰等[14]结合挣值分析和贝叶斯估计方法，研究了关键链资源计划的进度偏差预警功能。Martens和Vanhoucke[15]进一步完善了基于挣值管理的缓冲区监控方法。刘志清等[16]基于完工概率修正了关键链法，更好地处理资源约束和进度偏离情况下的项目进度优化。淦未宇和仲伟周[17]提出一种新的前瞻性项目控制方法，避免了由于项目的一次性带来的预测失效问题。Zhang等[18]，宋喜伟[19]将监控与预测相结合，应用灰色模型、马尔科夫链预测后期活动的进度情况从而减少不必要的紧急赶工。张俊光和万丹[20]提出一种实时滚动的动态缓冲监控方法，研究了缓冲监控剩余量的再分配。郭海燕[21]建立了成本、进度、质量三要素的关键链缓冲区动态管理模型。胡雪君等[22]在缓冲监控中引入统计过程控制方法，实现了活动层面和项目层面不确定性信息的集成。

综上所述，现有的缓冲监控方法虽然考虑了项目执行中不确定性的变化，但本质上仍是在项目计划阶段对缓冲监控进行的提前规划，不能结合项目实际执行中的情况进行监控强度的调整。因此，本文将活动的缓冲消耗位置信息和速率信息纳入监控过程中，从定性与定量相结合的角度设计监控基准点的调整，提高缓冲监控绩效。本文的创新之处有以下两点：第一，将活动缓冲消耗穿透红色缓冲线的次数和缓冲是否有余量这两种缓冲位置信息纳入活动执行情况分类标准，并据此对项目后续趋势进行定性预测。第二，考虑活动层面的缓冲消耗信息，基于活动缓冲消耗速率信息对基准点调整进行了量化调整，实现了项目缓冲的持续动态监控。

2 基于趋势预测的自适应缓冲控制模型

本文将以活动为单位进行监控，结合活动关联度指数CRI对项目缓冲进行分配后，根据项目活动的实际执行情况实时调整缓冲监控基准点，并对基准点调整规则进行量化处理，通过对缓冲的有效监控实现项目的顺利执行。

2.1 基于CRI的项目缓冲分配

缓冲监控的前提是对项目缓冲进行分配，将尾部集中的緩冲基于项目活动的划分进行分散式管理，这样有利于对缓冲进行更精准的监控。CRI反映了各项活动的不确定性对项目工期不确定性的影响程度[23，24]，能够体现活动的不确定性，因此在缓冲分配体系中可以引入CRI指标。

不同活动CRI值的大小衡量了各个活动对项目工期的影响程度，分配到各个活动的缓冲大小根据活动CRI水平而定。具体地，活动CRI指标越高，意味着该活动对整个项目工期不确定的影响更大，此时应该设置较大的缓冲分配量，用更多的缓冲来分担工期风险;反之，若活动CRI值较低，说明该活动对项目的影响较小，分配较少缓冲即可。依据活动CRI对项目缓冲进行分配，能够有效保证项目的顺利实施，减少过多的计划调整带来的项目工期不稳定及成本费用。

活动CRI的大小可以通过蒙特卡洛模拟方法得出，计算过程如（1）式所示[23]。

2.2 项目紧急赶工工期设置

依据活动CRI进行缓冲分配之后，参照Goldratt[1]提出的静态缓冲监控方法，将各活动分配到的缓冲等分为绿黄红三部分，即设置项目各活动的初始黄色基准点为33%，初始红色基准点为67%。当缓冲消耗比例低于黄色基准点时（即处于绿色区域），无需采取行动;当缓冲消耗比例在黄色基准点与红色基准点之间时（即处于黄色区域时），表明项目需要加强监控，并制定可能采取的计划;当缓冲消耗比例达到红色基准点时（即处于红色区域），表明项目很有可能超期，需要立即进行紧急赶工，以应对项目延期。

设项目关键链上共有n项活动，活动i（i=1，2，3，…，n）的黄色基准点为By（i），红色基准点为Br（i）。若活动i（i=1，2，3，…，n）需要紧急赶工，本文设定紧急赶工工期的计算方式如下

活动最大可赶工时间ri是在满足活动固有特性的基础上，通过增加人力物力所能达到的最大赶工效果。举个简单例子，1个工人粉刷1间教室的估计工期是4天，其中包括3天的粉刷时间和1天的干燥时间，当我们限制工人的最高数量为3时，该活动的最大可赶工时间是2天，这是由于1天的干燥时间是无法进行压缩的。需赶工活动的最大可赶工时间可设置为该活动计划工期与CRI的乘积[14]，如（7）式所示

2.3 缓冲监控基准点调整

对于关键链项目而言，缓冲是各活动之间连接的纽带，根据项目所处环境制定的缓冲监控策略直接决定了项目整体系统的强度。在完成缓冲监控策略的前期参数设置后，项目绿、黄、红三个缓冲区域的划分直接决定了监控行为的具体实施，是缓冲监控策略中最重要的环节，因此设置合理的黄色基准点和红色基准点是提高项目运作效果和有效管理缓冲的基本保证。在保证项目按时完工以及降低项目监控成本的双重目标下，本文设定监控基准点调整规则如下：

2.3.1 不调整规则

（1）未穿透：在项目执行期间，若关键链上的活动缓冲消耗一直未能越过红色基准点，这表明项目进展问题不大，按此趋势进行下去，项目能够在计划时间内完工，延误概率较小，此时无需对两个缓冲监控基准点进行调整，也无需进行紧急赶工。如图1（a）所示。

（2）穿透一次红色缓冲线且还有缓冲余量：若活动缓冲消耗越过了红色基准点，但此时活动缓冲仍有余量，这表明活动很可能会发生延误，此时应立即启动紧急赶工程序，调配人力物力对该活动采取赶工措施。但此时无需进行监控基准点的调整，这是因为缓冲仍有余量的情况代表了项目有一定概率能够按时完工，此时没有必要调整项目监控强度。如图1（b）所示。

2.3.2 红色缓冲线调整规则

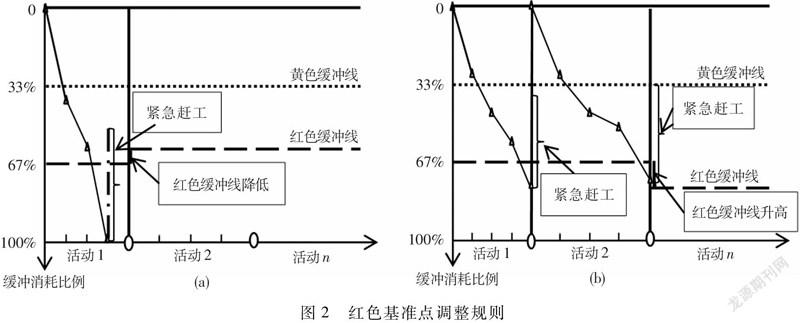
（1）穿透一次红色缓冲线且无缓冲：项目执行中，若活动缓冲消耗第一次越过红色基准点时就出现了活动缓冲消耗殆尽的情况，即该活动缓冲消耗比例超过100%，这说明项目的红色基准点设置过低，未能提前检测到该预警情况，此时应立即进行紧急赶工，同时降低其后活动的红色缓冲监控基准点，加大监控强度。如图2（a）所示。

由图2（a）可以看出，缓冲消耗记录线的斜率反映了活动缓冲消耗的快慢，记录线越陡，斜率越大，说明该活动的缓冲消耗越快，按时完工概率越低，此时应将加大后一活动的监控强度，即红色缓冲线设置越低，此时红色基准点的调整规则如（8）式所示。

（2）穿透两次红色缓冲线且都有缓冲：若活动执行中连续两次出现活动缓冲消耗越过红色基准点但缓冲都有余量的情况，这说明此时项目仍在按计划进行，红色监控基准点设置过高引起的持续赶工是不必要的，浪费了资源。此时应调高项目的红色基准点，如图2（b）所示，调整规则如下。

2.3.3 黄色缓冲线调整规则

若活动执行中连续两次出现活动缓冲消耗越过红色基准点同时缓冲消耗比例都大于100%的情况，这代表可能是项目前期的缓冲分配或者活动工期预估中出现了较大问题，这种情况下应降低黄色基准点，以此调整紧急赶工的力度，保证项目工期，如图3所示。

此时黄色基准点的调整规则如下

其中By（i+1）表示活动i+1的黄色缓冲线设置值，By（i）表示活动i的黄色缓冲线设置值。

3 案例模拟

本文结合一个实际案例，将本文方法与静态三分监控法和相对静态监控法进行对比分析，以验证本文方法的有效性。所选取项目[20]的关键链为A→B→C→E→F→H→J。

本文在确定项目缓冲尺寸时参考了张俊光等[5]的计算方法，得到项目缓冲大小为37天。进一步根据缓冲分配方法和紧急赶工设置方法，可以得到具体的缓冲分配量和最大可赶工时间计算如表1所示，以关键链工序为例。

考虑到项目中各个活动的工期服从右偏的对数正态分布[25]，当X=eY时，表明工期X服从对数正态分布，其中Y为正态分布的随机变量。若Y的平均值为μ，标准差为σ，则X的均值和标准差分别是μx=e（μ+σ2/2）、σx=μ2x（eσ2-1）。令X的均值与活动的计划工期Ti相同，因此随机变量Y的平均值和标准差为

因此，在项目模拟过程中，根据每组Y的均值和标准差取值，结合MATLAB中的对数正态分布随机矩阵函数X=lognrnd（mu，sigma），可以产生活动的每次模拟的随机工期。

采用MATLAB软件对本文监控方法和两种静态方法进行1000次的重复实验模拟，得到三种方法各区域的预警频次表现如表2所示。

由表2可以看出随着活动的执行，静态监控方法各活动缓冲落入黄色和红色区域的次数呈现递增趋势，这是由于缓冲设为定值且在监控过程中无法实现再計划;相对监控方法在这方面做出了一定的改进，三个缓冲区的预警频次表现相较于静态监控方法有了较大的进步，但仍存在红色区域预警次数递增的趋势;本文监控方法各活动缓冲落入黄色和红色区域的频次都呈现出递减的趋势，且多数情况下缓冲落入绿色区域，这表明本文监控方法通过缓冲分配以及实时的监控点调整实现了监控效果的大幅提升。

根据实验模拟结果，得到三种监控方法在工期和成本两方面的性能对比情况。

在工期表现方面，三种监控方法的工期分布较为一致，都在计划完工期之内。结合预警频次表现，可以发现传统监控方法工期较短的原因在于对项目缓冲的不合理利用导致了频繁的错误预警，从而通过增加人力、物力的方式进行不必要的赶工来达到缩短工期的目的。

在成本表现方面，静态监控方法、相对监控方法和本文监控方法的平均成本分别是556651元、523030元、491670元。从仿真成本分布可知，本文监控方法的成本更集中于较低的成本一侧，偏于低成本一侧的趋势更加明显，这说明本文监控方法在成本表现上有着较大的优势，相对于本文的缓冲监控方法，静态缓冲监控方法的成本均值增加了13.22%，相对缓冲监控方法的成本均值增加了6.38%，且本文监控方法的成本均值仅超过项目计划成本的2.73%。这是由于本文提出的缓冲监控方法通过在项目执行过程中对缓冲监控点的实时调节，使得缓冲的分配利用更加贴合于项目的实际情况，由此避免了不必要的人力、物力浪费，使得成本有所下降。

综上所述，本文提出的缓冲监控方法能够在保证项目完工期的同时降低项目成本负荷，原因可以归纳为以下两点：第一，本文监控方法实现了项目缓冲的合理分配，结合活动CRI，在缓冲分配中考虑了活动的不确定性。第二，本文监控方法根据项目的实际执行情况对活动监控点进行调整，有效减少了黄色和红色预警频次，大大降低了成本。在实际应用中，本文提出的缓冲监控方法更加适合应用于注重成本表现、对工期仅要求按时完工的项目，不适合工期优先、以工期提前为目标的项目。

4 结论与启示

本文考虑了项目执行过程中的不确定性及各活动之间的联系，提出在项目计划阶段基于活动CRI对项目缓冲进行合理分配，并将项目活动的缓冲消耗位置信息和速率信息引入缓冲监控中，根据项目前一活动缓冲消耗的位置信息反映项目当前的实际执行情况，并以此预测下一活动的延误情况，进一步根据缓冲消耗速率信息实时调整项目的监控强度即调整两个监控基准点的位置，从而实现了项目缓冲的动态监控。最后，通过蒙特卡洛模拟实验将本文监控方法与传统缓冲监控方法进行了对比，从预警频次、工期和成本等方面进行了分析和比较，验证了本文方法的有效性。

基于当前项目管理中进度超期、成本超支以及资源争夺等现象的频繁发生，为提高项目管理成功率，提出以下两方面的管理启示：（1）构建项目缓冲分配策略，分散整体风险。研究结果表明，根据活动对缓冲进行分配的自适应缓冲监控方法的预警频次表现要优于对比的两种方法，能够对项目风险进行有效分担。为此，可根据项目特点设计分阶段或分活动的缓冲分配策略，精细化管理项目缓冲。（2）设置动态监控触发机制，合理化监控行为。研究结果表明，自适应缓冲监控方法在项目执行中动态调整了监控基准点，减少了错误预警带来的成本浪费，在保证工期的基础上降低了项目成本。为此，可根据项目前期的缓冲消耗情况分析并评估后续活动的延误概率，从而动态调整监控的频率、强度，以减少一味的盲目赶工。

本文的一个不足是没有考虑项目活动的开工柔韧性。在现有的缓冲分配和监控研究中，都存在一个默认的假设，即项目活动的开工柔韧性为无穷大，即不管前一活动何时完工，后续活动总是能马上开工，但是这在现实项目中是不存在的，例如当前活动提前完工了5天，但后续活动因为资源到位等原因无法立即开工。因此本文后续将考虑项目活动的开工柔韧性，对缓冲监控机制进行进一步完善。

参 考 文 献：

[1] Goldratt E M. Critical chain[M]. New York： The North River Press， 1997. 199-210.

[2]施骞，王雅婷，龚婷.项目缓冲设置方法及其评价指标改进[J].系统工程理论与实践，2012，32（8）：1739-1746.

[3]胡雪君，崔南方，赵雁.基于活动工期风险和资源约束风险的缓冲大小计算方法[J].控制与决策，2016，31（8）：1513-1518.

[4]Zhang J， Song X， Diaz E. Buffer sizing of critical chain based on attribute optimization[J]. Concurrent Engineering， 2014， 22（3）： 253-264.

[5]徐小峰，郝俊，邓忆瑞.考虑多因素扰动的项目关键链缓冲区间设置及控制模型[J].系统工程理论与实践，2017，37（6）：1593-1601.

[6]张俊光，冉文娟，贾赛可，等.关键链项目缓冲设置研究述评与展望[J].管理评论，2017，29（12）：195-203.

[7]Dan T. The effect of systemic errors on optimal project buffers[J]. International Journal of Project Management， 2005， 23（4）： 267-274.

[8]Leach L P. Critical chain project management[M]. London： Artech House Inc， 2005. 99-126.

[9]Kuo T C， Chang S H， Huang S N. Due-date performance improvement using TOC’s aggregated time buffer method at a wafer fabrication factory[J]. Expert Systems with Applications， 2009， 36（2）： 1783-1792.

[10]Bevilacqua M， Ciarapica F E， Giacchetta G. Critical chain and risk analysis applied to high-risk industry maintenance： a case study[J]. International Journal of Project Management， 2009， 27（4）： 419-432.

[11]Gonzalez V， Alarcon L F， Yiu T W. Integrated methodology to design and manage work-in-process buffers in repetitive building projects[J]. Journal of the Operational Research Society， 2013， 64（8）： 1182-1193.

[12]別黎，崔南方.关键链动态缓冲监控方法研究[J].中国管理科学，2010，18（6）：97-103.

[13]别黎，崔南方，田文迪，等.基于活动敏感性的动态缓冲监控方法研究[J].中国管理科学，2014，22（10）：113-121.

[14]徐小峰，李想，刘家国.项目关键链资源计划进度偏差预警控制模型[J].系统工程学报，2014，29（6）：845-851.

[15]Martens A， Vanhoucke M. A buffer control method for top-down project control[J]. European Journal of Operational Research， 2017， 262（1）： 274-286.

[16]刘志清，高浩瀚，安沫霖，等.基于完工概率修正的关键链法项目进度优化[J].山东大学学报（工学版），2018，48（1）：104-111.

[17]淦未宇，仲伟周.前瞻性项目控制方法初步研究[J].预测，2004，23（4）：52-55.

[18]Zhang J， Shi R， Diaz E. Dynamic monitoring and control of software project effort based on an effort buffer[J]. Journal of the Operational Research Society， 2015， 66（9）： 1555-1565.

[19]宋喜伟.基于缓冲的软件项目动态混合监控方法研究[D].北京：北京科技大学，2015.

[20]张俊光，万丹.关键链项目实时滚动监控方法研究[J].中国管理科学，2018，26（4）：171-179.

[21]郭海燕.基于质量约束的CCPM缓冲区动态管理研究[D].邯郸：河北工程大学，2013.

[22]胡雪君，王建江，崔南方.基于统计过程控制的两阶段缓冲监控方法[J].控制与决策，2020，35（6）：1453-1462.

[23]Vanhoucke M. Using activity sensitivity and network topology information to monitor project time performance[J]. Omega， 2010， 38（5）： 359-370.

[24]Hu X， Cui N， Demeulemeester E， et al.. Incorporation of activity sensitivity measures into buffer management to manage project schedule risk[J]. European Journal of Operational Research， 2016， 249（2）： 717-727.

[25]Tukel O I， Rom W O， Eksioglu S D. An investigation of buffer sizing techniques in critical chain scheduling[J]. European Journal of Operational Research， 2006， 172（2）： 401-416.