基于PFM 控制的高效GaN 全桥LLC谐振变换器设计
高圣伟,贺 琛
(天津工业大学 电工电能新技术天津市重点实验室机械工程学院博士后流动站,天津 300387)
0 引 言
目前DC-DC 变换器是当代变换器的主流,被人们广泛关注,其效率问题一直是一个热门话题,而LLC 谐振变换器利用谐振腔发生谐振,使原副边实现软开关的特性,提高了效率,成为了DC-DC 变换器的佼佼者。为了增大输出功率以及减小开关管的应力,相关学者提出了全桥LLC 谐振变换器的拓扑结构,此结构原边由4 个开关管进行逆变,副边由4 个二极管进行全波整流,此拓扑结构相对于半桥LLC 谐振变换器能承受更大的功率,运行起来更加稳定和保险。
LLC 谐振变换器目前正朝着高效化、小型化、高可靠性的方向发展,这就对开关器件提出了较高要求。目前第三代宽禁带半导体包括SiC(碳化硅)、C-BN(立方氮化硼)、GaN(氮化镓)、AlN(氮化铝)、ZnSe(硒化锌)以及金刚石等,其中,考虑成本及开发困难程度后能发展比较好的是SiC 和GaN,其中,最先发展起来的是SiC,其在高温场合具有非常大的性能优势[1-3]。而最近几年流行起来的GaN MOSFET 是一种异质结场效应晶体管,开关速度快、导通电阻低、二维电子气迁移率高、功率密度也有非常大的优势,其广泛应用于各种高频场合,高频低损耗特性和超高的电子迁移速率及空穴迁移速率使其迅速在市场中确定了地位[4-5]。
文献[6-8]给出了高频GaN 驱动的设计方法,文献[8]分析了GaN 器件的开关特性、器件优势及发展现状。
现将GaN 与全桥LLC 谐振变换器相结合进一步提升LLC 谐振变换器的效率和功率密度,本文选用GaN System 公司的GS66508B 型号的贴片GaN。由于其体积较小,此款GaN 不仅可以应对高频提高变换器的效率而且能大大提高变换器的功率密度。本文基于GaN 设计的全桥LLC 谐振变换器输入电压为400 V、输出电压为48 V、输出功率为400 W、谐振频率为400 kHz,其利用PFM 控制将工作频率划分为3 个区域进而找到最高效率的工作频率并以此频率运行,从而形成高效GaN 全桥LLC 谐振变换器。由于GS66508B 型号的贴片GaN 没有体二极管,但具有反向恢复特性,所以仍按有体二极管分析。
1 主电路结构
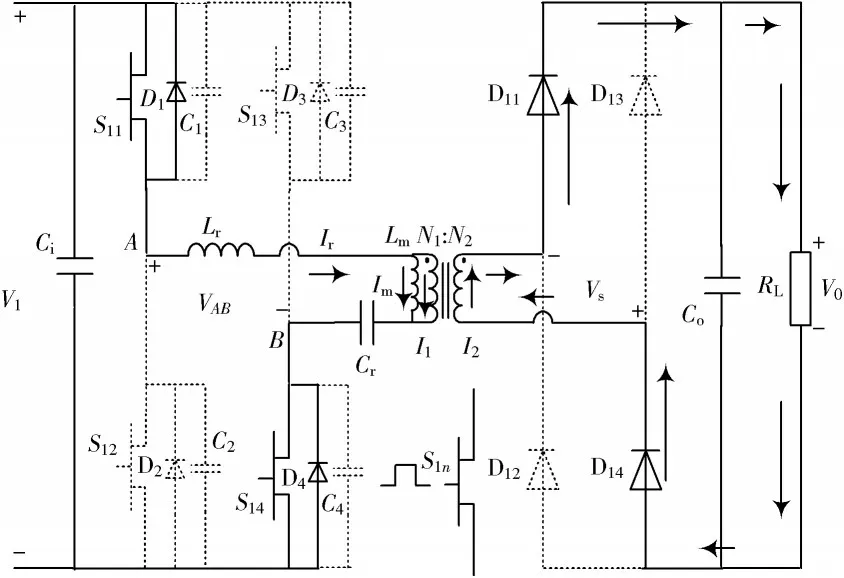
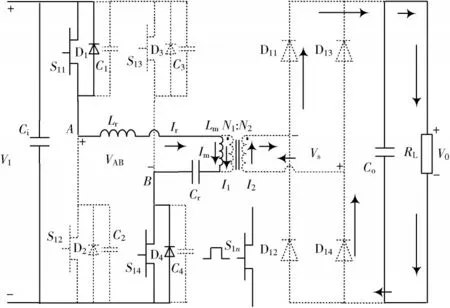
本文设计的全桥LLC 谐振变换器的主电路结构如图1 所示。
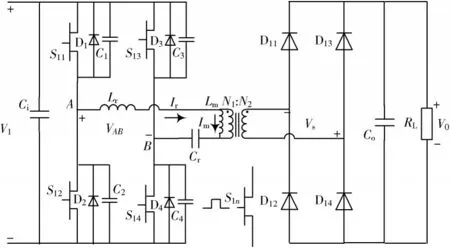
图1 全桥LLC 谐振变换器主电路结构
主电路由方波产生、谐振网络、电压变换、整流滤波以及输出负载5个模块组成。其中,方波产生模块由4个GaN 功率器件组成,且S11,S12的驱动信号互补并设有一定死区(防止直通发生),S13,S14的驱动信号互补并设有一定死区,S11的驱动信号与S14的驱动信号一致,S12的驱动信号与S13的驱动信号一致,然后对驱动信号的频率进行改变从而形成PFM 控制。谐振网络模块由谐振电感Lr、励磁电感Lm以及谐振电容Cr组成,通过开关频率的设定与谐振电容和谐振电感发生谐振的频率fr以及谐振电容、谐振电感和励磁电感共同发生谐振的谐振频率fm进行频率匹配,进而减少损耗,提高效率。电压变换是通过隔离变压器进行交流变换。整流滤波是将交流电压通过4 个二极管进行桥式全波整流,然后经过电容电感进行滤波,最后将符合要求的直流电压施加到输出负载上。
2 工作区域划分
谐振电路阻抗为:
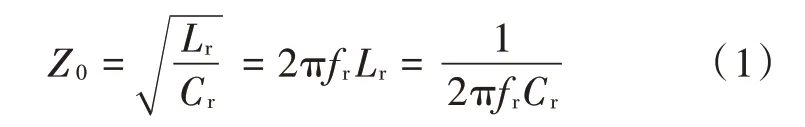
品质因数为:
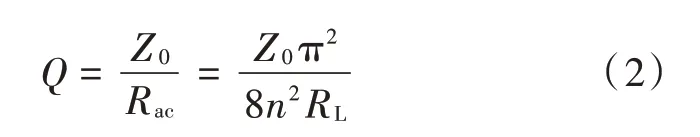
谐振频率为:
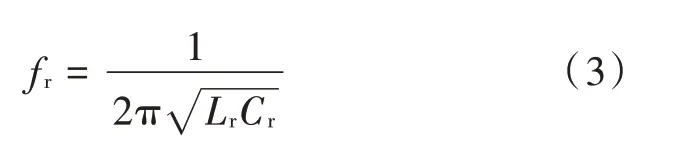
谐振系统完全谐振频率为:
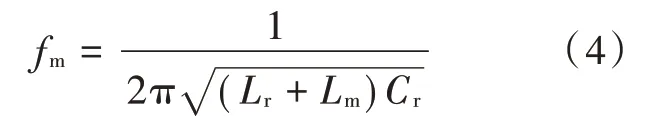
电感归一化量K 为:

综合上述公式可以得出:

综上,可以计算出直流输出增益为:
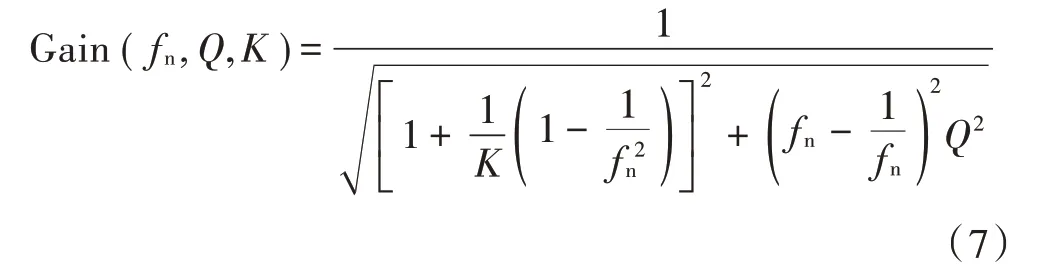
式中:fs为开关频率;fn为频率归一化量[11];fn=
根据式(7)在Matlab 中生成的图像,如图2 所示对全桥LLC 谐振变换器的工作频率进行区域划分。
图2 中虚线K=4,实线K=6,横坐标为fn,把全桥LLC谐振变换器的开环增益作为纵坐标,由式(7)得出当K值固定后开环增益只与fn和Q 有关,以纯阻性曲线为基准,其左边谐振环显容性,变换器副边二极管实现ZCS,其右边谐振环显感性,变换器GaN 器件能实现ZVS。当fs=fr时谐振电感与谐振电容的总阻抗为0,变换器的效率达到最高。由此将LLC 谐振变换器划分为3 个工作区域。
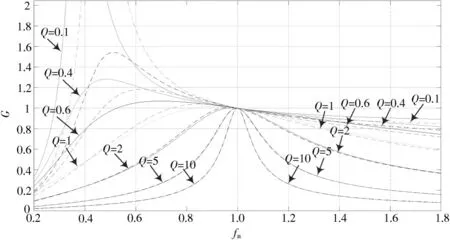
图2 开环增益与归一化频率的关系曲线
如图2 所示,区域3 为fs 由于变换器在区域1,3 原副边只有一侧实现软开关,所以为了研究高效LLC 谐振变换器只考虑区域2。 如图3 所示,模式2 是模式1 的特殊情况,所以只分析效率高的模式1。在模式1 的6 种模态中前3 种和后3 种对称,所以只分析前3 种模态。 图3 PFM 控制方式下变换器工作曲线 模态1(t0~t1):如图4 所示,t0时刻S11,S14处于关断状态,在变换器回路中Lm给C2,C3充电,而C4,C1放电,由于存在电容C1~C4,对S12,S13的开关起缓冲作用,所以S12,S13实现零电压关断,此段时间是非常短的死区时间,Lr中的电流基本不变,Ir=Im。各寄生电容的电压为: 式中IM是通过Lm的最大电流。 图4 模态1(t0~t1) 模态2(t1~t2):如图5 所示,S11和S14实现ZVS,谐振网络输入电压为VAB,Lr和Cr参与串联谐振但Lm被钳位不参与谐振,Im线性增大。VCr,Im及Ir的表达式分别为: 图5 模态2(t1~t2) 模态3(t2~t3):如图6 所示,t2时刻,Ir=Im,此时变压器副边无电流,副边二极管D11和D14实现了ZCS,Lr,Cr和Lm发生共振,因为Lm远大于Lr,所以Ir波动不大但持续时间较长,谐振环为Cr充电,使Cr两端电压线性增加。VCr,Im的表达式分别为: 图6 模态3(t2~t3) 在对全桥LLC 谐振变换器进行参数设计时,首先要确定比例系数K 及品质因数Q 的大小,然后根据公式计算谐振环参数。使LLC 工作在谐振频率下,电压增益为1,所以确定变压器变比n=1 000∶25。 根据基波分析法,得到原边等效电阻: 如图2 所示,K 取值较大时可以提高效率,而且频率变化时造成的增益误差会随着K 值增大而减小,但取值过大又会使电压变化后频率变化范围过大,即一般取5左右,这里取6。 根据式(18)可得,为了减小整个回路中环流峰值,Lm取大一些,所以Cr取小一些,即Q 取大一些。图7 为当K=6 时变换器fn与开环增益的关系,看图中当K=6 时,有没有Q 可以满足增益在一定频率内的调节范围,即Q取0.1~0.6 都满足要求。根据上述Q 值定为0.5。根据式(16)得出:Cr=2.45 nF,Lr=64.51 μH,Lm=387.1 μH。 根据设计参数用Plecs 和Matlab 进行联合仿真,因为Plecs 为电力电子专用仿真软件,用其计算主电路会与实际更加相符,利用Matlab 搭建信号平台与Plecs 主电路结合不仅简单而且仿真结果更加贴近实际。图8为联合仿真平台,图9 为Q=0.5 时各个频率段的仿真输出波形及软开关情况。其中,Vgs为GaN 开关管的驱动信号,Vgs1和Vgs2为变换器同一桥臂不同GaN 开关管的驱动信号,IS为GaN 开关管的导通电流。Io和Vo为全桥LLC谐振变换器的输出电流和输出电压,VD和ID为变换器副边二极管的电压和电流。 图7 开环增益与归一化频率的关系曲线 图8 仿真平台 如图9 所示,根据波形能清楚地发现fs=fr时的输出波形比较规整,而且经仿真验证当变换器工作在fs=fr时达到98%的最高效率。由图9 中变换器各频率段软开关情况可以看出,当开关频率fs小于全振频率fm时原边开关管不能实现ZVS,但副边二极管能实现ZCS;当开关频率fs处于全振频率fm和谐振频率fr之间时原边开关管能实现ZVS 且副边二极管能实现ZCS;当开关频率fs大于谐振频率fr时原边开关管能实现ZVS,但副边二极管不能实现ZCS。所有软开关均已标出,未标记的均未实现软开关,由此可见,本文设计参数完全符合本文第3 节的区域划分,验证了参数的合理性。 根据设计参数搭建实验平台,得到fs=fr时的输出波形图及各频率段效率对比图,得出变换器效率最高的工作频率,使变换器以此频率高效运行。在设计变换器过程中由于寄生参数的存在最终使谐振频率降为了350 kHz,由于频率降低使电感的感抗升高,所以400 V输入时会使输出电压大于48 V。实际输入电压为360 V时,输出电压为48 V。 图9 Q=0.5 时变换器各频率段软开关仿真波形图 图10 为当fs=fr=350 kHz 时的实验输出波形,由图10 中可以看出,变换器实现了ZVS 和ZCS 而且谐振电流波形十分标准,即设计参数可行。 图11 为变换器工作在fr0.5 h 后GaN 的发热情况,图12 为全桥LLC 谐振变换器仿真及实物的效率对比图。 由图11可以看出,本文设计的GaN 全桥LLC 谐振变换器在工作0.5 h后,其GaN器件的最高温度为31.4 ℃,远优于普通器件的发热程度,突显出GaN 器件的优越性。 由图12 中可以看出,无论是仿真还是实物全部都是当fs=fr时效率最高,所以让变换器一直工作在谐振频率便可以一直高效运行,而GaN 器件的引入使全桥LLC谐振变换器的最高效率达96%。 图10 当fs=fr=350 kHz 时的实验波形 图11 变换器工作在fr 0.5 h 后GaN 的发热情况 图12 全桥LLC 谐振变换器仿真及实物效率对比 本文建立基于型号GS66508B 贴片型GaN HEMT 的全桥LLC 谐振变换器系统。首先建立了变换器等效模型,详细分析了PFM 控制下变换器的工作模态,给出了全桥LLC 谐振变换器的区域划分过程,通过PFM 控制找到效率最高的工作频率点,进而让变换器高效工作。最后通过精细化联合仿真和实验对本文全桥LLC 谐振变换器的设计参数进行验证。实验结果证明,本文基于GaN 建立的全桥LLC 谐振变换器不仅功率密度大大提高,最高效率可达96%,且发热量低,系统更加可靠。3 PFM 控制方式下主电路的工作原理
3.1 工作曲线
3.2 工作模态
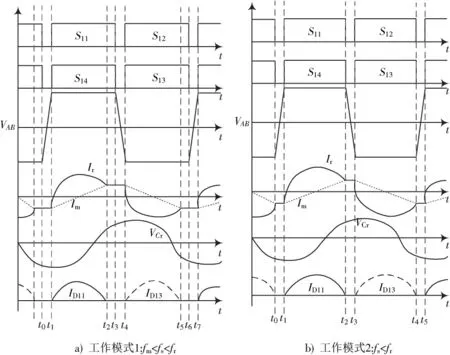
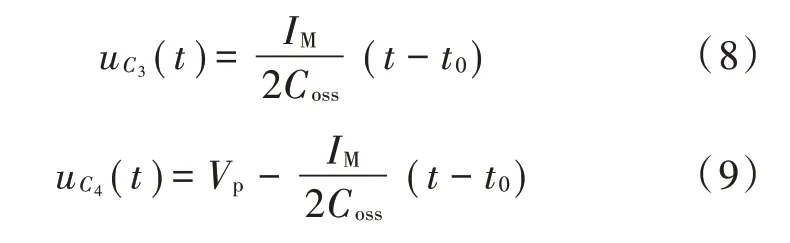

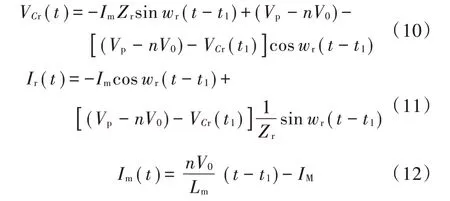

4 参数设计与仿真分析
4.1 参数设计
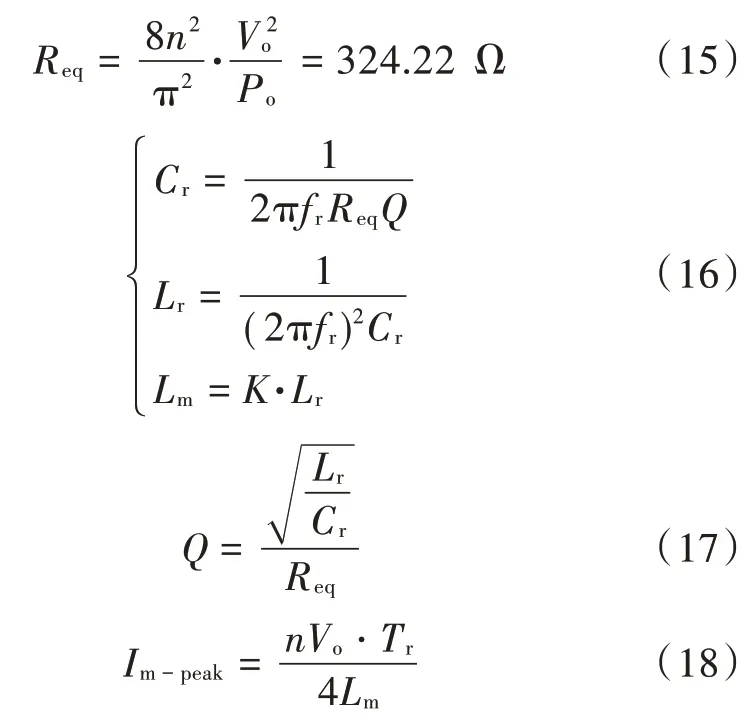
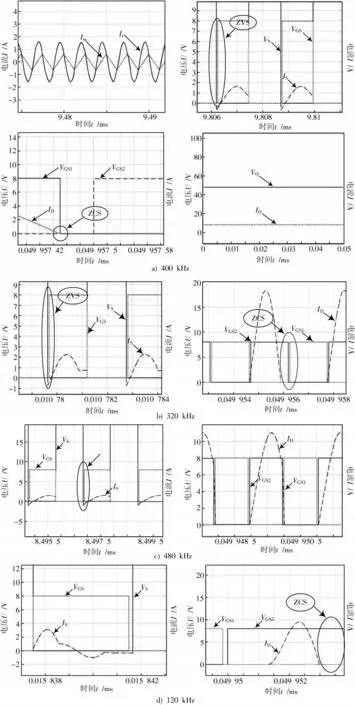
4.2 仿真分析


5 实验分析
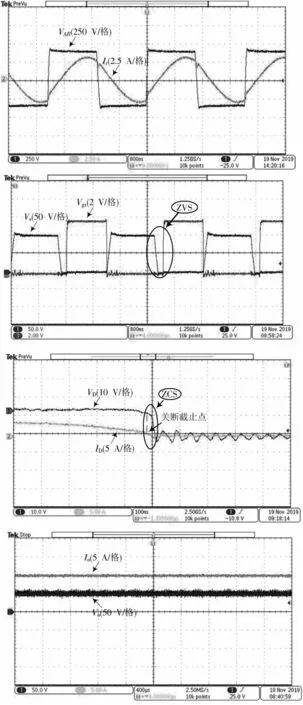

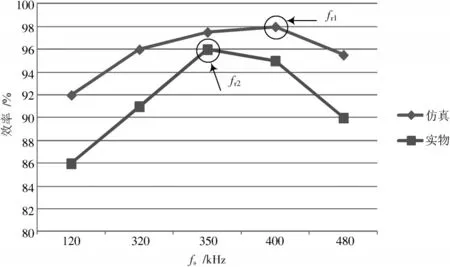
6 结 论

