上行链路MIMO-NOMA 的功率分配方案研究
杨守义,郭天赐
(郑州大学 信息工程学院,河南 郑州 450001)
0 引 言
非正交多址(NOMA)最近被认为是一种有前途的多址接入解决方案,可满足第五代(5G)无线网络严格的服务质量(QoS)要求,例如高光谱效率和大规模连接。NOMA 的工作原理是利用功率域进行多用户复用,在接收端采用连续干扰抵消(SIC)译码,以减少多用户干扰。近几年来,下行链路NOMA 在文献中得到了广泛的研究,并且已经证明在频谱效率和能量效率方面,下行链路NOMA 可以比传统的正交多址(OMA)方案获得相当大的性能增益。
尽管在NOMA 上进行了富有成效的研究,但在大多数现有工作中仅考虑有效载荷功率分配和理想的SIC解码[1]。对于单天线和多天线系统,众所周知,SIC 解码的误差传播限制了NOMA 带来的承诺的性能增益。实际上,误差传播的来源是双重的:一个是信道估计误差(CEE);另一个是数据检测中的错误。本文的重点是通过利用针对给定总能量预算的上行链路MIMO-NOMA系统的导频和有效载荷功率分配之间的非平凡权衡来解决前一问题。具体来说,较高的导频功率会产生更好的信道估计,但会导致数据检测的有效负载功率减少。与此同时,减少的有效负载功率将降低其他用户间的用户干扰(IUI)。因此,联合设计导频和有效载荷功率分配对于减小误差传播至关重要。
本文中为了减轻SIC 中的误差传播,提出了基于实际最小均方误差(MMSE)信道估计器的具有MRC-SIC接收机的上行链路MIMO-NOMA 的联合导频和有效载荷功率分配(JPA)方案。在MRC-SIC 解码过程中,分析每个用户的平均信号干扰加噪声比(SINR)。此外,在每个用户的总能量预算约束下,JPA 设计被描述为一个非凸优化问题,以使最小加权平均SINR(ASINR)最大化。通过几何规划得到了JPA 设计问题的全局最优解。仿真结果表明,所提出的JPA 方案有利于减小误差传播,提高数据检测的性能,特别是在中等能源预算的情况下。
1 系统模型
考虑一个单小区的上行MIMO-NOMA 通信系统,其基站配备了M个天线,为K个单天线用户服务。所有K个单天线的用户都在同一个频带上分配。每个用户通过多个相干时间间隔(CTI)向BS 发送多个帧,其中,假设每个帧的持续时间与CTI 的持续时间相当。每个帧由T导频符号和D 数据符号组成,它们在时间上是连续的。
在帧n 中,分别给出了在导频传输和数据传输过程中BS 接收到的信号。

式中:T ∈CK×T为导频矩阵表示帧n中的数据矩阵;Λ,B 为对角矩阵:
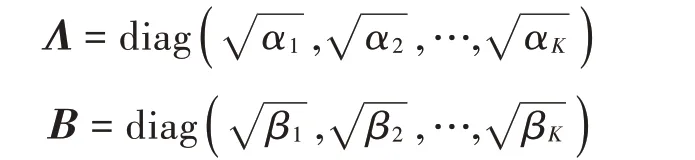
式中αK和βK分别表示用户K 的导频和有效载荷功率。假定归一化正交导频完全分配给所有用户,即TTH=IK,T ≥K。矩阵和表示在帧n 中训练阶段和数据传输阶段具有协方差矩阵σ2IM的加性零均值高斯噪声。矩阵包含帧n 中所有用户的信道。本文采用瑞利衰落假设,即矩阵。标量表示用户k 的大规模衰落,捕获路径丢失和阴影的影响。由于与波长相比,所有用户通常都有足够的间隔,因此假定它们的信道是相互独立的。 因此,用对角矩阵RH=给出了它们的信道相关矩阵。在不丧失一般性的情况下,假设用户按大尺度衰落的降序索引,即在本文中,定义基于大尺度衰落的强用户或弱用户,因为其可以方便地描述跨码字的信道排序,即用户1 是最强的用户,而用户k 是最弱的用户。因此,SIC 解码阶被假定为大尺度衰落的降阶,即用户1,2,…,k 依次解码。
2 ASINR 的性能分析
在MRC-SIC 解码的第k 步中,在取消先前k-1 个用户的信号之后,帧n中的用户k的后处理信号为:
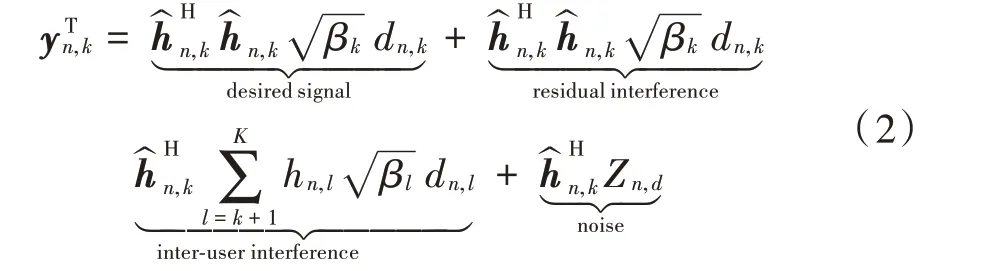


式中E{ ⋅ }表示期望运算。事实上,对于码字级SIC,决定检测性能的是ASINR而不是瞬时SINR。然而,对于数学上的可处理性,在续集中采用的下界为:
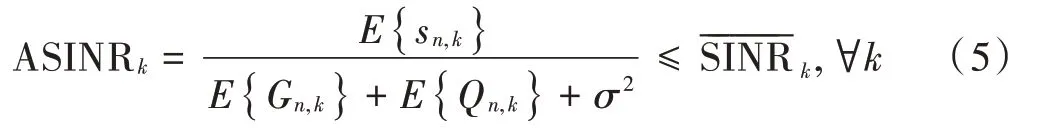
现在,通过下面的定理表示式(5)的闭形。
定理1:对于两个独立随机向量x,y ∈CM×1,定义了一个标量随机变量然后,φ 与y 无关,它分布为的零均值和方差的复高斯分布,即φ~CN。
很明显,给定y 的随机变量φ 是复高斯分布的,其条件均值和方差分别是:
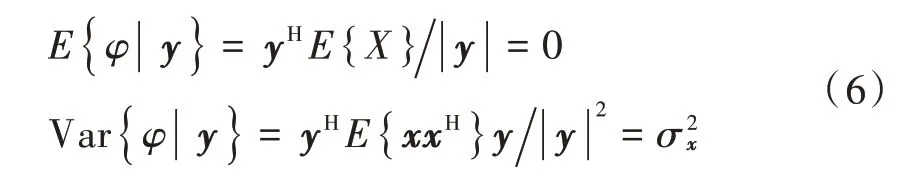
由于φ 的条件均值和方差与y 不相关,因此φ 与y无关,的均值和方差为0。这就完成了证明。
用Φ-1上的矩阵逆引理将E{ sn,k},E{ Gn,k}和E{ Qn,k}替换为:
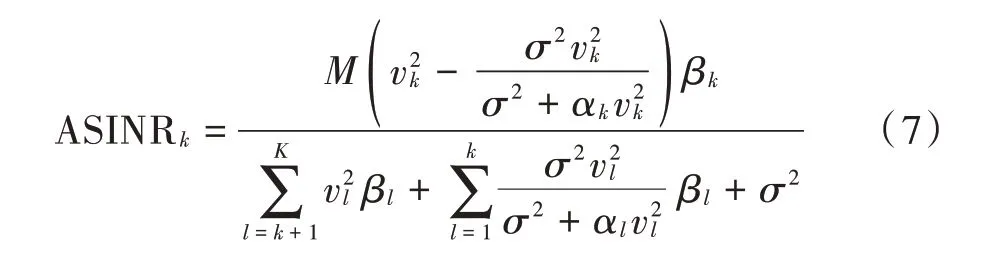
注 意 到,ASINRk随{ α1,α2,…,αk,βk}增 加,但 随{β1,…,βk-1,βk+1,…,βk}减小。换句话说,在导频功率和有效载荷功率的分配之间存在着一种不平凡的权衡。事实上,较高的导频功率αk和用户k 的有效载荷功率βk会导致较高的ASINR。虽然其他用户的有效载荷功率较高,但β1,…,βk-1,βk+1,…,βk将为用户k 引入更多的用户间干扰IUI。
相反,高导频功率的α1,α2,…,αk,βk可以通过提高信道估计质量来减少剩余干扰,有利于提高信道估计精度。
3 联合导频和有效载荷功率分配
JPA 的设计可以使最小加权ASINRk最大化,如下所示:
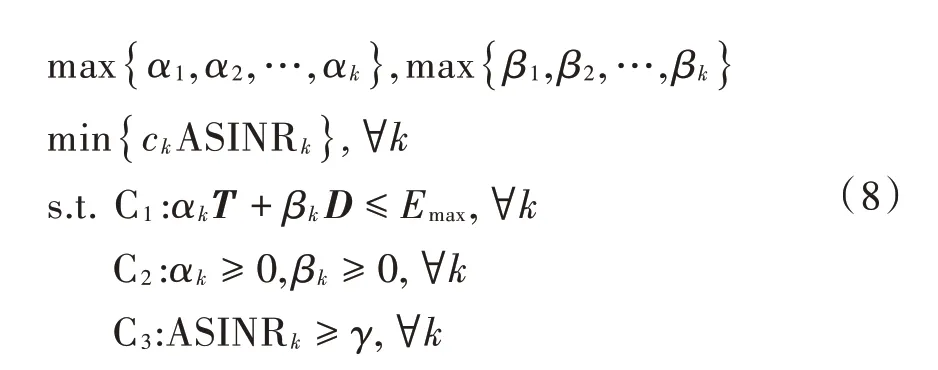
常数c= [ c1,c2,…,ck]是所有k 用户的预定义权重。约束C1将导频功率αk和有效载荷功率βk限制为每个用户的最大能量预算Emax。约束C2保证了αk和βk的非负性。约束C3要求用户k 的ASINR 大于给定的阈值γ,以保证SIC 解码过程中的数据检测性能。由于每个用户的消息仅在BS 上解码一次,因此对于下行链路NOMA,不需要SIC 解码约束[2]。 定义新的优化变量tk=式(8)中的问题等价于以下优化问题:

式中λ >0 是一个辅助优化变量。在此可以很容易地观察到式(9)中约束C1,C3和C4左侧的目标函数和函数都是有效的Posynomial 函数[3]。因此,式(8)中重新形成的问题是标准的几何规划(GP)问题,其可以通过现成的数值求解器,如CVX[10]进行有效地求解。
4 仿真结果
通过仿真验证了本文提出的JPA 方案在非编码和编码系统中的性能分析,并对其性能进行了评估。引入了两种基线方案进行比较,其中等功率分配(EPA)方案设置了相同的导频功率和有效载荷功率,即αk=βk=但是,有效载荷功率分配(PPA)方案只将导频功率固定为并在与式(9)相同的约束条件下,在有效载荷功率βk上进行优化。
在 模 拟 中,设 定M =2,T =K =4,D=96,c=γ=5 dB,Emax=20 J,σ2=-100 dBm。假定CTI 中有T +D=100 个符号。所有的K 用户均匀分布在一个单元中,单元半径为400 m。为了减轻来自先前用户的错误传播的影响,特意选择了权重c。在MRCSIC 解码过程中,未来的工作中将考虑最优的权重选择,采用3 GPP城市路径损耗模型,对所有仿真情况采用正交相移键控(QPSK)调制。对于编码系统,采用3 GPP技术规范[5]中规定的标准Turbo 码。假设一个码字在N =10个相干间隔上传播,这将导致码字长度为1 920 bit。
4.1 独立ASINR
图1 描述了所考虑的三种未编码系统方案的独立ASINR。仿真结果与式(7)中的理论结果吻合较好。此外,可以观察到,提出的方案为用户1 和用户2 提供了比PPA 方案更高的ASINR。这是因为提出的方案比PPA方案更能有效地利用能量。此外,仿真结果也证明了最优功率分配。可以满足式(8)中的能量收支约束C1。
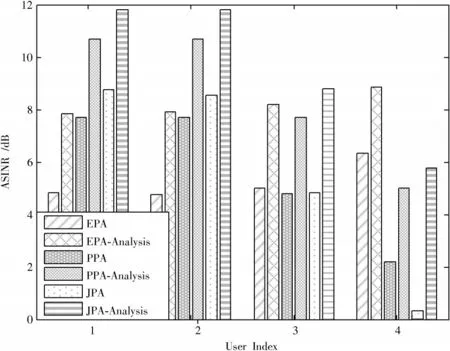
图1 带有MRC-SIC 接收机的上行链路MIMO-NOMA 的独立ASINR
4.2 误码率与能源预算
对于编码系统,图2 显示了本文提出的方案相对于PPA 方案和能源预算Emax的误码率性能。如果式(8)中的优化问题不能考虑失败的惩罚,则设置BER=0.5。可以看到,本文提出的方案为所有4 个用户提供了一个比PPA 方案低的误码率。在中等的Emax环境下,误码率性能的提高是相当可观的。在高Emax状态下,其是边缘的。事实上,在Emax较高的情况下,由于信道估计精度高,残差干扰Qn,k消失了。因此,为了进一步降低误码率,本文方案只能在减轻错误传播的影响方面提供越来越小的收益。在适当的Emax的情况下,本文提出的信道估计方法可以大大改善信道估计,减少MRC-SIC 译码过程中的残余干扰,从而有效地降低误码率。
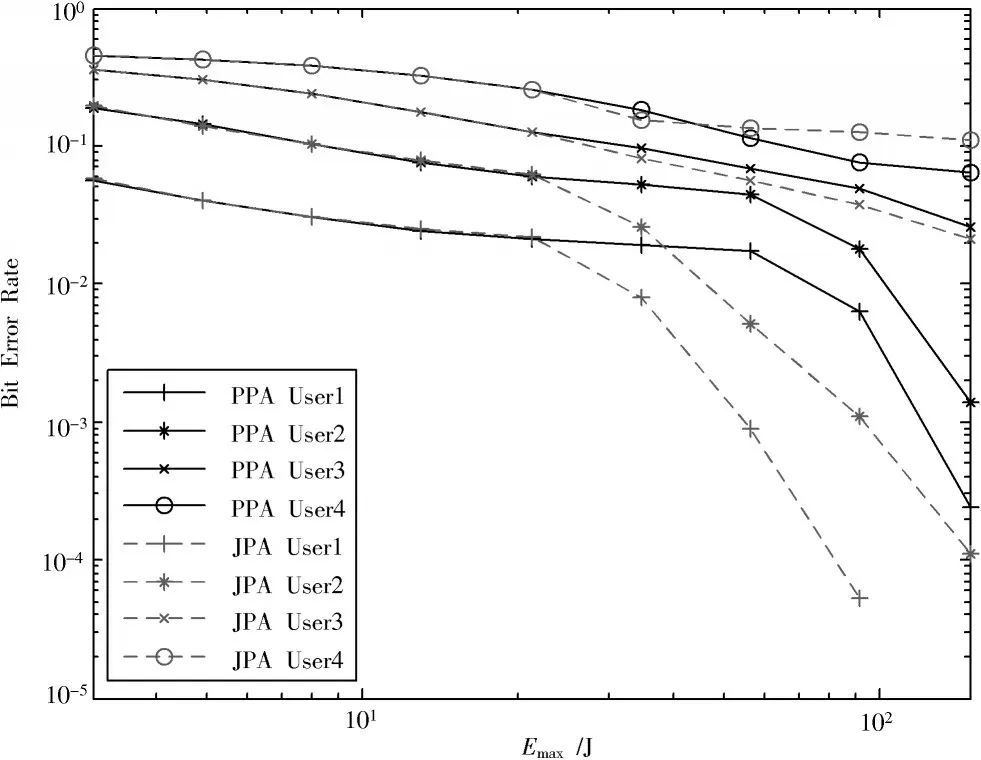
图2 MRC-SIC 接收机上行链路MIMO-NOMA 的BER 性能与能量预算Emax
5 结 语
本文针对具有MRCSIC 接收机的上行MIMO-NOMA系统,提出一种联合导频和有效载荷功率控制方案,以缓解差错传播问题。在考虑信道估计误差(CEE)的情况下,对MRC-SiC 解码过程中的ASINR 进行了分析。将JPA 设计问题描述为一个使最小加权ASINR 最大化的非凸优化问题,并采用几何规划方法求解。仿真结果验证了本文设计分析的正确性,并证明了该方法能够有效地抑制SIC 中的误差传播,提高误码率性能,特别是在适度的能源预算体系中。

