基于伴随优化方法的离心式压缩机回流通道子午面型线的优化设计*
邵伟龙 周 玙 任霁筇 王国欣 郭 伟 闻苏平
(1.西安交通大学能源与动力工程学院;2.沈阳鼓风机集团股份有限公司)
0 引言
多级离心式压缩机的静止元件对整机气动性能的影响很大。随着对离心压缩机研究的不断深入,研究人员发现,静止元件设计不当时,流动损失较大,回流通道的损失系数甚至可以达到0.7~0.8。离心式压缩机基本级性能的进一步提升需要尽可能减小静止元件中的流动损失,因此回流通道的设计和优化问题也成为提高多级离心式压缩机气动性能的研究的焦点问题之一。1998年,Lenke等人[1]就针对回流通道内的三维流动情况做了数值研究,并与实验结果相比较,在设计工况处数值模拟结果与实验吻合较好。Pazzi等人[2]采用人工神经网络的方法研究了决定回流通道几何形状的几组参数之间的关系,如扩压器出口相对直径D5/D2,弯道相对半径r/b2,回流器进口相对宽度b6/b2及出口相对宽度b7/b6,认为当回流器进口相对宽度b6/b2取值偏大或偏小时,弯道半径r和扩压器出口相对直径D5/D2的增加会导致损失系数的降低;当回流器进口相对宽度b6/b2取值适中时,搭配较小的扩压器出口相对直径D5/D2和较大的弯道相对半径r/b2会有比较好的效果。
近些年,回流通道的研究有了较为丰富的进展,在回流通道设计和改进的过程中,弯道的几何形状,回流器叶片数、叶片型线、叶片的厚度分布等因素都被考虑在内。Reutter等人[3]对一多级离心压缩机的回流器叶片做了优化设计,将提高设计点的效率和降低出口气流角的平均偏差作为优化目标,并采用遗传算法控制优化过程。Hildebrandt[4-5]利用进化算法对弯道的子午型线和回流器叶片分别作了优化,在弯道的优化设计方面,以降低总压损失为目标函数,优化后整级的等熵效率提高0.4%;在回流器叶片的优化设计方面,从叶片厚度分布和叶片扭转角的分布两个方向对回流器叶片进行参数化建模,优化过程中同时调整叶片厚度和叶片扭转角的参数,使得总压损失降低了3%。尹熙文[6]通过对回流器叶片参数化建模,对离心式压缩机基本级D-ARV回流器叶片型线进行了优化设计。优化后的回流器三元叶片有效减少了回流器流道内部的流动损失,提高了静压恢复系数并且改善了回流器流道内部的气流分布均匀性。
优化设计是从上世纪中叶开始,随着计算机技术的不断发展而兴起的一门学科。在离心压缩机的优化设计方面,国内外学者的研究成果十分多元化,不仅关注离心叶轮的性能优化,对基本级中的其他部件也有较为深入的研究,研究中也涉及到相当多不同类型的优化理论。Cho等人[11]对离心叶轮的优化研究结合了人工神经网络、进化算法及CFD技术,缩短了优化过程所需的时间,优化计算的精确程度得到提升。Nishida等人[12]对一双级离心压缩机的回流通道进行多目标优化研究,并对优化结果做了实验验证,对回流通道的优化让压缩机整体的效率提升了0.7%。Danilishin等人[13]针对一离心叶轮的轮盖型线和叶片数做了多目标优化,使叶轮多变效率提升了1.58%。国内研究方面,刘小民等人[14]基于多目标遗传算法对离心叶轮叶片及轮盘轮盖型线进行优化,优化叶轮与原始叶轮相比,等熵效率提高1.0%,总压比提高2.5%;程航等人[15]采用人工神经网络和遗传算法对小流量系数离心叶轮进行优化,有效控制了吸力面边界层的发展和叶轮的熵增;刘巍[16]对离心压缩机叶片的优化研究结合了BP神经网络和多目标遗传算法;左曙光等人[17]采用Kriging模型和多目标遗传算法优化离心压缩机的叶片形状,其优化方案将设计点的等熵效率提高了1.02%。
本文采用的伴随方法是梯度类优化方法的一种,其主要特点是计算量与设计变量的数量几乎无关,在流体机械设计愈发精细化的今天,伴随方法的优势逐渐展现出来。在形状优化、最优控制理论、不确定性或敏感性分析,以及数据同化等多个领域中,伴随方法都有较为广泛的应用。在使用梯度类方法的优化设计中,当设计变量数量较多时,常常选用伴随方法来做梯度计算。
伴随方法可分为连续型伴随方法和离散型伴随方法,两种思路区别可以用下图1来表示。

图1 连续型和离散型伴随方法的比较Fig.1 Comparison of continuous and discrete adjoint optimization methods
图1中的思路为连续型伴随方法,下面的思路为离散型伴随方法。在连续型伴随方法中,要先处理流动控制方程,从流动控制方程中推导出偏微分形式的伴随方程,再将伴随方程进行数值离散,得到离散化的伴随方程。而在离散型伴随方法中,则是先离散偏微分形式的流动控制方程,再从离散化的流动控制方程中推导出伴随方程,自然也能得到离散形式的伴随方程。目前,研究者们已经做出了大量的研究来比较两种伴随方法的优劣,但仍然没有得出明确的结论,使用者根据具体情况选择任一种。
本文应用伴随优化方法,对回流通道的子午型线进行优化设计,并分析子午型线的改进对于回流通道内部流动的影响。
1 回流通道子午型线的优化设计
1.1 优化问题定义
回流通道包括基本级的无叶扩压器,弯道及回流器部分,工作介质为空气,流量系数为φ1=0.044,质量流量Qm=1.822kg/s,转速n=5 900r/min,进口温度Tin=293K,进口压力Pin=98kPa。该回流通道子午型线的示意图如图2所示,其主要结构参数如表1所示。

表1 回流通道子午型线的主要结构参数Tab.1 Main structural parameters of the meridian plane profile of the return channel
总压损失系数K的定义如式(1)所示,是指回流通道的压力损失与其进口气流动压的比值,反映了回流通道中流动损失的多少,是衡量回流通道性能的重要指标之一。总压损失系数K越小,说明回流通道中的流动状况越好。将总压损失系数K作为子午型线优化的目标函数,并给定质量流量作为约束条件。优化计算过程中逐步提取流场计算结果,以监测目标函数的变化。

分别在轮盘和轮盖侧的子午型线上布置17个变形控制点,固定回流通道进出口截面的4个控制点不动,其余的控制点均可移动。将这些控制点的纵坐标作为设计变量,可根据计算得到的敏感性信息进行调整,则设计变量总数为30个。
其中,μ为迭代步长,它决定着算法收敛的速度,当取值满足时可保证算法收敛。λmax为自相关矩阵Rxx的最大特征值。tr(Rxx)定义为Rxx所有特征值之和,则tr(Rxx)不小于λmax,即在实际应用中选取μ满足:
1.2 基于Ansys Fluent伴随求解器的优化过程
在Ansys Fluent中,只有先采用Fluent对优化对象的初始流场进行求解,得到完全收敛的流场计算结果,才能调用伴随求解器进行优化计算。因此,在Ansys ICEM中建立上文所述的回流通道的几何模型,并完成网格划分。如图3所示的计算域中共划分网格41 042个,均为结构化网格。壁面附近的边界层网格进行了加密处理,确保y+值控制在10以内。

图2 回流通道子午型线示意图Fig.2 Schematic diagram of meridian plane profile of return channel
利用Fluent对回流通道的二维计算模型进行数值求解,选取k-ε湍流模型,求解器为基于压力的耦合求解器。流动方程、能量方程和湍流方程均采用二阶精度离散。进口边界条件选择速度进口,给出进口处的速度分布;出口边界条件为给定出口静压,壁面边界条件为绝热和无滑移。收敛标准为均方根残差小于10-5,进出口质量流量差小于0.1%。回流通道网格划分如图3所示。

图3 Fluent计算中回流通道的网格划分Fig.3 Meshing of return channels in Fluent
回流通道内初始流场的计算结果如图4所示。

图4 回流通道内流场的计算结果Fig.4 Calculation results of flow field in return channel
设置伴随求解器的离散格式为二阶迎风格式,收敛条件为Adjoint continuity残差小于10-5,进行伴随方程的求解。收敛曲线如图5所示。
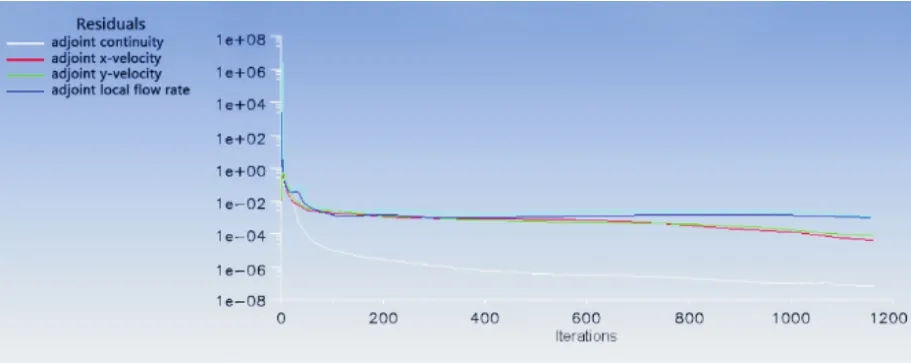
图5 伴随方程求解收敛情况Fig.5 Convergence of adjoint equations
将回流通道进口到出口的总压损失系数K作为目标函数,求解伴随方程,计算收敛后提取敏感性数据并根据敏感性数据调整流场几何外形,更新网格。设置变形参数为0.5,生成新网格后,对目标函数进行评估,若目标函数有明显的降低,则说明仍有优化的空间,继续下一个优化循环。直到目标函数的数值基本稳定,可认为优化计算已收敛。总结每次优化计算中目标函数的变化,得到图6。

图6 目标函数变化历程Fig.6 The course of change in the target function
由图6可以看出,优化循环在10步左右就基本收敛,之后目标函数值保持小幅度波动。经过14个优化循环,回流通道计算模型的总压损失系数K从0.333 3降低至0.316 2,降低了5.1%。
1.3 优化设计结果
图7所示是优化前后回流通道的子午型线,图7中分别用红色和黑色线绘制优化后和优化前的子午型线。可以看出,优化前后,轮盘侧和轮盖侧的型线均有变化。优化后,弯道进口宽度b4减小了约7%,弯道出口宽度b5减小了约13%,弯道部分型线最高点处的流道宽度增加了约8%。
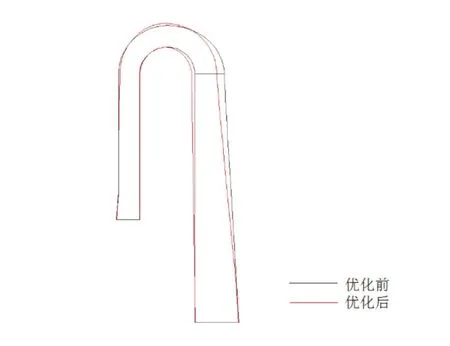
图7 优化前后子午型线对比Fig.7 Comparison of meridian lines before and after optimization
将优化后的子午型线应用到基本级的模型中,重新建模计算,可得到如表2所示的变工况性能。子午型线优化后的基本级,其多变效率ηpol的最高值出现在0.9Qm的工况点,在小流量工况和设计工况点的性能较好。
如图7所示,将子午型线优化前后基本级的性能曲线进行对比。
在设计工况点,优化后的基本级多变效率ηpol从85.37%提高到了85.82%,提高了0.53%,静压比εS提高了0.09%。优化后,多变效率ηpol提高最多的工况点是0.9Qm工况点处,比优化前提高了0.6%。在1.25Qm和1.3Qm的工况点,优化后的基本级多变效率ηpol和静压比εs相比优化前有所降低。
1.4 结果分析
图8比较了子午型线优化前后基本级在0.8Qm~1.2Qm工况范围内的静压恢复系数Cp和总压损失系数K。优化后基本级的静压恢复系数Cp在整个工况范围内都有所提高,设计工况点的静压恢复系数Cp提高了2.8%;同时,小流量工况下静压恢复系数Cp提升的幅度明显大于大流量工况。优化后基本级的总压损失系数K有所降低,在设计工况点降低了2.9%;比较总压损失系数K下降的幅度,小流量工况要好于大流量工况。可以看出,由于优化前的基本级在设计流量及小流量工况的性能本来就好于大流量工况,其多变效率ηpol最高点在0.9Qm处;优化之后这个特点就更加突出。从子午型线的对比也可以看到,优化之后的弯道和回流器部分的流道宽度均有所降低,对小流量工况更有利。

图8 优化前后基本级性能曲线对比Fig.8 Performance curves before and after optimization

为进一步比较弯道部分优化设计前后的流动情况,以原弯道内侧型线的圆心为中心,选取旋转角度分别为0°,30°,60°,90°,120°,150°和180°的七个截面,分别命名为截面1到截面7,如图9所示。
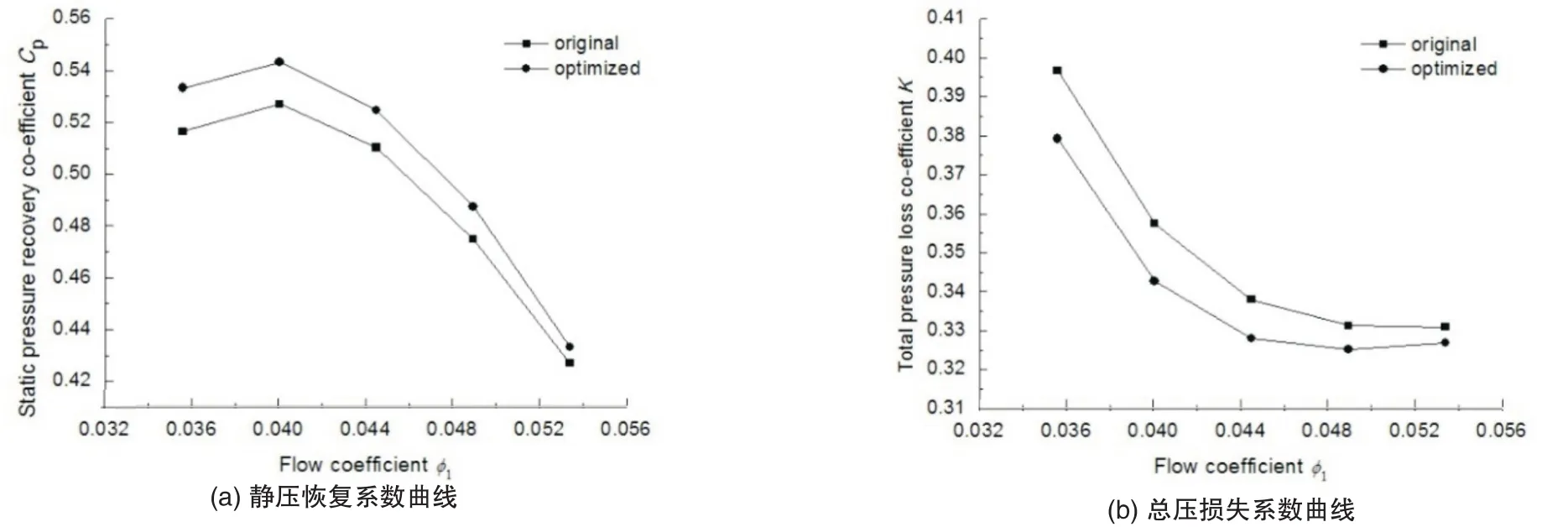
图9 优化前后基本级的静压恢复系数和总压损失系数Fig.9 The static pressure recovery coefficient and total pressure loss coefficient of the basic stage before and after optimization
提取不同截面上子午速度Vm和切向速度Vt的周向平均在设计工况下沿流道宽度的分布,如图10、图11所示。

图10 弯道部分截面示意图Fig.10 A partial section diagram of the bend
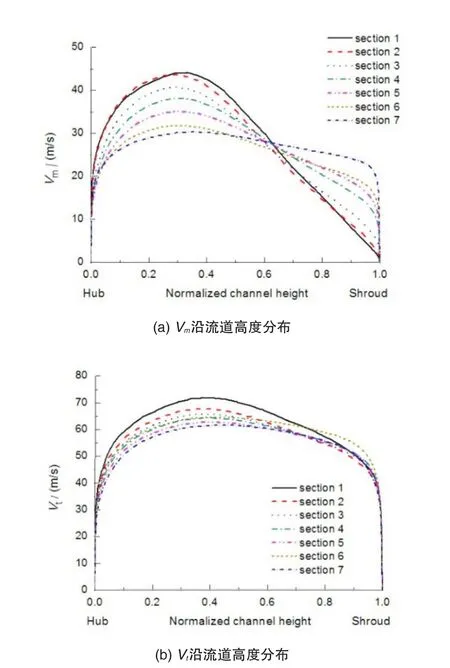
图11 优化前Vm、Vt沿流道高度分布Fig.11 VmandVtdistribute along the height of the return channel before optimization
从弯道进口截面到出口截面,Vm和Vt均呈现逐渐降低、沿流道高度的分布逐渐均匀的趋势。弯道进口截面的气流具有很强的不均匀性,轮盘一侧的气流速度明显高于轮盖侧;气流在弯道中流动,轮盘一侧的子午速度Vm不断降低,轮盖侧的子午速度Vm不断升高,切向速度Vt的分布也因为流速的降低逐渐均匀。优化后的弯道进出口宽度b4,b5均降低,因此优化后的弯道内的子午速度Vm和切向速度Vt整体上略高于优化前;相比较而言,优化后弯道的出口截面上,子午速度Vm的均匀性略好于优化前,Vm的最大值从轮盘侧向流道中心移动。优化前的弯道中切向速度Vt的降低趋势不够明显;优化后的弯道中,切向速度Vt降低的趋势较为清晰,降低的幅度也比较大。因此,从弯道部分流动的均匀性上看,设计工况下优化后的情况要好于优化前。

图12 优化后Vm、Vt沿流道高度分布Fig.12 VmandVtdistribute along the height of the return channel after optimization
2 结论
本文应用Ansys Fluent伴随求解器对回流通道的子午型线进行了优化设计。经过14步优化循环计算,基于离散型伴随方法的优化计算收敛,回流通道计算模型的总压损失系数降低5.1%。优化设计后,弯道进出口宽度b4,b5均降低,使得基本级在设计流量和小流量的变工况下的性能有所提高,其中流量系数φ1为0.04时级多变效率ηpol提高了0.6%,级总压损失系数K降低了4.1%。数值分析回流通道内的气流流动,弯道部分的流动情况有明显改善,流动均匀性提高。

