微量液体的精确加样技术

杨 伟，闫慧敏，和发展

(安图实验仪器(郑州)有限公司，河南 郑州 450016)

引言

近年来，随着国民健康意识的增强，各大医院、检测中心的生化或免疫检测需求量快速上升，这促使全自动化学发光免疫分析仪朝着高速高可靠性的方向发展。加样速度与精度是影响高速高精度检测的关键因素之一[1-3]。由于分析仪是基于抗原抗体的特异性结合机理进行测量，所用样本(血清、血浆等)的加样量都在微升量级，加样精度的降低必然会造成测量结果出现较大偏差，甚至会出现假阳性或假阴性。在单方面追求加样速度的情况下，分析仪的加样精度难免会受到一定的影响[4-6]。因此，在提高加样速度的同时也需要保证样本的加样精度与稳定性。

针对化学发光免疫分析仪在加样过程中存在的加样精度低、稳定性差等问题，本研究在建立加样系统的流体动力学模型的基础上，采用流体仿真与实验验证的方法，分析加样系统的参数对流体运动特性的影响规律，为微量液体高精度加样提供理论支持。

1 系统的组成及工作原理

样本的加样系统主要是通过加样针、泵以及阀等的动作配合，将样本杯中的液体进行精确定量采集并加注至反应杯中。作为仪器检测分析的前处理程序，样本加样的精确性与稳定性直接影响到后续样本测试的结果。

如图1所示，整个加样系统由抽液系统与清洗系统组成。抽液系统主要由加样针、柱塞泵、电磁阀及相应的管路接头等组成，用于样本的精确采集并移液至反应杯中；清洗系统主要由隔膜泵、溢流阀及相应的管路接头等组成，用于样本加注前后的管路冲洗与灌注。柱塞泵为样本的抽取与加注提供动力源，隔膜泵为系统的冲洗与灌注提供动力源。

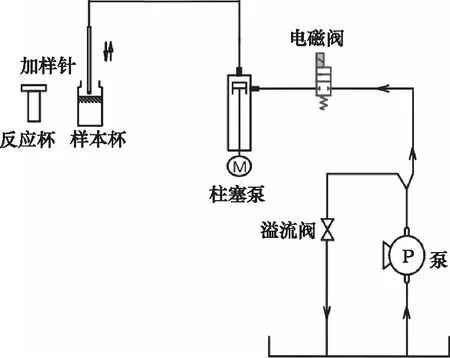
图1 加样系统原理图

样本的加样过程分为样本抽取与样本加注2个过程，如图2、图3所示。整个加样顺序为：抽隔离空气柱→进入样本杯→抽取样本→抬离液面→进入反应杯→注入样本→抬离液面。柱塞泵通过系统液产生压力梯度变化，完成样本的抽取与加注，样本在加样针内部的往复运动，系统液与样本之间通过空气柱隔离[1,3,6]。

图2 样本抽取示意图

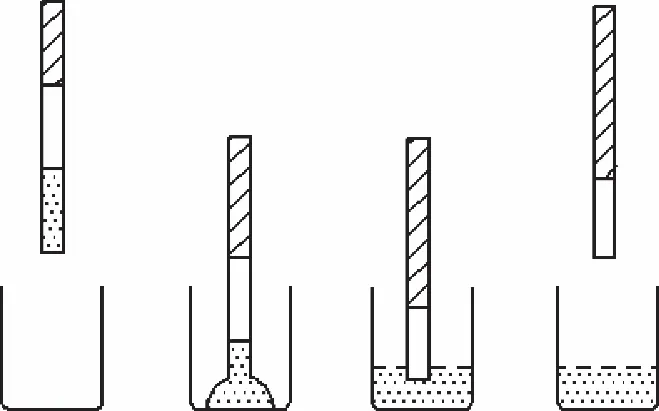
图3 样本加注示意图

2 加样过程的理论分析

为了保证加样过程中样本、空气柱与系统液的动态稳定性，避免样本与系统液的混合，液体的运动特性应为层流状态。由牛顿流体理论可知，层流会受到管壁摩擦因素的影响，靠近管壁的位置流体的摩擦力较大且流速缓慢，流体分层流动[1-3,7]。

根据流动液体的连续方程与伯努利方程，抽注液状态下的流体动力学方程[1,7-9]：

p1-p2=ρu2/2+∑Δp

(1)

式中,p1—— 入口端压力

p2—— 大气压力

ρ—— 液体密度

u—— 入口端平均流速

∑Δp—— 各段管路沿程压力损失与局部压力损失之和

(2)

(3)

式中，ui—— 该段管路中的流速

li—— 该段管路长度

ζi—— 局部压力损失系数

η—— 流体动力黏度

式(1)可以表示为：

(4)

流体定常流动条件下的力学方程：

(5)

式中，f阻—— 流体在近壁面处的阻力

τ—— 切应力

d—— 该段管路直径

上述分析过程中，液体所受重力与表面张力为常量，故理论推导过程中不做特殊要求。

由式(4)与式(5)可知，随着速度u的不断增大，近壁面处的阻力不断增大。由于加样针内外壁面存在一定粗糙度，随着液体的流速加快，壁面位置的流体阻力不断增大，其表面残留的液体会不断增多。

通过以上理论分析可知，在抽液的过程中，残留在加样针内壁的系统液会稀释样本；在注液的过程中，样本会残留在针内壁；加样针抬离样本液面过程中，其外壁面存在样本残留。所以，系统的速度参数对加样的精确性及稳定性存在一定影响。

3 CFD仿真分析

3.1 仿真模型

本研究采用计算流体动力学(CFD)的方法，近似模拟2D或3D模型中流体的运动状态。在满足流体连续性方程、质量守恒方程和动量守恒方程的前提下，对加样针内外壁面附近的液体运动状态进行仿真分析[10-11]。

以加样针为仿真分析对象，应用三维软件建立加样针三维几何模型(图4)。

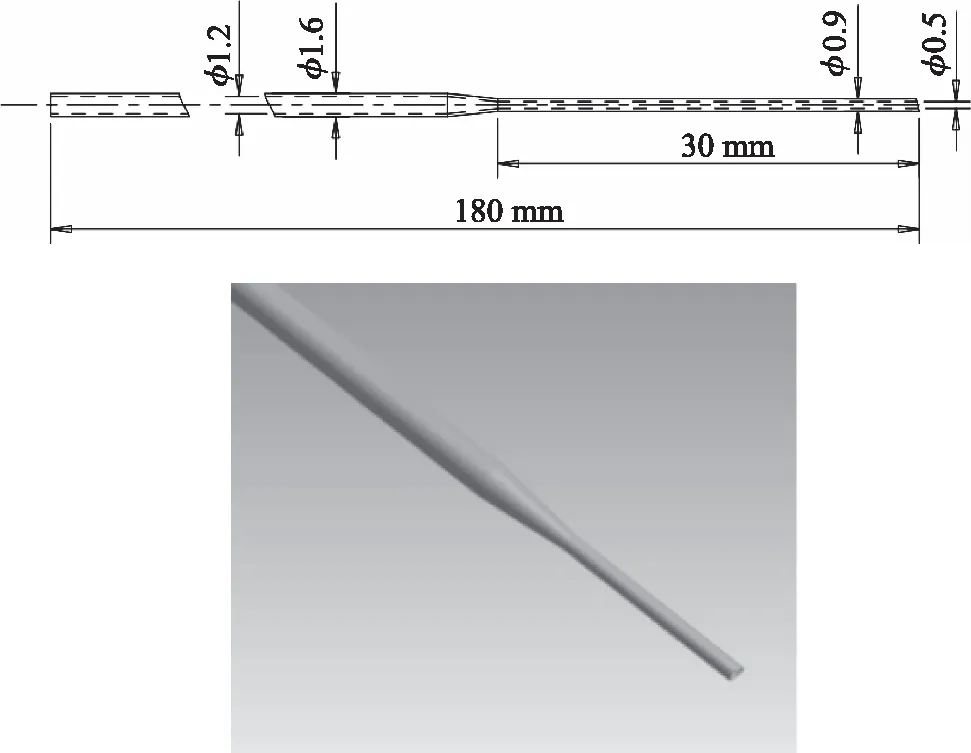
图4 加样针的尺寸参数及三维模型

根据加样针在样本杯与反应杯中的抽注状态，对加样系统的仿真分析模型进行简化。由于几何模型是轴对称结构，本研究采用2D简化模型进行仿真分析，如图5、图6所示。

图5 加样系统2D简化图 图6 网格划分示意图

3.2 仿真参数设置

1)材料物性

采用纯化水代替人体体液样本(血清、血浆等)。

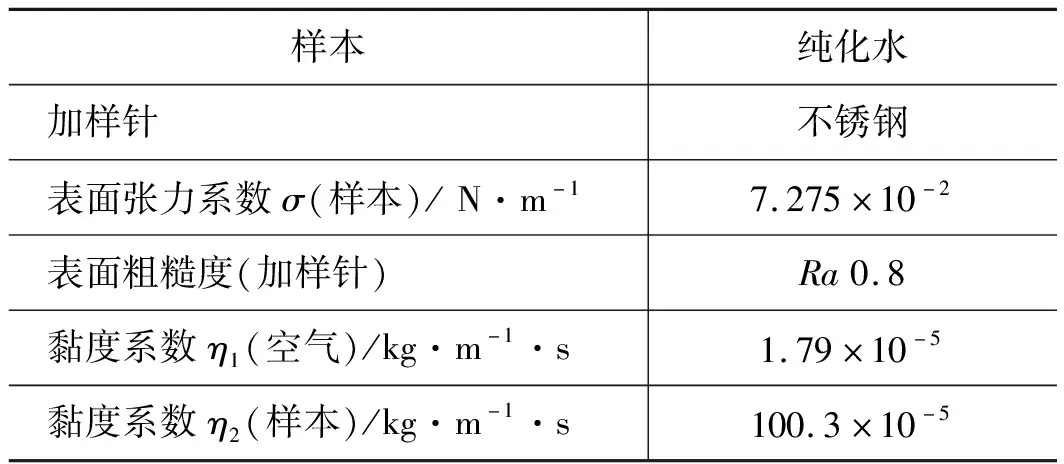
表1 物性参数

2)边界条件及网格设置

在满足流体连续性，质量守恒和动量守恒前提下，采用多相流VOF模型与标准k-ε方程对仿真模型进行求解。在考虑重力加速度条件下，两相介质分别是空气和纯化水，加样针内外壁面分别设置一定的粗糙度[12-15]。采用动网格技术，根据不同的工况设置不同的边界条件(如图7所示)。对整个加样系统进行分区处理，采用滑移网格处理动静交界面，并借助弹性光顺与局部网格重构技术对网格实时更新。

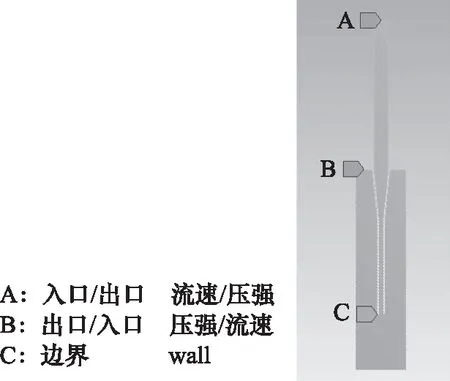
图7 边界条件示意图

为了更加直观的反应液体的运动特性，本研究仅对加样完成后针的抬升速度与样本抽液过程进行仿真分析，复现不同的加样针运动速度及样本抽注液速度对加样系统的影响规律。

3.3 仿真分析

1)加样针抬升速度的仿真分析

设定样本加注完成后，加样针浸入液面下的深度为3 mm，对加样针抬离液面后针外壁面的残液量进行仿真分析。随着加样针的不断抬升，液体在针外壁面的运动状态如图8所示，深色表示液体，浅色表示空气。不同抬升速度条件下，加样针外壁面的残液量如图9所示。

图8 针外壁面液体的运动示意图

图9 抬升速度u对应残液量V

如表2所示，由仿真结果可知，加样针外壁面的液体在张力的作用下，其克服自身重力作用浸润在针的外壁面；随着加样针抬升速度的逐渐增大，针外壁面的残液量不断增多。

表2 抬升速度u对应的残液量V

2)样本抽取速度的仿真分析

设定样本抽液量为10 μL，系统液在加样针内部上升距离为8 mm，对系统液在针内壁面的残液量进行仿真分析。随着加样针内部系统液的不断上升，液体在针内壁面的运动状态如图10所示，深色表示液体，浅色表示空气。不同抽取速度条件下，加样针内壁面的残液量如图11 所示。

图10 针内壁面液体的运动示意图

图11 抽取速度u1对应残液量V

如表3所示，由仿真结果可知，加样针内壁面的液体在张力的作用下，其克服自身重力作用浸润在针的内表面；随着抽液速度的不断增大，加样针内表面的残液量不断增多。

表3 抽取速度u1对应的残液量V

综上可知，加样针注完样本后针抬升的速度越快，针外壁面的残液量越多，注入反应杯中的样本减少，样本加注的精确性下降；抽取样本的速度越快，针内壁面的系统液残液量越多，样本稀释的现象越严重，实际注入反应杯中的样本越少。同理，加样针抽完样本后抬升的速度越快，针外壁面的残液量越多，在进行样本加注的过程中，针外壁的液体与加注反应杯中的液体交互不可控性增大，样本加注的精确性下降；加样针注液速度越快，样本残留在针内壁的残液越多，注入反应杯中的样本减少。

4 实验研究

搭建样本加样实验平台，如图12所示。柱塞泵采用500 μL高精度微型柱塞泵，分辨率为0.25 μL/step；系统管路为1.6 mm×3.2 mm；柱塞泵至加样针的管路长度为1.8 m。分别对样本的抽注液速度及加样针的运动速度进行实验验证，分析不同的速度参数对加样精确性及稳定性的影响。

图12 加样系统实验平台

实验过程中使用的计量设备，如图13所示。加样实验平台使用专用软件控制，加样针的抬升速度与抽液速度用单位时间内其移动的距离与抽液体积反算得到。

图13 分光光度计与高精度电子天平

4.1 加样针抬升速度的实验与分析

1)抽取样本后针抬升速度的实验

为了保证实验的精确性，排除抽取样本引入的误差影响，实验过程中加样针不抽取样本，对针抬离液面后针外壁面的残液量进行实验研究，分析其对加样的精确性与稳定性的影响。

采用加样实验平台(如图12所示)，设定加样针进入液面下的深度为8 mm，在不同的抬升速度条件下(如表2所示)，加样针反复进入样本杯10次，求取样本杯每次减少液体量的均值与变异系数CV。实验采用高精度电子天平(十万分之一)对样本的量进行称量并反算出液体的体积，加样针每次进入样本杯之前均用吸水纸拭去表面液体，实验结果如图14所示。

图14 抬升速度u对应的残液量V与CV值

由实验结果可知，随着加样针抬升速度的不断增大，针的外壁面残液量不断增大，其曲线呈“S”形变化；随着加样针抬升速度的不断增大，变异系数CV不断增大，其残液量的稳定性降低。

2)加注样本后针抬升速度的实验

为了保证实验的精确性，排除加注样本引入的误差影响，实验过程中加样针不加注样本，对针抬离液面后针外壁面的残液量进行实验研究，分析其对加样的精确性与稳定性的影响。

采用加样实验平台(如图12所示)，设定加样进入液面下的深度为3 mm，在不同的抬升速度条件下(如表2所示)，加样针反复进入反应杯10次，求取反应杯每次减少液体量的均值与变异系数CV。实验采用高精度电子天平(十万分之一)对样本的量进行称量并反算出液体的体积，加样针每次进入反应杯之前均用吸水纸拭去表面液体，实验结果如图15所示。

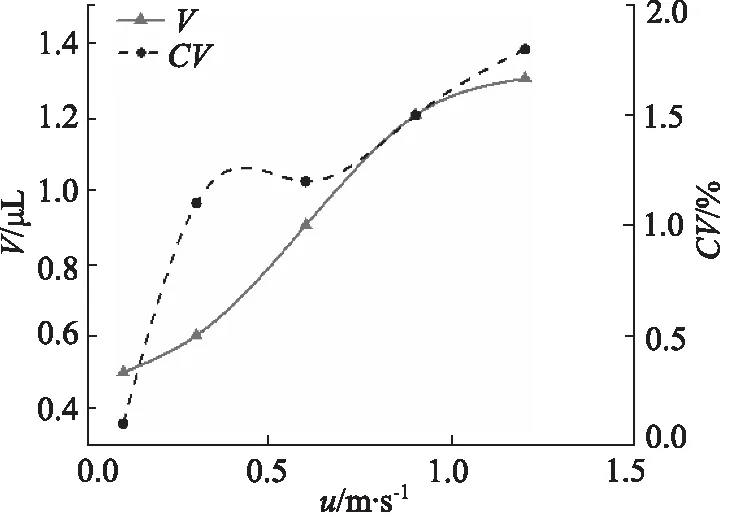
图15 抬升速度u对应的残液量V与CV值

由实验结果可知，随着加样针抬升速度的不断增大，针的外壁面残液量不断增大，其曲线呈“S”形变化；随着加样针抬升速度的不断增大，变异系数CV不断增大，其残液量的稳定性降低。

综合以上实验验证可知，加样针抬离液面的速度越快，针外壁面的残液量越多，其残液量的变异系数CV增大。随着抬升速度的不断增大，加样针抽取样本后针外壁面的残液量越多，样本加注的过程中实际加入反应杯中的样本与针外壁的样本交互的不可控性越大，样本加注的精确性与稳定性下降；随着抬升速度的不断增大，加样针加注样本后针外壁面的残液量越多，样本被针外壁带走的不可控性越大，样本加注的精确性与稳定性下降。

4.2 抽注液速度的实验与分析

1)抽取样本速度的实验

设定加样针抬升速度与加注样本的速度，在其他条件不变的条件下，改变加样针的抽取速度，对加样针抽取样本后针内壁面的残液量进行实验，分析其对加样的精确性与稳定性的影响。

采用加样实验平台(如图12所示)，设定样本抽液量为10 μL，加样针进入液面下的深度为8 mm，加样针抽注完成后抬离液面的速度为0.5 m/s，加注样本的速度0.4 m/s，在不同的加样针抽液速度条件下(如表3所示)，加样针反复加样10次，求取样本稀释比的均值与变异系数CV。实验采用高精度电子天平(十万分之一)与分光光度计对样本的量进行称量并反算出液体的体积，加样针每次进入样本杯之前均用吸水纸拭去表面液体，实验结果如图16所示。

图16 抽取速度u1对应的样本稀释比α及CV值

由实验结果可知，随着抽液速度的不断增大，加样针内壁的系统液残液量不断增多，样本的稀释比值不断增大，其曲线呈“S”形变化；随着加样针抽液速度的不断增大，变异系数CV不断增大，其注液量的稳定性降低。

2)加注样本速度的验证

设定加样针抬升速度与抽取样本的速度，在其他条件不变的条件下，改变加样针的加注速度，对加样针加注样本后针内壁面的残液量进行实验，分析其对加样的精确性与稳定性的影响。

采用加样实验平台(如图12所示)，设定样本注液量为10 μL，加样针加注完成后，样本针浸入液面下的深度为3 mm，加样针加注完成后抬离液面的速度为0.5 m/s，抽取样本的速度0.4 m/s，在不同的加样针注液速度条件下(如表3所示)，加样针反复加样10次，求取样本量的均值与变异系数CV。实验采用高精度电子天平(十万分之一)对样本量进行称量并反算出液体的体积，加样针每次进入反应杯之前均用吸水纸拭去表面液体，实验结果如图17所示。

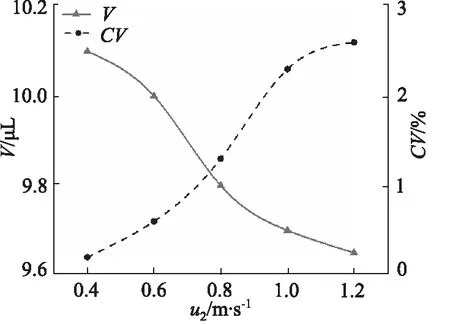
图17 加注速度u2对应的样本量V与CV值

由实验结果可知，随着注液速度的不断增大，加样针内壁的样本残液量不断增多，加注的样本量不断减少，其曲线呈“S”形变化；随着加样针注液速度的不断增大，变异系数CV不断增大，其注液量的稳定性降低。

综上可知，加样针抽液与注液的速度越快，针内壁面的残液量越多，其残液量的变异系数CV增大。随着抽取速度的不断增大，加样针抽取样本后针内壁面的系统液残液量越多，样本稀释比值越大，样本加注的精确性与稳定性下降；随着加注速度的不断增大，加样针注完样本后针内壁面的残液量越多，样本的加注量不断减少，样本加注的精确性与稳定性下降。

5 结论

(1)基于加样系统的流体动力学模型，推导出了系统的速度参数对加样精度的影响因子，并采用仿真分析与实验验证的方法进一步揭示了速度参数对样本的动态稳定性的影响规律，为微量液体的精确加样提供了依据;

(2)加样针抬离液面的速度越快，针外壁面的残液量增多，残液量的波动性增大，加样针外壁面的样本与实际加注的样本交互的不可控性增大，样本加注的精确性及稳定性降低;

(3)加样针抽取与加注样本的速度越快，针内壁面的系统液与样本的残留量越多，样本加注的精确性及稳定性降低;

(4)加样系统的速度参数对加样系统的精确性与稳定性影响比较显著；合理匹配系统的速度参数，有助于改善加样的动态特性，提高加样系统的可靠性；同时，液体的残液量曲线为非线性曲线，在满足加样精度与稳定性的条件下，依据实际的需求选择加样系统的速度参数，有助于提高加样系统的加样效率;

(5)柱塞泵实际运行速度可分为启动速度、停止速度与运行速度，相较于稳定的运行速度，启动速度与停止速度的时间占比相对较小，故未做深入分析。随着仪器对加样性能的不断提升，有必要对启动速度与停止速度深入研究，分析其对加样性能的影响。