基于拐点光顺的七轴龙门式铺丝机插补算法

程 亮，李 宁，郑守国，王 青

(浙江大学 浙江省先进制造技术重点研究实验室，浙江 杭州 310027)

0 引言

碳纤维复合材料因其具备比重小、比强度高和比模量大等优异特点而被大量应用于航空航天等领域[1]。以空客为例，飞机结构中复合材料质量分数从A310-300的5%，上升到A380的25%，再到A400M的35%，甚至在A350中高达52%，且碳纤维复合材料的应用场景由最初的次承力结构逐渐变成主承力结构[2]，对复合材料构件的制造要求越来越高，而自动铺丝技术作为生产复杂型面复合材料构件的关键技术，受到国内外的广泛关注[3-4]，其中，当铺丝机床在连续短线段轨迹上运动时，会在拐点处发生切向和曲率变化不连续的问题，极大地影响机床的控制精度和铺放效率[5]，这早已引起国内外学者和工业界厂商的重视。

为实现拐点光顺过渡，许多研究学者进行了相关研究，采用不同的曲线(圆弧、Bézier曲线、B样条曲线等)对短线段路径进行光顺。吴文江等[6]根据拟合误差将连续短线段区域的控制点转化为二次Bézier曲线，并识别出圆弧段从而进行圆弧插补，但该算法存在曲率不连续的情况；为保证加工机床更加平稳和连续地运动，Sencer等[7]提出了在转角误差的控制下使用单个五次Bézier曲线确保曲率连续的几何角平滑算法，Zhang等[8]在加工路径上采用7个控制点控制的五次B样条曲线保证路径拐角光顺过渡,但是在控制机床末端执行器运动过程中，不仅要保证其满足位置路径平滑过渡，还要保证矢量方向平滑过渡，而上述算法中均未描述如何控制末端执行器矢量方向平滑过渡；Bi等[9]提出三次Bézier曲线分别用于平滑五轴机床的位置路径和路径方向，Zhao等[10]提出双四次B样条曲线近似插补方法，为五轴数控机床生成平滑的刀尖位置路径和方向路径，但是对于五轴以上的铺丝机来说，铺丝机头的控制包括位置控制和两个方向控制，文献[9-10]中的算法均不能完成指定的平滑要求。

本文针对七轴龙门式自动铺丝机的拐点过渡方法进行研究，提出一种基于三次Bernstein-Bézier曲线的插补算法，该算法在相邻线段拐点处采用三次Bernstein-Bézier曲线对铺丝头位置和矢量方向进行局部过渡，并在柔性加减速控制方法的基础上对“直线段+过渡曲线段”的铺放路径进行插补运算，保证七轴自动铺丝机在路径控制点控制的目标路径上平稳连续运动。

1 基于误差约束的过渡曲线模型

1.1 构造一段三次Bernstein-Bézier曲线

通常给定4个顶点Qi(i=0,1,2,3)，可以定义一段三次Bernstein-Bézier曲线Q(u)[11]：

Q(u)=(1-u)3Q0+3(1-u)2uQ1+

3(1-u)u2Q2+u3Q3,u∈[0,1]。

(1)

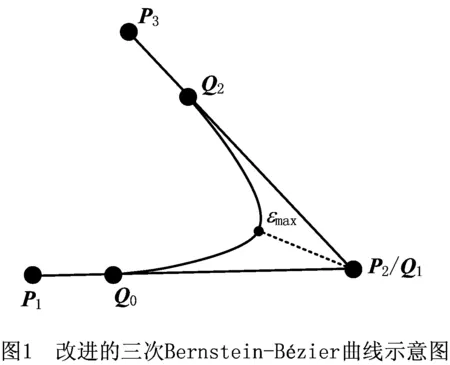
由于铺丝机的末端执行器为柔性压辊，轨迹误差相对于刚性加工机床要求低，为了简化计算并提高曲线的可操作性，调整控制点，使得Q2=Q1，这样可以通过3个顶点控制一段三次过渡曲线，如图1所示。改进后的三次Bernstein-Bézier过渡曲线参数方程为：

Q(u)=(1-u)3Q0+3(1-u)uQ1+

u3Q2,u∈[0,1]。

(2)

式中Q0、Q1、Q2为该三次曲线的3个控制顶点。

1.2 曲率优化

过渡曲线的作用是保证相邻直线段切向连续、曲率连续，因此过渡曲线起点和终点的切向方向应分别与两直线段方向相同，且起点和终点的曲率为0，就能够保证铺丝机从直线段到过渡曲线段的运动过程中，速度与加速度连续。

为求出过渡曲线起点和终点的切线方向，对式(2)进行求导，得到该过渡曲线的导函数为：

Q′(u)=-3(1-u)2Q0+3(1-2u)

Q1+3u2Q2,u∈[0,1]。

(3)

Q(u)在Q0、Q1处的导数为：Q′(0)=3(Q1-Q0),Q′(1)=3(Q2-Q1)，为了保证该过渡曲线分别与需要过渡的两相邻直线段相切，调整控制点，Q1=P2，即令拐点为该过渡曲线控制顶点，就能够保证铺丝机从直线段运动到过渡曲线段时切向变化连续。

根据曲线曲率定义，三次Bernstein-Bézier过渡曲线上对应的曲率

(4)

对式(3)进行求导，得到该过渡曲线的二次导函数：

Q″(u)=6(1-u)Q0-6Q1+6uQ2,u∈[0,1]。

(5)

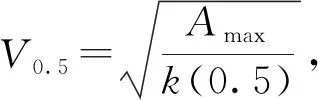
1.3 确定曲线控制顶点的位置

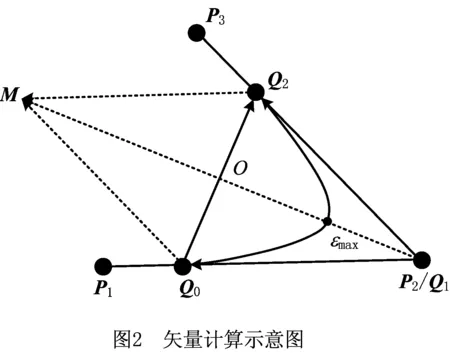
1.2节根据切向变化连续的要求，调整控制点Q1=P2，而Q0和Q2控制过渡曲线与相邻直线段之间的偏差大小，因此它们的位置与轨迹误差εmax有关。

由过渡曲线对称性和凸包性可知，Q(0.5)与拐点P2/Q1之间的距离为过渡曲线与目标轨迹产生的最大误差，因此各控制顶点的计算过程如下：

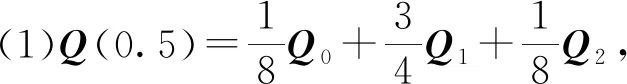
(2)因为|Q1Q0.5|=εmax，所以|Q1O|=4εmax。

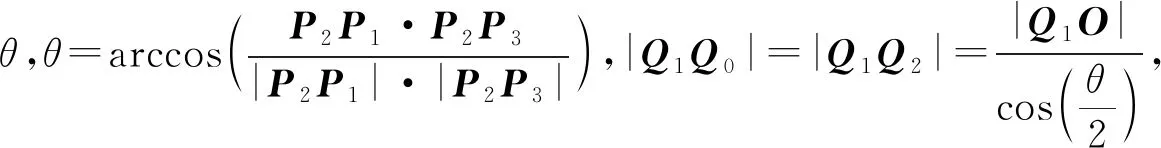
(4)为了提高路径插补算法的协调性和稳定性，将过渡曲线的控制顶点近似成靠近拐点一侧的插补点。

2 柔性加减速控制方法分析

2.1 多种加减速控制方法对比

在对“直线段+过渡曲线段”铺放路径进行插补运算之前，应根据机床约束以及过渡曲线限制速度等条件建立合适的加减速控制方法。

数控机床常用的加减速控制方法主要有直线加减速控制方法、S曲线加减速控制方法和多项式加减速控制方法[12]，为铺丝机选择合适的加减速控制方法，需要考虑加速过渡时间、柔性、计算量等因素。

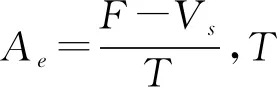
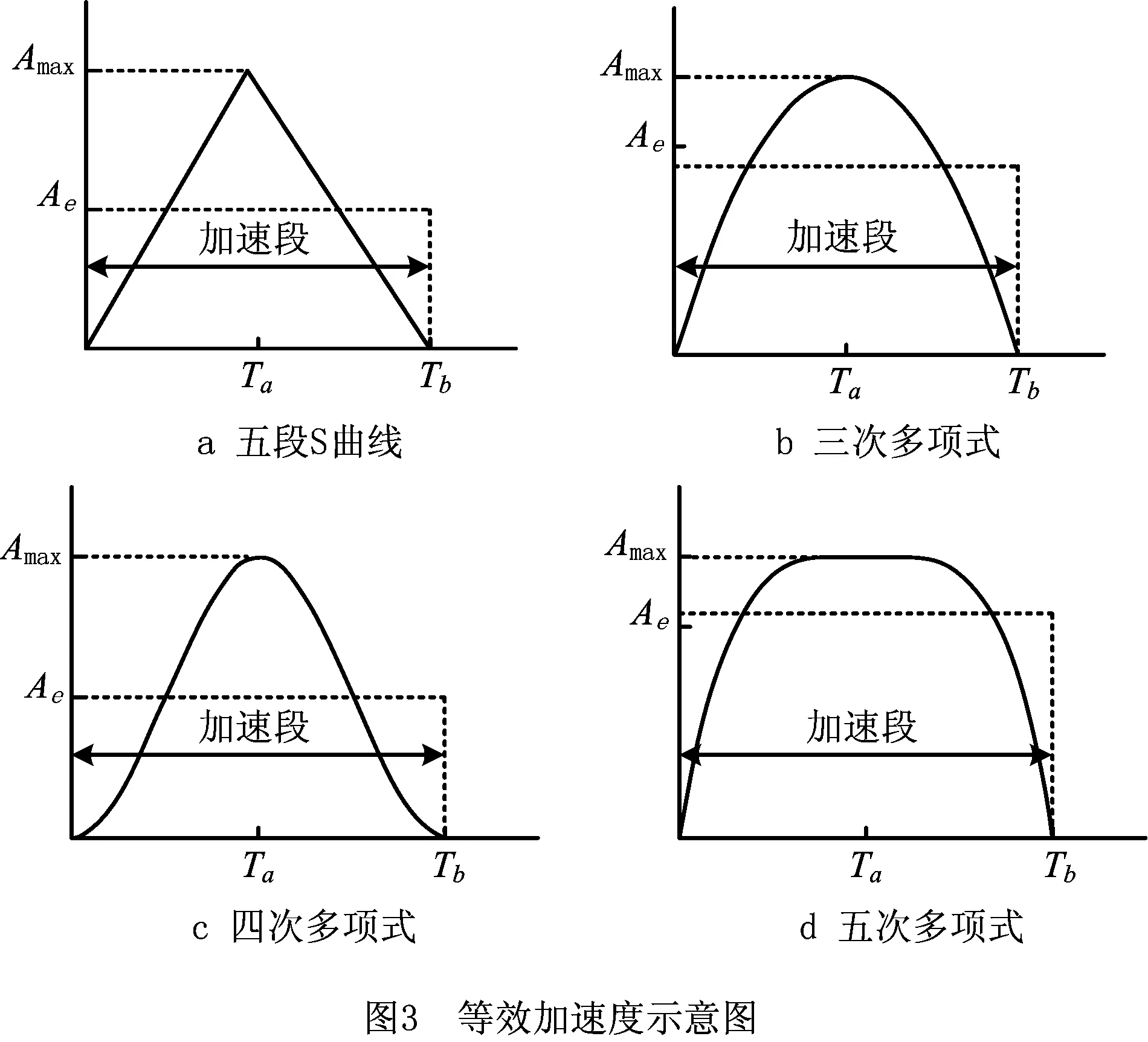
由于五次以上的加减速控制方法的计算阶次比较高，计算量非常大，因此主要就五次及五次以下的加减速控制方法进行对比分析。

除了加速过渡时间外，还需要考虑分段数、柔性、计算量等因素，具体对比情况如表1所示。

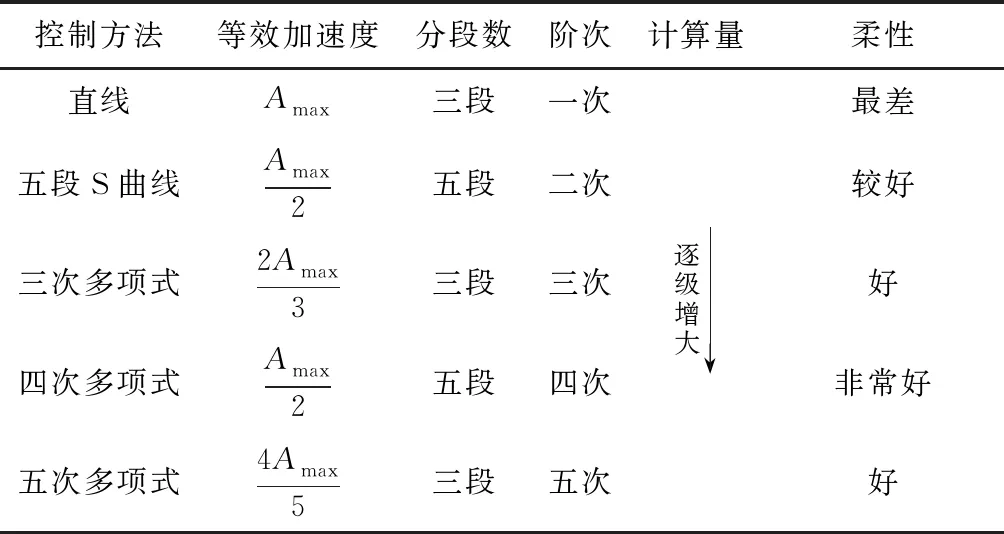
表1 加减速控制方法对比

经过综合对比分析，决定采用三次多项式加减速控制方法作为七轴龙门式自动铺丝机的速度控制方法，并采用等效加速度的方法简化其计算量。

2.2 基于等效加速度的三次多项式加减速控制方法

三次多项式加减速控制方法主要包括加速段、匀速段、减速段3部分，如图4所示，三次多项式加减速的分段数量少，但是阶次较高，为了降低计算难度，采用等效加速度简化三次多项式加减速控制方法的计算。

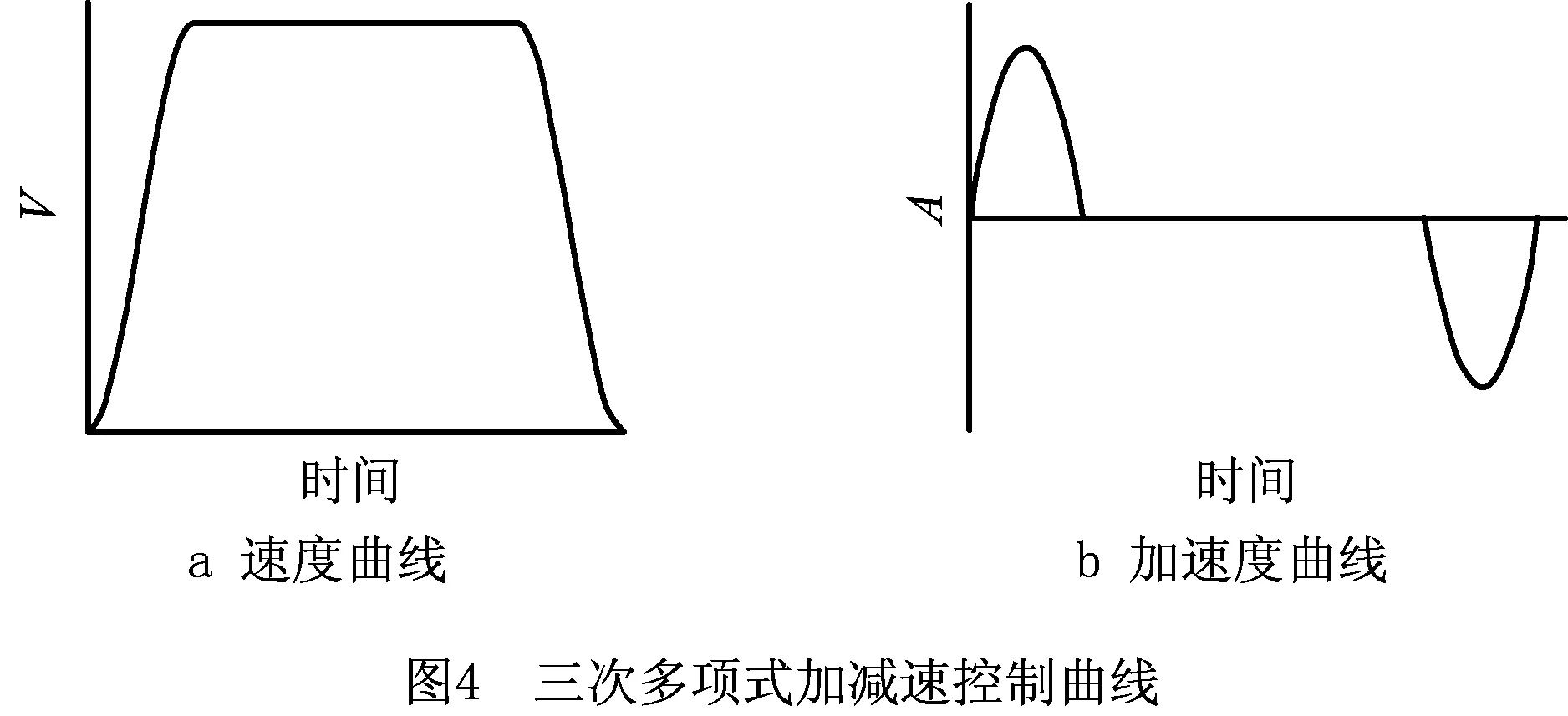
在三次多项式加减速控制方法中，设Ti(i=1,2,3)是多项式加减速控制方法中的各个时间段，即加速段0～T1，匀速段T1～T2，减速段T2～T3。

三次多项式加减速控制方法的速度函数：

V(t)=

(6)

利用积分方法计算出三次多项式加减速控制方法的位移函数：

S(t)=

(7)

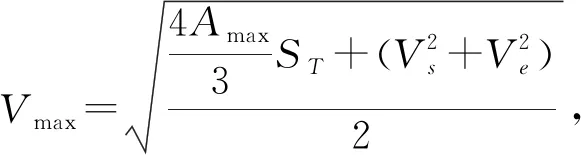
3 基于过渡曲线的插补算法分析

3.1 七轴铺丝机床运动学分析

在七轴铺丝机床插补运算过程中，需要对各轴变量和铺丝头位姿进行转换，因此根据七轴龙门式铺丝机的运动学模型[13]，计算出位姿变换矩阵。

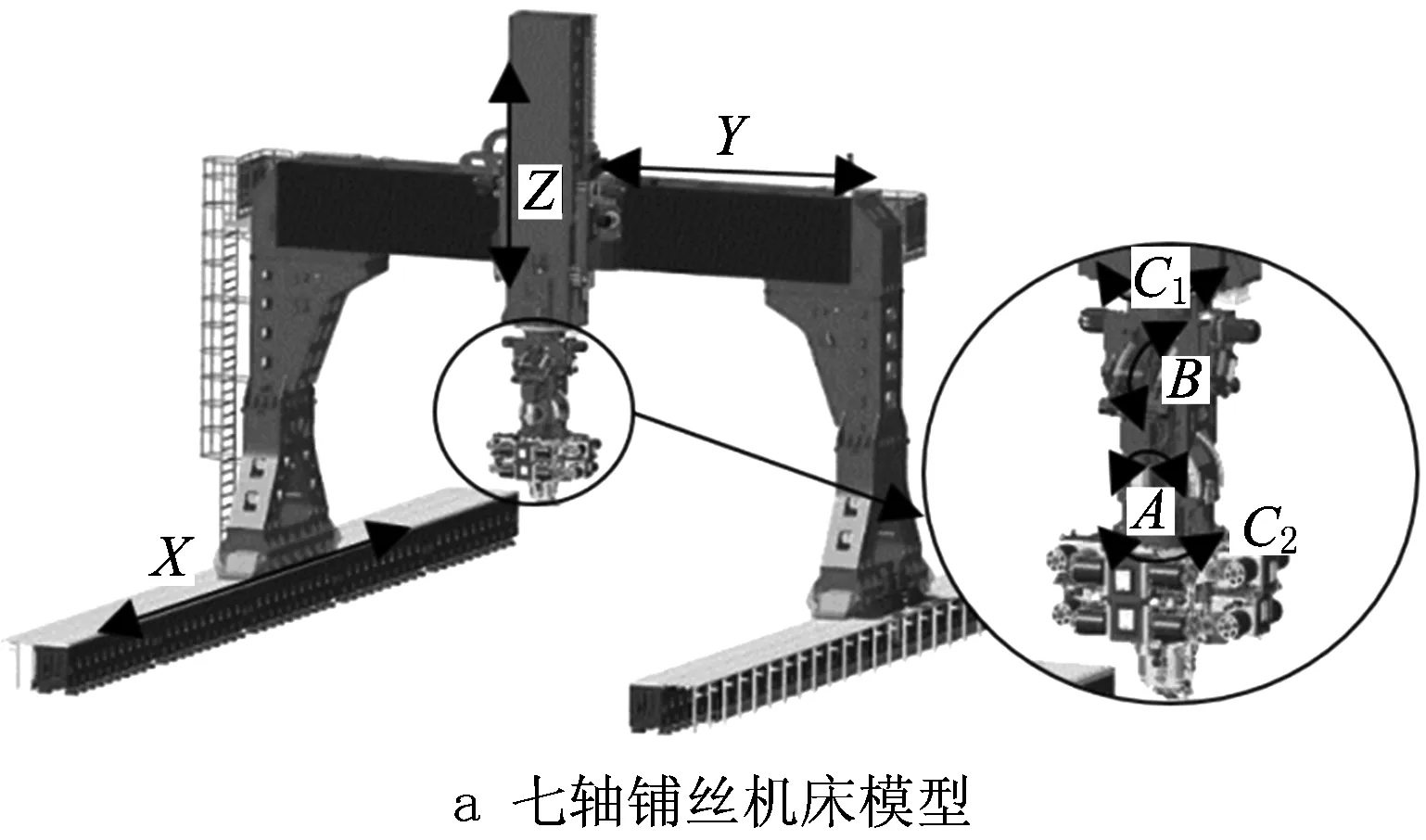
七轴龙门式铺丝机床属于七自由度串联型机床，由3个移动轴(X、Y、Z)、4个旋转轴(C1、B、A、C2)以及铺丝头组成。本文采用D-H(Denavit-Hartenberg)法[14]建立七轴铺丝机的位姿变换矩阵，但是D-H法有一个比较大的缺点：机床关节越多，需要建立的杆件坐标系就越多，位姿矩阵的计算就越复杂，而七轴龙门式铺丝机结构关节区域分明，移动轴和旋转轴可以分别进行建系，在一个直角坐标系中表示3个移动轴的运动变量，利用D-H法建立旋转轴的杆件坐标系，如图5所示，旋转轴杆件坐标系原点位于不同的位置，它们之间存在偏移参数，这样有利于修正装配制造偏差，根据D-H参数表计算出相邻坐标系之间的变换矩阵，最后按照运动链顺序相乘计算出铺丝机位姿变换矩阵T。

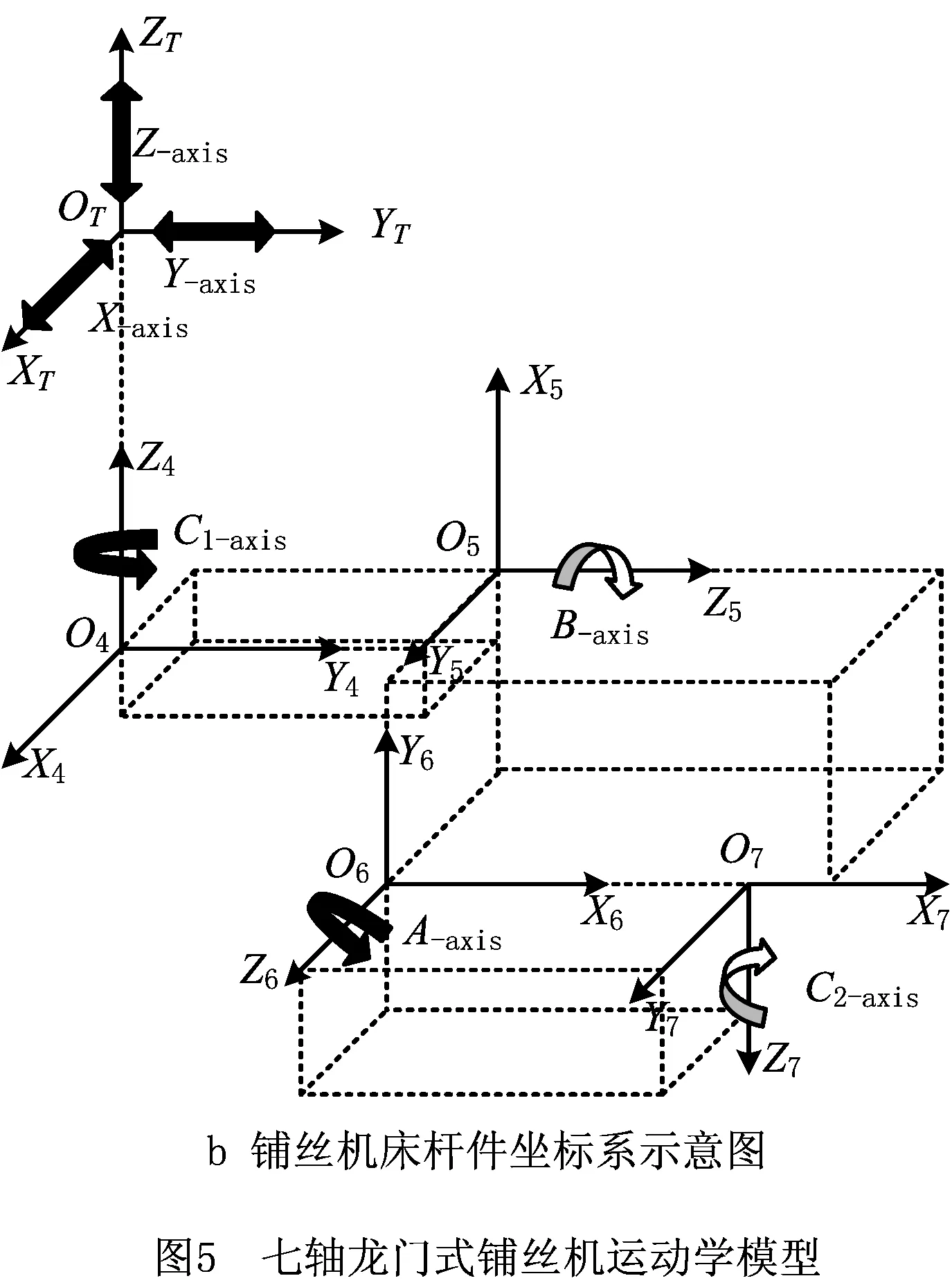
七轴龙门式铺丝机的位姿信息包括位置矢量P，切向矢量t，接近矢量a(垂直于铺放表面)，法向矢量n(垂直于切向矢量和接近矢量所在平面)，各关节变量为dx,dy,dz,θ4,θ5,θ6,θ7，已知铺丝机的D-H参数表(如表2)，表中：d5、d6、d7、a4、a5、a6为常量。

计算出的位姿变换矩阵如式(8)：

(8)

其中，利用位姿信息求各关节变量，即进行运动学反向求解时，有无穷多解，解决方法是：暂且将一个旋转轴变量看作常量，利用分离变量(矩阵求逆)的方法，计算出用该常量轴和其他关节参数表示的其他关节变量，然后根据各轴约束条件，按照最小位移法求出该常量轴中的最优解，最后求出其他关节变量。

表2 铺丝机的D-H参数

3.2 过渡曲线插补算法

七轴龙门式铺丝机床中存在3个移动轴和4个旋转轴，通过七轴铺丝机的运动学分析，其末端执行器的位置是由移动轴和旋转轴同时控制的，方向主要由旋转轴控制。过渡曲线插补方法需要同时对末端执行器的方向和位置进行插补，插补计算过程如图6所示，具体步骤如下：

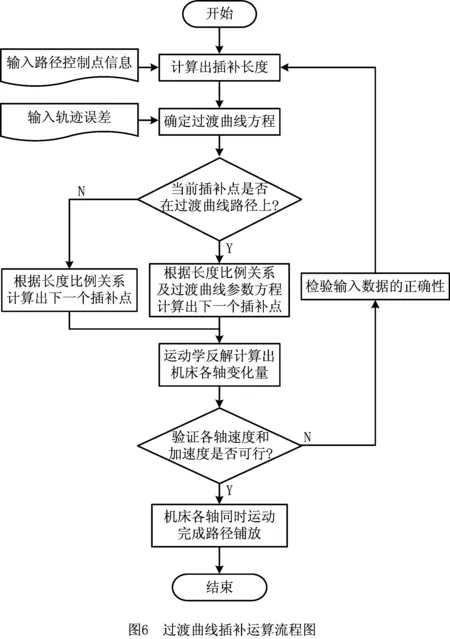
(1)已知路径控制点的位姿信息(位置矢量和方向矢量)，插补周期τ，加减速控制曲线，为保证加减速各阶段插补次数为整数，修正各阶段时间、加速度、位移量，并根据修正后的加速度曲线计算出对应的插补长度:

L=

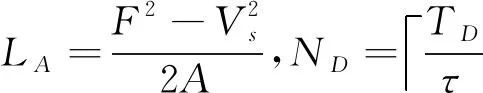
(9)

其中：L为该路径段长度；NA、NC、ND为加工路径的加速段、匀速段、减速段的插补次数；A、D为加减速控制曲线修正后的等效加速度,为向上取整。

对应的插补长度为：

Loi=Voiτ。

(10)

式中：Vi-1，Vi，Voi，Loi分别为第i插补段的开始速度、结束速度、平均速度和插补长度。

(2)直线段插补过程中，根据路径分配比确定插补点的位姿信息：

noi=cross(toi，aoi)。

(11)

式中：P1、P2为相邻的路径控制点；Poi、aoi、toi、noi为该路径段中插补点的位姿信息；cross是求两个向量的叉积。

(3)过渡曲线段的插补过程中，根据轨迹误差εmax大小，路径控制点位置矢量Pi(i=1,2,3)，求出位置过渡曲线的3个控制顶点Q0、Q1、Q2，其中过渡曲线起点和终点近似成相邻线段上的插补点(靠近拐点)，确定位置过渡曲线参数方程为：

P(u)=(1-u)3Q0+3(1-u)uQ1+

u3Q2，u∈[0,1]。

(12)

(4)根据速度曲线计算出过渡曲线起点和终点的速度Vg1，Vg2以及总的过渡时间Tg，推导出过渡曲线段的长度Sg以及各插补段的长度Ssi：

Sg=Sk+S2k+…+S1,

(13)

其中：k为过渡曲线阶段选取的采样时间，且k≤τ，采用小线段逼近的方法求过渡曲线对的长度；Vi为加减速控制的速度，Li为过渡曲线阶段速度计算的插补段长度，Lg为过渡区域内的直线段路径长度；Ssi是将速度规划中的位移等比例换算成过渡曲线中的位移。

(5)根据修正后插补段的长度Ssi、过渡曲线函数方程，计算出下一个过渡曲线段插补点位置坐标。

(6)根据过渡起点、过渡终点和拐点信息推导出接近矢量a的过渡曲线方程，并按照插补段长度确定过渡阶段插补点的接近矢量。同理，计算出过渡阶段的切向矢量t的过渡曲线方程，进而确定插补点处的切向矢量，插补点处的法向矢量n根据该点确定的接近矢量和切向矢量的叉积计算得出:

a(u)=(1-u)3R0+3(1-u)uR1+u3R2,

u∈[0,1],

t(u)=(1-u)3O0+3(1-u)uO1+u3O2,

u∈[0,1]}。

(14)

式中R0,R1,R2，O0,O1,O2分别为位置坐标Q0,Q1,Q2对应的接近矢量以及切向矢量。

(7)根据过渡阶段插补点的位姿信息，通过七轴龙门式铺丝机床的运动学矩阵计算出旋转轴和移动轴的变化量。

(8)根据各轴在插补周期内的变化量确定各轴的速度曲线，用于观察各轴速度是否在预期计算范围内，检验过渡曲线插补算法是否可行，然后进行循环，最后机床各轴同时运动完成路径的铺放。

过渡曲线插补方法采用改进的三次Bernstein-Bézier曲线作为拐点过渡曲线，能够保证轨迹切向和曲率连续，以及速度和加速度连续；通过三次曲线的参数方程来确定过渡阶段插补点的位姿信息，具有曲线阶次较低、计算简单等优势。

3.3 连续短线段插补过程

当七轴龙门式铺丝机在连续短线段的铺放路径上运动时，除了对拐点轨迹进行光顺外，还需要考虑不同插补运算阶段速度协调的问题，本文提出基于明显、平稳的位置点或速度点作为前后两插补运算阶段的协调点，保证插补运算连续平稳进行。

协调点选择方法思路如下：当下一个拐点过渡范围起点在减速段范围内时，以匀速段中间点或者速度最大点(无匀速段)为协调点，否则以下一个拐点过渡范围起点为协调点。

连续短线段插补运算过程如下：

(1)开始阶段，在插补运算框内，获取开始两个拐点相邻的4个控制点(包括两个拐点)的位姿信息，根据过渡曲线插补方法对前两段进行插补，插补到协调点处，并记录该协调点的位姿及其插补次数、速度信息，如图7a所示。

(2)中间阶段，从第2个拐点开始，插补运算框每次获取拐点后3个控制点(包括拐点)的位姿信息，从协调点开始进行插补运算，一直插补到下一个协调点处，如图7b所示。

(3)最后阶段，在最后一个拐点处，插补运算框获取该拐点后的两个控制点信息(包括拐点)，从协调点开始进行插补运算，一直插补到铺放路径结束，如图7c所示。

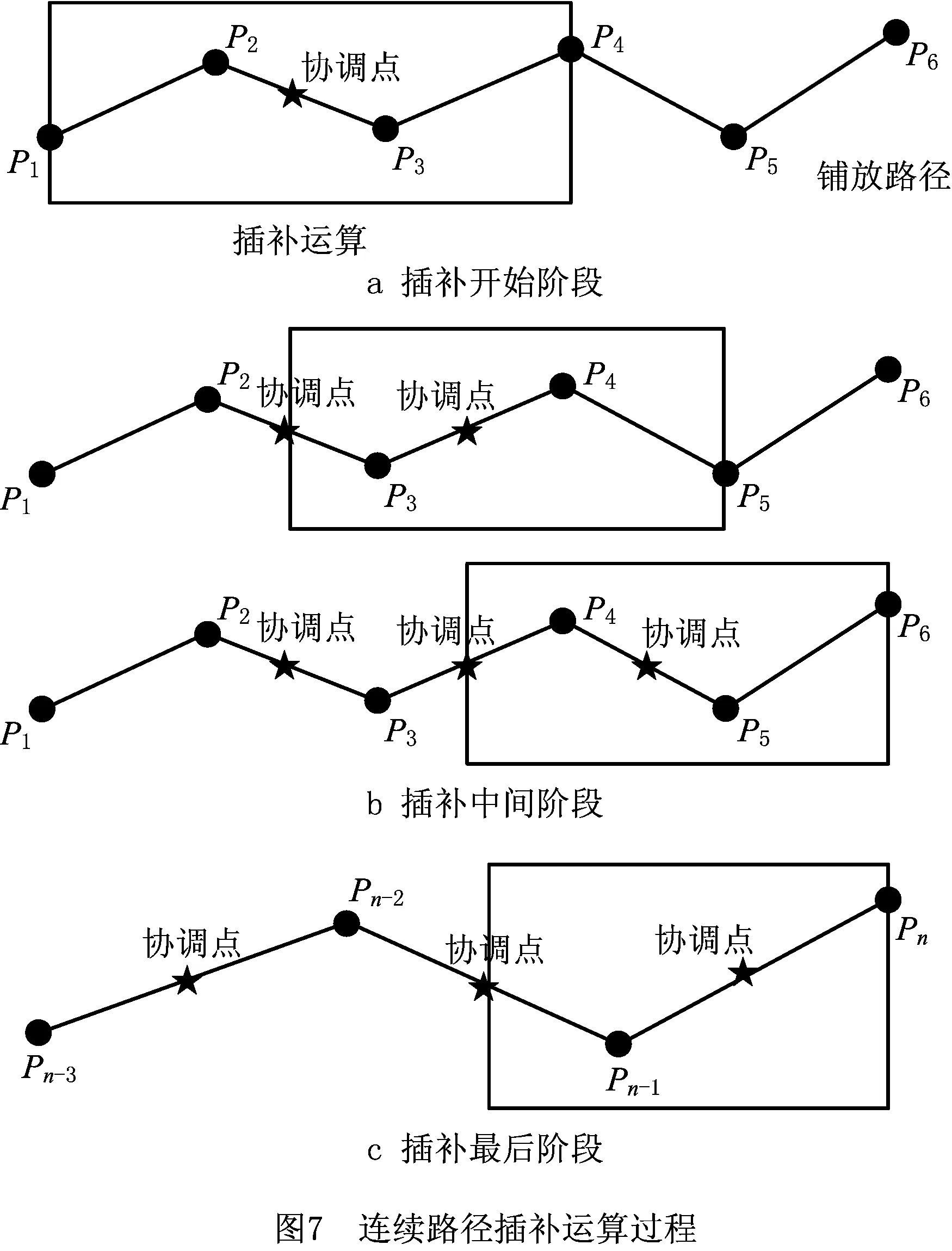
利用三次加减速控制方法中的匀速段中间点、最大速度点(无匀速段)以及拐点过渡插补算法中的过渡起点等比较特殊的位置作为协调点的选择，其优势为：①协调简单、计算方便，匀速段的规划是在加速段和减速段之后确定的，能够消除一些计算误差，且匀速段的速度基本上为指令铺放速度；②平稳性高，最高速度以及过渡范围的起点作为协调点时，主要是由路径控制点决定的，受影响的因素少。

4 算法仿真分析

为了分析基于三次Bernstein-Bézier曲线插补算法的可行性，利用MATLAB软件分别编写基于等效加速度的三次多项式加减速控制算法、插补运算算法、插补循环算法，并进行空间曲线路径的仿真运算。

已知指令铺放速度、插补周期、系统最大加速度、路径控制点信息等约束条件，当铺丝机在由连续短线段组成的铺放路径上运动时，为了解拐点处存在的速度不连续问题，首先通过MATLAB软件对相邻直线路径进行仿真，相邻直线路径控制点信息如表3所示，得到拐点进行处理之前的各轴速度图像，如图8所示。其中，七轴龙门式铺丝机床是通过优化其中一个轴而对其他轴进行控制。本文是对C2轴进行优化的，因此在研究各轴速度时，只对其余6个轴的速度进行计算。

表3 路径信息

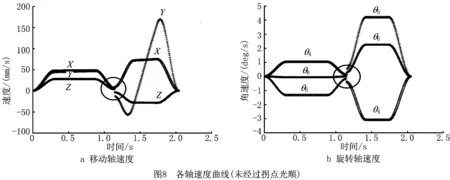
可以看出，在相邻线段拐点处，由于线段方向不同，各轴的直线分配比不同，导致各轴速度在拐点处产生间断跳跃，造成机床产生超程、振荡等问题，降低了机床的加工性能。

曲线形路径是七轴铺丝机中常见的铺放路径，或者是铺放路径的组成部分，因此以曲线形路径为例，进行连续短线段插补过程的仿真计算分析。利用浙江大学邢纪鹏[15]优化后的目标路径进行插补研究，该路径由10个控制点控制，路径控制点信息如表4所示，路径控制点信息包括位置坐标、接近矢量、切向矢量、法向矢量，各控制点之间采用连续短线段的轨迹描述方式，如图9所示。

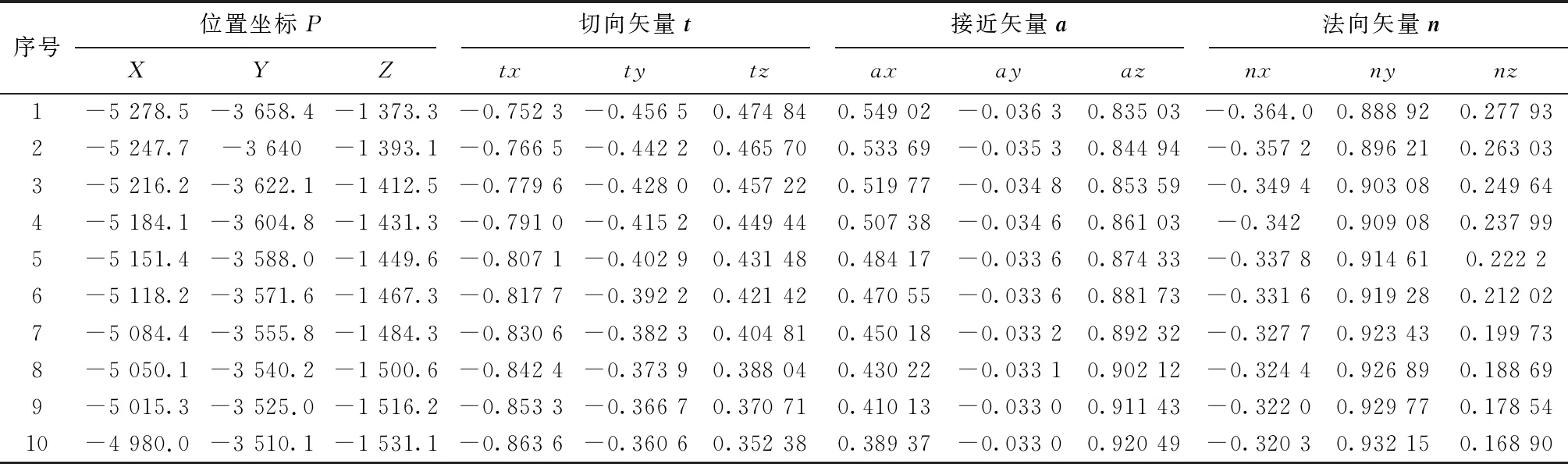
表4 曲线形路径控制点

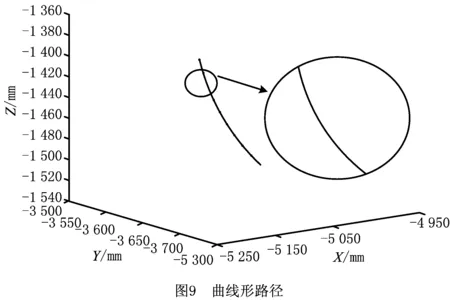
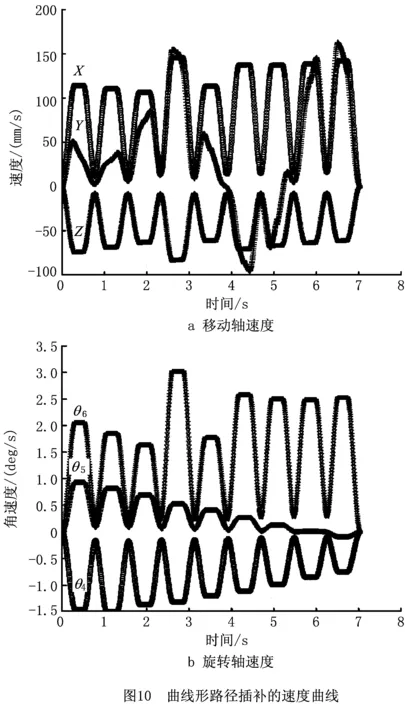
通过MATLAB仿真计算出过渡曲线插补算法在曲线形路径上的运动速度和加速度情况，如图10和图11所示，过渡曲线插补算法是在柔性加减速控制方法的基础上，对“直线段+过渡曲线段”铺放路径进行插补，并通过标注协调点的方法保证各插补运算段之间速度和加速度连续。仿真结果表明，基于三次Bernstein-Bézier曲线过渡的连续短线段插补算法能够很好地完成曲线形路径铺放。

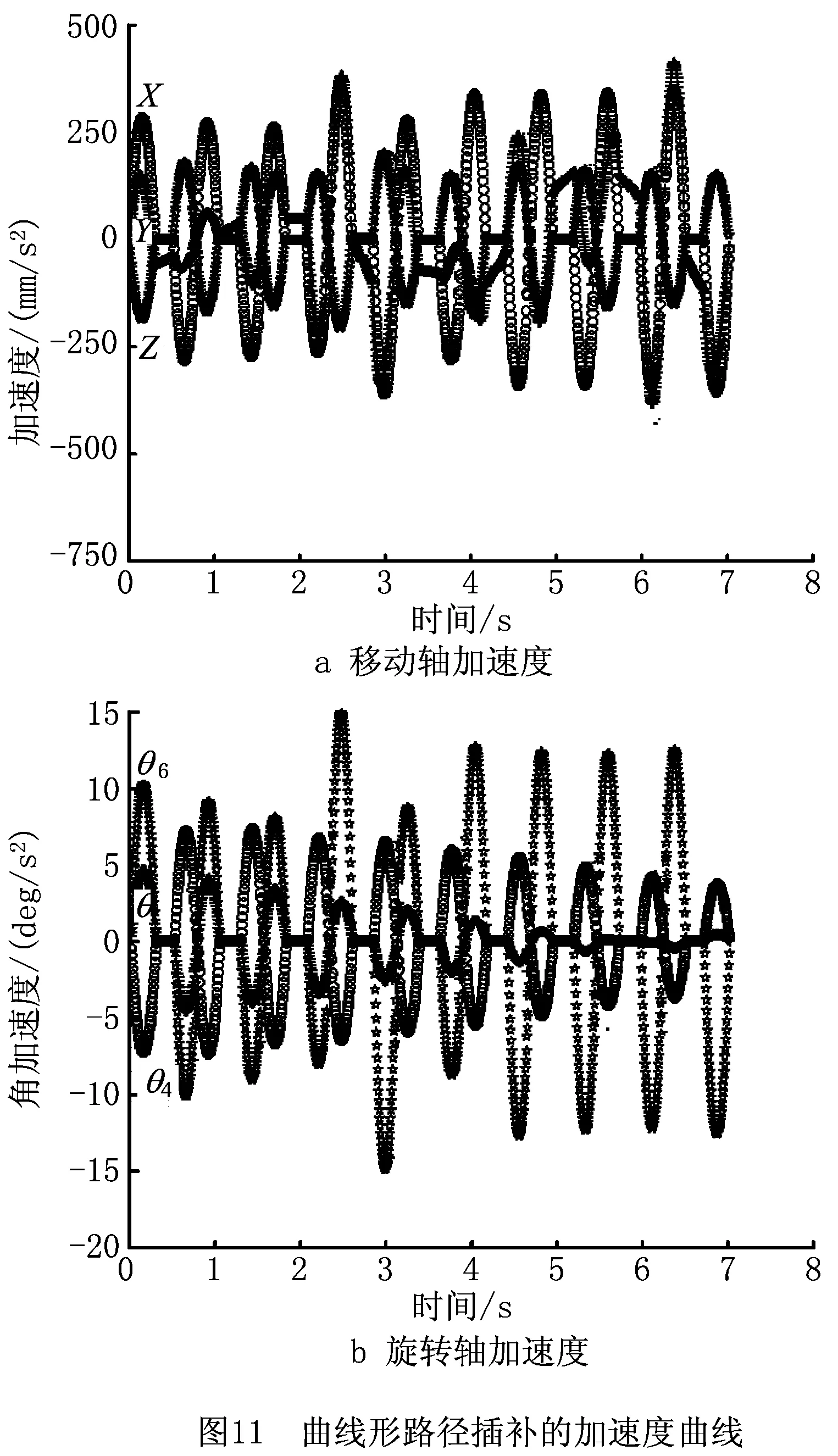
在插补方法中，采用改进的三次Bernstein-Bézier曲线进行过渡，通过速度和加速度图像可以看出，该方法能够保证机床平滑的运动，与其他方法相比，本身也具有一定的优势，如表5所示。

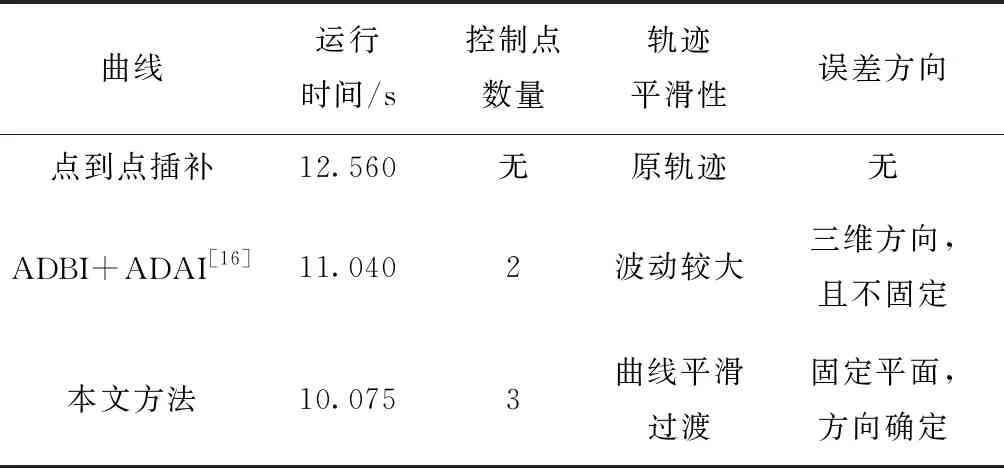
表5 三种插补过渡方法比较

其中，点到点插补方法是将机床在拐点处的速度设为零，从一个控制点运动到另一个控制点，机床频繁起停，对机床本身具有相当大的损害，且效率大大降低；插补前加减速(Acc/Dec before Interpolation, ADBI)和插补后加减速(Acc/Dec after Interpolation, ADAI)方法是通过保证各轴速度连续的方法保证拐点光顺过渡，但最后的过渡路径形状不固定，且在三维空间内波动；本文提出的方法，相对运行时间较短，且最后的过渡路径固定在相邻线段间的平面上，具有一定的实用价值。

5 结束语

根据加速时间、计算量、柔性等方面综合分析多种加减速控制方法，确定基于等效加速度的三次多项式加减速作为七轴龙门式铺丝机的速度控制方法。三次多项式加减速控制方法具有较高的柔性，且可以利用等效加速度简化计算，能够保证七轴铺丝机以较好的性能达到指令铺放速度，从而提高加工效率。

改进三次Bernstein-Bézier曲线，仅通过3个控制顶点定义一段曲线，利用曲线性质和轨迹误差计算出曲线控制顶点的位置，该曲线能够保证相邻直线段切向和曲率连续过渡；提出基于改进的三次Bernstein-Bézier曲线插补算法，首先分别利用三次Bernstein-Bézier曲线对位置向量、姿态向量进行过渡；然后在柔性加减速控制方法的基础上，对“直线段+过渡曲线段”铺放路径进行插补运算；最后在连续插补过程中，提出采用标注协调点的方法保证前后段速度连续，经过拐点光顺、速度协调之后，机床能够平稳准确地完成路径铺放。

本文的研究工作主要基于理论分析、算法设计和仿真计算，今后的研究将考虑实际铺放过程中出现的多种情况，以期实现更加完备的运动控制方法。