多层非均匀径向复合储层压力动态特征

高 敏，段 蕾，史文洋，颜家伟，陆科杰

(1.中国石油股份有限公司长庆油田分公司第四采油厂，宁夏银川 750006；2.中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249；3.中国石油股份有限公司长庆油田分公司第三采油厂，宁夏银川 750006；4.中海油能源发展股份有限公司工程技术分公司，天津 300452)

随着石油勘探开发理论与技术的发展，越来越多的复杂油气储层被发现并进行商业开采。储层的描述表征以及生产过程中的储层再认识一直是矿场比较关心的问题。在非均质储层渗流的刻画方面，层状油藏模型和复合油藏模型是最常用的两种经典模型。Gao[1]针对多层油藏首次提出了存在层间越流的半透壁渗流模型，Bourdet[2]建立了经典的无越流层状储层压力模型。文献[3-9]研究了多层合采油气藏的储层压力和渗流特征，建立了考虑层间越流和无层间越流的压力响应模型，奠定和发展了多层油藏渗流与试井方法理论。文献[10-15]对多层油气藏渗流模型进行了系统的综述，总结对比了考虑复合特征的多层储层渗流模型的求解方法以及内外边界条件等，最后给出了多层径向复合模型压力解的结构和求解方法。

现存的多层径向复合渗流模型中，只针对较少层数(2～3层)的模型进行各层复合半径不相等的处理。严格意义上说，缺少真正的多层非均匀径向复合储层渗流模型。为了明确纵向非均匀复合储层的压力响应特征，分析非均匀复合半径对压力响应的影响规律，本文建立了考虑各类非均匀复合半分布的多层储层压力响应模型，进一步完善和补充了多层复合储层渗流理论。

1 模型的建立与求解

1.1 物理模型

纵向非均匀径向复合模型如图1所示，假设储层为n层，各层均为水平等厚的储层；第j(j=1,…,n)层的流体黏度、储层综合压缩系数、厚度分别为μj、Ctj、hj；第j层内区渗透率、孔隙度、外边界分别为k1j、Φ1j、rcj，第j层外区渗透率、孔隙度、外边界分别为k2j、Φ2j、re；生产井位于储层中心，以定产q进行生产；开井前储层压力处处相等，储层内充满微可压缩流体；开井后各层流体满足达西定律向井底径向流动，且层间无越流。

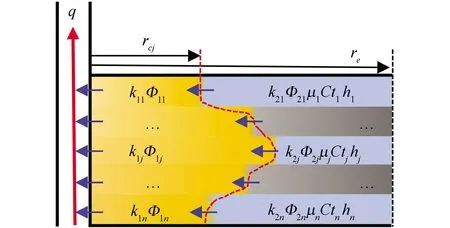
图1 纵向非均匀径向复合模型示意图

以井轴为中心，各层流体向井底流动时各层储层内压力p的分布满足下述定解问题。

(1)

pij|t=0=pr

(2)

(3)

p1j|rD=1=pw

(4)

(5)

p1j|r=rcj=p2j|r=rcj

(6)

p2j|r→∞=pr

(7)

1.2 数学模型

定义无量纲变量：

rD=r/rw

(8)

(9)

(10)

(11)

pijD=2π(kh/μ)a(pr-pij)/q

(12)

χij=(kh/μ)ij/(kh/μ)a

(13)

ωij=(ΦCth)ij/(ΦCth)a

(14)

Mj=(kh/μ)1j/(kh/μ)2j

(15)

Dj=(ΦCth)1j/(ΦCth)2j

(16)

式中χ——流动系数比，无量纲；

ω——储容系数比，无量纲；

M——渗透比，无量纲；

D——储能比，无量纲。

拉氏空间下对应的由无量纲渗流方程和边界条件构成的数学模型为：

(17)

式中u——拉氏空间变量；

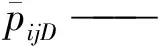
1.3 模型求解

内区渗流方程解可用Bessel函数表示：

(18)

式中A——待求系数，无量纲；

Ia——a阶第一类修正Bessel函数，无量纲；

B——待求系数，无量纲；

Ka——a阶第二类修正Bessel函数，无量纲。

外区为无限大边界，渗流方程解为：

(19)

式(18)和(19)中一共有3n个未知系数，根据内边界的1个产量方程、n-1个压力方程，层交界面n个流量连续方程、n个压力连续方程，得到3n×3n线性方程组：

(20)

式(20)中，aj=χjσ1I1(σ1)，bj=-χjσ1K1(σ1)，cj=I0(σ1)，dj=K0(σ1)，ej=σ1I1(σ1rcDj)，fj=-σ1K1(σ1rcDj)，gj=σ2K1(σ2rcDj)/Mj，hj=I0(σ1rcDj)，mj=K0(σ1rcDj)，oj=-K0(σ2rcDj)。

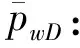
(21)

利用Shetfesh数值反演方法得到实空间下无量纲井底压力的解pwD。

2 模型典型曲线特征

以n=10为例，图2为模型参数弱化后的井底压力和压力导数曲线。模型的参数弱化说明非均匀复合模型是纵向均质复合模型的泛化，纵向非均匀复合模型相比于单层复合模型具有更广的适用范围。从压力和压力导数典型曲线上可以看出纵向非均匀复合储层存在3个明显的流动特征。

图2 纵向非均匀复合模型典型曲线

(1)内区径向流阶段：在纵向均质的条件下，内区径向流阶段的压力导数l为0.5；在纵向非均质的条件下，内区径向流阶段的压力导数仍为一段水平线，压力导数值l=0.5/n。

(2)过渡流阶段：由于外区储层物性变差(M=D>1)，因此压力导数出现上升。当外区储层物性远远差于内区储层物性时(M=D=100)，压力和压力导数曲线出现类似封闭边界的特征，压力和压力导数斜率m=1。

(3)外区径向流阶段：当压力传播到外区更远的储层时，外区流体径向地流进内区，流动表现为径向流动阶段，压力导数值L=M·l。

3 敏感性分析

3.1 层数

图3揭示了纵向非均匀复合模型中层数n对井底压力响应的影响规律。如图3所示：n=2时，取rcD=100，内区径向流阶段的压力导数值l1=0.25；n=5时，取rcD=200，内区径向流阶段的压力导数值l2=0.1；n=10时，取rcD=400，内区径向流阶段的压力导数值l3=0.05。即内区径向流阶段的压力导数值l=0.5/n。

图3 层数敏感性分析

3.2 非均匀复合半径

为了分析多层非均匀复合半径对井底压力响应的影响，设计了两类纵向非均匀内区半径。第一类是直线类内区半径，用来刻画断层、地垒、地堑式复合储层[12-13]；第二类是双曲类内区半径，用来模拟碳酸盐岩填充溶洞或者砂岩透镜状、块状岩性复合储层[20-23]。

3.2.1 直线类复合半径

图4显示了2种直线倾覆内区半径与3个均匀内区半径的压力响应曲线。图中所示倾覆类内区半径具有3种性质。①对称性：两种直线倾覆类内区半径对应的压力响应曲线完全重合；②有界性：直线倾覆类内区半径压力响应曲线介于最小内区半径和最大内区半径对应的压力响应曲线之间；③中值性：存在一个内区中值半径的压力响应曲线与实际直线倾覆类内区压力响应曲线完全重合，且内区中值半径不等于内区均值半径。内区中值半径的取值遵守等效渗流空间法则：非均匀复合储层的渗流空间是复杂的，可以用一个规则的渗流空间来替代它，使两者具有相同的压力响应特征。等效渗流空间可以解释试井多解性：无论多么复杂的储层，总能找到一个或多个等效渗流空间。由于均值半径不一定等于中值半径，因此，慎用均值半径处理纵向非均匀径向复合类储层。

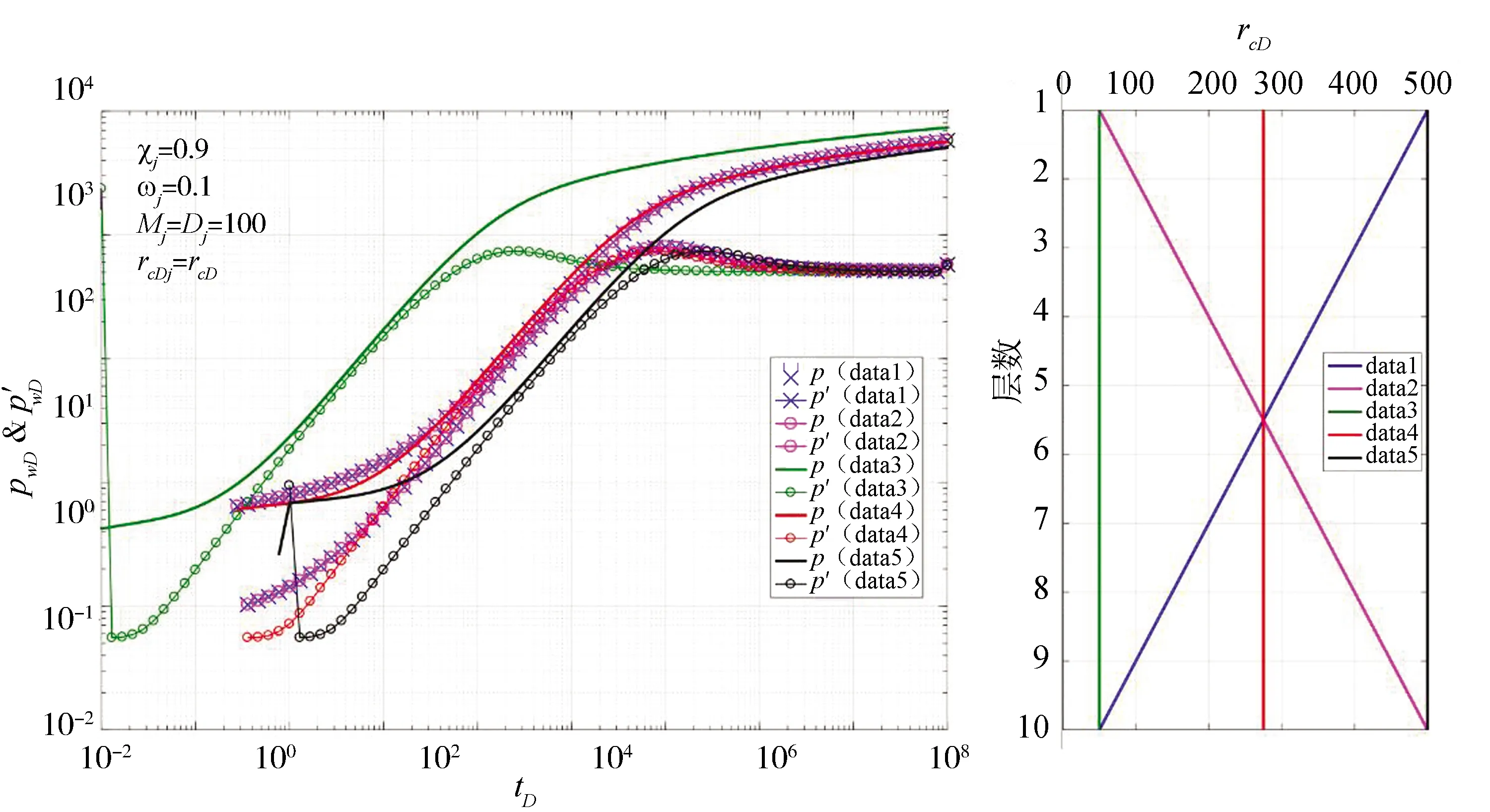
图4 直线类内区半径敏感性分析

3.2.2 双曲类复合半径

图5表示抛物线型内区前缘对压力响应的影响规律：参与径向复合渗流的层数逐渐减少，内区径向流阶段的压力导数值按照l=0.5/n的规律逐渐增大；根据等效渗流体积的概念，内区中值半径逐渐减小，过渡流出现的时间靠前。图5中①和②内区前缘具有相同的压力响应曲线，说明两者具有相同的等效渗流体积。如果储层厚度很大，或内区体积不是很大，则通过井底压力响应曲线难以识别内区复合体积的纵向位置，如图6所示。

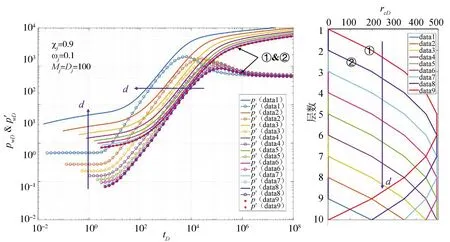
图5 抛物线型内区半径敏感性分析

图6 内区体积纵向位置敏感性分析

4 实例分析

图7表示B2井于2006年9月进行的一次压力恢复的测试结果。结合B2井的储层构造来看，“三边封闭+一边定压”矩形外边界模型是最符合B2井实际储层特征的[21]；如果不结合储层特征，仅针对B2井的压恢数据就有5种外边界解释模型能较好地拟合，其中3个矩形边界模型解释的最近封闭边界分别为101 m、115 m、140 m，2个径向复合得到的内区半径值分别为120 m、122 m(表1)。

表1 各类拟合模型的边界类型及参数

图7 B2井双对数曲线及各类边界拟合对比图

3类矩形边界得到的最近封闭边界平均值为118.67 m，与2个复合半径都十分接近。根据等效渗流体积概念可以认为：B2井对应的等效渗流体为半径约为120 m的圆柱体，渗流范围超过120 m将会收到储层外边界的干扰和影响。等效渗流体积的概念可以用来简化并解释实际复杂储层，但是容易丢失真实和精细的储层特征。利用等效渗流体积可以解释试井的多解性，但是试井的多解性问题需要结合地质资料和现场认知消除。

5 结论

(1)纵向非均匀径向复合渗流储层存在3个流动阶段：内区径向流、过渡流、外区径向流。内区径向流阶段的压力导数值l与参与径向复合渗流的层数n有关：l=0.5/n；过渡流出现的时间与内区中值半径有关；外区径向流的压力导数值L与内区流度比M有关：L=M·l。

(2)纵向非均匀径向复合半径对压力响应的影响规律具有：①对称性，具有对称的两个非均匀径向复合储层具有相同的压力响应；②有界性，非均匀径向复合储层压力响应曲线位于最小复合半径和最大复合半径对应的压力响应曲线之间；③中值性，存在一个纵向均匀的内区半径，其对应的压力响应与非均匀径向复合半径对应的井底压力响应相同。

(3)内区中值半径代替非均匀径向复合半径引起的压力响应误差远小于均值半径代替非均匀径向复合半径引起的误差，中值半径可以根据等效渗流体积法则得到；内区均值半径不一定等于内区中值半径，慎用均值半径替代纵向非均匀复合半径。

(4)等效渗流体积法则可以解释试井的多解性。可以用等效中值半径处理纵向非均匀类复杂储层，解释其井底压力响应行为，但是等效中值半径的处理方法不能够准确精细地描述复杂储层的局部特征。