含裂纹功能梯度材料Timoshenko梁的非线性静力分析
马明辉 郑玉芳 陈昌萍





摘 要:利用转动弹簧模型模拟裂纹,给出由裂纹引起的局部柔度表达式。基于一阶剪切变形理论和Von Karman非线性理论建立含裂纹功能梯度材料Timoshenko梁的非线性力学模型,采用Hamilton原理推导了含裂纹功能梯度材料Timoshenko梁的非线性平衡微分方程,利用伽辽金方法对该非线性偏微分方程组进行求解。数值计算中分析了跨高比、裂纹位置、裂纹深度和弹性模量比值等因素对含裂纹FGM梁非线性静力响应的影响。
关键词:功能梯度材料梁;一阶剪切变形理论;Von Karman非线性理论;伽辽金法
中图分类号:TU311 文献标志码:A
基金项目:国家自然科学基金资助项目(51778551)
功能梯度材料(functionally graded material,FGM)是两种或多种材料复合且成分和结构呈连续梯度变化的一种新型复合材料[1],其材料组分能够沿一定的空间方向连续变化,可以通过不同的组成方式和梯度变化以满足特定工况的使用需求,在航空航天、核能和机械等工业领域得到广泛应用。任何材料包括FGM在实际使用过程中都会出现局部微观裂纹,在工程结构中裂纹损伤是普遍存在的。结构中裂纹的存在将会影响结构的刚度、强度以及质量等特性。再者,梁构件广泛应用于工程实际,所以对含裂纹功能梯度材料梁力学行为的研究具有十分重要的意义。
马连生等[2]基于多种梁理论,结合Hamilton原理等方法对FGM梁进行研究,讨论了梁的几何参数、边界条件、外载荷以及材料梯度参数对FGM梁的非线性静态响应问题的影响。李华东等[3]基于应力函数法,对梯形分布载荷作用下FGM简支梁弯曲问题的解析解进行了研究。REDDY等[4]基于Euler-Bernoulli和Timoshenko梁理论,分析了轴向变形和弯曲变形耦合的FGM梁的静力弯曲问题。NIKNAM等[5]采用伽辽金方法和广义微分求积法研究了不同热载荷和机械载荷对具有一般边界条件的渐变FGM梁非线性静力弯曲性能的影响。魏东等[6]基于Euler-Bernoulli和Timoshenko梁理论,建立了一种求解含裂纹FGM梁的屈曲载荷计算方法。邓昊等[7]采用扭转弹簧模型对裂纹进行模拟,基于动力学方法建立了功能梯度Timoshenko梁的表面裂纹传递矩阵,结合增广拉格朗日算法和差分进化算法对结构进行损伤识别。YANG等[8]基于欧拉梁理论和转动弹簧模型,对含裂纹FGM梁进行了数值分析,研究了裂纹数量、裂纹位置、材料属性、细長比和支撑边界对梁弯曲振动和屈曲的影响。TANG等[9]提出了一种新的双向功能梯度材料欧拉梁模型来研究其非线性自由振动行为。RAJASEKARAN等[10]采用Euler-Bernoulli梁理论和一种新的有限元方法对双向功能梯度单裂纹/多裂纹梁的动力特性进行了研究。SONG等[11]基于一阶剪切变形理论,研究了功能梯度多层石墨烯增强复合材料梁的线性自由振动和弹性屈曲行为。LIEN等[12]基于一阶剪切变形理论,结合裂纹旋转弹簧模型,对功能梯度材料多裂纹梁的线性自由振动问题进行研究。KOU等[13]利用无网格边界域积分方程法,研究含张开裂纹功能梯度材料梁的自由振动问题。从研究现状来看,考虑几何非线性以及一阶剪切变形理论的FGM裂纹梁的研究成果相对较少。
本文利用转动弹簧模型模拟裂纹,基于一阶剪切变形理论和Von Karman非线性理论建立功能梯度材料Timoshenko梁的非线性力学模型,采用Hamilton变分原理推导功能梯度材料Timoshenko梁的非线性平衡微分方程。通过伽辽金方法对该非线性偏微分方程组进行求解,分析跨高比、裂纹位置、裂纹深度和弹性模量比等因素对含裂纹FGM梁非线性静力响应的影响,并与相应的文献结果进行对比。
5 结语
本文研究了含裂纹功能梯度材料Timoshenko梁的非线性静力响应。通过一阶剪切变形理论和Von Karman非线性理论建立了含裂纹功能梯度材料Timoshenko梁的非线性力学模型,分析了跨高比、裂纹位置、裂纹深度和弹性模量比值对FGM梁的挠度曲线的影响。数值结果表明:
1)裂纹的存在会导致结构刚度减小,在其他条件一定的情况下,有裂纹的FGM梁的挠度明显要比无裂纹的FGM梁的挠度大。由此可见,裂纹会降低功能梯度材料梁的刚度和承载力等力学特性,在工程设计中应考虑裂纹损伤对FGM结构的影响。
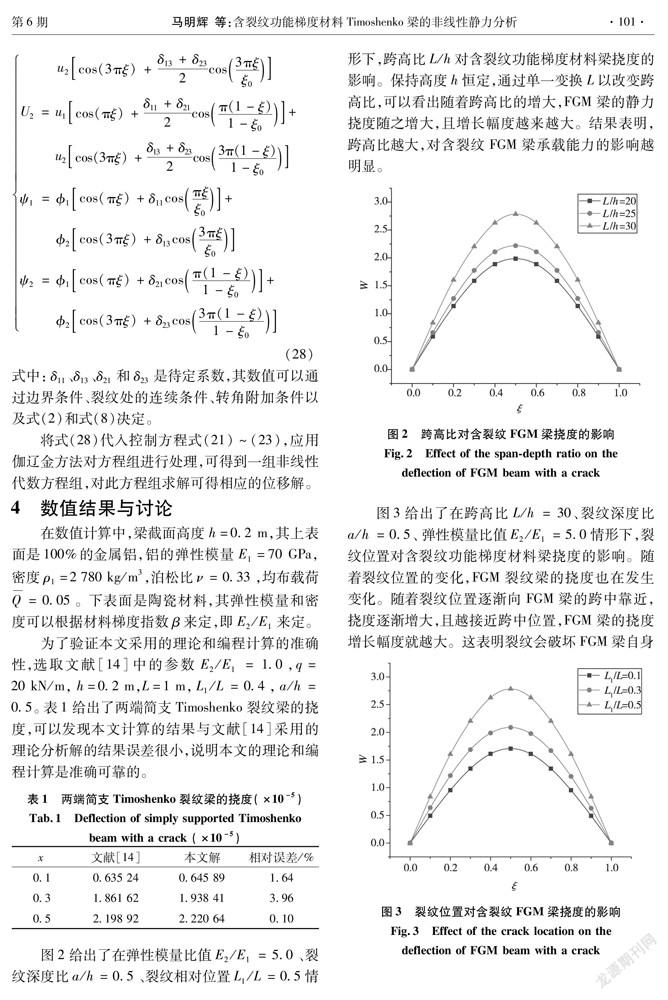
2)随着跨高比、裂纹深度的增大,裂纹位置逐渐向FGM梁的跨中靠近,FGM梁的静力挠度随之增大,且增长幅度越来越大。
3)当其他条件保持不变时,FGM梁的挠度随着弹性模量比值的增大而逐渐减小,可以理解为当弹性模量比值增大时,FGM梁结构的整体刚度增大,其挠度随之减小。参考文献:
[1]韩杰才, 徐丽, 王保林, 等. 梯度功能材料的研究进展及展望[J]. 固体火箭技术, 2004(3): 207-215.
[2] 马连生, 张璐. 面内热载荷作用下功能梯度梁热过屈曲精确解[J]. 兰州理工大学学报, 2015, 41(1): 164-167.
[3] 李华东, 梅志远, 朱锡, 等. 梯形载荷作用下功能梯度简支梁弯曲的解析解[J]. 船舶力学, 2015, 19(Z1): 95-105.
[4] REDDY J N, NAMPALLY P. A dual mesh finite domain method for the analysis of functionally graded beams[J]. Composite Structures, 2020, 251. DOI: 10.1016/J.COMPSTRUCT.2020.112648.
[5] NIKNAM H, FALLAH A, AGHDAM M M. Nonlinear bending of functionally graded tapered beams subjected to thermal and mechanical loading[J]. International Journal of Non-Linear Mechanics, 2014, 65: 141-147.
[6] 魏东, 刘应华. 含裂纹功能梯度Euler-Bernoulli梁和Timoshenko梁的屈曲载荷计算与分析[J]. 复合材料学报, 2010, 27(4): 124-130.
[7] 邓昊, 程伟. 一种功能梯度Timoshenko梁的损伤识别方法[J]. 北京航空航天大学学报, 2016, 42(10): 2214-2221.
[8] YANG J, CHEN Y. Free vibration and buckling analyses of functionally graded beams with edge cracks[J]. Composite Structures, 2008, 83(1): 48-60.
[9] TANG Y, LV X F, YANG T Z. Bi-directional functionally graded beams: asymmetric modes and nonlinear free vibration[J]. Composites Part B, 2019, 156: 319-331.
[10]RAJASEKARAN S, KHANIKI H B. Free vibration analysis of bi-directional functionally graded single/multi-cracked beams[J]. International Journal of Mechanical Sciences, 2018, 144: 341-356.
[11]SONG M, GONG Y, YANG J, et al. Free vibration and buckling analyses of edge-cracked functionally graded multilayer graphene nanoplatelet-reinforced composite beams resting on an elastic foundation[J]. Journal of Sound and Vibration, 2019, 458: 89-108.
[12]LIEN T, NGO T D, NGUYEN T K. A new form of frequency equation for functionally graded timoshenko beams with arbitrary number of open transverse cracks[J]. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering, 2019, 43(1): 235-250.
[13]KOU K P, YANG Y. A meshfree boundary-domain integral equation method for free vibration analysis of the functionally graded beams with open edged cracks[J]. Composites, 2019, 156(1): 303-309.
[14] 馮新, 刘彦辉, 周晶. 一种Timoshenko裂纹梁的静力挠度分析方法[J]. 防灾减灾工程学报, 2009, 29(6): 652-657.
(责任编辑:曾 晶)
作者简介:马明辉 (1996—),男,在读硕士,研究方向:结构静动力学分析,E-mail: minghui_ma@163.com.
通讯作者:郑玉芳,E-mail: zheng_yufang@163.com.
Nonlinear Static Analysis of Cracked Functionally
Graded Material Timoshenko Beam
MA Minghui ZHENG Yufang CHEN Changping
(1. College of Civil Engineering, Fuzhou University, Fuzhou 350108, China; 2. Department of Civil Engineering
and Architecture, Xiamen University of Technology, Xiamen 361024, China)
Abstract: The rotating spring model is used to simulate the crack, and the local flexibility expression caused by the crack is given. Based on the first-order shear deformation theory and Von Karman nonlinear theory, the nonlinear model of the cracked functionally graded material Timoshenko beam is established. The Hamilton principle is used to derive the nonlinear balanced differential equation of the cracked functionally graded material Timoshenko beam. The system of differential equations is solved by the Galerkin method. In the numerical calculation, the effects of the factors such as span-depth ratio, crack location, crack depth and elastic modulus ratio on the nonlinear static response of cracked FGM beams are analyzed.
Key words: functionally graded material beam; first-order shear deformation theory; Von Karman nonlinear theory; Galerkin method

