基于回路分析法的含环网配电网改进潮流算法
顾思,孙晓,马畅,陈静
基于回路分析法的含环网配电网改进潮流算法
顾思1,孙晓1,马畅2,陈静2
(1.南京工程学院电力工程学院,江苏省 南京市 211167;2.新疆阜康抽水蓄能有限公司,新疆维吾尔自治区 阜康市 830011)
为了提高配电网消纳清洁能源能力,进一步提升配电网供电可靠性,配电网合环运行受到越来越多的关注。针对传统前推回代法处理环网潮流时出现不收敛情况,结合回路分析法与前推回代法,提出一种含环网配电网改进潮流算法。通过分解支路电流,对环网分裂点电流进行补偿,改变其不收敛现象,并且通过Matlab进行数据仿真,验证了此算法的有效性和精确性。
配电网;分布式发电;合环运行;回路分析法;前推回代法
0 引言
随着主动配电网的发展以及分布式发电技术的大规模应用,传统辐射型配电网由于无法满足分布式电源(distributed generation,DG)大规模友好接入,受限于单条馈线容量和某些分布式能源的“逆调峰”特性,消纳清洁能源的能力有限[1],因此,研究含环网情况下的配电网潮流算法非常必要[2-5]。
目前,针对环网的潮流算法研究主要集中在改进牛顿法、隐Zbus高斯法以及回路阻抗法。文献[6]提出源于牛顿法的改进方法来处理含DG的短暂环网潮流计算不收敛问题,其算法虽然处理环网能力强,但是计算复杂度高,收敛慢;文 献[7]通过在改进前推回代法中添加松弛因子,改变其不收敛的现象,但本质上仍然是辐射网计算方法,计算精度低;文献[8-9]主要从DG的角度分析了环网潮流不收敛的原因,采用三相模型并应用改进前推回代法对弱环网的配电网进行求解,但该算法随着环网数的增加,收敛性会迅速恶化。文献[10]以回路分析法作为潮流计算的理论基础,并利用配电网各节点电压的相角相差小等特点对回路电压方程进行化简,体现了回路分析法在解决环网问题中的有效性;文献[11]在环网分裂点附近引入符号相反的补偿量,并采用转移矩阵来获得等效补偿功率的修正量,从而使等效补偿功率与节点电压可以同时进行前推回代的迭代过程,体现了前推回代法的迭代过程不仅仅局限在辐射网的潮流计算。
本文基于回路分析法,并结合前推回代法,提出一种含环网配电网改进潮流算法,通过分解支路电流,使得各个分解后的电流分别参与迭代的不同过程,针对环网分裂点电流进行补偿,改变潮流不收敛现象,并且采用与前推回代法相似的实现形式,编程简洁,计算过程简单。
1 前推回代潮流算法
辐射状配电网从任意给定母线到馈线根节点具有唯一路径,前推回代法利用辐射网这一特征,可以沿唯一供电路径修正电压和电流,其收敛性能不受配电网高电阻与电抗比值的影响,具有简单、灵活、方便的优点[12]。
1.1 前推回代潮流算法原理
前推回代潮流算法的基本计算单元如图1所示,该算法主要用于求解系统馈线上各母线的电压和电流。
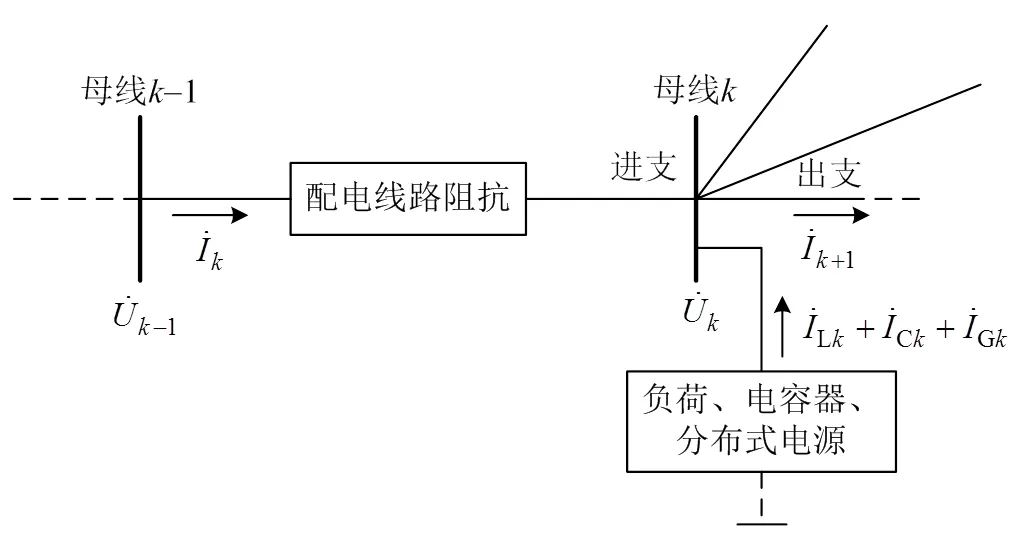
图1 配电网络潮流计算的基本单元
Fig 1 Basic unit of power flow calculation
支路指母线1与母线之间的支路,其阻抗表示为Z,针对支路存在公式:
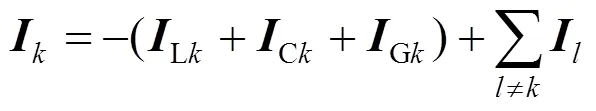
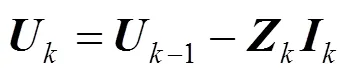
令
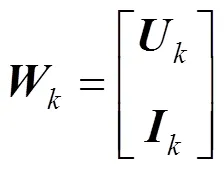
1)前推过程。
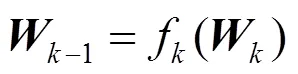
2)回代过程。
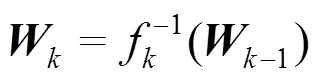
1.2 前推回代收敛性分析
前推回代法是在解决辐射型配电网时,其计算方式符合辐射型配电网的物理特征,具有计算速度快、收敛性好的特点,但是在解决具有环网的配电网时,其收敛性会随着环网支路的增加迅速恶化,甚至不收敛。本文基于文献[13]的研究基础提出收敛指标,从数学的角度找出其不收敛的原因。
在处理含环网的配电网时,前推回代法需要先将连枝支路断开,计算分裂点的等效注入电流brk,其参考方向如图2所示。
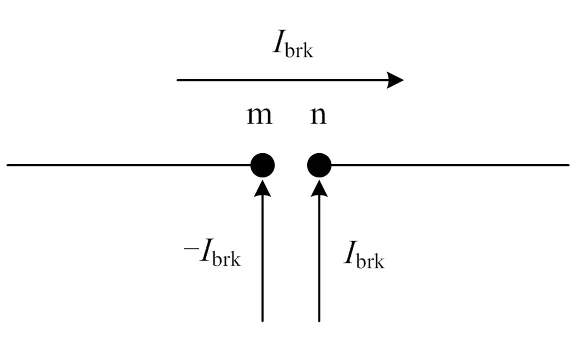
图2 环网等效分裂点
含环网配电网的支路电流计算公式为
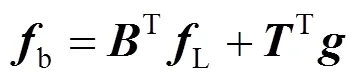
含环网配电网的节点电压计算公式为
式中:b为支路电压;b为支路阻抗矩阵;为支路电压源向量。
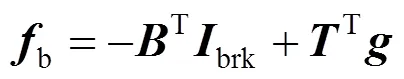
在第次迭代过程中:
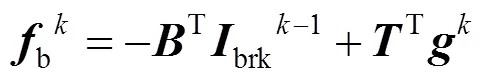
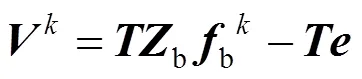
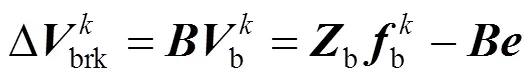
将式(9)代入式(11)可得
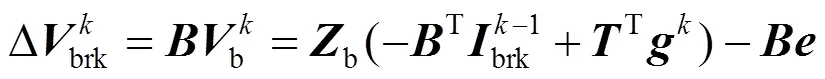
连枝电流差可以表示为分裂点电压差在回路L上形成的电流:
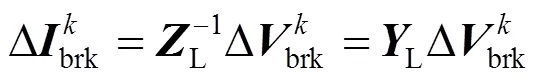
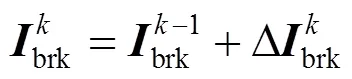
联立式(9)、(12)、(13)、(14)可得
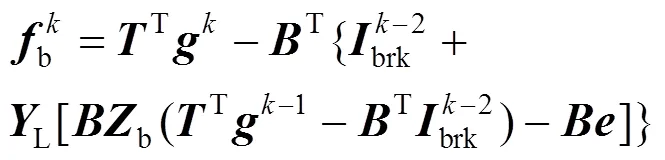
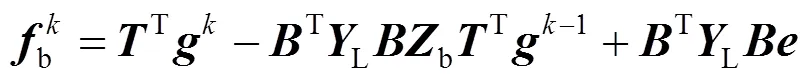
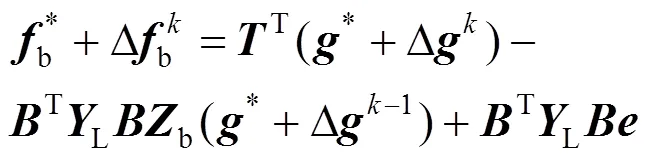
(18)
式(17)减去式(18)可得
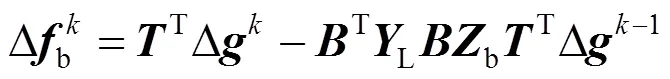
由于公式(19)右边第2项采用了上一次的迭代误差结果,会导致每次迭代过程都会产生一个额外的误差,在环网数量较多时,会由于这个误差而导致迭代无法收敛。
2 回路分析法
2.1 广度优先搜索
本文采用的基于回路分析法的含环网配电网改进潮流算法仍然写成前推回代的形式,针对配电系统需要,应用广度优先搜索形成树枝和连枝。
广度优先搜索算法是连通图的一种遍历策略,主要采用一种辐射性质的搜索方式,从一个节点开始,向与这个节点相关联的其他所有未曾访问的节点进行辐射,然后分别从这些节点出发再依次访问它们的关联节点,直至图中所有节点都被访问过,如图3所示。
在配电系统中,可以使用广度优先搜索,从馈线根节点开始逐层辐射,直至访问完配电系统所有的节点,对配电系统完成分层。由图3可知,从馈线根节点出发,不同层相关联的节点之间的支路为树枝,其余相关联节点之间的支路为连枝。
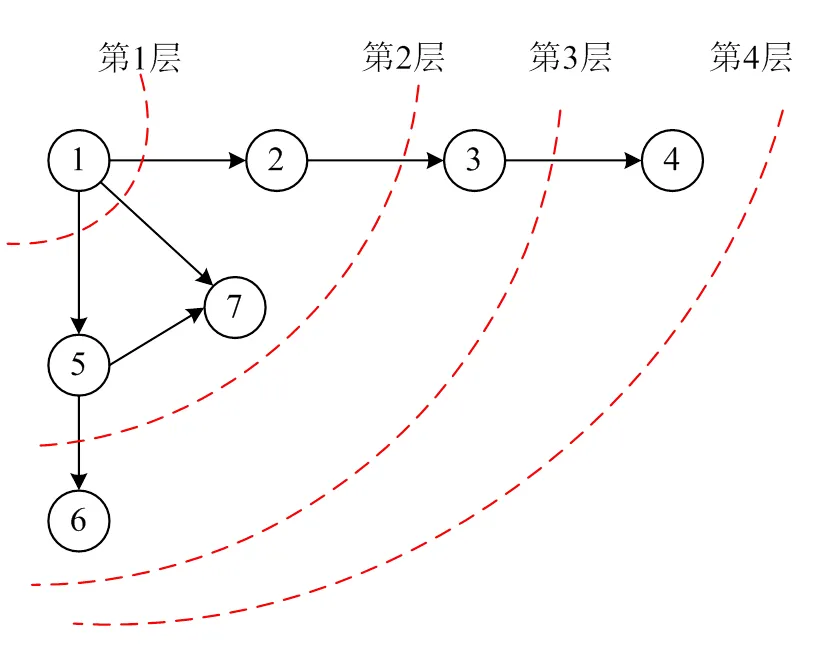
图3 广度优先搜索
2.2 道路矩阵
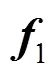
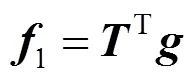
道路矩阵中元素定义为:
将支路安装先树枝后连枝顺序排列,的结构如下:
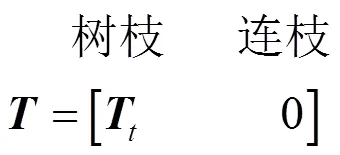
当系统断开所有连枝,只考虑树枝时,由 式(6)可得
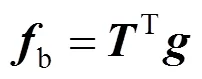
注入电流等于该节点相连各支路电流之和:
(22)
式中为节点支路关联矩阵。
联立式(21)、(22)可得:

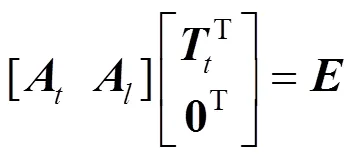
(25)
3 基于回路分析法改进潮流算法
本文采用一种基于回路法的潮流法,该方法可以表示成与前推回代相似的实现形式,但与前推回代法不同的是,其具有强大的处理环网能力。
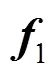
(26)
将这两支路电流分开计算,避免支路电流在每次迭代过程中产生额外的误差。
算法的主要步骤有:
1)首先利用馈线根节点的电压,初始化每条馈线的初始电压。
3)前推计算。
从馈线末端开始,逐层向上计算每个节点的注入电流为
(27)
应用式(26)、(27)计算注入支路电流1和回路支路电流2。
假设节点与上一层节点的联络支路为,则求解节点电压的第次迭代为
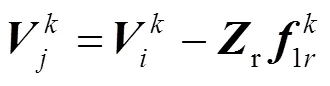
回路的分裂节点对和的虚拟电压差,即为回路第次迭代的回路电压:
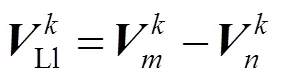
所以可求得回路电流:
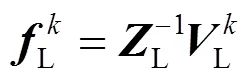
4)回推计算。
从馈线根节点的电压开始向馈线末端逐层更新节点电压。假设节点与上一层节点的联络线,则求解节点电压的第次迭代为
(31)
重复步骤3)、4),直到每个节点在连续2次迭代过程中修正量都小于某一阈值。
基于回路分析法改进潮流算法实现流程如图4所示。
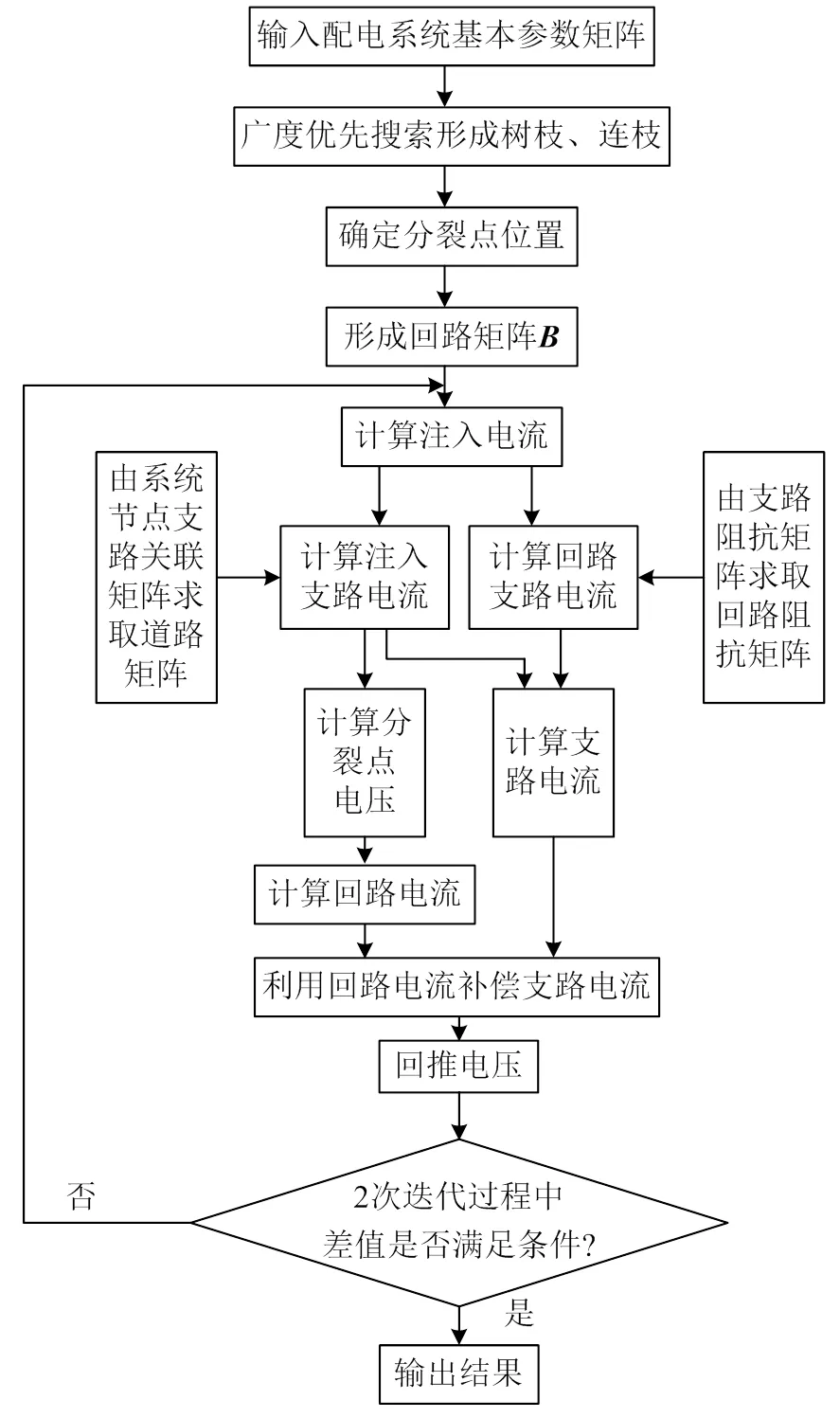
图4 基于回路分析法改进潮流算法流程
4 算例分析
本文以IEEE-33节点配电系统算例进行验证,连接系统5个联络开关,产生5个环路,其拓扑结果以及节点编号如图5所示。
由广度优先搜索遍历形成的树枝和连枝如图6所示,其中,实线为树枝,虚线为连枝,红色箭头表示回路方向。
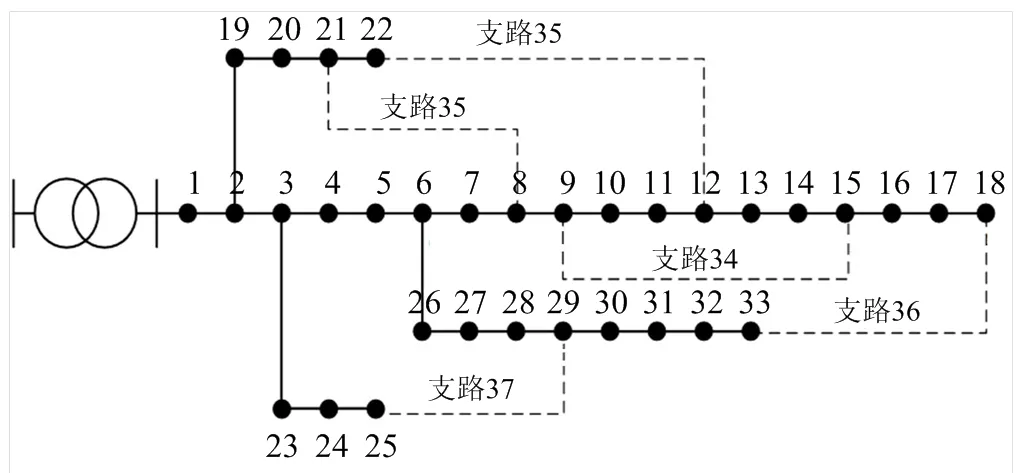
图5 IEEE-33节点配电系统
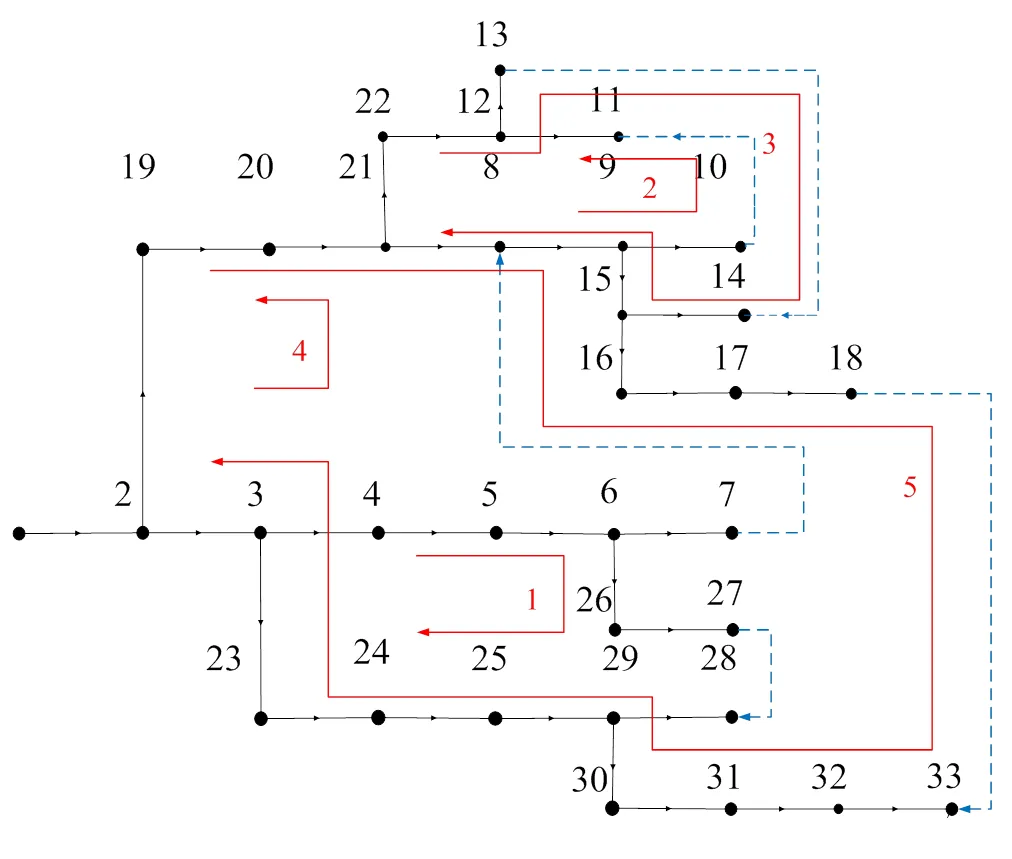
图6 IEEE-33节点配电系统树枝和连枝
采用含环网配电网改进潮流算法,将支路电流分解为注入支路电流1和回路支路电流2,并且针对环网分裂点,利用注入电流计算而来的回路电流进行补偿,使每次迭代结果只与上次注入电流迭代结果相关,避免支路电流在每次迭代过程中产生额外的误差。
算法收敛情况如图7所示。由收敛曲线可以看出该算法有很强的环网处理能力,在系统连接5条环路时仍然可以在8次迭代后收敛。
本文针对IEEE-33节点系统,分别计算了辐射网以及存在5个环路的含环网配电网的节点电压,节点电压分布情况见图8。由图8可见,存在5个环路的含环网配电网的电压分布情况大体与辐射网相同,在联络开关处,含环网配电网节点电压普遍高于辐射网节点电压,符合实际情况。
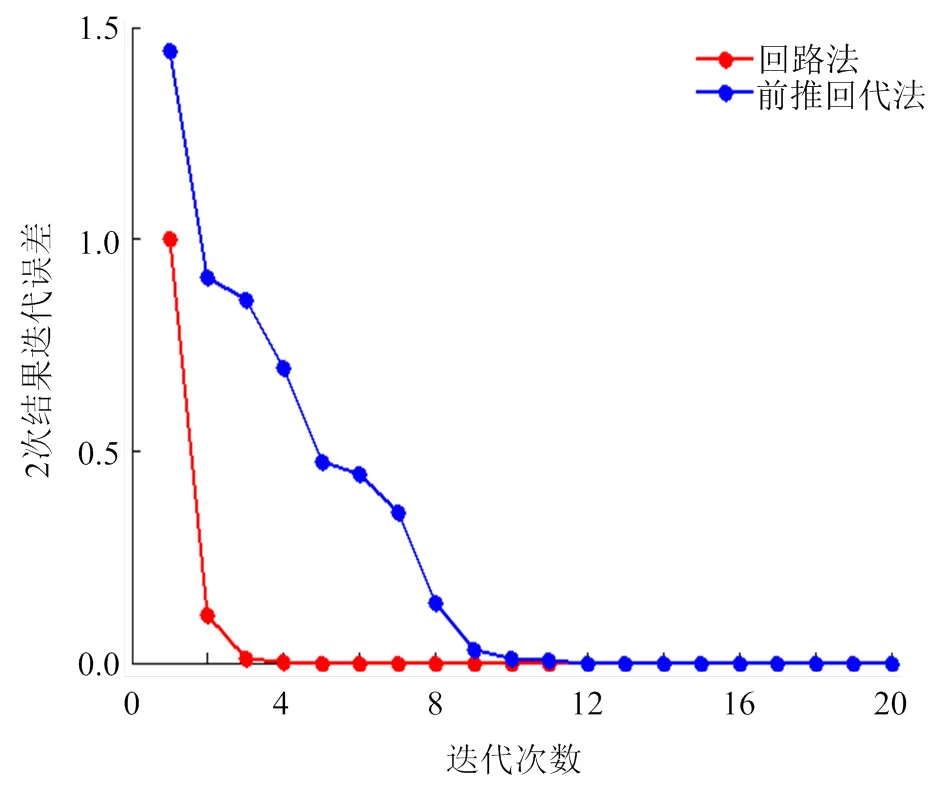
图7 算法收敛曲线
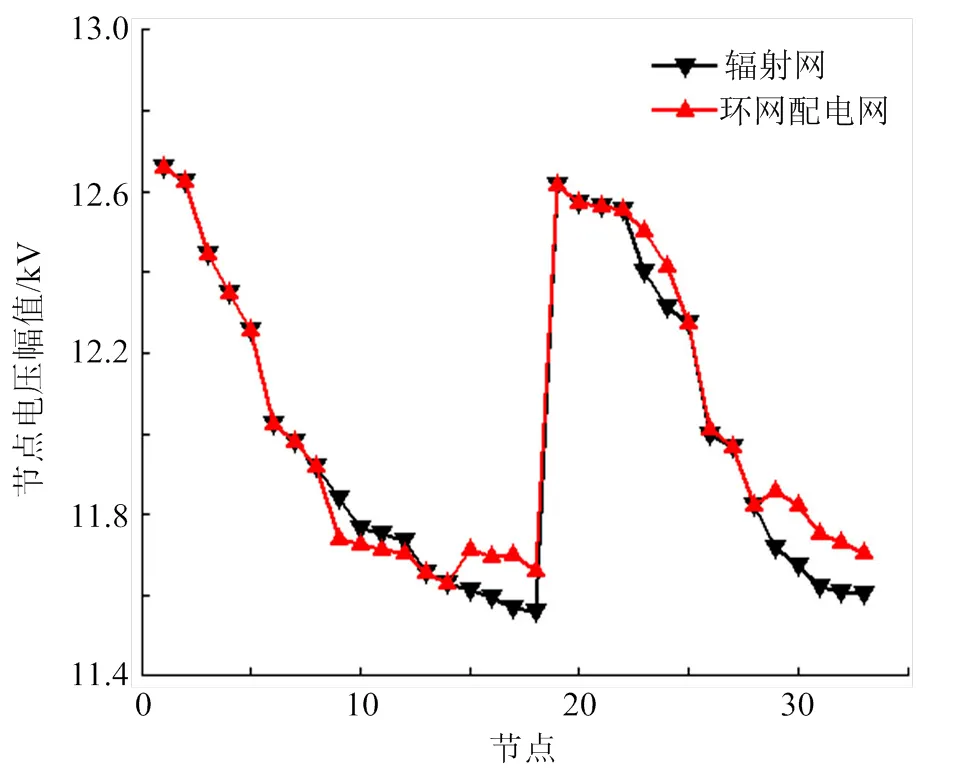
图8 节点电压分布情况
5 结论
研究了含环网配电网的前推回代潮流算法的收敛性,分析了其不收敛的原因,并提出了基于回路分析法的含环网配电网改进潮流算法。该算法将支路电流进行分解,分别参与迭代的不同过程,其具有与前推回代算法相似的实现形式。
理论分析和算例结果均表明:基于回路分析法的含环网配电网改进潮流算法编程简单,收敛速度快,计算复杂度低,在含环网配电网的分析中具有较好的应用前景。
[1]葛乐,陆文涛,袁晓冬,等.背靠背柔性直流互联的有源配电网合环优化运行[J].电力系统自动化,2017,41(6):135-141.
GE L,LU W T,YUAN X D,et al.Back-to-back VSC-HVDC based loop-closed optimal operation for active distribution network[J].Automation of Electric Power Systems,2017,41(6):135-141.
[2]王丽娜.考虑不确定性因素的配电网分布式电源选址定容[J].分布式能源,2018,3(2):23-28.
WANG L N.Locating and sizing of distributed generations in distribution network considering uncertainties[J].Distributed Energy,2018,3(2):23-28.
[3]林青,赵晋泉.输配电网一体化分布式潮流计算方法[J].广东电力,2018,31(6):114-119.
LIN Q,ZHAO J Q.Distributed power flow calculation method for integrated transmission and distribution grid[J].Guangdong Electric Power,2018,31(6):114-119.
[4]张璐,丛鹏伟,许彪,等.基于区域划分的交直流混联配电网潮流计算方法[J].分布式能源,2018,3(6):47-53.
ZHANG L,CONG P W,XU B,et al.A hybrid AC/DC distribution network power flow calculation method based on area partition[J]. Distributed Energy,2018,3(6):47-53.
[5]罗煜,吴杰康,简俊威,等.基于机会约束规划的多类型分布式电源容量与布点优化方法[J].广东电力,2018,31(4):34-42.
LUO Y,WU J K,JIAN J W,et al.Optimization method for multi-type DG capacity and stationing based on chance constraint programming[J].Guangdong Electric Power,2018,31(4):34-42.
[6]王守相,黄丽娟,王成山,等.分布式发电系统的不平衡三相潮流计算[J].电力自动化设备,2007,27(8):11-15.
WANG S X,HUANG L J,WANG C S,et al.Unbalanced three-phase power flow calculation for distribution power generation system[J].Electric Power Automation Equipment,2007,27(8):11-15.
[7]梁梦可,滕欢,李雪松,等.前推回代法在故障配电网中的收敛性分析及改进算法[J].电测与仪表,2018,55(9):9-13,17.
LIANG M K,TENG H,LI X S,et al.Convergence analysis of forward/backward sweep substitution for power distribution network and improved algorithm[J].Electrical Measurement & Instrumentation,2018,55(9):9-13,17.
[8]顾晨,乐秀璠,张晓明.基于改进前推回代法的弱环配电网三相潮流计算[J].电力系统保护与控制,2010,38(19):160-164.
GU C,LE X F,ZHANG X M.Three-phase power flow method for weakly meshed distribution systems based on modified back/forward sweep method[J].Power System Protection and Control,2010,38(19):160-164.
[9]李红伟,孙宏斌,张安安,等.基于正序分量的含PV节点的三相配网潮流算法[J].中国电机工程学报,2012,32(1):115-121.
LI H W,SUN H B,ZHANG A A,et al.Positive-sequence Component Based Three-phase Unbalanced Power Flow Solution for Distribution System With PV Nodes[J].Proceedings of the CSEE,2012,32(1):115-121.
[10]牛焕娜,井天军,李汉成,等.基于回路分析的含分布式电源配电网简化潮流计算[J].电网技术,2013,37(4):1033-1038.
NIU H N,JIANG T J,LI H C,et al.Simplified power flow calculation for distribution network with distribution generation based on loop analysis[J].Power System Technology,2013,37(4):1033-1038.
[11]闫宏亮.弱环网潮流简化分析及其在配电网优化控制中的应用[D].西安:西安石油大学,2004.
YAN H L.Simplified analysis of weak loop power flow and its application in optimal control of distribution network[D].Xi’an:Xi'an Shiyou University,2014.
[12]王守相,王成山.现代配电系统分析[M].北京:高等教育出版社,2014:124-125.
WANG S X,WANG C S. Analysis of modern distribution system[M].Beijing:Higher Education Press,2014:124-125.
[13]WU W C,ZHANG B M.A three-phase power flow algorithm for distribution system power flow based on loop-analysis method[J].International Journal of Electrical Power & Energy Systems,2008,30(1):8-15.
Improved Power Flow Algorithm for Distributed Ring Network Based on Loop Analysis
GU Si1, SUN Xiao1, MA Chang2, CHEN Jing2
(1. School of Electric Power Engineering, Nanjing Institute of Technology, Nanjing 211167, Jiangsu Province, China;2. Xinjiang Fukang Pumped Storage Co., Ltd., Fukang 830011, Xinjiang Uygur Autonomous Region, China)
In order to improve the ability of clean energy consumption and the reliability of power supply, distribution network operation is attracting more and more attention. In view of the non-convergence of the traditional forward and backward substitution method, an improved power flow algorithm for distribution network with ring network was proposed by combining the loop analysis method with the forward and backward generation power flow algorithm. The branch current was decomposed to compensate the split-point current, and the non-convergence phenomenon was changed. The validity and accuracy of the algorithm were verified by data simulation with Matlab.
distribution network; distributed generation; loop operation; loop analysis; forward and backward substitution method
10.12096/j.2096-4528.pgt.18232
TK 01; TM 727
2020-02-06。
(责任编辑 辛培裕)

