爬楼轮椅的改进设计与相关特性分析

朱 阳，邱卫明

（台州广播电视大学高职学院，浙江 台州318000）

0 引言

当前，中国社会的老龄化趋势越来越显著，老年人与腿脚不便者所占比重不断上升[1]。对于多数老年人与腿脚不便者来说，轮椅是一种非常重要的代步工具。但普通轮椅仅适于水平或倾斜度不大的路面行驶，如遇台阶，基本需要借助外人的搬动。主要原因是普通轮椅缺少与翻越障碍物等相关的爬楼机构。而目前大部分爬楼轮椅价格昂贵，且体积较大，常见的公寓式楼道过于狭小，使用不便[2]。因此，生产一种体积较小巧、价格适中、行走平稳的爬楼轮椅将非常适合中国的市场。

1 方案的确定

1.1 总体方案的分析

爬楼轮椅根据其工作原理，除了一些采用多种辅助机构外，一般常采用腿足式、履带式，行星轮式等[3]，因此，首先需要在对各种机构的优缺点进行分析的基础上确定总体方案。

1.1.1 腿足式

腿足式是市场初期出现的爬楼轮椅所采用的铰链杆件装置，外形上有点像机器人。爬楼的时候，通过机械臂的交替运动先是升高轮椅，然后向前水平运动，爬楼过程就是这两个运动的重复，基本上是对人类爬楼过程的模仿[4]。

从机构角度分析，腿足式爬楼轮椅的灵活性强，能很好地适应不同地形，行走于大多数楼道、路面没有问题。缺点是腿足式爬楼轮椅的铰链杆件装置机构复杂、效率低，不能实现较高速度的稳定行走。

1.1.2 履带式

履带式爬楼轮椅在技术也是相对成熟的，原理基本类似于履带式装甲车。在楼梯上运动时，它的重心始终会平行于楼梯台阶边缘连线，从而减小整个装置的重心在运动过程中的波动性，达到运动平稳的目的[5]。由于履带跟路面的接触面积大，压强小，使得该机构的越障、爬坡等性能良好，能通过各种复杂的地形。

履带式爬楼轮椅的缺点较多：一是质量、体积较大，传动效率低，虽然越障、爬坡等性能好，在楼梯上运动优势明显，但是在平地行驶的时候不容易实现速度要求；二是爬楼过程中，该机构向上向前的动力主要来源于履带跟台阶边缘的摩擦，一定程度上会对台阶形成破坏；三是履带机构转弯半径大，在较窄的楼道上转弯，会加大操作难度。四是履带机构在楼道转弯时，靠的是左右履带的速度差甚至是左右履带的相反运动，就必然会使履带与地面发生滑动摩擦。为了爬楼的稳定性，履带与地面的摩擦系数一般很大。所以这种滑动摩擦加大了履带与楼道台阶面的摩擦磨损。

在综合考虑爬楼轮椅的实用性、经济型等情况，也考虑降低设计难度的要求，可以在爬楼轮椅上采用一种新型的行星轮机构，即装在轮椅底盘的行星轮机构，既用来实现爬楼的功，也用来实行平地行走功能。

1.2 爬楼方案的确定

首先可以设计一根包括外圈轴与中心轴在内的同心轴，轮椅在水平路面行驶时，电机将运动传给中心齿轮10，中心齿轮通过花键将运动传给外圈轴，从而完成驱动过程。当轮椅处于爬楼状态时，电机直接将运动传给中心轴，通过行星轮架3的翻转完成驱动过程。为了顾及乘坐者的感受及轮椅在爬楼时候的稳定性，可以让轮椅在水平行驶与爬楼时的运动方向不同，即倒着爬楼，类似于汽车变速箱中的通用技术，无须增加电机，只要通过齿轮等构件的滑移即可实现双向驱动。齿轮和轮架之间的关系如图1所示。

图1 轮架和齿轮图

1.3 行星轮的个数的确定

行星轮太少会导致轮椅在爬楼过程中重心波动较大，降低稳定性与舒适性[6]。行星轮太多会减小各行星轮之间的中心距，使整个轮系的最大越障高度降低。同时增加行星轮使得轮椅体积增大，不仅降低了轮椅在楼道上的灵活性，而且导致系统控制的复杂化，降低了水平路面行驶时的效率[7]。综合稳定性、灵活性与效率的考虑，可以在轮椅中使用三个行星轮（如图1左图）。

2 行星轮爬楼轮椅的运动特性分析

2.1 前提与假设

在分析行星轮爬楼轮椅运动特性之前，根据实际情况，对运动系统作了一定的简化：

（1）地面（含楼道台阶等）、轮架（图1中的3）、轮椅骨架、行星轮等视为理想的刚体；

（2）由于外轮胎厚度不大，其对轮椅运动过程的影响忽略不计；

（3）只要设计合理，爬楼轮椅的重心与其运动中心重合；

（4）整组行星轮系统可以当作一个轮子，也就是后轮看作由两个大轮组成；

（5）与地面接触的轮子不考虑滑动现象，只考虑作纯滚动。

2.2 轮椅的平动模型简化分析

一般家用的爬楼轮椅，其平面运动状况都可以简化为水平行驶模式和爬楼模式两种，因此对这两种模式进行简化并分析。

2.2.1 水平行驶模式

图2所示为爬楼轮椅在水平路面行驶的简化模型，前面的两个小轮起转向作用，是转向轮，后面的两个大轮由行星轮系简化而来，与电机相连，作为驱动轮。设坐标系为XOY并与车体固定在一起。

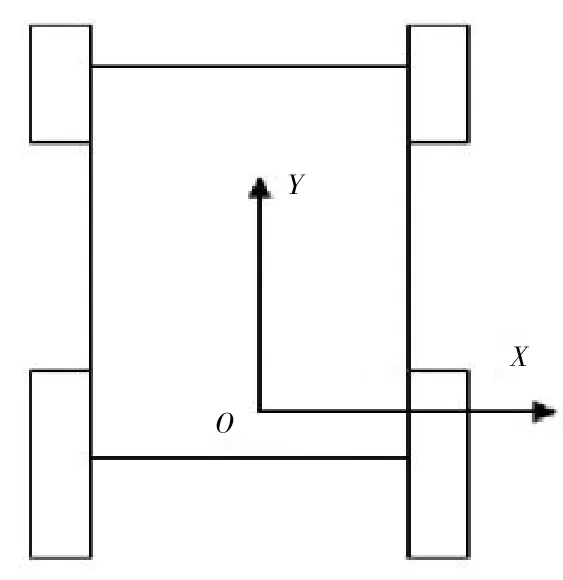
图2 轮椅在水平路面行驶模型

当爬楼轮椅在水平路面进行直线行驶时，轮椅前面的小轮（转向轮）与后面的大轮（驱动轮）在线速度的大小和方向上完全相同，前后轮子的线速度跟轮椅的移动速度也是大小相同、方向一致，因此都设为V0。

当爬楼轮椅在水平路面转向行驶时，如图3所示。由于一般转向过程的侧偏角较小，其对轮椅的影响可以忽略不计，因此轮椅前面的小轮（转向轮）轴线的延长线与后轮（驱动轮）轴线的延长线必交于一点。设爬楼轮椅前后轮轮轴之间的距离为D，转向过程中转向轮的转角为α，根据图3几何关系可得：

图3 轮椅转向示意图

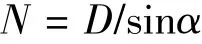
即轮椅的最小转弯半径等于轮椅的前后轮轴距D，此时轮椅转向轮达到极限转角值90°。

2.2.2 爬楼模式

当轮椅需要爬楼时，可以切换到倒着爬楼的模式，由电机驱动中心轴，中心轴再把运动传到轮架（图1中的3），轮架翻转，完成爬楼过程。根据假设5，左右对称分布的车轮与楼梯之间没有滑动，只作纯滚动，如果用VL、VR分别表示左、右两侧车轮的线速度，则VL=VR。由于是倒着爬楼，在爬楼瞬间，轮椅前面的小轮（转向轮）处于悬空状态，只有后轮（驱动轮）着地，如图4所示。

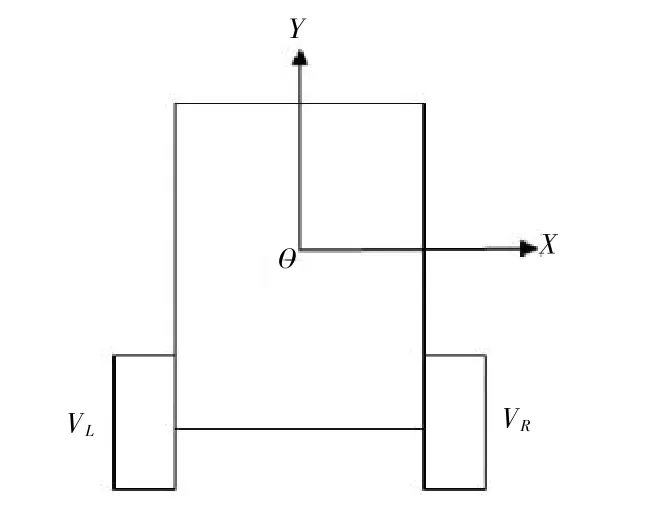
图4 轮椅爬楼瞬间模型

3 越障力学分析

对爬楼轮椅进行越障力学分析，目的是了解轮椅的越障能力，为进一步的轮架半径设计提供依据。越障力学分析可以分为两种情况，一是轮组直接“爬”过台阶，二是轮组通过翻转从而跨越台阶。

3.1 爬过台阶

图5所示为轮椅的驱动轮“爬”台阶时的过程分析。设轮 1、2 所受到的驱动力分别为f1、f2，t1、t2、t3分别为为轮1、2、3所受到的地面的接触反力，M为轮架中心至轮3中心的距离，M1为轮架中心至底盘重心处的距离，M2为轮3至底盘重心处的距离，N为轮架中心至轮1中心的距离，h为台阶高度，r为轮1的半径，α为轮1与台阶接触处的相关角度，附着系数（可以认为是轮胎和路面之间的静摩擦系数）为b。根据受力分析，只有当轮1即将离开地面的瞬间，所需要的驱动力达到最大，由于滚动阻力太小而忽略不计，列出如下平衡方程[8]：

图5 “爬”台阶过程分析

由于工作中电机对轮1、2的驱动力矩相同，轮胎和路面之间的附着系数为b，则

在路面较硬时，可以假设路面对轮1、2在竖直方向上的反力相等，即

第一种情况，假设t1＜t2，则

将6式代入1式中解得b（1+cosα）=sinα

第二种情况，假设t1＞t2，则

联立 1 式、5 式、7 式，解得b（1+cosα）=sinα

可见，无论t1、t2之间的大小关系是怎么样，结果是一样的，即

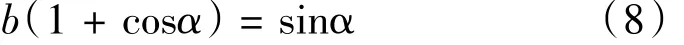
由几何关系可以得到

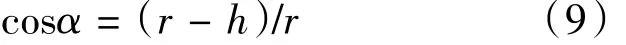
由（8）式解出

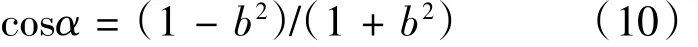
将（10）式代入（9）式解得

2b2/（1+b2）即为轮组可以不通过翻转而直接“爬”过去的最大台阶高度。

3.2 翻转跨越台阶

根据一般居民楼道情况，可以认为台阶的转角处为90°，轮组通过翻转跨越台阶的过程如图6所示。

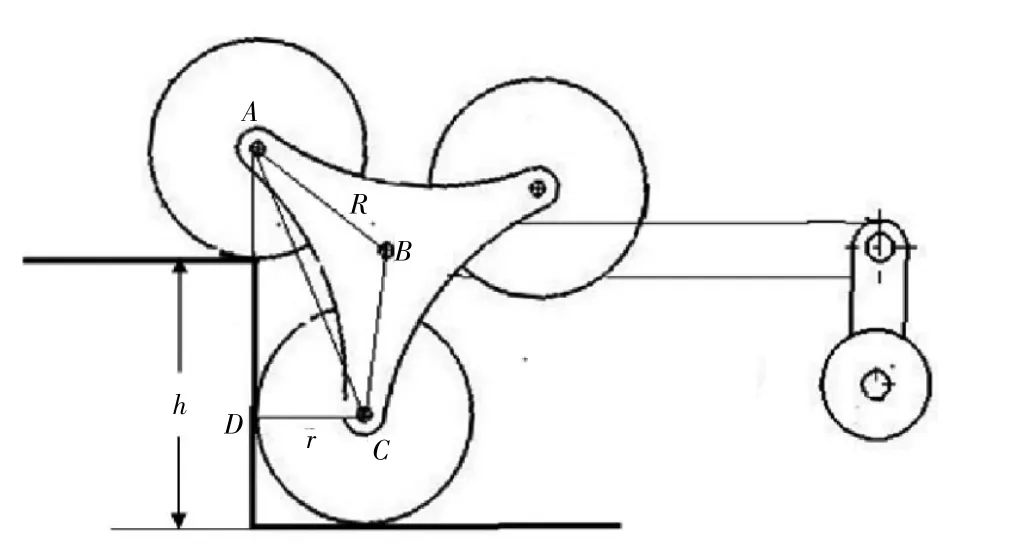
图6 翻转过台阶过程分析

图中台阶高度AD设为h，翻转轮架半径AB设为R，轮的半径CD设为r，由几何关系得到：

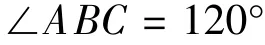
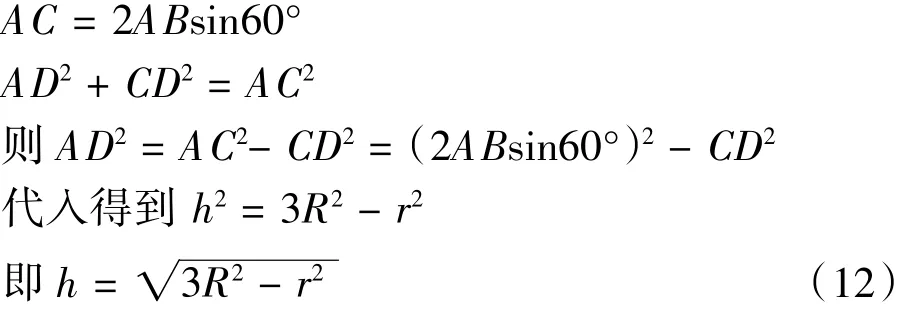
由h=2b2（/1+b2）和可以知道行星轮越障极限，可以为后续总体设计中的轮架半径设计提供理论依据。

4 结论

通过对行星轮爬楼轮椅在水平路面运动和爬楼过程这两种模式的运动特性分析，得到了轮椅在水平路面进行直线和弯道运动以及爬楼过程中的速度、位置等数据。再通过对轮椅越障时轮组采用“爬过”和“翻转过”这两种模式进行了力学分析，得到了轮组的越障极限等数据。这些数据均可作为后续总体设计的理论依据。