连续式跨声速风洞压力损失计算研究

李庆利,孟凡民,李兴龙,张 刃,崔晓春

(中国航空工业空气动力研究院 高速高雷诺数气动力航空科技重点实验室,沈阳 110034)

0 引 言

风洞试验设备是航空飞行器研发的重要支撑。无论是飞行器设计还是风洞设计，跨声速都是气动力问题最为复杂的领域之一[1]。各航空航天大国都不遗余力地建造了各种先进的跨声速风洞设备，大型连续式跨声速风洞已经成为世界发达国家的重要战略资源。

国内连续式风洞大多为低速风洞,因此国内关于连续式风洞损失估算方法基本以低速为主。国际上公开文献有高速连续式风洞估算方法，但最复杂的试验段部分基本参考引导风洞试验数据修正而来。为此，本文结合CFD手段，分析获取了试验段损失特性。

在连续式风洞各个系统设计之初，需要对整个风洞气动性能进行估算，以达到以下目的：

(1) 计算得到压缩机、冷却器等设备出、入口的流量、压力、温度等条件，以开展压缩机、冷却器等系统设计工作；

(2) 为洞体载荷和强度计算提供输入条件；

(3) 计算研究马赫数(Ma)、压力和温度间的耦合影响关系，为压力和温度控制系统提供输入条件，同时基于耦合关系给出相互间影响量值，以供关键控制设备选型。

风洞部段气动性能计算的前提便是获取风洞沿程的压力损失，作为部段参数计算的输入条件，因此需针对风洞压力损失估算方法进行研究和验证。

1 0.6 m连续式跨声速风洞概述

0.6 m连续式跨声速风洞(简称FL-61风洞)主要由稳定段、收缩段、半柔壁喷管、试验段、第二喉道、亚声速扩散段、第一拐角、第二拐角、压缩机、低速扩散段、冷却器、第三拐角、气体补充段和第四拐角等部段组成。洞体总长约26.7 m，宽约8.45 m，风洞整体布局见图1。

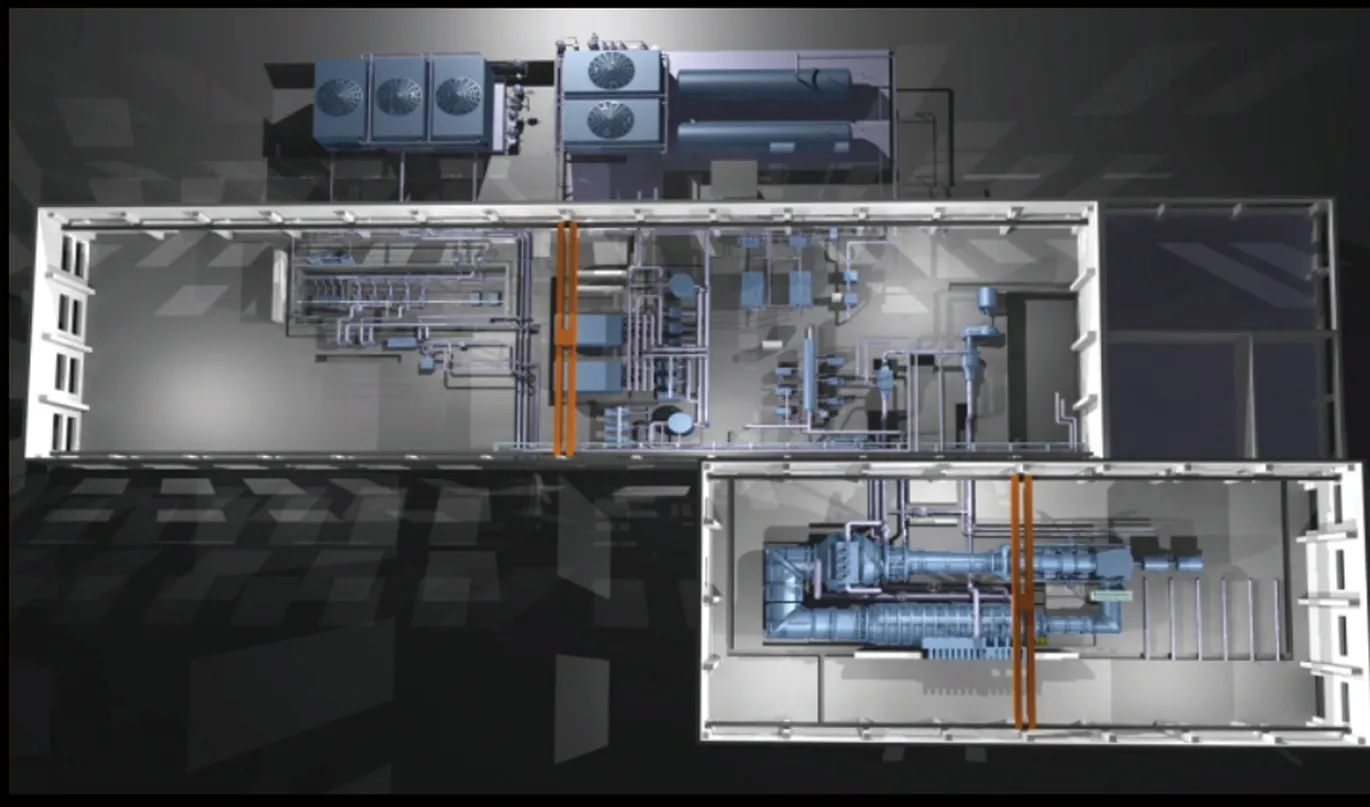
图1 FL-61风洞布局图Fig.1 The FL-61 wind tunnel layout

为实现较大的低超声速(Ma=1.2～1.5)试验范围并兼顾不同尺寸试验段要求，采用半柔壁喷管技术。对亚声速二喉道与超声速二喉道进行综合设计，第二喉道段左右壁板采用可调超扩段壁板(左右壁板可调，上下壁板固定)，第二喉道中间截面布置支架尾延板与马赫数微调机构，以提高马赫数控制效率及试验段动态流场品质。另外风洞还配备许多辅助系统以保证风洞的正常运行。

连续式风洞为封闭的气动回路，气体在沿着管道流动过程中，由于洞壁摩擦及流动分离等造成沿程压力的损失，并通过压缩机对整个流道的压力损失进行弥补。同时需用风洞内部换热器置换出压缩机带入流道内的能量，避免温度持续上升，以维持整个风洞在设定工况下稳定地运行。

2 计算方法

2.1 理论估算

首先将风洞顺气流方向分为试验段、第二喉道段、再入段、方变圆段、第一扩散段、第一拐角段、一二拐角间等直段、第二拐角段、压缩机段、第二扩散段、大角度扩散段、风洞冷却器、大角度收缩段、第三拐角段、三四拐角间等直段、第四拐角段、稳定段、收缩段、喷管段等19个部段。然后，结合CFD计算分析和流体阻力手册中经验数据对各部段压力损失系数进行估算。

因高速风洞透气壁流动的复杂性，且在跨超声速下还会出现激波，因此在本文开展的工作中，对高速风洞损失估算的重点部段(试验段)进行了详细分析，并通过CFD计算和损失估算经验公式相结合的方式，给出了透气壁试验段损失的估算方法。

高速风洞的风洞回路损失与低速风洞类似，虽然也是通过逐段计算各部段的压力损失而得到，但不同的是，高速风洞的收缩段、试验段和扩散段等流动是可压缩的，其密度不是常数，需进行压缩性修正[2]。对于恒定截面积部段、扩散段和收缩段等风洞中常见部段，损失多数采用基于带壁面摩擦力的一维可压缩流对Darcy-Weisbach方程积分而来，多数方程如Voronin压缩性修正方程等在亚声速范围有很好的适用性[3]；此外，Wolf给出的一个压缩性修正方程[2,4]，在低超声速范围能得到很好的修正效果，其修正经验公式给出了不可压缩流的压力损失系数Kic：

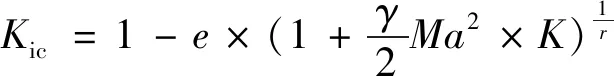
(1)

通过以上估算手段可获取风洞各部段压力损失系数，最终通过式(2)迭代计算，获得各部段的压力损失[6]：

(2)

式中：εi为风洞第i段压力损失；ξi为第i段损失系数；q(λi)为第i段入口速度系数函数；λi为第i段入口速度系数。

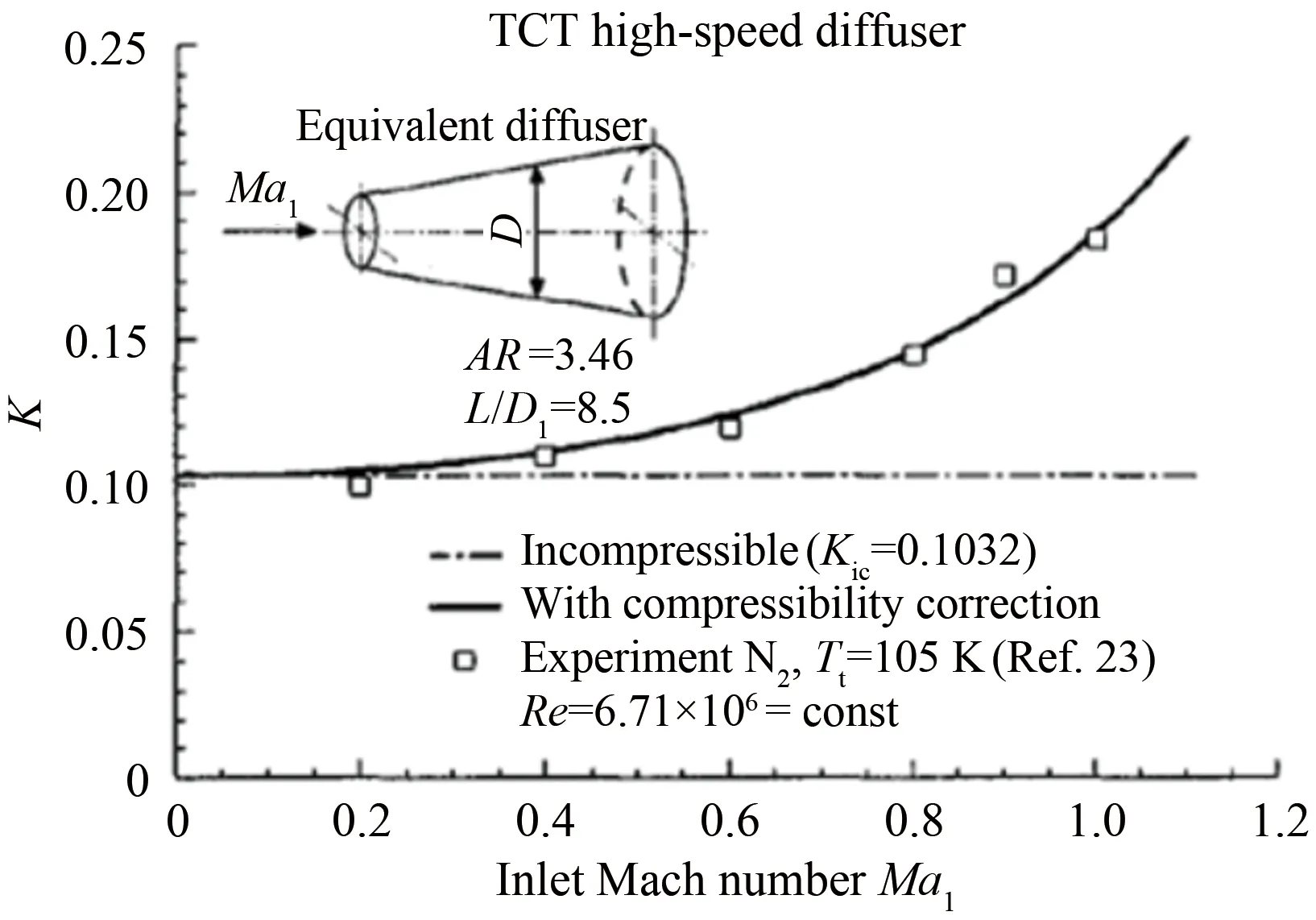
图2 TCT风洞高速扩散段压缩性修正对损失的影响[5]Fig.2 Effect of high-speed diffuser compression modification on loss of TCT wind tunnel[5]

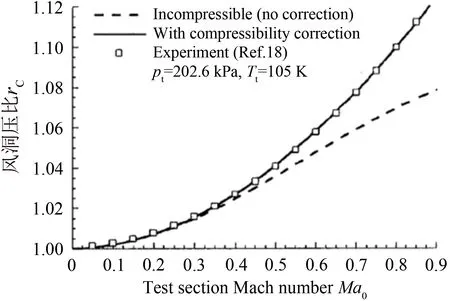
图3 TCT风洞压比估算值和测量值的对比[5]Fig.3 Comparison of estimated and measured pressure loss in TCT wind tunnel[5]

2.2 CFD计算

为研究槽壁试验段流场特性,对槽壁试验段的单条槽缝进行数值模拟。计算模型如图4所示，在开槽壁试验段中取出一条槽缝、其下方的驻室空间和其上方的1/2试验段空间，Flap片开度和试验段壁板角均为0°。

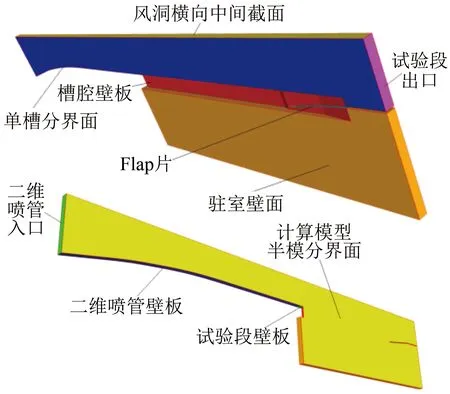
图4 槽壁试验段示意图Fig.4 The slotted test section

为排除网格不对称性并减少网格量，采用半模计算。用ICEM-CFD网格软件构建模型的结构网格，网格节点数为6 102 717，边界层网格数为33，物面第一层网格高度为0.01 mm，驻室壁面为无边界层网格。槽壁试验段网格见图5。采用Fluent求解器进行计算，湍流模型选用k-wSST模型，具体边界条件如表1所示。

图5 槽壁试验段网格Fig.5 Mesh of the slotted test section

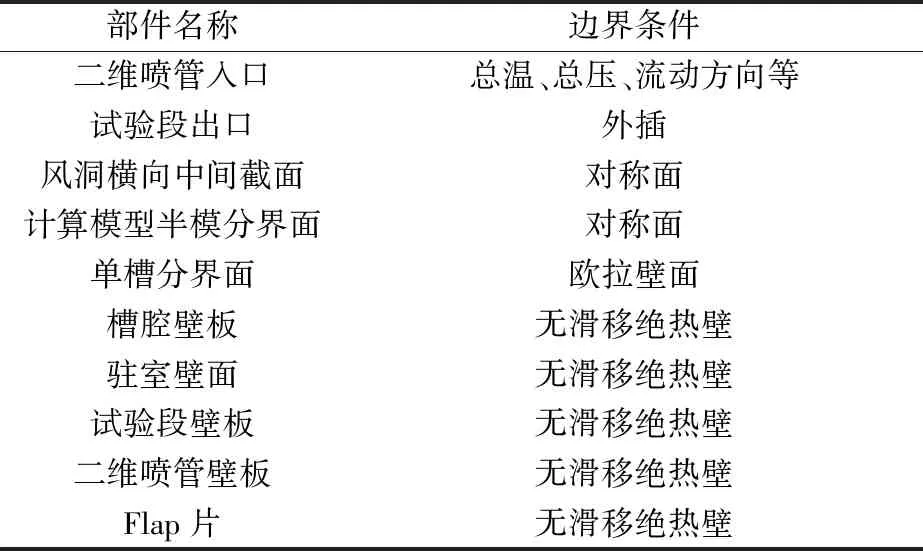
表1 边界条件一览表Table 1 List of boundary conditions

3 风洞部段压力损失估算

3.1 跨声速试验段损失计算

跨声速风洞试验段为整个风洞管道中截面最小的部位，也是达到试验工况运行参数的部段，因此将试验段作为整个损失计算的起点，以便更直接地得到所要求试验工况下的风洞性能数据。高速风洞为实现跨声速速域范围，需采用透气壁形式，包含透气壁排气损失、再入扩张损失、跨声速激波损失、模型支撑及尾延板损失等。图6给出了试验段主要损失分布示意图。

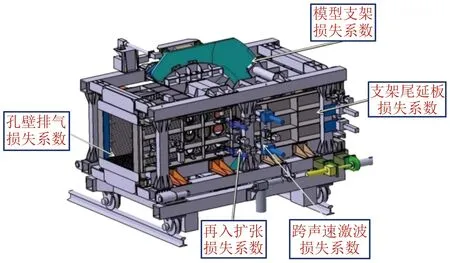
图6 试验段主要压力损失Fig.6 Main pressure loss in the test section

根据透气壁试验段所具有的明显的气动特点，将试验段出入口的压比ε1分解为4个部分：

ε1=εa·εb·εc·εd

(3)

式中：εa为透气壁板产生的压比；εb为模型产生的压比；εc为试验段主流引射及激波等带来的压比；εd为模型支架产生的压比。

本文仅对试验段马赫数Ma=1.00工况作全面的介绍，其他工况基于相同方法通过编程批量计算获得。

3.1.1 透气壁板产生的压比εa

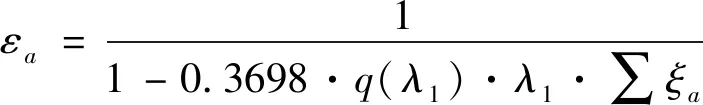
(4)

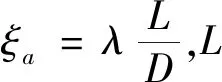
在Ma=1.00工况下，试验段速度系数λ1和速度系数q(λ1)函数均为1，因此：

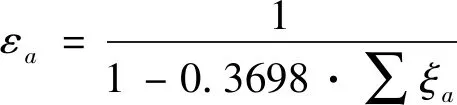
(5)

对于普通钢制管道，摩阻系数经验公式为：

(6)

在总温T0=310 K，总压p0=0.1 MPa时，马赫数Ma=1.00下的雷诺数Re=8.365×106，由此可得λ′=0.0085。

基于Voronin压缩性修正方程，计入压缩性影响[2]：

(7)

根据高速风洞运转经验，透气壁在Flap片完全关闭(开度为0°)时，由于边界层增长的影响，在出口处将形成喉道，整个试验区Ma在0.90左右(CFD模拟结果见图7，其中pexit为试验段出口静压，p0为试验段总压)。而跨声速的主流引射则是恰好通过抽吸1%的主流气体以避免此堵塞影响，使试验段达到Ma=1.00的状态。相关文献也给出了不同Ma下驻室排气量的试验结果，验证了这一结果(详见图8)，图中给出了不同喷管Ma下，要达到试验马赫数需要通过透气壁的流量[7]。因此需计入壁板开孔的影响，沿程在侧壁有流体流入或流出，沿程阻力系数也一直在改变，参考同类型管道流体阻力的经验公式[8]：

(8)

图7 Flap片关闭状态下计算结果Fig.7 The calculated results in flap off state

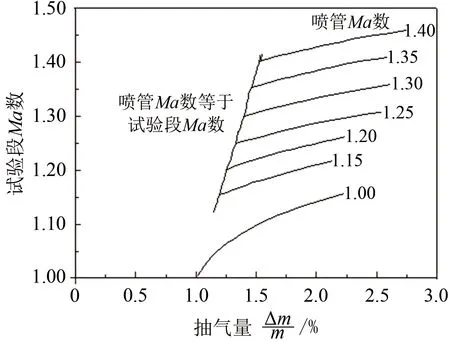
图8 不同喷管和试验段Ma数下抽气量[7]Fig.8 The suction mass at different nozzles and different Mach numbers[7]

3.1.2 模型产生的压比εb

vmod=1-(0.04127/20)αmodMa2

(9)

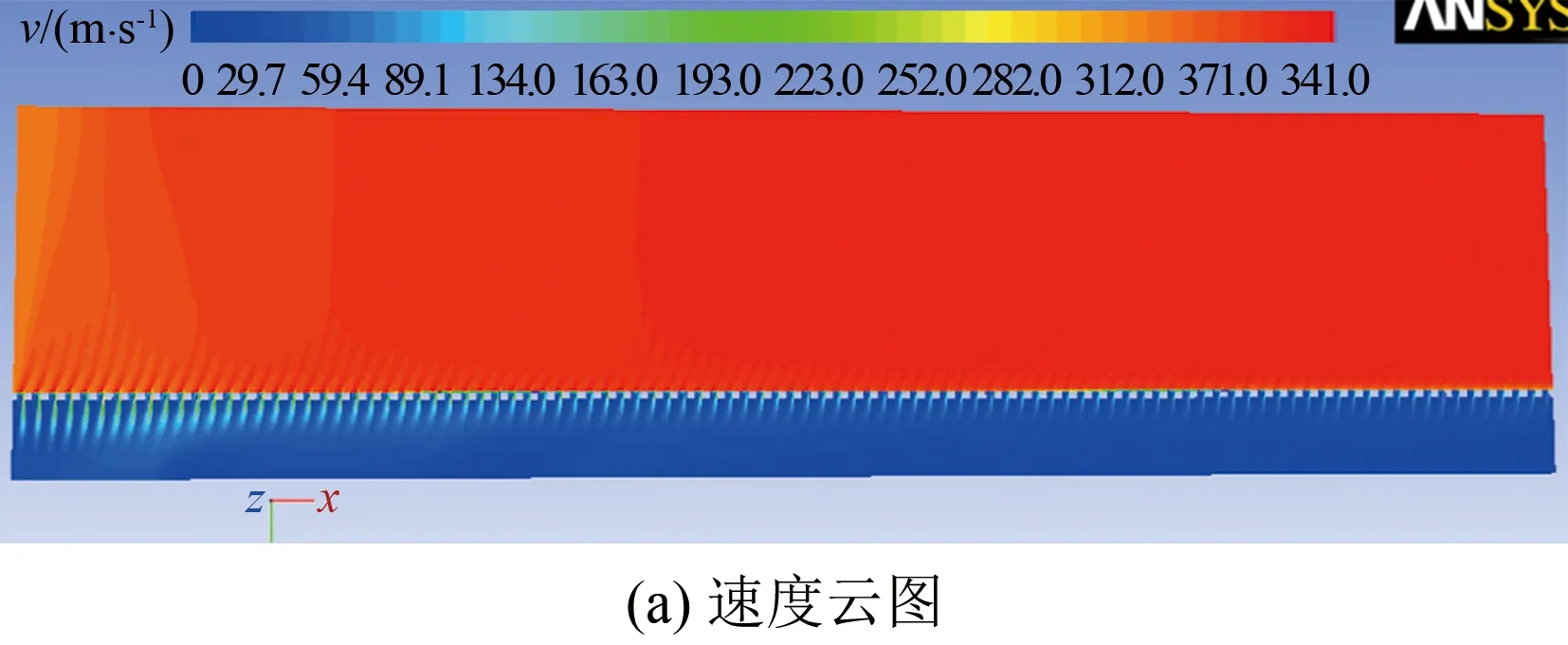
图9 孔壁试验段简化模型(二维)CFD计算结果Fig.9 Calculation results of the simplified model (2D) for perforated-wall test section

3.1.3 试验段主流引射及激波等带来的压比εc

高速风洞不同跨声速马赫数状态下，部段内激波形式有很大的不同，因此需针对各马赫数下试验段内激波进行单独的分析。

(1) 试验段马赫数Ma=1.00工况

由于高速阻塞影响等因素，需自试验段透气壁流出约1%的主流流量来抵消附面层位移厚度带来的阻塞影响。试验段再入区的面积增加，Ma会进一步增加，使试验段再入区压力低于驻室压力，对驻室内的气体起到抽吸作用，而后与被引射气体混合，达到主流引射的目的。该过程中被引射气流仅为主流的1%，而扩开面积比达到1.35，因此可近似为主流流过盲腔时形成扩张损失，根据鲍尔德-卡尔诺公式：

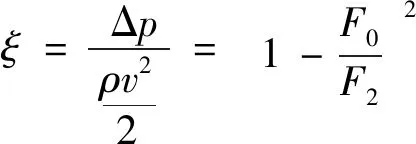
(10)

其中，Δp为损失压力值；F0为试验段面积；F2为试验段再入区总面积。由式(10)得出该部位扩张冲击损失系数为0.0672。

另外，在低超声速(Ma=1.20～1.50)范围，支架段扩张将使主流进一步膨胀，主流静压得以进一步降低，对驻室气体起到抽吸作用；随着驻室气体再次进入主流道，主流中形成激波系，使得主流被压缩，马赫数开始减小。对于FL-61风洞试验段出口处的膨胀状态来说，根据0.2 m量级试验段试验结果(见图10)，经第一道膨胀波膨胀后，激波系前的马赫数为1.34。

在支架影响下，将形成较强波系，同时在主流引射试验工况下，该膨胀波后即形成主流引射再入。相关文献也表明，在低超声速范围，波系损失往往通过简化为波前马赫数对应的正激波损失[2]，因此取Ma=1.34对应的激波损失。

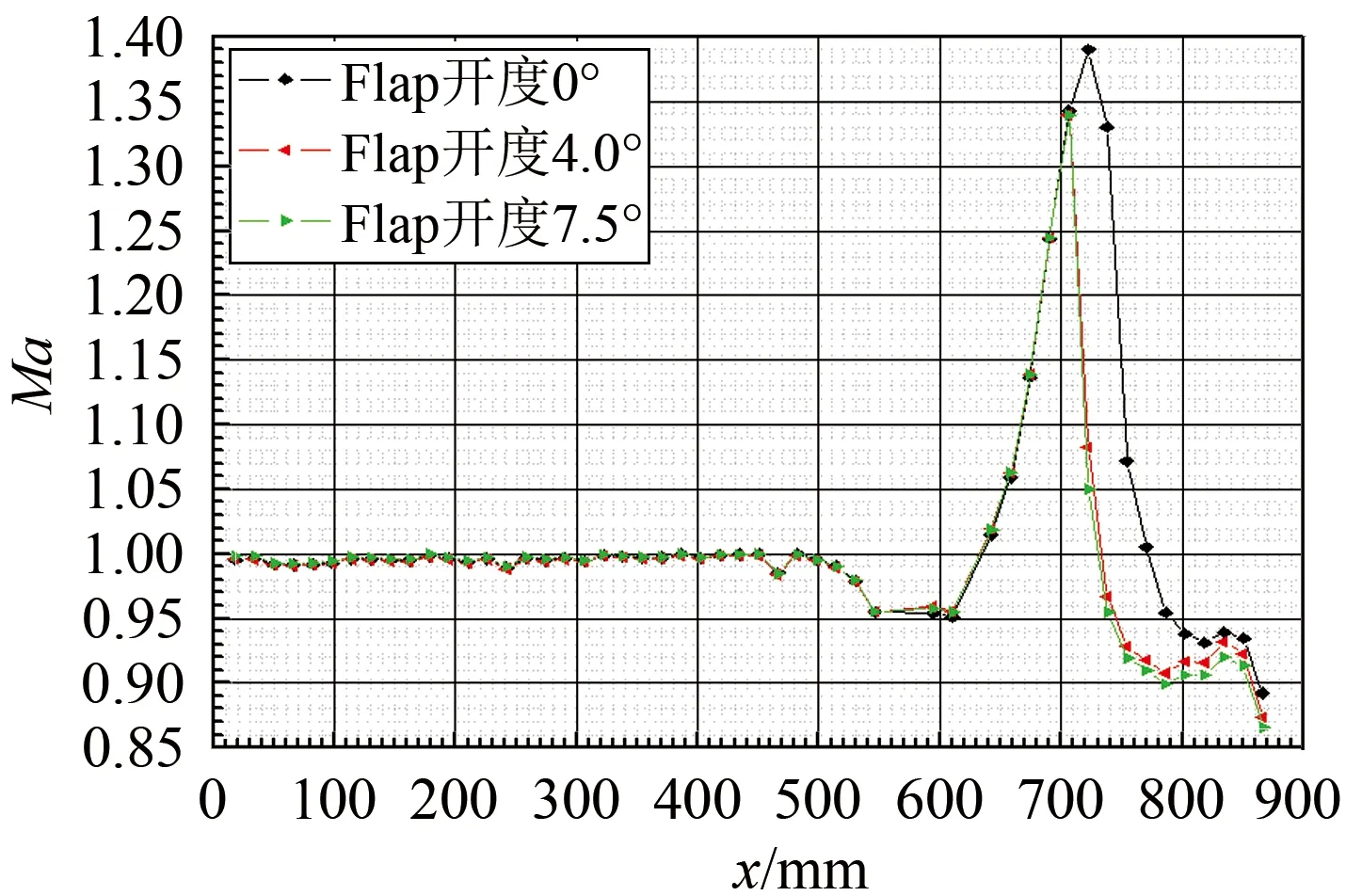
图10 Ma=1.00，0.2 m试验段试验结果Fig.10 The test results of 0.2 m test section at Ma=1.00

(11)

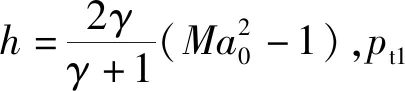
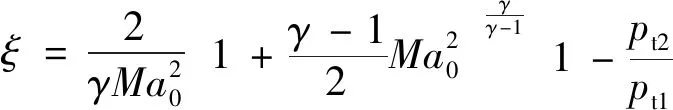
(12)

因此主流引射及激波综合带来的损失系数ξc=0.0672+0.0483=0.1155。

(2) 试验段马赫数Ma=1.10工况

在试验段主流引射的情况下，从Ma=1.00加速至Ma=1.10，加速区长约600 mm(试验结果见图11)，在试验段主流引射的情况下，气动喉道0.8%的排气量将带来额外的总压损失。在支架段，由于支架段扩张使主流进一步膨胀，主流静压进一步降低，对驻室气体起到抽吸作用，同时主流形成激波系，根据0.2 m试验段试验结果，波前马赫数达1.43(见图12)，计入此激波系的损失。

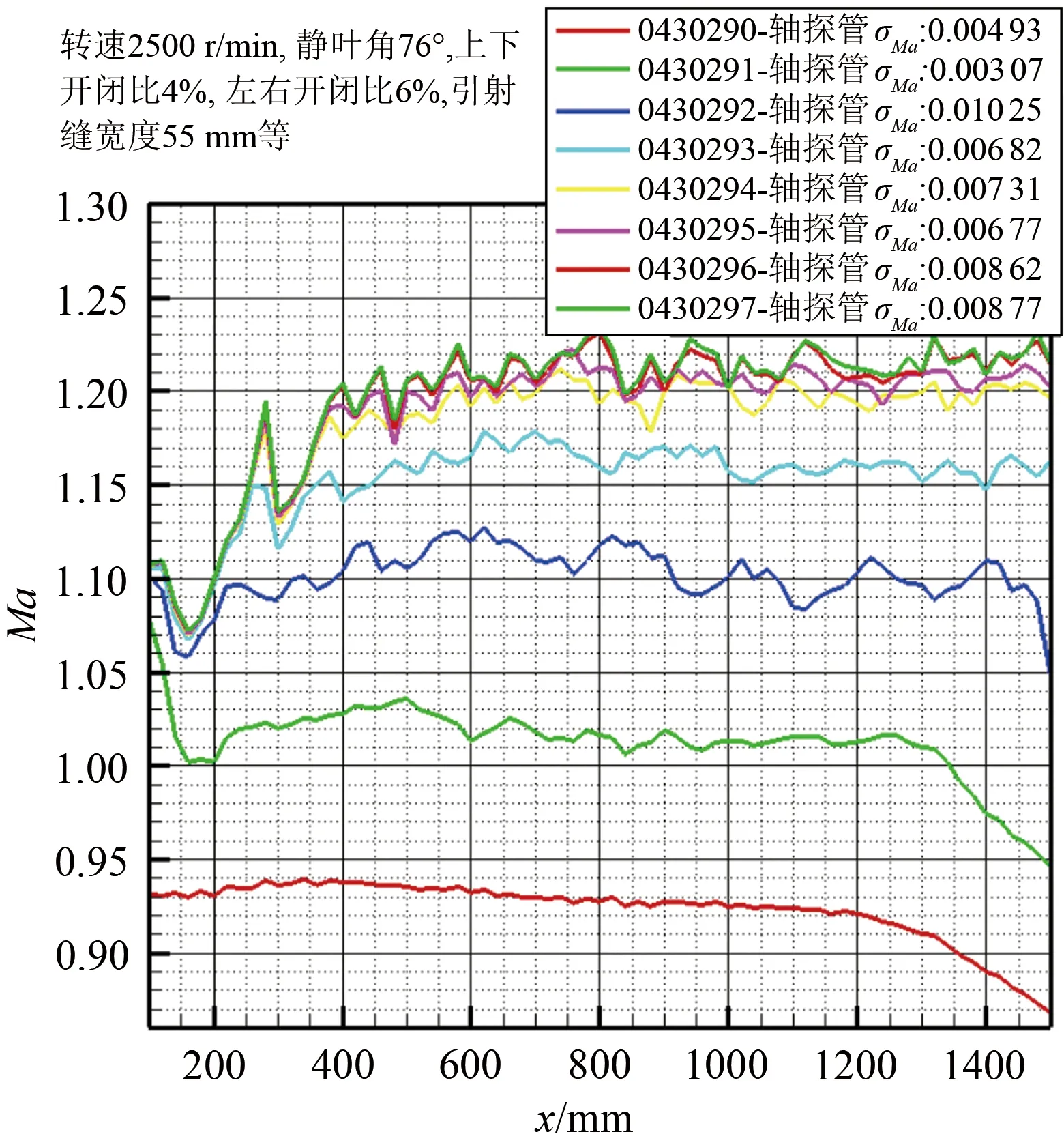
图11 孔壁试验段不同试验车次试验结果Fig.11 The test results of perforated-wall test section

图12 0.2 m试验段试验结果(Ma=1.10)Fig.12 The test results of 0.2 m test section at Ma=1.10

(3) 试验段马赫数Ma=1.20工况

在试验段主流引射的情况下，从Ma=1.00加速至Ma=1.20，加速区长约600 mm，气动喉道3%的排气量带来额外的总压损失；在支架段，由于支架段扩张使主流进一步膨胀，主流静压进一步降低，对驻室气体起到抽吸作用，同时主流形成斜激波系，该激波系前的马赫数近似为1.50(具体CFD计算结果见图13)，因此计入此激波系的损失。

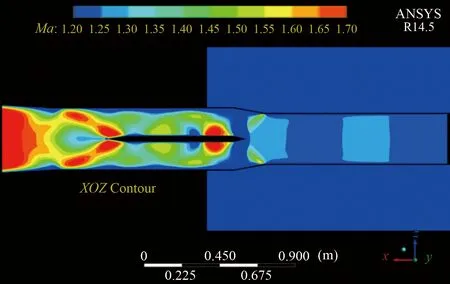
图13 低超声速范围支架段马赫数云图Fig.13 Mach number diagram of model support section with low supersonic range

(4) 试验段马赫数Ma=1.30和1.40工况

在此工况下，实际风洞运行实践表明：单纯在声速喷管下，通过主流引射，试验段出口处膨胀抽吸能力受限，最高马赫速只能达到1.20左右。因此需通过半柔壁喷管，在试验段入口达到Ma= 1.30和1.40的运行工况；在试验段内仅需克服附面层增长带来的影响，再入区再入气体很少，根据CFD计算结果分析(见图14)，Ma=1.30时，试验段再入区最大马赫数为1.75，Ma=1.40时，最大马赫数为1.80，计入相应激波系的损失。

图14 模型支架段马赫数云图Fig.14 Mach number diagram of the model support section

3.1.4 模型支架产生的压比εd

模型支架为支撑模型的弯刀机构，其在风洞中阻塞度较大。吹风过程中会形成较大的尾流区，为风洞增加额外的损失。

中间的模型支架总的阻塞度约为1%，因此模型支撑的扰流损失系数为ξd1=0.041(参考流体阻力手册圆边平板扰流经验公式)[8]。由于中间托板的存在，此处的流阻为两侧管道形成的流阻，支架段长度为1.2 m，主要为摩擦阻力，摩阻系数与雷诺数有关。

(13)

在总温T0=310 K，总压p0=0.1 MPa时，马赫数Ma=1.00下的雷诺数Re=6.692×106，由此可得：λ′=0.009。

基于以上不同部位的损失系数，即可得到试验段的综合损失系数。

3.2 风洞其他部段损失系数

风洞其他部段内部型面相对简单，在流体阻力手册[8]中收录了相似管道不可压缩工况下的数据和计算公式，充分考虑来流条件和自身细节特点，选取相应的拟合和修正公式后，便可得到其他部段的损失系数(见表2)。

表2 风洞各部段损失系数Table 2 Loss coefficient of each part of the wind tunnel

4 风洞压比及各部段参数计算程序

4.1 风洞压比及部段参数迭代计算

高速风洞各部段参数关系式较多，且在计算前，压缩机压升信息、温升信息以及换热器的温降信息等均未知，因此在各段压力损失系数估算完成后，需根据一维管流关系式对风洞流场进行第一次初始化计算，以获得压缩机压比和功率的初步信息。

然后通过初始化后的部段参数，对第二喉道至第一拐角的高速部段进行压缩性修正并计入支架段激波损失，再次计算压缩机压比和功率信息(在计算压缩机出入口压力时需扣除压缩机自身流道的损失，而在计算压缩机功率时应计入此部分损失)。

最后再通过第三次迭代计算，将压缩机的功率转变为出入口的温升信息，纳入到相应部段中。以上每一次计算都对各部段参数重新修订，最终计算出各部段准确的压力、温度、流速等参数信息。计算流程如图15所示。

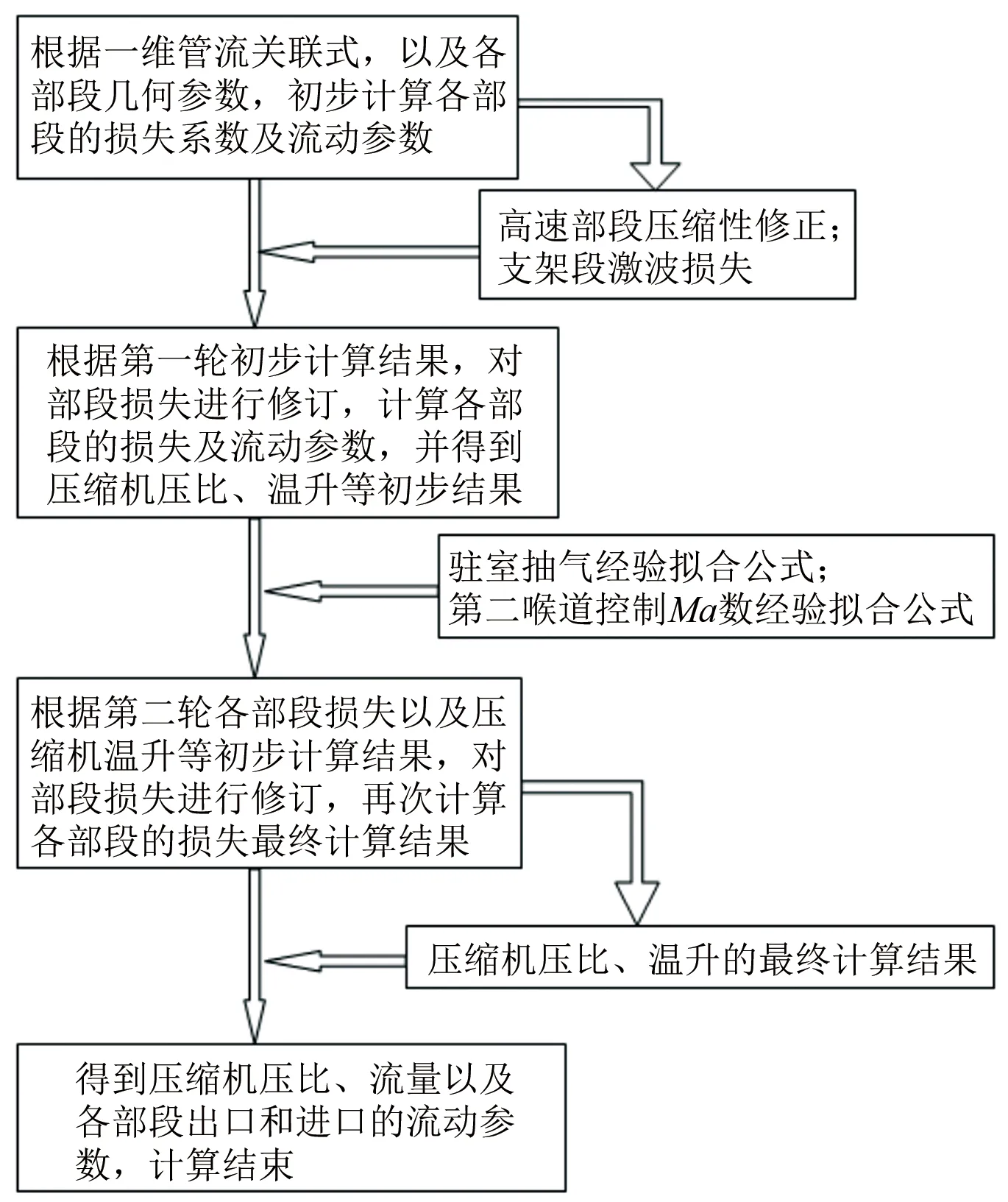
图15 风洞参数计算流程图Fig.15 Flow chart of wind tunnel parameter calculation

4.2 计算结果分析

根据国际上公开资料，关于高速风洞损失估算方面，国际先进风洞——美国NTF风洞在不同马赫数下估算的压比结果与试验测试结果对比如图16所示，在马赫数1.15内，最大偏差达10%。

表3给出了文献统计的不同风洞损失估算方法及偏差汇总，损失估算程序+试验数据结合的半经验方法(Loss program+test data)偏差在10%左右。

图17给出了根据本文估算方法，在不同马赫数下，风洞压比数值估算和试验结果。与试验结果相比，本文计算方法所获得的估算结果在Ma=1.30时偏差最大，最大偏差为7.5%左右，在亚声速及低超声速范围最大偏差均在5%左右，尤其是在Ma=0.80以下的工况，其偏差均在5%以内。

图16 国际同类风洞设计的估算结果[5]Fig.16 Estimation results of similar international wind tunnel[5]

表3 不同压力损失计算方法不确定度汇总[4]Table 3 Accuracy of different pressure loss calculation methods[4]

图17 估算与试验结果对比Fig.17 Comparison of estimation and the test results

5 结 论

通过对跨声速风洞透气壁损失的详细研究，充分考虑了透气壁板和试验段内激波的影响。结合引导风洞的对比验证试验，获得了风洞压力损失估算偏差(7.5%以内)，可为风洞部段结构设计和压缩机选型提供参考。