考虑车流密度影响的驾驶风格识别方法研究*

赵 韩，刘 浩，邱明明，曹龙凯，张义雷，虞 伟

(1. 合肥工业大学机械工程学院，合肥 230009；2. 汽车技术与装备国家地方联合工程研究中心，合肥 230009)

前言

驾驶风格是驾驶员在驾驶车辆过程中的行为特征，体现在开车过程中人对车的输入及整车响应[1]。在整车能量管理策略开发过程中，驾驶风格的有效识别可增强整车对不同驾驶风格自适应能力，这对于提高燃油经济性和降低排放具有重要意义。

在驾驶风格识别方面，国内外学者开展了大量研究。文献[2]中利用人工神经网络将驾驶风格分为非常运动型、运动型、正常型、戒备型和非常戒备型。文献[3]中利用支持向量机、k 最近邻算法、随机森林等方法对驾驶员风格进行了识别，并比较了各种方法的准确度。文献[4]中利用模糊逻辑算法在Matlab/Simulink 中设计了一种在线驾驶风格识别系统。文献[5]中搭建了一种基于数据挖掘和神经网络等人工智能技术的DrivingStyles 软硬件平台。文献[6]中研究了不同性能的轻型汽车对驾驶风格的影响。文献[7]中提出一种双层指针模型，使得驾驶风格识别与车辆所处驾驶环境相结合。文献[8]中搭建了一种用于驾驶行为分析的低成本远程数据采集系统。

国内学者对于驾驶风格的研究起步较晚，但经过十余年的积累也有了一定的成果。文献[9]中利用基于K－means 聚类的支持向量机方法，开发了一种快速模式识别方法，可将该方法用于驾驶风格分类。文献[10]中通过驾驶员的制动特性构建了一套基于隐马尔可夫模型算法的驾驶风格识别方法。文献[11]中从加速与减速两个角度分析驾驶风格并利用支持向量机算法进行了识别。文献[12]中将驾驶风格分为保守型、一般型和激进型，并基于Gini 指数构建了用于驾驶风格识别的随机森林模型。文献[13]中对驾驶风格识别方法在不同车型上的通用性与适应性进行了研究。文献[14]中采用冲击度的标准差结合典型工况下的平均冲击度值来对驾驶风格分类并进行在线识别。文献[15]中采用基于K 均值聚类结果的高斯混合模型对驾驶风格分类。文献[16]中采用基于马尔可夫链蒙特卡洛采样和离群点剔除的K－means 算法对驾驶风格进行分类。文献[17]中提出一种基于标准化驾驶行为和相空间重构的驾驶风格定量评估方法。文献[18]中采用高斯混合分布模型算法对起步工况下的驾驶风格分类。

上述研究中，大多没有考虑车流密度对驾驶风格的影响。为此，本文中从分析车流密度与驾驶风格特征参数之间的耦合关系入手，通过对不同车流密度下的驾驶风格特征参数修正问题展开研究，建立一种考虑车流密度影响的驾驶风格多层次识别方法。

本文中首先以模拟驾驶软件3D Instructor 2 为基础搭建实验平台，采集不同车流密度下不同驾驶风格驾驶员的踏板信号与速度信号，并提取驾驶风格特征参数；然后采用主成分分析法对特征参数进行简化与降维处理，得到不同车流密度影响下的表征驾驶风格的综合特征参数，在此基础上应用减法聚类和K 均值聚类混合算法对驾驶风格进行了分类与特征参数修正；最后采用随机森林算法构建驾驶风格辨识模型，进行模型训练与k折交叉测试验证，并与未考虑车流密度影响的驾驶风格识别方法进行对比，验证在驾驶风格识别中考虑车流密度影响的必要性。

1 实验数据的采集

本文中采用模拟驾驶平台并通过驾驶员在环实验获取实验数据。试验过程中，采用图1 所示的系统实时采集制动与加速踏板数据，采用视觉识别软件提取车速数据。

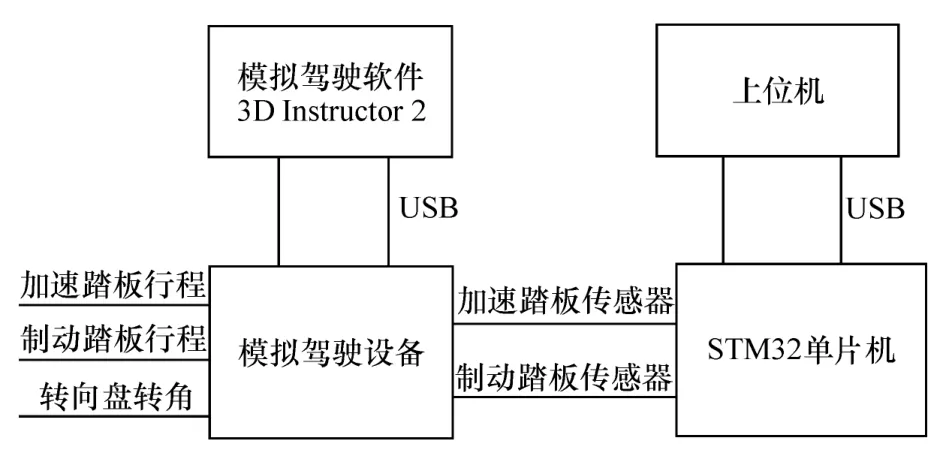
图1 模拟驾驶实验数据采集系统

实验选取城区道路工况进行模拟驾驶实验，路线全长4.7 km，如图2 中A 路径所示。

图2 模拟驾驶实验路线规划

使用3D Instructor 2 软件的车流密度设置选项，设置车流密度分别为10%、40%、70%、100%的4 种城区工况，针对44 位驾驶员，通过驾驶员在环实验，分别在上述4 种车流密度下进行数据采集，共采集有效实验数据176 组(每种车流密度工况下采集44组)，模拟驾驶实验台如图3 所示。

图3 模拟驾驶实验台

根据所获取的实验数据，选取17 个特征参数来表征驾驶风格，具体特征参数及其测试数据如表1所示。

2 基于多层次混合算法的驾驶风格特征参数修正

同一组驾驶风格特征参数在不同的车流密度下会表现出不同的驾驶风格类型，为此需要对不同车流密度下的驾驶风格进行重新定义与修正。本章中提出一种多层次混合算法，第一层基于主成分分析法对驾驶风格特征参数进行综合与降维处理，得到综合特征参数，第二层，采用减法聚类的方法获取不同车流密度下不同驾驶风格的综合特征参数聚类中心，在此基础上通过K 均值聚类方法对上述综合特征参数聚类中心进行修正，计算出修正后的各类驾驶风格特征参数，具体流程如图4 所示。

2.1 基于主成分分析法的驾驶风格综合特征参数提取

表1 驾驶风格特征参数及其测试数据

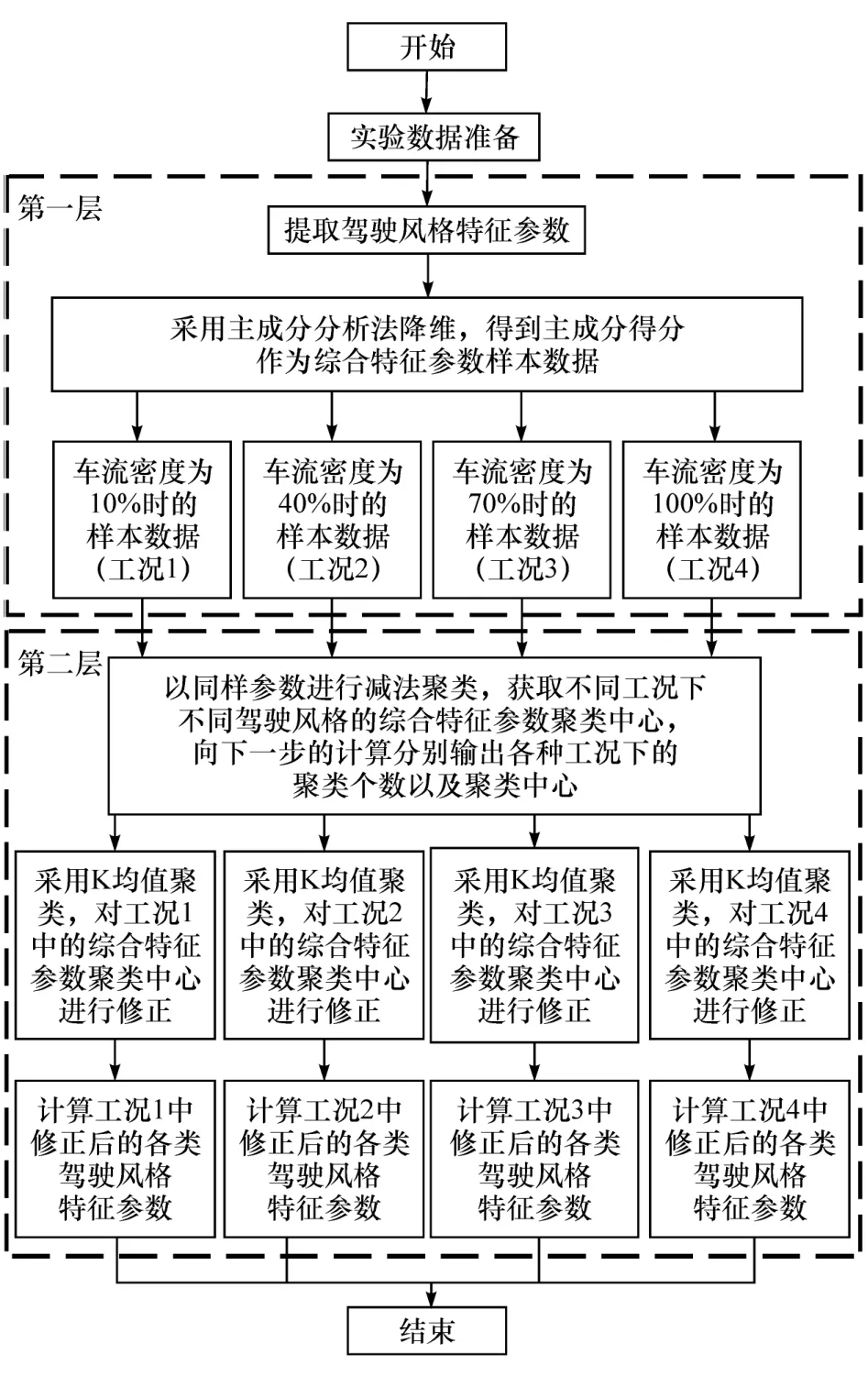
图4 驾驶风格分类计算流程框图

驾驶风格相关的特征参数众多，直接将样本数据用于聚类分析效果较差，且计算和分析过程复杂，因此需要采用主成分分析法[19]对驾驶风格特征参数进行综合和降维处理，建立能综合表征所有驾驶风格特征参数的样本矩阵。

根据上文中所提取的驾驶风格特征参数，进行主成分综合处理，得到17 个主成分，即原始特征参数的17 种组合方式，在此基础上进行主成分分析，得到17 个主成分的贡献率(如图5 所示)和17 个主成分的特征值碎石图(如图6 所示)。

由图5 可知，前4 个主成分的累计贡献率为81.68%。按照累计贡献率大于80%的要求，取前4 个主成分即可表征17 个特征参数的绝大部分信息。同样，由图6 可知，按照特征值大于1 的要求选择前4 个主成分。前4 个主成分的得分如表2所示，根据主成分得分矩阵建立综合特征参数样本矩阵。

表2 主成分得分

2.2 驾驶风格综合特征参数的聚类分析

2.2.1 基于减法聚类的综合特征参数聚类中心提取

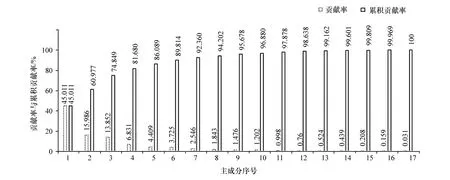
图5 主成分贡献率

图6 主成分的特征值碎石图

本文中采用减法聚类提取综合特征参数样本矩阵的聚类中心，具体算法流程如图7 所示。

图7 减法聚类算法流程

式中ra为该点邻域半径。

式中sf为比例系数。

用于乘以确定集群中心邻域的半径值，从而消除将外围点视为集群一部分的可能性，通过设置参数值可避免聚类中心过于密集的重合聚类问题或者分类不充分导致的欠分类问题。

在样本集确定的情况下，减法聚类得到的聚类中心个数与位置由参数δ与sf确定。本文中提出的驾驶风格分类算法中，通过对比实验，确定参数δ取0.2、sf取1.75 时，驾驶风格能被分割成较恰当的3类，得到4 种车流密度下综合特征参数聚类中心，如表3 所示。

表3 4 种车流密度下的综合特征参数聚类中心

由表3 可知，将4 种车流密度下的综合特征参数样本数据分别使用同样的参数进行减法聚类后得到了相同数量的聚类中心，即在上述各种工况下，驾驶风格均可恰当地被分为3 类。

根据文献[20]和文献[21]，按照驾驶员激进程度的强弱将驾驶风格分为谨慎型、稳健型和激进型。

2.2.2 基于K 均值聚类的驾驶风格特征参数修正

K 均值聚类是一种迭代求解的聚类分析算法，具体流程如图8 所示。

由图8 中所述流程可看出K 均值聚类结果受初始聚类中心的影响较大，如果初始聚类中心选取不当，聚类结果可能会陷入局部最优解。使用减法聚类计算得到的综合特征参数聚类中心作为K 均值聚类的初始聚类中心，可提高算法的自适应性与稳定性，得到较好的聚类效果，迭代停止后得到修正后的综合特征参数聚类中心，如表4 所示，同时得到的聚类结果，如图9 ～图12 所示，其中聚类结果1、2 和3分别表示第1 类、第2 类和第3 类驾驶风格。

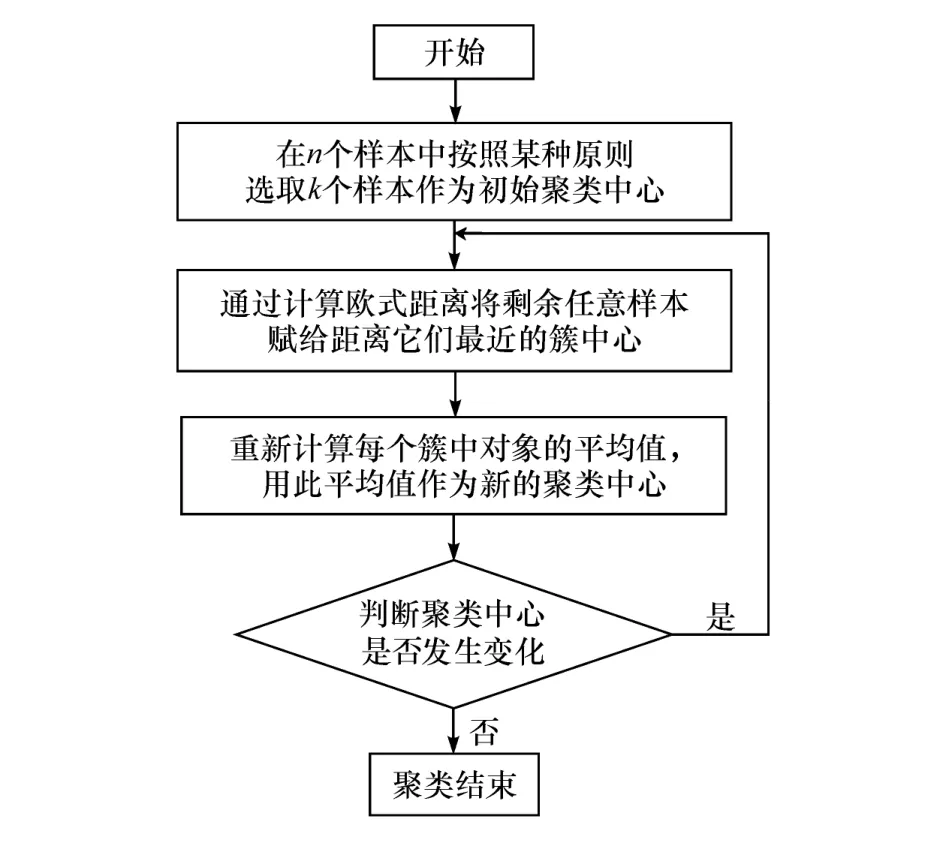
图8 K 均值算法流程

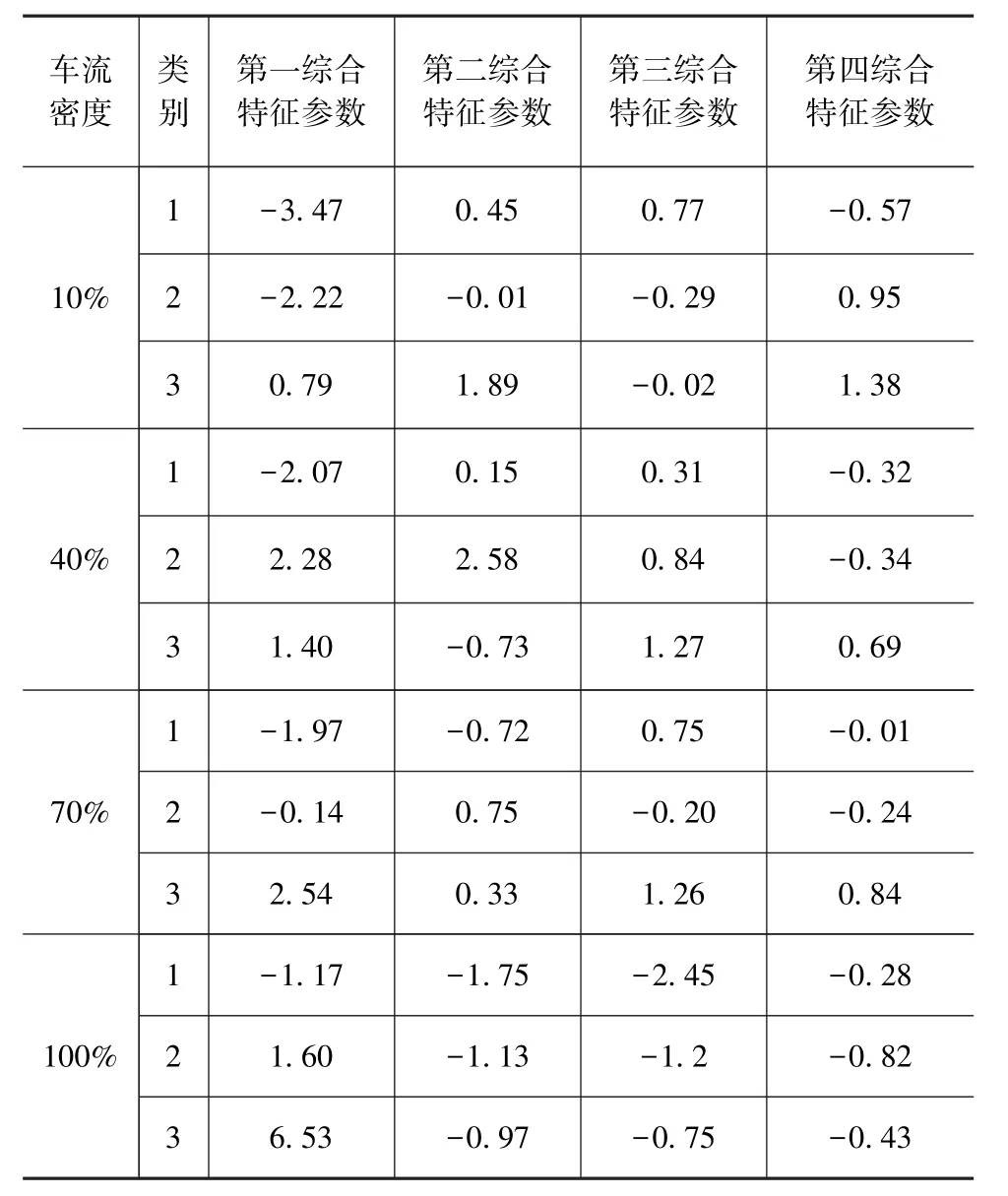
表4 修正后的综合特征参数聚类中心

图9 车流密度为10%驾驶风格聚类结果

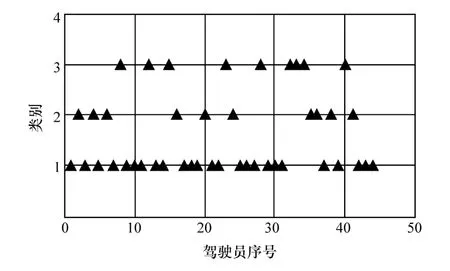
图10 车流密度为40%驾驶风格聚类结果

图11 车流密度为70%驾驶风格聚类结果

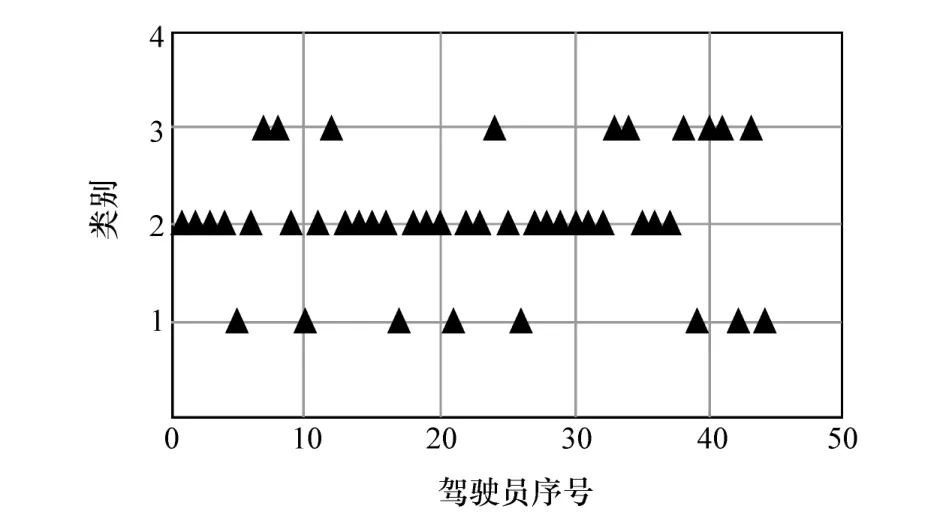
图12 车流密度为100%驾驶风格聚类结果

对聚类后的样本进行计算分析，修正不同车流密度下的驾驶风格特征参数，得到相应的特征参数表，如表5～表8 所示。

由表5 可知，对于车流密度为10%的工况，类别3 为激进型，其各项特征参数的绝对值除加速踏板均值以外均为最大；类别2 为稳健型，与类别1 相比，其车辆加速度波动大、正向加速度大且变化快，加速踏板行程大、变化快且变化速率波动大，制动踏板行程大、变化快且变化速率波动大；类别1 为谨慎型。

由表6 可知，对于车流密度为40%的工况，类别1 为谨慎型，其各项特征参数的绝对值除加速踏板均值以外均为最小；类别3 为激进型，与类别2 相

比，其车速高、正向加速度大且变化快，加速踏板行程大、变化快且变化速率波动大；类别2 为稳健型。

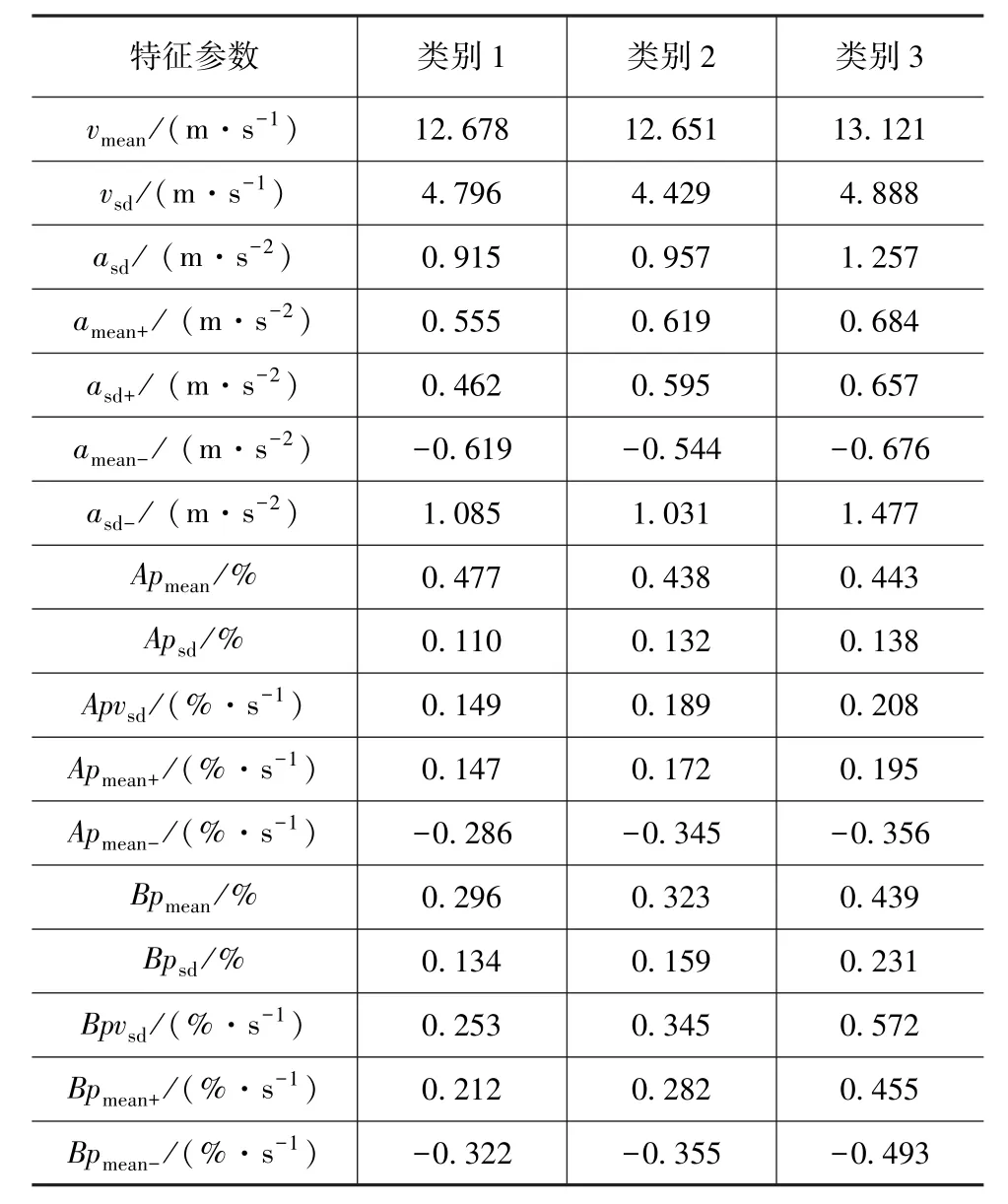
表5 驾驶风格特征参数值(车流密度为10%)

表6 驾驶风格特征参数值(车流密度为40%)

表7 驾驶风格特征参数值(车流密度为70%)

表8 驾驶风格特征参数值(车流密度为100%)

由表7 可知，对于车流密度为70%的工况，类别3 为激进型，其各项特征参数的绝对值除加速踏板均值以外都均为最大；类别2 为稳健型，与类别1 相比，其车辆加速度波动大、负向加速度大且变化快，加速踏板行程变化快且变化速率波动大，制动踏板行程大、变化快且变化速率波动大；类别 1 为谨慎型。

由表8 可知，对于车流密度为100%的工况，从类别1 到类别3，各项特征参数的绝对值都是从小到大，符合谨慎型、稳健型与激进型驾驶风格的特征。

3 基于随机森林算法的驾驶风格识别

在对驾驶风格进行准确表征的基础上，引入随机森林算法构建驾驶风格识别模型。

3.1 驾驶风格辨识模型

对于车流密度为10%的工况，通过聚类分析已得到44 个样本中每一个样本所属的类别，在此基础上构造满足随机森林算法要求的矩阵，其数据如表9 所示。将谨慎型、稳健型和激进型的驾驶风格类别分别记为 1、2 和 3。

表9 用于识别的驾驶风格特征参数(车流密度为10%)

随机森林模型训练原理如图13 所示，具体实现流程如图14 所示。利用图14 所述方法训练得到随机森林模型进行驾驶员驾驶风格识别。

3.2 测试验证分析

采用k折交叉验证的方式对上述驾驶风格识别模型进行测试验证，具体流程如图15 所示。

图13 随机森林模型训练原理

图14 随机森林模型具体实现流程

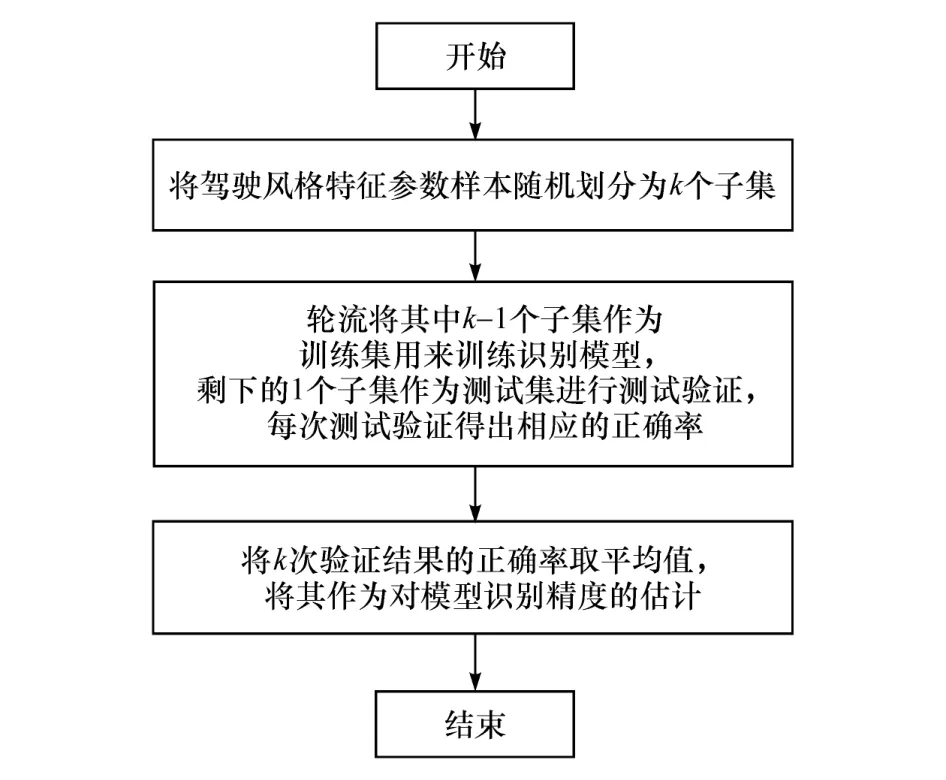
图15 k 折交叉验证具体流程

对于车流密度为40%、70%和100%的工况分别采用上述随机森林算法建立驾驶风格辨识模型并进行测试验证，4 种车流密度下k折交叉验证的测试结果如图16～图19 所示，各个车流密度下驾驶风格辨识模型的识别精度如表10 所示。

图16 辨识模型测试验证结果(车流密度为10%)

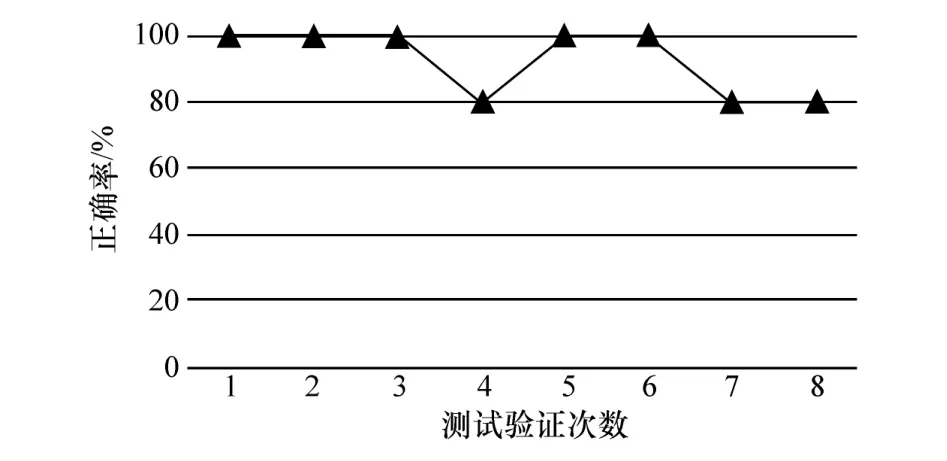
图17 辨识模型测试验证结果(车流密度为40%)

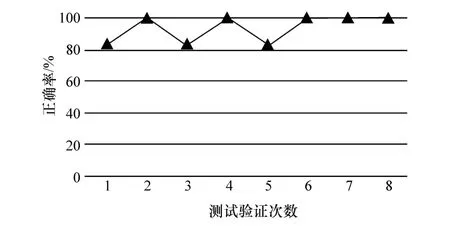
图18 辨识模型测试验证结果(车流密度为70%)

图19 辨识模型测试验证结果(车流密度为100%)

从表10 中可以看出，在4 种车流密度下驾驶风格辨识模型的识别精度都较高，可有效辨识驾驶风格类型。

表10 4 种车流密度下的模型识别精度

从图16～图19 中可以看出，与车流密度为10%和100%的测试验证结果相比，车流密度为40%和70%的驾驶风格识别模型测试验证得到的正确率值普遍更大，且曲线波动更小。这是由于在道路畅通与道路严重拥堵的工况下，不同驾驶风格驾驶员踩踏踏板的信号相似，因此提取的驾驶风格特征参数差异性很小，导致模型识别精度相对较低。

3.3 未考虑车流密度影响的驾驶风格识别

为验证本文中所述方法的优越性，采用车流密度为70%试验数据训练驾驶风格识别模型，然后用该模型对车流密度为10%、40%和100%的实验数据进行测试，得到的模型识别结果如表11 和图20所示。

表11 未考虑车流密度影响的模型识别精度

图20 未考虑车流密度影响的模型识别精度

从表11 与图20 中可见，使用固定的驾驶风格识别模型对不同车流密度对应工况的适应性较差。

4 结论

(1)通过模拟驾驶实验采集了不同车流密度下不同驾驶风格驾驶员的驾驶数据并提取特征参数，采用主成分分析法实现了对特征参数的降维和简化处理，从而得到相应的综合特征参数。在此基础上基于减法聚类和K 均值聚类混合算法对驾驶风格进行了分类与特征参数修正，建立了不同车流密度下的驾驶风格特征参数表。

(2)采用随机森林算法建立驾驶风格识别模型，在此基础上对不同车流密度下的驾驶风格进行识别，并与未考虑车流密度影响的驾驶风格识别方法进行了对比。结果表明，在不同车流密度影响下，本文中所提出的方法驾驶风格识别有效性更好。

(3)建立了多层次混合算法，通过对不同车流密度下的驾驶风格特征参数修正以及基于随机森林算法的驾驶风格识别，使驾驶风格的分类与识别更加细化，可构建一套考虑车流密度影响的驾驶风格识别方法，并能将其应用于混合动力汽车的控制策略优化中，从而为考虑车流密度影响的驾驶风格自适应控制策略的开发奠定基础。