球形轮组结构及其控制系统设计*

翟建丽，莫浩明，曾德胜，周 杰，王可涵，陆厚霖，胡恰锋，王作桓

（广东工业大学华立学院，广州 511300）

0 引言

轮式移动作为运输工具的主要形式，其制造简便和价值成本低，而球形轮组具有灵活性、占地面积小、易于搬动，可以运用在代步工具、机器人和危险地带运输等。国内外为此做了大量研究，球形轮组结构最早应用在机器人中。2006年美国卡内基梅隆大学将球形轮组结构运用在BBR机器人[1]；2008年日本东北学（TGU）采用3 个全向轮结构驱动技术和2010年苏黎世理工联邦理工学院开发了类似于TGU 的原型，具有较高的鲁棒性[2]；2019年加州大学圣地亚哥大学对BBR机器人的机械设计、动态分析等[3]；2012年同济大学的单球机器人建模和控制[4]；2014年以阮晓钢为首对独轮机器人进行自抗扰研究[5]。

本文根据球形轮组的工作原理和自身存在的非线性、强耦合和欠驱动等问题进行研究。利用三维建模软件建立物理模型进行动力学分析，设计控制算法与ROS 系统建立的上位机联合，利用注模技术建立样机对球形轮组进行研究。

1 球形轮组设计

1.1 机械结构设计

球形轮组由3 个全向轮、球轮和车身组成，车身上搭载电源、监测系统、控制系统和执行系统等部分构成，如图1所示。全向轮通过联轴器直接与电机连接，控制电机的力矩间接控制全向轮在球轮上的转速和方向，机身由两层构成，在顶层用于固定电源和主控板，主控板包括控制模块和监测模块；底层用于固定与全向轮直接连接的电机。

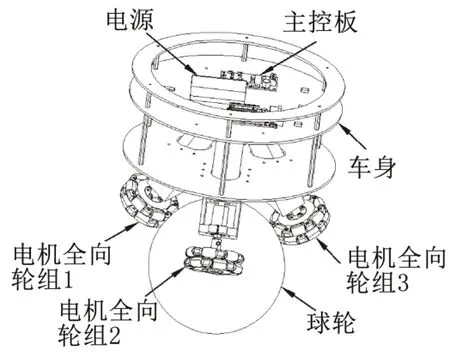
图1 物理模型设计图

当全向轮组受到外界干扰时，3个全向轮通过驱动球轮朝倾斜方向运动来维持自身平衡，俯视图下与电机相连的3个全向轮两两相互成120°，因此通过控制电机的力矩调整全向轮的转速和方向，俯视图下全向轮分布简图如图2所示。

图中，vr1,vr2,vr3分别为3个全向轮的速度，v为某一时刻的速度，根据公式推导出3个全向轮的速度和某一时刻的速度关系式如下所示：

式中：vr1～vr3为全向轮1～3的速度；v为某一时刻的速度。

球形轮组通过利用MPU6050陀螺仪传感器监视机身的姿态变化，并进行处理后传入给控制模块，及时做出反应去调整电机的转速和方向。球形轮组在平面上的运动速度与全向轮速度的关系，在xy平面内的运动简图如图3所示。

图2 全向轮分布简图

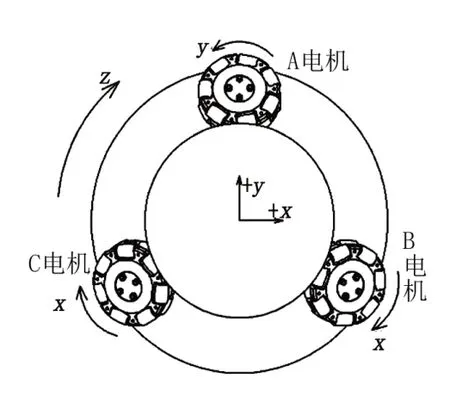
图3 运动简图

根据简图和公式推导出如下的速度关系式：

式中：ω为轮组的角速度；L为全向轮的中心与底盘的中心距离；vA、vB、vC为3个全向轮的转速；vx、vy为球形轮组在x、y方向的运动速度。

1.2 电气设计

球形轮组为了保证自身姿态平衡的同时，保证在平面内任意方向移动，其电气部分需要包括电源、监测、控制和执行部分——电机。电源是为各设备提供稳定的电压，另外需要考虑到整体的重量和体积，因此需要选择重量轻和体积小的电源。因此采用12 V的锂电池作为总电源，分别通过电机驱动和电压转换器提供相应电压给电机、控制系统和MPU6050陀螺仪传感器等。

监测系统采用陀螺仪传感器可以实时监测球形轮组的姿态变化和速度变化；控制系统中采用STM32 芯片，可以根据监测系统采集的数据进行计算处理获得直流电机的控制变量；执行系统根据控制部分的控制变量去控制电机的扭矩。

根据球形轮组的机械结构与电气部分的设计，利用注模技术建立试样机的机身，根据图1 的设计图设计的试样机如图4所示。

图4 实物图

图5 物理模型简图

2 动力学分析

球形轮组是一个多刚体机械结构，非线性、强耦合和欠驱动，为适应自身的自平衡，需要设计一套控制算法。在设计控制算法前需要先进行动力学分析，因为与外部环境接触受到干扰，需要根据控制部分的控制变量来控制电机的力矩，所以需要考虑球形轮组的电机驱动扭矩与驱动轮的力和力矩。球形轮组属于多刚体结构，因此采用拉格朗日方程对球形轮组的动力学分析，可以不考虑刚体内部的关系，同时把球形轮组分成全向轮、球轮和机身三部分。如图5 的物理模型简图所示，由于球形轮组是一个质心高于支点的特征，在自身重力作用下无法保证球形轮组的自身平衡。根据全向轮与球轮和电机的电机关系，有利于非线性控制算法的设计，其拉格朗日方程[6]为：

式中：T为系统总动能，W为系统总势能。则：

通过拉格朗日方程建模和分析，得到电机在球轮上的力矩为：

3个电机的实际力矩为：

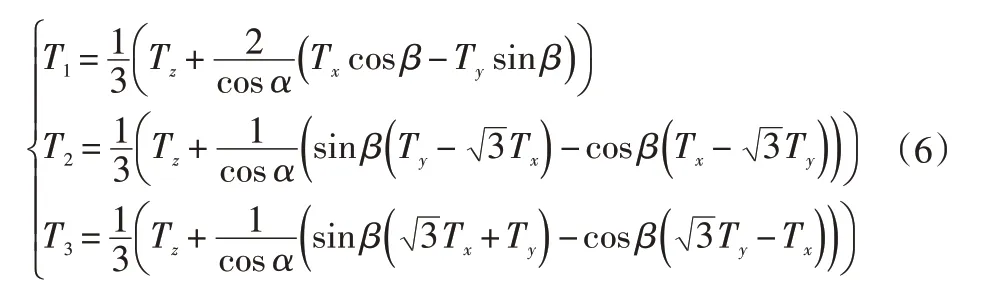
式（3）～（6）中：T为总动能；W为总势能；下标b、w、a分别为球轮、全向轮、机身；Tb为电机在球轮上的力矩；rw为全向轮半径；T1、T2、T3分别为3个电机的实际力矩。

依据刚体力学分析，部分零件不受到力的影响或者可以在球轮组内实现力系平衡，可以不考虑到整体运动中去，所以机械结构简化后得到如图5所示的物理结构简图。

3 控制系统

3.1 控制算法

球形轮组的控制主要包括自平衡控制与位置控制，采用两个相同的LQR状态反馈控制器分别对单球自平衡移动机器人等效的两个一级倒立摆进行自平衡控制与位置跟踪控制[7-8]。

理想情况如下：

（1）全向轮不与球面打滑，同时球面有足够摩擦力；

（2）电机轴线中心正是底盘重心；

（3）各轮之间是绝对的互成120°安装；

（4）电机轴线中心正是底盘重心。

软件控制流程如图6 所示，小车上电后，系统模块进入初始化，系统进入当前状态平衡点采集，采集完后进入系统5 ms 中断服务函数，进行姿态数据采集和逆运动学计算，从而控制直流电机让球形轮组处于动态平衡，系统不断地进行5 ms 中断从而进行小车姿态识别。其中姿态采集需要用到滤波算法才可得到稳定的姿态数据。滤波部分分别通过低通和均值滤波处理加速度计和陀螺仪的原始数据，然后通过互补滤波实现两个数据的融合，从而获得俯仰角和侧倾角数据。

部分控制算法如图7所示。

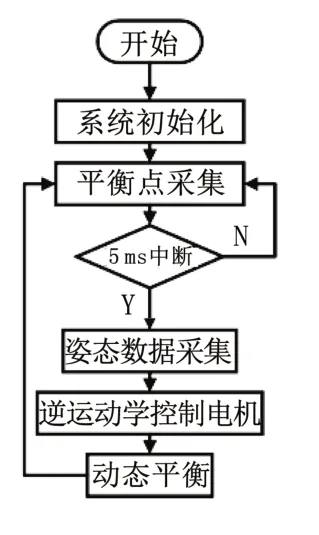
图6 控制算法流程图

图7 部分核心代码

3.2 控制系统

球形轮组的控制系统用来接收MPU6050陀螺仪传感器获取的姿态信息以及上位机发送的控制信息，最后根据所编写的控制算法求出在某一时刻的状态所对应的电机控制量。球形轮组的研究采用ARM公司的STM32F103ZET6芯片，其最高工作频率为72 MHz，FLASH 为512 k 和32 位的CPU，具有丰富的I/O接口、库函数和开源代码，因此开发容易，并满足球形轮组底层平衡控制的要求。

根据图8 的硬件框图所示，MPU6050 陀螺仪传感器采集轮组姿态数据并经过卡尔曼滤波处理后输入到控制系统ROS，然后与姿态平衡点的条件进行比较，MCU 根据姿态偏离程度向电机驱动发出纠正信号，驱动步进电机进行动态平衡调节。

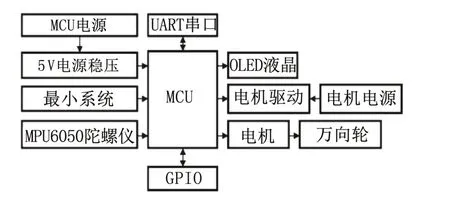
图8 硬件框图

如图9 所示，在MCU 上搭载好ROS 系统，在ROS 中输入ifconfig命令查询小车的IP地址，确保上位机控制端与小车是处于同一局域网下。接着修改控制端的bashrc 配置文件，把小车IP地址填入。因为小车是作为ROS的主节点，所以需要修改export ROS_MASTER_URI的地址为小车IP地址。完成上述步骤后，通过SSH 连接ROS 小车。可以用命令rosrun rviz rviz查看小车的rviz运动方向。用上位机控制小车运动和实时PID调参，如图10所示。

图9 rviz运动状态查看

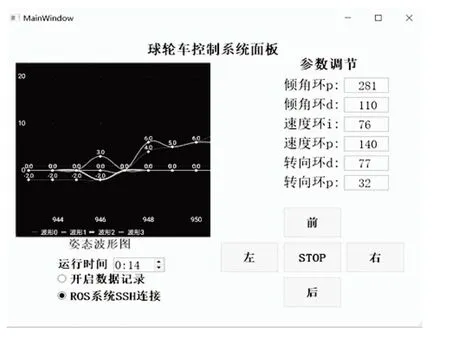
图10 控制系统界面

4 仿真结构

结合上述对球形轮组软、硬件的设计和分析，需要验证其自平衡和控制系统的可实验性。首先将建立的物理模型导入仿真软件MATLAB 中，并结合串级PID控制的对应参数设置进行仿真性试验，得出如图11 所示的仿真对比实验结果。由图可知，球形轮组的姿态角与平衡值发生偏离时，控制模块能够及时接收到传感器传送过来的姿态数据与串级PID 控制算法结合计算出电机的控制变量，迅速改变电机的扭矩来调整相应全向轮转动速度和方向，保证自身的平衡，但是不能保证与理想条件的平衡点相重合，因为研究过程中属于一个理想条件下，没有考虑到能量方面的损失。

图11 仿真实验

5 结束语

针对轮式移动运输工具的不灵活性、占地面积大、不易于搬动的问题，本文提出了球形轮组结构和控制系统的设计，实现球形轮组无转弯半径并且灵活地运动。采用拉格朗日方程进行动力学分析，设计出结构最佳的球形轮组，推出电机扭矩与3个全向轮在球轮上的运动关系，据此设计出拥有倾角环、速度环、转向环的串级PID算法，同时设定好PID参数的初始值。本文提出运用ROS 系统建立上位机实现人机交互，让用户时时刻刻能监控轮组的姿态并做出调整，同时进一步完善PID参数设置。仿真试验验证了串级PID对球形轮组自平衡控制的可行性。

最后针对球形轮组自平衡的实验与实地测试，证明了拉格朗日力学分析的方法能更直观地分析球形轮组物理结构与刚体力系划分；ROS上位机在调试PID的方面具有快速反应、实时监控、简化调试的优点。两种方法互补，把抽象的物理力学平衡用程序实现，为此类复杂繁琐的调试做出了系统的实施方案。