基于Abaqus的土工袋数值模拟算例分析

章致远

（江西省高安市水利局，江西 高安 330800）

近年来，有关土工袋技术在系统性理论研究、定量化分析计算、数值建模与预测以及大规模现场试验等方面取得长足进展。Recio J和OumeraciH[1]研究了采用土工充砂袋铺筑的海岸结构在稳定水流作用下的有效变形问题，并基于实验室研究成果提出了土工袋技术砌筑结构的水力特性及相应概念模型。Hornsey W P等[2]人详细研究了土工袋技术在海岸防护系统中稳定性、耐久性和土工袋的寿命周期等问题及其在澳大利亚的实际应用。Corbella S等[3]介绍了土工织物充砂袋在南非的应用以及研究成果。高存贵等[4]提出了土工袋技术施工过程中的控制、检测要求，并总结了土工袋技术的优点；陶同康等[5]通过理论分析和试验研制了低价高摩擦性能的土工袋；刘斯宏[6～12]等人在土工袋力学性能研究的基础上，采用土工袋技术治理南水北调工程输水总干渠的膨胀土边坡，深入分析了土工袋处理膨胀土的机理，为膨胀土处理开辟了新途径。

目前针对土工袋的有限元分析方法主要有整体式、分离式两种型式。前者是将袋子的张力作用等效为附加应力作用在土骨架上，并将土体单元视为连续均匀的材料，这种方法无法揭示袋子与土之间相互作用的机理[13]；后者主要将土体单元与袋子分开采用不同的单元模型，各自划分为单元，引进接触面单元实现模拟，采用这种模拟方法模拟多个土工袋时计算量巨大[13，14]。

采用有限元方法模拟土工袋涉及到土体和袋子单元的选取、土—袋子、袋子—袋子、袋子—结构物之间的接触设置、土体本构的选择等问题。下面结合前人研究成果与有限单元法元理论从模拟软件介绍、土体本构、袋子单元、接触分析和算例计算5个方面概述土工袋有限元数值模拟。

1 Abaqus软件概述

Abaqus是一款功能强大，操作便捷，适用性广的有限元软件。目前该软件已经被广泛应用于岩土、水利工程的数值计算中，有效性得到了实际工程的验证。Abaqus有限元软件拥有众多单元库与模型库，可以解决岩石力学、固体力学等不同领域的问题，特别是在非线性分析领域，可以解决复杂的工程实际问题，融结构、传热学、流体以及热固耦合、流固耦合于一体，具有驾驭庞大求解规模的能力。

2 土工袋模拟方法

在进行土工袋有限元计算分析时，涉及袋内材料的本构模型、土工编织袋的模拟及土工袋层间接触模拟等问题。受到袋内材料和袋子材料的影响，土工袋呈现出的变形规律也各不相同。因此，在进行土工袋有限元计算时，应根据袋内材料特性和袋子特性分别选取合适的计算参数。

2.1 本构模型

土的本构模型是影响有限元计算结果的一个重要因素[15～17]。土体变形影响因素很多，规律非常复杂。对于细砂材料，工程中常用邓肯-张模型进行有限元计算分析。对于本项目使用的灰渣，在进行有限元计算分析时，工程中则常用Mohr-Coulomb弹塑性模型。

2.2 土工编织袋模拟方法

土工编织袋可以有两种模拟方式：一种是将土工袋组合体简化为一个等效的加筋土体；另一种是用杆单元模拟土工编织袋，袋子与袋中材料单独模拟。

2.2.1 用组合体模拟土工袋

将土工袋组合体简化为一个等效的加筋土体，加筋土体的抗剪强度中考虑袋子张力引起的附加凝聚力。由式（1）计算得到：

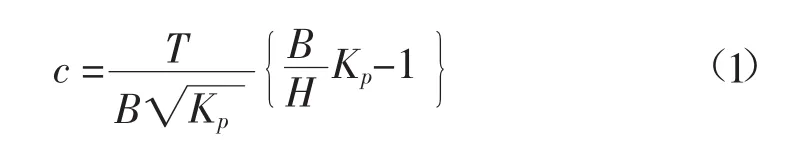
式中：c为粘聚力，kPa；T 为温度，℃；Kp为被动土压力系数；H为水头，m；

2.2.2 用杆单元模拟土工袋

土工编织袋具有能抗拉，但不能抗压、弯、剪的普遍特性，可采用线弹性的杆单元进行模拟，杆单元的劲度矩阵累加到整个土体结构的整体劲度矩阵中。当杆单元处于受压状态，则不计该杆单元的劲度贡献。

2.3 土工袋层间接触模拟

在结构物中，如果两种材料性质相差很远，在一定的受力条件下有可能在其接触面上产生错动或开裂[7]。在土工袋组合体中就存在这样3种形式的接触面：袋子与袋子之间、袋子与结构物之间以及袋内材料与袋子之间的接触面，这时可设置接触单元进行模拟。本项目拟采用Goodman无厚度接触单元进行模拟。

3 土工袋有限元分析算例

3.1 计算参数

为模拟该实际工程，选择大土工袋尺寸为1 000mm×800mm×400mm（长×宽×高），小土工袋尺寸为500mm×800mm×200mm（长×宽×高），与设计采用的土工袋一致。在计算中土工袋的力学参数取用见表1，土工袋内装砂的物理力学参数取自拉姆火电厂地区的地质工程勘探表（见表2）。

根据表2中土体的物理力学参数，结合以往工程经验，选取邓肯张模型的参数见表3。

计算过程中忽略编织袋与土体的接触，只考虑袋子与袋子的接触。为模拟编织袋之间的相互作用，在两者之间设置无厚度的Goodman接触单元，接触面的参数如表4。

表1 黑色PP编织袋的性能指标

表2 拉姆火电厂区域砂的物理力学参数

表3 拉姆火电厂区域砂邓肯张模型参数

表4 接触面单元参数

3.2 土工袋在ABAQUS中的模拟

算例中土工袋的模拟是根据实际工程中建议的大土工袋尺寸建立的模型，长度为100cm，高度为40cm。本次计算中用平面应变单元模拟砂，用仅受张拉的杆单元和等效加筋两种方法分别模拟土工袋。假设砂土和编织袋之间结合完好，砂土—编织袋之间不设置接触单元，而在编织袋交接处设置接触面单元。

3.3 土工袋无侧限压缩试验模拟

土工袋无侧限压缩是对两个上下堆叠的土工袋组合体施加竖向荷载，计算过程中在土工袋上、下方设置刚性加载板且约束下方加载板的位移和转动。加载板表面积远大于土工袋上、下表面，故忽略土工袋自重对压缩的影响，将上层土工袋自重对下层土工袋的影响转化为均布力施加在下土工袋顶部。为了模拟土工袋上部荷载的施加过程，计算中共分为10级加载，最后竖向荷载达到100kPa。

3.3.1 杆单元法有限元模型

土工袋模型由1 136个单元、1 034个节点组成，其中杆单元100个，接触面单元120个，如图1所示。图中点V1～V6和H1～H6为位移监测点。

3.3.2 等效加筋法有限元模型

采用等效加筋法进行土工袋模拟时，袋子张力的约束作用增强了内部土颗粒间的接触作用，相当于在内部颗粒间增加了一个附加粘聚力。根据前述的土工袋强度原理，单个土工袋的凝聚力可以按式（1）计算：

图1 土工袋网格模型图

等效加筋法模拟土工袋的模型仍由1 136个单元组成，如图2所示。图中点V1～V6和H1～H6为位移监测点。

3.3.3 计算结果对比分析

图2是典型节点在加载过程中竖向位移与荷载的关系图。从图2（a）中可见，典型节点的竖向位移随荷载增加均呈现变大的规律，且基本呈线性分布。由于底部无位移，靠近底部的典型节点竖向位移几乎为0；越靠近顶部，位移越大。最大位移出现在靠近顶部的V1节点，为-2.48cm。图2（b）中各典型节点位移变化与图3（a）基本一致，最大位移同样出现在V1节点，为-2.79cm，略大于杆单元法。

图3是典型节点的水平位移与荷载的关系图。从图中可见，由于模型对称加载，水平位移呈两两反对称的形式。在荷载作用下，土工袋两端水平移动较为明显，说明土工袋向两端伸展，最大水平位移分布在每层土工袋中部，分别向上下两侧减小，方向均朝土工袋外侧。两种方法计算中等效加筋法的位移差值较小且略大于杆单元法，其中杆单元法典型节点最大水平位移出现在H2与H4，为-3.99cm；等效加筋法中典型节点最大水平位移也是H2与H4，为-4.55cm。

图2 典型节点的竖向位移和加载关系

图3 典型节点的水平位移和加载关系

图4 加载后的位移矢量图

图4绘制了加载后袋内土体的位移矢量图，由于模型具有对称性，故计算结果亦呈现出良好的对称性。从图4中可以看出，土工袋在外荷载作用下，整体发生压缩变形，袋内土体在土工袋受压过程中向四周移动，具有明显的向两侧鼓出的趋势，土工袋逐渐变成扁平状，袋子周长变长，该趋势必然受到编织袋的约束，限制其变形，从而在编织袋内产生张力，这与实际中的土工袋受力变形情况完全一致。相比之下，等效加筋法的结果偏大，这是由于杆单元模拟的袋子对袋内土起到约束作用，限制了其位移。

3.4 土工袋水平剪切试验模拟

土工袋水平剪切试验是对两个上下堆叠的土工袋组合体施加水平剪切力，计算过程采用刚性板加载法。在下方土工袋底部和左部设置刚性板并约束位移和转动，忽略自重对压缩的影响，将上土工袋自重对下土工袋的影响转化为均布力施加在下土工袋顶部。为了模拟土工袋荷载的施加过程，模型顶部施加100 kPa的竖向均布力，对上土工袋施加从右向左的水平推力，计算中共分为10级加载，最后水平荷载达到50kPa。

（1）杆单元法有限元模型。土工袋模型由1 136个单元组成，如图5所示。图5中点V11～V62和H1～H6为位移监测点。

（2）等效加筋法有限元模型。土工袋模型由1 136个单元组成，如图5所示。图中点V11～V62和H1～H6为位移监测点。

图5 土工袋网格模型图

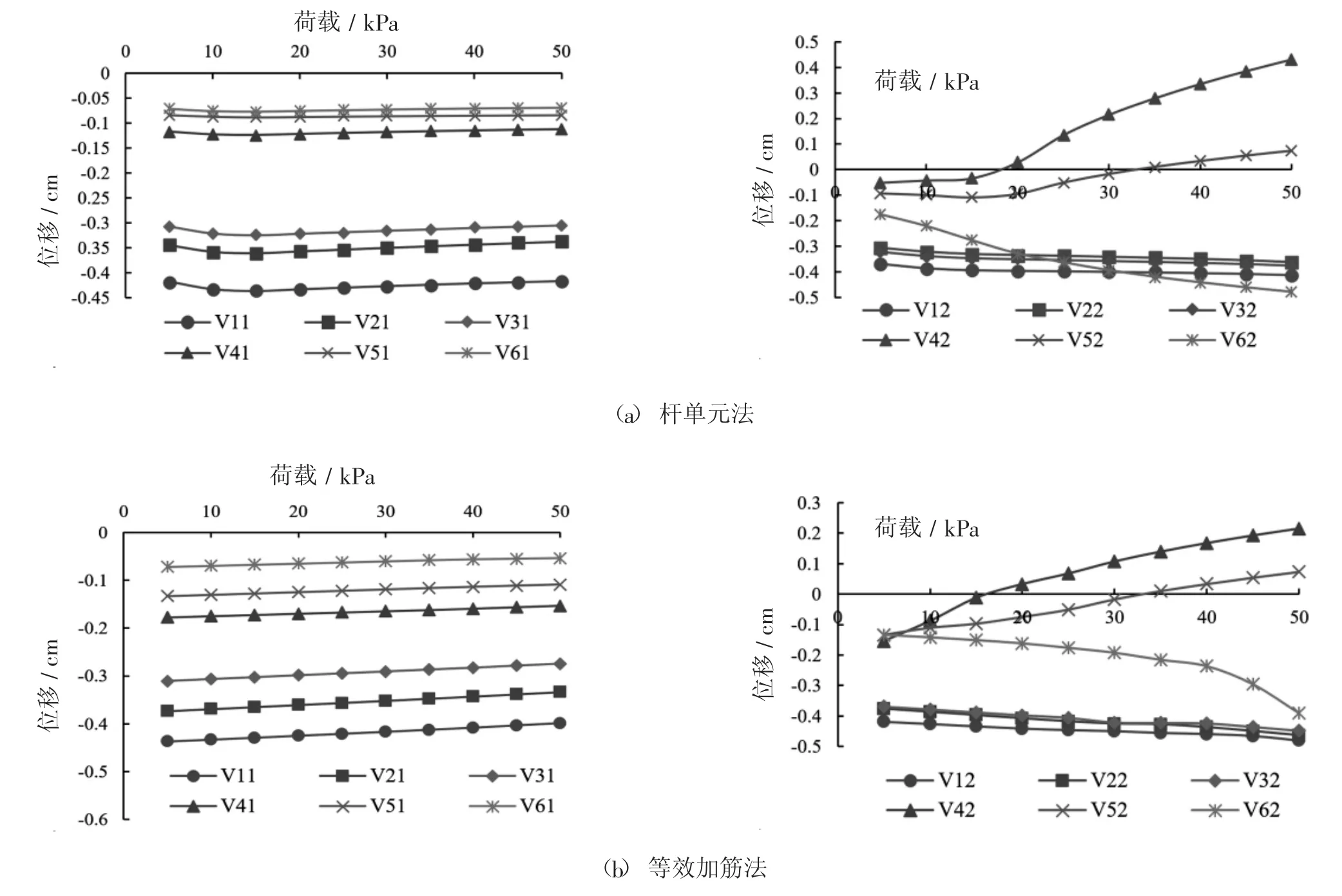
图6 典型节点的竖向位移和加载关系

（3）计算结果对比分析。图6是典型节点在加载过程中竖向位移与荷载的关系图。从图6（a）中可见，土工袋右侧的典型节点竖向位移随着水平荷载的增加逐渐减少。这是由于在加载过程中，随着水平荷载的增加，土工袋受层间摩擦作用，上层土工袋右侧竖向位移总体呈现随荷载减小的趋势。土工袋左侧典型节点竖向位移变化与右侧不同，下层袋子会向左侧刚性板移动。上方土工袋变化随水平推力小幅增加，下方土工袋由于设置了左侧挡板，袋内土体向上下发散。总体而言，土工袋的变形基本上与加载的大小成正比，当水平荷载达到50kPa时，土工袋右侧竖向最大位移出现在顶部的V11节点，为-0.42cm，左侧竖向最大位移出现在上方土工袋底部的V12节点（由于下方土工袋袋内土体发散，不考虑其规律性），为-0.41cm。图6（b）中各典型节点位移变化基本与（a）一致，右侧最大位移同样出现在V11节点，-0.40cm，左侧竖向最大位移出现在顶部的V12节点，为-0.48cm。

图7 典型节点的水平位移和加载关系

图7是典型节点在加载过程中水平位移与荷载的关系图。从图7中可见，随着水平推力的增大，土工袋典型节点的水平位移先向右逐渐减小后向左逐渐增大，下层土工袋水平位移变化速度慢于上层土工袋，说明上下层土工袋之间产生相对滑动。加载初期，水平荷载相对竖向荷载作用小，土工袋仍表现为向外伸展，随着水平力的增加，土工袋开始沿剪力方向移动。由于底部及左侧设置刚板，故加载初期土工袋底部水平位移较大，且变化速度最慢。从图7（a）和图7（b）计算的结果对比来看，杆单元法和等效加筋法计算结果也保持高度一致。其中，杆单元法典型节点最大水平位移出现在H2，为-2.85cm；等效加筋法中典型节点最大水平位移也是H2，为-3.08cm。

图8 加载后的位移矢量图

图8绘制了加载后袋内土体的位移矢量图，土工袋受竖向荷载和水平力作用，上层土工袋受力端首先受到挤压，局部产生滑动。随着水平剪力的增大，袋体其余部位沿受力方向逐渐发生滑动。加载过程中，上层土工袋由于受到竖向荷载、水平剪力和层间摩擦力作用，袋内土体发生侧向压缩和平动，袋内土体的位移从上到下逐渐减小。由于Abaqus中在模型顶部施加的刚性板约束袋子的滚动，导致矢量图中上层土工袋右侧并没有出现向上的鼓起，且从左到右逐渐减小。

4 结论

本文通过有限元数值模拟对土工袋无侧限压缩试验和剪切试验进行分析，结果表明：

（1）用杆单元法和等效加筋法模拟土工袋，计算结果合理并基本一致。使用杆单元法时，仅受张拉的杆单元对袋内土体起到约束作用，限制其位移，因此计算结果略小于等效加筋法。

（2）杆单元法中计算出的土工袋袋子张力充分阐明了土工袋的作用机理，通过与等效加筋法进行对比计算分析，也表明杆单元法的计算结果要更为理想。