卡尔曼滤波在车辆振动信号处理的应用研究*
严守靖,詹 伟,迟凤霞,王洋洋,奚晨晨
(浙江省交通运输科学研究院道路工程研究所,浙江 杭州 310023)
引言
近年来,利用车辆在沥青路面上行驶的振动信号,通过解析振动信号的频谱反演沥青路面行车舒适性、平整度等指标,对城市智能交通的管理和控制具有重要作用。沥青路面振动数据在采集过程中,振动信号掺杂着大量的噪声信号,需要进行数据的滤波降噪处理[1-4]。
随着概率论以及有关数据处理技术的发展,滤波降噪技术从声音、图像处理领域,逐渐迈向随机振动[5-8]等领域的应用。西安石油大学的高怡[9]为减少有色噪声的影响,提出了一种二阶自回归有色噪声抗差的卡尔曼自适应算法。哈尔滨工程大学的陈立伟[10]为解决局部立体匹配算法存在深度图边界区域不连续问题,基于图像边缘局部特征,对图像的像素点基于颜色阈值和边界条件构建自适应十字交叉区域,并对自适应窗口进行引导滤波代价聚合,提出了一种基于边缘约束的自适应引导滤波立体匹配算法。浙江工业大学[11]的周晓提出了一种基于卡尔曼滤波理论的预测模型,利用路段上下游的车辆平均速度预测未来时刻该路段的平均速度。卡尔曼滤波技术在其它领域的应用已经有了较为成熟的理论和方法,但对于车辆在沥青路面上行驶的振动信号处理,相关合适的滤波算法研究较少。
为探索卡尔曼滤波降噪技术在沥青路面振动信号处理过程中的可行性,实验对比分析了传统的平滑滤波和小波滤波降噪技术的处理方式,通过功率谱分析各自的降噪处理效果。以此评价卡尔曼滤波技术沥青路面振动信号处理的应用效果。
1 沥青路面振动信号数据采集
1.1 系统架构搭建
将移动终端固定在车辆上,选择某个移动终端提供流量,移动工作站和另外的移动终端通过主机的IP地址或者分布式业务网络(Distributed Service Network,DSN)来传输数据[12-15],如图1所示。通过上述设备即可搭建小型的局域网,完成移动工作站采集车辆运动状态信息数据的传输工作。经检测,该局域网具有较高的传输稳定性,在高大建筑物、恶劣天气环境下依然能完成数据传输工作。

图1 数据传输及整体架构
1.2 数据采集
该移动工作站的硬件电子设备通过MIL-STD-810G的测试,测试内容包含承重、高温、低温、振动等测试项目,本项目所用工作站能承受136kg的压力,能在-29℃-60℃的高温环境中进行持续工作。依靠移动工作站良好的工作性能,本项目开发了一套基于移动终端的车辆运动状态信息采集软件,能将智能手机上传感器能采集车辆的运动状态信息实时显示到移动工作站上,并将采集的数据及时保存到本地设备中,如图2所示。

图2 移动工作站采集车辆运动状态信息
2 滤波模型
2.1 数据预处理
在加速度信号数据采集的过程中,由于放大器随温度变化产生零点漂移、传感器频率范围外低频信号的干扰[16],加速度数据会偏离基线,而且偏离程度会随时间变化。为消除数据偏离度对信号的影响,本文首先采用最小二乘法进行数据处理[17]。
假设实际采集的加速度数据为[xk](k=1,2,3,...,n),数据采样频率为f,则采样的间隔为,则可采用m阶多项式来拟合,如式(2-1)所示。

aj(j=0,1,2,...,m)为拟合函数xˆk的待定系数,则实际加速度[xk]与拟合加速度函数xˆk的误差为 e,如式(2-2)所示。

过对待定系数求导数,如式(2-3)和式(2-4)所示。

通过对方程组的求解,可计算出m+1个线性方程的待定系数,即可得到拟合函数xˆk,则拟合加速度计算公式,如式(2-5)所示。

2.2 Kalman滤波
车辆在路面行驶过程中,智能手机主要放置在车辆仪表盘右侧前置面板上,其噪声主要来源于外部环境产生的低频噪声,采集过程中电子仪器设备产生的白噪声,车辆自身引擎激励产生的高频噪声。这些噪声都是非平稳的随机信号[18-20]。而路面给车辆激励产生的信号大多属于平稳随机信号,可视为平稳随机过程。而Kalman滤波器能根据前一时刻产生的估计值,再结合系统自身的状态转移方程算出新的状态估计值。这个方法既适用于平稳随机过程,也适用于非平稳随机过程[21-22]。
车辆在路面行驶过程中,假设系统的预测状态方程和观测状态,方程分别为式(2-6)和式(2-7)。

式中:xk-k时刻的真实值;xk-1-(k-1)时刻的真实值;uk-系统输入向量;wk-均值为0,zk-k时刻的观测值;vk-均值为0,协方差矩阵为R,且服从正态分布的测量噪声;A,B,H-分别为状态转移矩阵。
真实值与预测值之间误差,真实值与估计值之间的误差,可分别表示为式(2-8)和式(2-9),则k时刻的先验状态预测值与预测误差协方差可表达式(2-10)和式(2-11)。


令Q=E[wkwk)T],卡尔曼估计误差协方差矩阵为:

将式(2-12)代入式(2-11),故预测误差协方差为:

在卡尔曼滤波校正阶段,滤波器利用对当前状态的观测值修正在预测阶段获得的预测值,以获得一个更接进真实值的新估计值。其中观测误差为观测值zk与预测值之间的差异,如式(2-14)所示。

故卡尔曼估计值可表示为式(2-15)。

则卡尔曼估计误差协方差矩阵变化为式(2-16)所示。

令R=E[vkvkT],则卡尔曼估计误差协方差矩阵可表示为式(2-17)。

卡尔曼滤波本质是最小均方差估计,而均方差是Pk的迹,将式(2-17)展开并求迹。
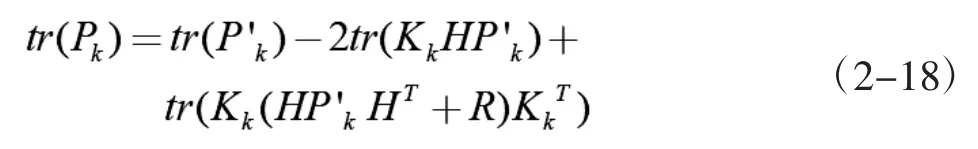
对式(2-18)中,通过迹对增益矩阵求导,使得 tr(Pk)最小,如式(2-19)所示。

最终得到卡尔曼滤波的增益矩阵Kk。

式中:R-测量噪声协方差;Kk-滤波增益矩阵;I-单位矩阵。
3 滤波降噪测试实验

图3 平滑滤波降噪

图4 小波滤波降噪

图5 Kalman滤波降噪效果

图6 信号降噪结果比较
实验测试了两种传统的滤波降噪方法,分别是平滑滤波降噪方法和小波滤波降噪方法。通过对竖向振动加速度信号的滤波测试,测试结果分别如图3和图4所示。
由图3和图4可以发现,平滑滤波和小波降噪滤波对原信号的削减较大,滤波后信号曲线变得较为光滑,但该现象也表明有效信号也被削弱。因此,传统的滤波方法在竖向振动加速度信号的处理,在噪声抑制方面较好,但有效信号的损失较大。
图5是Kalman滤波前后的沥青路面车辆行驶竖向振动加速度滤波结果,由该图可以看出,原始信号的特征保留比较清晰,针刺状信号明显减少。由此表明Kalman滤波降噪,不仅保留原始信号的有效数据,同时也抑制了大量的噪声信号。
4 结果分析
经过图3至图5的处理,已经可以定性地分析,不同降噪方法对沥青路面振动信号的处理效果。为进一步定量分析Kalman滤波方法的可行性和滤波降解效果,实验还分析了沥青路面振动信号在滤波前后的功率谱,如图6所示。
由图6可以看出,沥青路面振动信号在滤波降噪前,功率谱分布比较乱,沥青路面振动信号主频率间于1-1.5,有较多的噪声干扰。经过平滑滤波降噪后,高频的噪声信号几乎都被抑制,但同时沥青路面振动信号的有效信号也被抑制,几乎无法看出车辆的主频振动信号。相对于平滑滤波降噪,小波降噪无法抑制和消除低频信号的存在,同时沥青路面振动信号的功率谱间于0.5-1,显然与沥青路面振动信号的主频率不一致。而Kalman滤波既能消除高频的干扰噪声,也能保留沥青路面振动的有效信号。因此,针对沥青路面振动信号,Kalman滤波是较为合适的一种降噪方法。
5 结论
通过开展沥青路面振动信号的滤波降噪实验,比较分析不同滤波方法的处理结果,获得了以下的结论:
(1)针对沥青路面振动信号,平滑滤波的降噪效果最好,但容易削弱有效信号的强度,原始信号的主频率难以保存。
(2)相对于平滑滤波方法,小波滤波保留原始信号的主频率,但主频率发生移动,降噪后原信号的特征几乎都被消除,降噪效果不佳。
(3)卡尔曼滤波方法不仅能保存原始信号的特征,而且降噪后原信号的主频率依然清晰可见,高频噪声都被抑制。因此,卡尔曼滤波方法在沥青路面振动信号的处理过程中,具有良好的可行性与可靠性。

