发动机外部管路系统的卡箍布局多目标优化

徐培原，刘 伟

（1.航空工业航宇救生装备有限公司，湖北襄阳441003；2.西北工业大学力学与土木建筑学院，西安710129）

0 引言

管路系统是航空发动机介质传输和动力传递的通道，布局走向复杂。卡箍是固定与支承管路的重要装置，对提高管路刚度、实现管路频率调节具有重要作用，合理的卡箍布局是抑制管路系统振动的最有效、最简便的方法。目前，在工程中很多卡箍的选型、位置和数量是从原型机上直接比对移植过来的；一些局部管路的卡箍有时还需要技术人员现场调整，随机性较大，缺乏具体的理论指导，卡箍布置的经验性与随意性可能会导致管路结构的固有频率落入发动机工作频率附近，从而引发共振或局部振动应力过大。因此，研究发动机复杂管路的卡箍布局优化设计方案具有重要意义。

管路系统的卡箍位置优化已经引起了一些学者的关注。顾文彬[1]研究了直管在不同激励形式下的卡箍位置优化问题，表明自由振动、瞬态响应和随机响应下的卡箍位置具有不同的最优解；Wang[2]采用启发式优化算法，以减小形变和增大基频为目标，对直梁和支撑板结构进行卡箍位置优化；刘伟等[3]对多卡箍管路进行动力灵敏度分析，找出对目标影响较大的若干个卡箍位置参数，分别进行1 阶频率调节和降低随机振动应力的卡箍位置优化；智友海等[4]基于疲劳累积损伤的破坏准则方法，研究了随机振动下管路系统卡箍的位置对管路结构可靠性造成的影响；陈艳秋等[5]基于有限元法以频率调节和调幅为目标，对发动机导管卡箍刚度进行优化；李鑫等[6]将管路-卡箍系统的激励振源频率点的特征阻抗加权和最小设置为评价指标。目前卡箍优化研究存在2 个问题：（1）研究对象主要为直管或者平面管路，然而在实际工程中管路结构多样，走向复杂。而且，发动机管路和卡箍需要布置在机匣曲面上，需要研究曲面复杂管路的参数化方法；（2）现有优化的频率调节目标主要是单频段，然而发动机激励经常是1 个较宽的频段，结构的多阶固有频率都可能与激励频率接近，易引发管路其他频段的共振，诸如频率调节或者随机振动的单一目标的控制方法难以满足需求。因此，需要探讨发动机复杂管路卡箍布局优化的多目标优化方法。

本文采用灵敏度分析的方法确定了对发动机曲面上管路系统动力学特性影响较大的若干卡箍位置参数，以前4 阶固有频率远离发动机工作频率和随机振动应力均方根响应最小化这2 个原则为优化目标，对关键卡箍位置参数进行优化设计，以期为复杂管路的振动控制提供参考。

1 优化设计

对发动机外部管路卡箍布局进行优化设计，首先需要确定优化目标，本文的优化目标有2 个：（1）实现频率调节，使结构前4 阶固有频率远离外界激励；（2）随机振动的应力均方根响应最小化。

1.1 频率调节

根据振动设计要求，卡箍的安装应当使得结构的固有频率远离共振区（即发动机工作频率附近）。

令频率比λ=ω/ωn，ω为发动机工作频率，ωn为结构的第n阶固有频率，工程中通常取0.75＜λ＜1.25的区间为共振区[7]，由此可以近似推导出，当结构的第n阶固有频率满足0.8ω＜ωn＜1.3ω时，结构有发生共振的风险。为了使第n阶固有频率离开共振区，该阶固有频率Pn需要满足

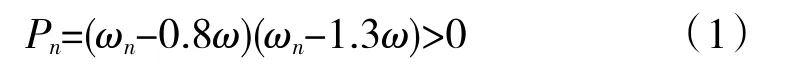
同时，为了比较不同的卡箍布局下第n阶固有频率远离共振区的程度，令Qn=|ωn-1.05ω|，Qn即为第n阶固有频率相对于共振区中心的偏离程度，优化的过程是在满足式（1）的同时尽可能使Qn最大化。

1.2 应力均方根响应

发动机管路处在复杂的振动环境中，需考察管路的随机振动响应。

随机振动可视为概率统计问题，无法获得某一瞬时具体响应数值，随机振动的响应分布可近似看作高斯分布，主要考察各物理量的均方根响应，某个物理量的均方根响应可看作该物理量响应分布的标准差。取管路结构x方向的最大应力均方根响应RS1为优化对象，在优化中尽可能减小RS1的数值[8]。

2 遗传算法

遗传算法是目前在工程领域中极为常用的1 种优化算法，是受自然界生物进化过程的启发而产生的。基于生物进化原则，根据每代种群个体对环境的适应程度来对个体进行筛选，适应度高的个体将被保留，适应度低的个体将被舍弃，之后被保留的个体再经历交叉、变异2 个步骤的处理，将其遗传信息传递给下一代。在逐代的遗传过程中，个体对环境的适应程度越来越高，越来越逼近最优解。遗传算法的主要流程如图1 所示。

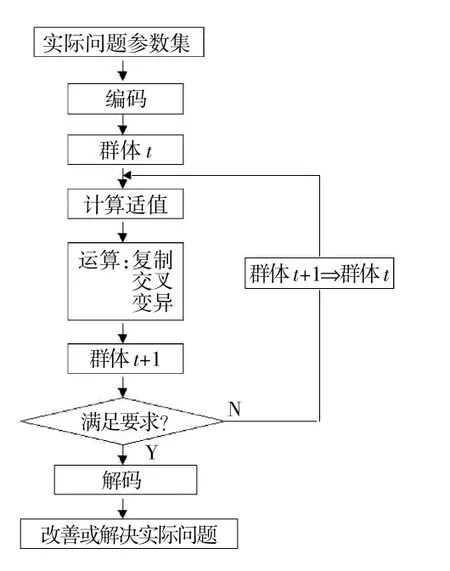
图1 遗传算法主要流程

在工程实际中多为多目标优化问题，本文选用的NSGA-II[9～11]算法是1 种较为常见的多目标遗传算法。

3 复杂管路系统的建模

3.1 卡箍模型

由于卡箍在整个管路系统中所占的质量分数与体积分数较小，在分析计算时忽略卡箍的质量与体积对管路系统带来的影响，重点研究卡箍对调整管路系统刚度的作用。

在工程中使用的卡箍虽然种类繁多，但作用基本相似，主要是限制管路径向位移。将卡箍简化为弹簧单元，一端连接管路，与发动机连接的另一端全约束，对沿管路径向的位移进行限制，如图2 所示。

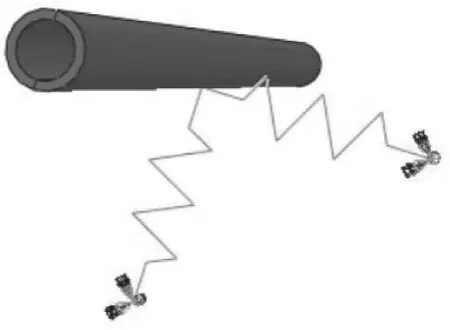
图2 卡箍限制管路的2 个径向位移

3.2 管路模型

发动机外部管路由直管、弯管、端口接头等组成，管路两端固定，其结构如图3 所示。与一般的直管优化不同，该结构的卡箍分布在圆柱曲面上，不仅需要考虑卡箍在直管上的直线移动，还需要考虑卡箍在弯管上的弯曲移动。

管路材料为1Cr18Ni9Ti 不锈钢，密度为7.8 g/cm3，弹性模量为206 GPa，泊松比为0.31，管径为8 mm，壁厚为1 mm，所受内压为21 MPa。

发动机管路结构主要由2 段长度不同的直管与1 段圆弧弯管组成（图3），L1为长直管，长2700 mm；L2为短直管，长1200 mm；L3为圆弧弯管，旋转半径为720 mm，旋转角度为240°。

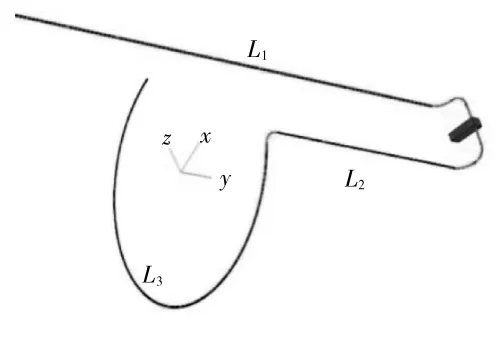
图3 发动机外部管路结构

3.3 原始卡箍位置分布

原始管路系统结构的卡箍分布如图4 所示。从图中可见，管路结构中有23 个卡箍，依次编号为K1～K23，L1上卡箍数量为9 个（K1～K9），L2上卡箍数量为4 个（K10～K13），如图4（a）所示；L3上卡箍数量为10个（K14～K23），如图4（b）所示。每个局部坐标系代表1个卡箍所在的位置，卡箍径向刚度为1×104N/mm。

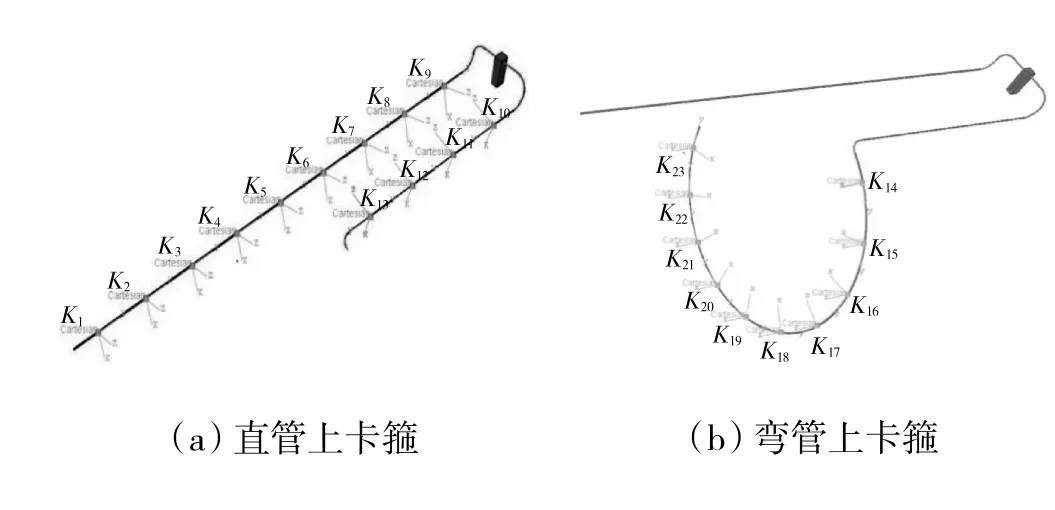
图4 在直管和弯管上卡箍的布局

3.4 原始管路结构的动态特性分析

在优化计算中，若设发动机在某一试车工况下的工作频率为100 Hz，根据式（1），对应的共振频段为[80 Hz，130 Hz]。结构受到的随机振动功率谱密度见表1。功率谱采用标准中规定的机载设备谱，激励沿如图3 所示坐标系中的x方向加载在结构整体上。

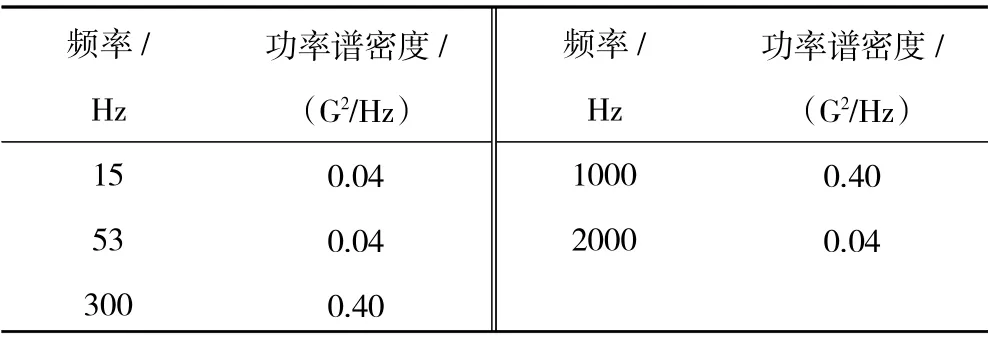
表1 结构受到的随机振动功率谱密度

对原管路结构进行模态分析与随机振动分析，前4 阶固有频率与x方向最大应力均方根见表2。

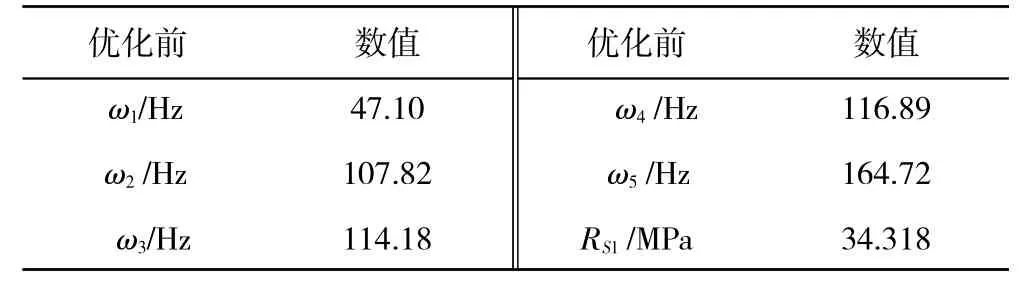
表2 原管路系统优化前4 阶固有频率和应力均方根计算结果

从表2 中可见，结构在优化前x方向最大应力均方根响应为34.318 MPa，且第2、3、4 阶固有频率均处于共振区[80 Hz，130 Hz]之内，有引发共振的风险，需要对卡箍位置进行优化。

4 卡箍位置的参数化与灵敏度分析

4.1 卡箍的参数化建模

参数化设计可以修改原有的模型以使其达到新的目标状态，便于在不同的设计参数下对结构进行分析。在所研究的管路系统中，卡箍数量众多，分布方式复杂，选取卡箍模型的安装位置作为参考变量，可以随时调整卡箍的位置参数，从而通过仿真计算评估不同的卡箍布局对于管路系统刚度的影响，对管路系统的动态响应特性做出预测，对多卡箍复杂管路系统的卡箍安装提供指导。

4.2 卡箍位置的参数化

为了对结构进行优化设计，首先需要将卡箍位置参数化，如图5（a）所示。对于L1上的卡箍K1～K9，设L1左端约束处为参考零点，卡箍Ki到L1参考零点的距离为mi（i=1，2，…，9）；对于L2上的卡箍K10～K13，设L2右端起始处为参考零点，卡箍Ki到L2参考零点的距 离 为mi（i=10，11，12，13）；对 于L3上 的 卡 箍K14～K23，设L3与接头连接处为参考零点，参考零点绕圆弧管路圆心旋转到达卡箍Ki位置时所转动的角度为θi，为了便于卡箍编号与位置参数对应，参数θi由i=14 开始计数（i=14，15，…，23），如图5（b）所示。mi与θi即为表达卡箍位置的参数，当全部参数确定时，管路上有惟一1 种卡箍布局与之对应。

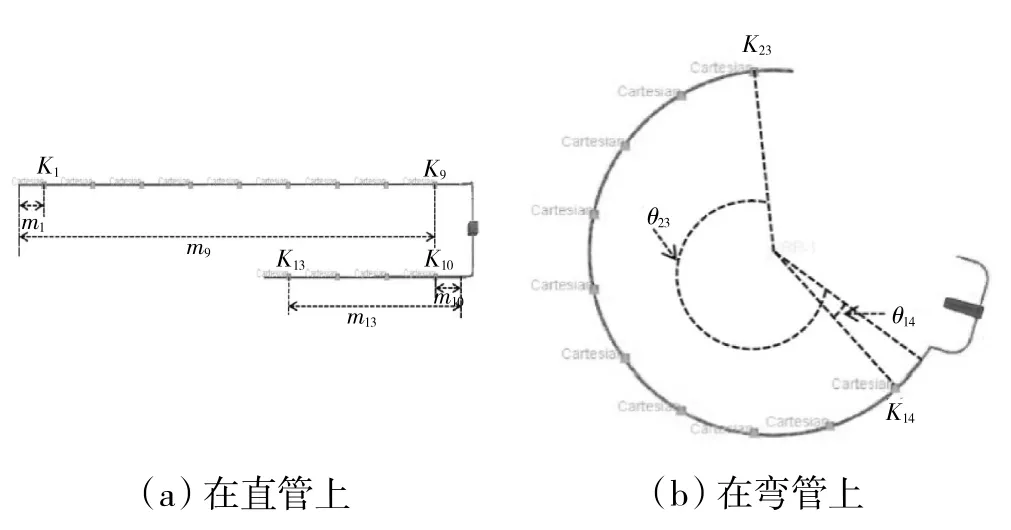
图5 在直管和弯管上卡箍位置的参数化

4.3 卡箍位置参数灵敏度分析

设函数y=f（x），x为设计参数，当x=x0时增加Δx，设计响应变化为Δy，用来表述在x0附近x对y的敏感程度，往往设计响应同时与几个设计参数有关，故用响应对该参数的偏导数来表述设计参数对设计响应的敏感程度。

由于发动机管路卡箍数量众多，对所有卡箍进行位置优化是复杂且效率极低的工作，需要选择对优化目标影响较大的卡箍来分析，因此在优化前需要对参数进行灵敏度分析，挑选灵敏度较大的参数来进行控制与优化，关于灵敏度的求解问题，文献[3]中有详细说明。

求解各参数对前4 阶固有频率以及x方向应力均方根的灵敏度，由于mi与θi的单位不同，为了对其灵敏度进行比较，依据归一化公式（2）进一步求解各参数的归一化灵敏度归一化灵敏度表达函数相对增量与参数相对增量之比称为相对灵敏度

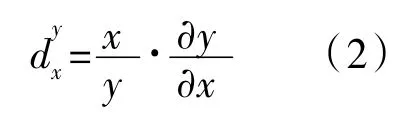
相对灵敏度计算结果如图6 所示。从图中可见，挑选对前4 阶固有频率和应力均方根响应影响最大的卡箍位置参数，对第1～4 阶固有频率影响最大的参数分别为θ14、m13、m9、m10，对应力均方根响应影响最大的参数为θ21，着重对这5 个变量进行优化设计。

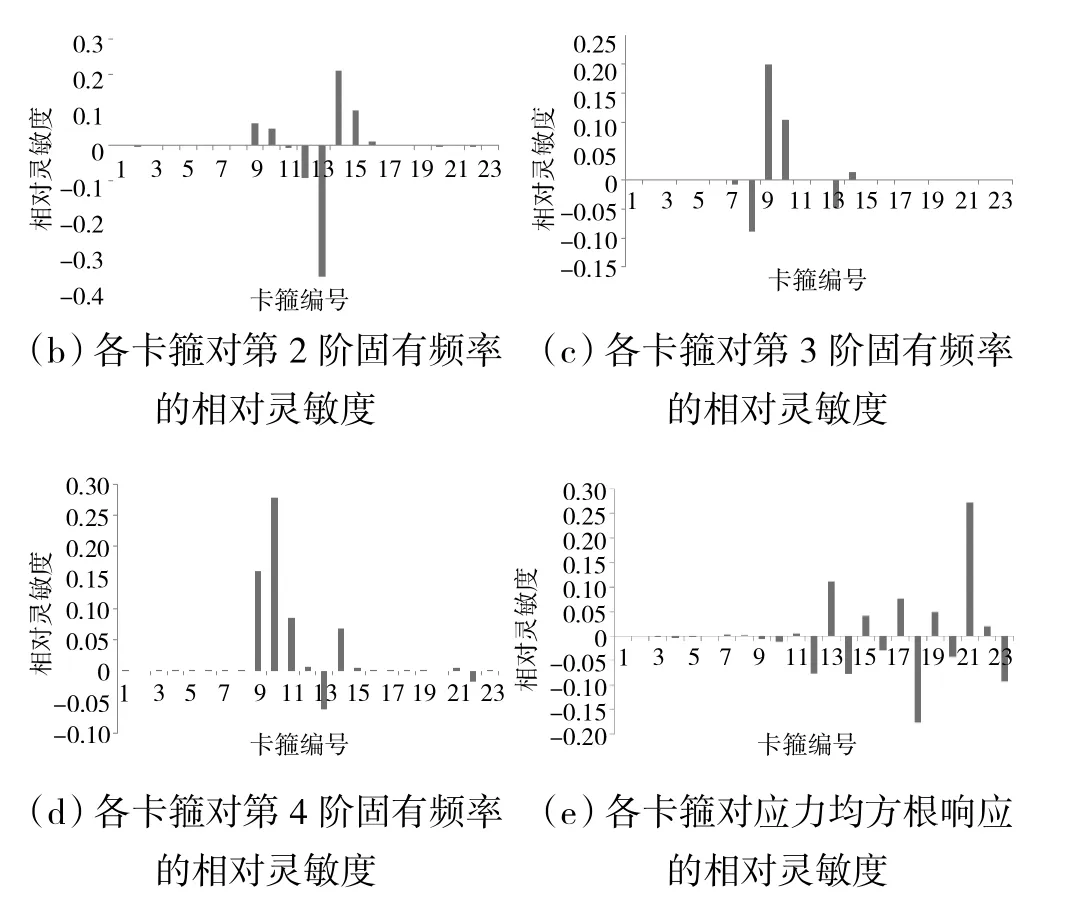
图6 卡箍对各参数的相对灵敏度分析

5 NSGA-II 算法下卡箍布局的适应度评估

卡箍布局的适应度由优化的目标函数决定，根据指定的2 个优化目标，优化设计所设定的目标函数为

5.1 Pareto 非支配解集

为了对卡箍布局的适应度进行评估，首先对Pareto 非支配解集的概念进行说明。

对于最小化多目标问题，n为任意正整数。

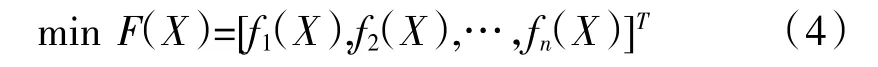
为目标向量函数给定1 个变量

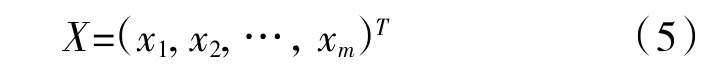
设该变量的约束条件为

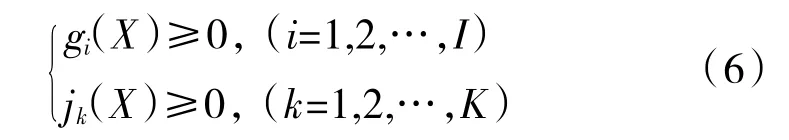
根据多目标优化问题的数学表达方式来看，最终要求的解是1 个设计变量组合，在满足约束条件的前提下，使优化目标达到最优，但是由于在多目标优化问题中，目标函数之间可能会有相互竞争的关系，所以最终只能得出相对较优的方案。优化得到的不是1个最优解，而是一系列相对最优解组成的解集，称为Pareto 最优解集或Pareto 非支配解集。

对于2 个向量Xu和Xv，当且仅当对于任意正整数w

有

且至少存在1 个正整数e

使得

则称Xu支配Xv。

对于2 个向量Xu和Xv，当且仅当对于

使得

同时

使得

则称Xu与Xv互不支配[12-13]。

非支配解集概念的提出，为多目标遗传算法的个体优劣评估提供了重要途径，解决了多目标遗传算法中适应度函数难以构建的问题，也为卡箍不同的优化方案的优劣提供判断依据。

5.2 适应度评估

在单目标遗传算法中，基因信息被遗传至子代个体的概率主要由适应度函数决定，然而在多目标优化中，适应度函数的构建比较困难，无法适当地评估每个优化目标，因此NSGA-II 定义了1 种比较运算符，用来对种群中的某2 个随机选择的个体进行优劣评估，该运算符与以下2 个参数相关。

（1）无支配前沿分类。

NSGA-II 对整个种群进行排序，以种群中每个个体的无支配程度为评价标准，将拥有相同的无支配性的个体集合在一起成为1 个无支配前沿，从而将种群划分为多个无支配前沿。

以约束条件式（3）为例，开始时将种群的第1 个卡箍布局解x1放入空集Y中，之后的每个卡箍布局xi都与Y中的每个解进行比较，若xi支配Y中的某一解，则将那个解从Y中移除；若xi被Y中的解支配，则忽略xi；若xi不被Y中的任何1 个解支配，则将xi留在Y中。当种群中所有卡箍布局都进行了比较之后，留在Y中的解即为非支配序号为1 的个体。将序号为1 的解移出种群，继续上述操作，直到所有卡箍布局都获得序号，这个序号可以用来初步辨别种群中个体的优劣程度。

（2）密度估计值。

在无支配性排序之后为了让个体之间的优劣得到进一步区分，NSGA-II 采用的方法是计算出指定的某个个体相邻的2 个个体目标函数之间的距离，用来判别种群在选定的个体位置附近的密集程度，也称为拥挤度。在指定个体附近种群的分布越稀疏，则对于种群的多样性越有利，该方法称为密度估计法（如图7 所示），在搜索过程中可兼顾种群的多样性。

图7 密度估计值

卡箍布局解i的密度估计值为

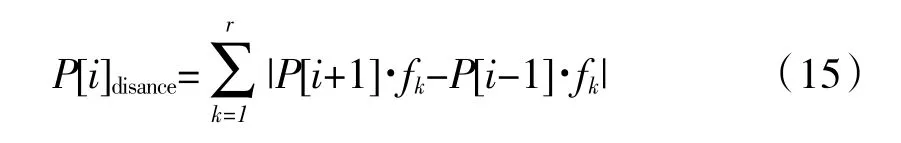
式中：P[i+1]·fk为第i+1 个卡箍布局解对应的第k个目标函数值。

每个卡箍布局对应的最终适应度可以由上述2种方法得到的数值相结合而得出，评价准则为：（1）在2 个解处于不同的无支配前沿的情况下，认为无支配程度序号低的卡箍布局解适应度更高；（2）在2 个解处于同一无支配前沿的情况下，认为密度估计值较大的卡箍布局解适应度更高。

6 基于NSGA-II 算法的卡箍布局优化流程

6.1 编码

遗传算法首先需要编码，其意义是将优化问题中的变量参数化，即将卡箍的布局转化为遗传算法所能搜索的参数形式，飞机液压管路系统的优化设计变量卡箍布局的变化具有连续性，所以液压管路系统卡箍的优化设计采用浮点数编码方式，卡箍的位置由矩阵来表示，矩阵第1 行表示卡箍的编号，由1～n，之后的几行分别表示各卡箍需要优化的参数。本次优化只考虑卡箍的布局，所以只对卡箍的布局进行编码。卡箍的布局用向量L={l1，l2，l3，…，ln}来表述，则卡箍在优化中的编码为

6.2 初始种群生成

进化操作的第1 步是要生成1 个由若干初始解组成的初始种群，在工程中面对的优化问题大多是拥有复杂结构和多参数的，一般很难对解空间拥有先验知识，所以初始种群中的个体以随机方式产生，种群内的个体数需要在计算前设置，设每代的个体数为D，设置D=12。

6.3 适应度评估与选择

依据第5.2 节对所有初始解进行无支配前沿分类和密度估计值计算。根据求得的非支配序号和密度估计值对解进行筛选，其准则为：（1）在2 个卡箍布局解处于不同的无支配前沿的情况下，选择无支配序号低的解；（2）在2 个卡箍布局解处于同一无支配前沿的情况下，选择密度估计值较大的解。被选择的解会被放入“交配池”。

6.4 交叉操作

NSGA-Ⅱ算法每次从“交配池”中随机选择2 个个体，对应不同的2 种卡箍布局S1和S2，采用交叉算子，产生2 个新的子代S1’和S2’。对于第i个变量，其交叉过程如下：

（1）随机产生1 个数字uc，i∈[0，1]。

（2）通过多项式概率分布计算参数ξi，控制父子2代相接近的概率

式中：非负参数ηc为交叉分布指数，ηc的大小表示子代与父代之间的距离，参数越大表明二者越接近，参数越小表明二者越疏远。

（3）交叉产生子代的计算式为

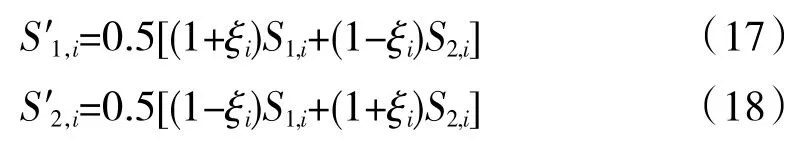
6.5 变异操作

NSGA-Ⅱ算法会在某个卡箍布局解S1的临近位置产生变异后的布局解S2。对于第i个变量其变异的过程如下：

（1）随机产生1 个数字um，i∈[0，1]。

（2）计算参数δi

（3）变异子代的计算式为

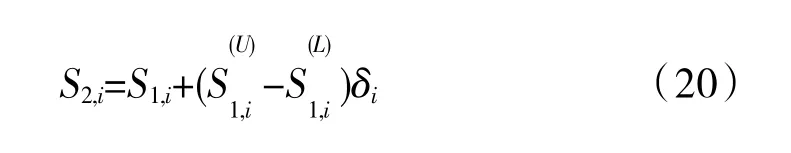
6.6 循环

在经过选择、交叉、变异的操作之后，形成新一代的12 个卡箍布局解重新进行适应度评估，循环计算直至达到设定的计算代数，本文设置的代数为20。

7 卡箍位置优化设计

根据灵敏度计算结果，选择出需要进行优化的5 个卡箍位置参数，其取值范围见表3。

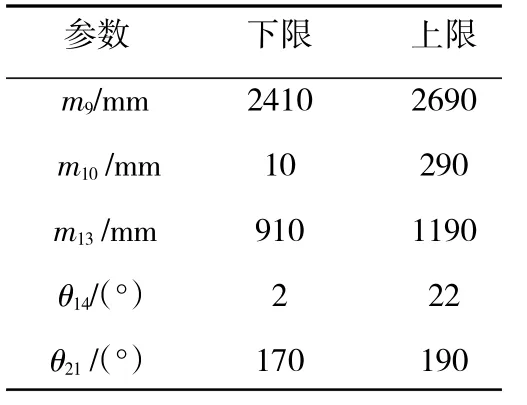
表3 参数取值范围

优化要求前4 阶固有频率最大限度远离共振区[80 Hz，130 Hz]，并使随机激励下的应力均方根最大值尽可能减小。

采用多目标遗传算法进行优化计算，设置遗传代数Q=20，每代的种群数D=12，交叉分布指数ηc=10，变异分布指数ηm=20，优化计算主要流程如图8 所示[14-15]。

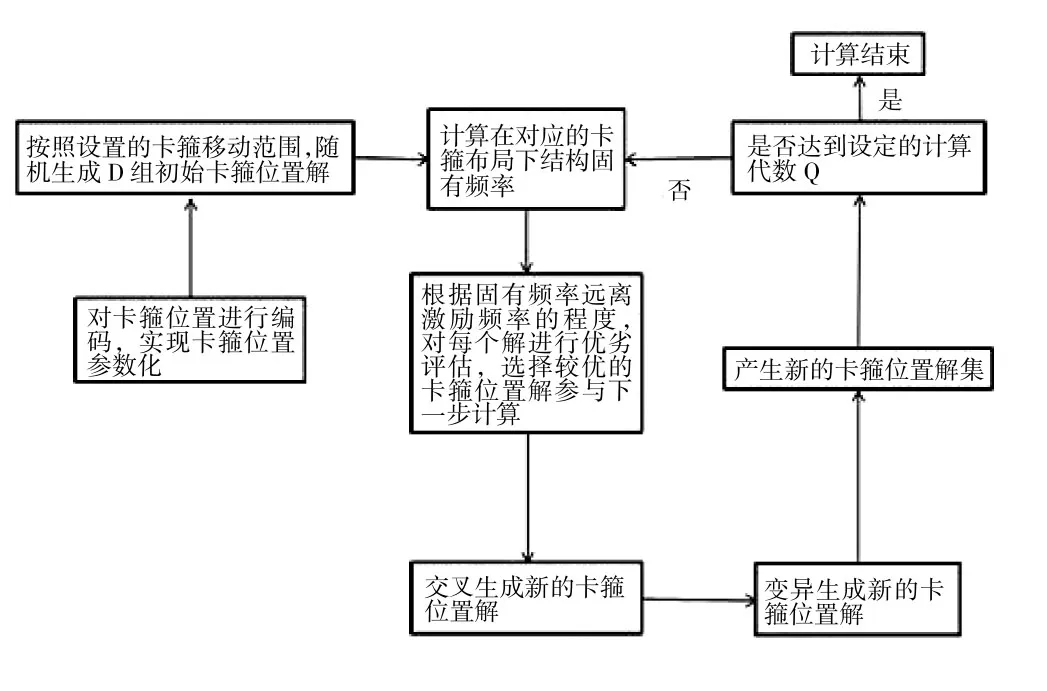
图8 优化计算主要流程

计算结束后，从最后一代的12 个卡箍布局解中挑选出所有无支配序号为1 的解，并从中选择密度估计值最大的3 个结果，3 种优化方案与优化前结构固有频率对比如图9所示，优化结果见表4。

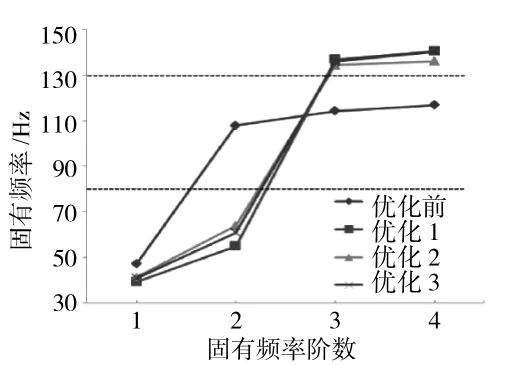
图9 优化前、后结构固有频率对比

从图中可见，优化后的结构固有频率都离开了共振区[80 Hz，130 Hz]，实现了频率调节的目标，可以有效避免结构因发动机工作而引发共振，而且卡箍位置优化后，管路结构的x方向最大应力均方根响应与优化前的34.318 MPa 相比也有不同程度降低（至少降低17.3%）。

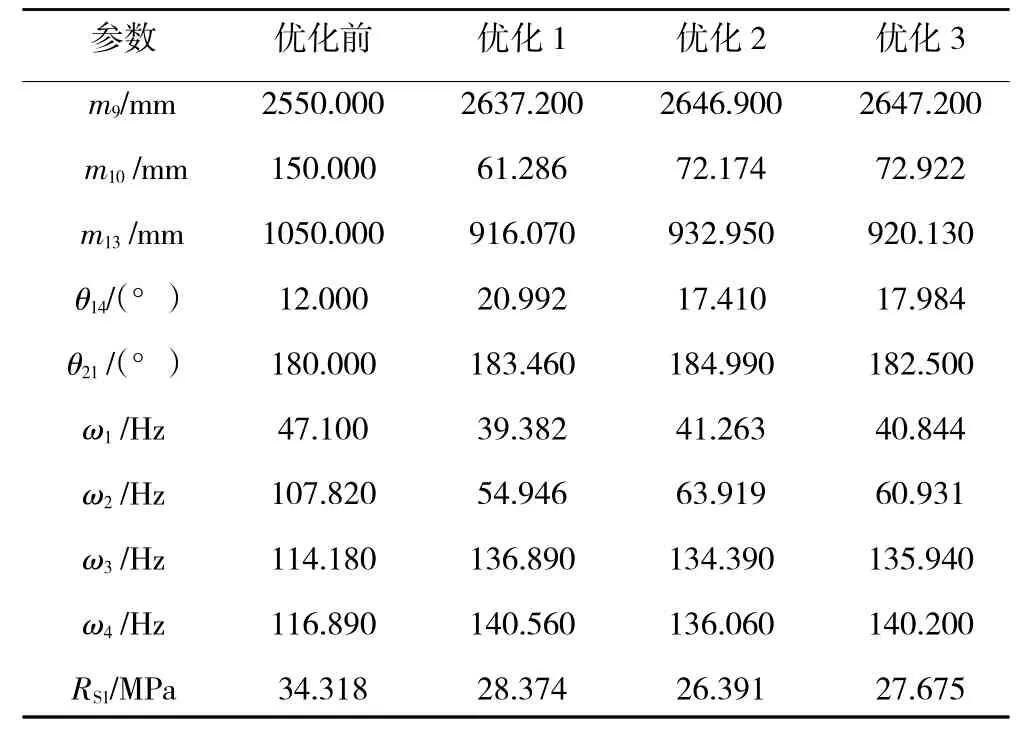
表4 优化结果

结合表4、图9 对3 种优化方案进行进一步对比分析，发现优化1 使得结构的固有频率最大限度地远离了共振区，但并没有最大限度地减小结构的x方向最大应力均方根；优化2 对应最小的应力均方根，但共振频段偏离程度不如其他2 个优化方案的，可能造成某个频率的谐响应劣于其他2 个优化方案的；优化3 的频率调节和减小最大应力均方根的效果介于二者之间。

8 结论

本文对发送机外部3 维复杂管路系统的卡箍布局进行了优化设计，得到如下结论：

（1）对于复杂管路多卡箍优化问题，某些卡箍对结构的动态特性拥有更显著的影响，在优化计算前进行灵敏度分析可以提高优化设计的效率。

（2）采用的多阶固有频率调节优化适用于任意频段的外界激励，可以保证多阶固有频率远离激励频段。

（3）引入转动角度作为参考变量，将传统的直管卡箍位置优化扩展到弯管上，实现了发动机曲面上的复杂管路系统的多卡箍位置优化。