基于干扰观测器的弹丸协调臂Terminal滑模控制

潘润超，李志刚，管佳伟

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

弹丸协调臂作为弹药装填系统中不可或缺的一部分，其主要任务是接收从弹仓中选定的弹丸，从固定的起始位置起，根据控制器结合当前射角计算出的理想轨迹，携带弹丸快速稳定地绕火炮耳轴回转至炮尾的正后方，为后续的输弹动作提供前提条件。弹丸协调臂作为机械、液压、控制互相耦合的非线性电液伺服系统，工作过程中表现为一种高速重载的机械臂，与一般的机械产品相比，具有参数变化范围大、存在剧烈冲击振动、工作环境复杂多变等特点，因此要实现在运动过程中保持较高的动态精度与到位精度极具挑战性。

传统电液伺服系统控制方法常为根据机械结构部分和液压部分推导出系统的状态方程，然后基于数学模型去设计滑模控制器。但这样很容易忽略掉电液伺服系统中存在的参数不确定、外界干扰等问题。而在普通的滑模控制中，通常选择一个线性的滑动超平，使系统达到滑动模态以后，跟踪误差渐进收敛为0，并且渐进收敛速度可以通过选择滑模面参数调节矩阵任意调节。但无论怎样，状态和跟踪误差都不会在有限时间内收敛为0，且因为滑模控制率中切换项的存在，抖振问题也无法避免。许多学者[1-8]做了实验和研究，有效地解决了上述问题。

1 问题描述与动力学模型

1.1 弹丸协调臂机械部分动力学建模

弹丸协调臂电液伺服系统模型如图1所示。火控系统根据所需协调角度设计运动轨迹，并将命令输入给上位机，结合传感器反馈的油缸两腔压力计算所需控制电压，控制伺服阀阀芯位移大小来调节运动快慢，使之达到理想的动态品质与稳态精度。弹丸协调器的工作原理为从接弹位将弹丸协调运动到与身管平行的输弹位。整个过程要求平稳，无冲击，到位误差控制在±3°以内，以保持较高的卡膛一致性，从而保证火炮弹药自动装填系统可靠性，提高火炮射速。

图1 弹丸协调臂电液伺服系统模型

图1模型中点A和点O为系统的2个固定支撑点，点B为油缸支撑弹丸协调臂运动支点，点C和点D分别为协调臂质心和弹丸质心。具体参数定义如下：l为固定支点A与运动支点B之间的距离；l1为油缸支撑弹丸协调臂运动支点B到固定支撑点O的距离；l2和l3分别为协调臂架体质心和弹丸质心到固定支撑点O的距离；l4为固定支撑点A和固定支撑点O之间的距离；α为点O与竖直方向的夹角；θ为协调器协调角度，变化范围为0～90°；β为油缸推杆与协调臂架体夹角；F为油缸推力；m1g为协调器架体所受重力；m2g为弹丸所受重力；p1为油缸无杆腔压力；p2为油缸有杆腔压力；ps和pr分别为供油压力和回油压力；u为控制器输出到伺服阀的电压信号。

弹丸协调臂运动方程可表示为

(1)

1.2 弹丸协调臂液压部分动力学建模

油缸两腔的流量方程可表示为

(2)

Q1和Q2分别为油缸无杆腔和有杆腔进油量或回油量；Cd为流量系数；阀芯位移xv=kvu，其中kv为伺服阀和放大器总增益，u为控制器输出控制电压；W为阀口面积梯度；ρ为液压油密度。且0≤pr≤p1≤ps，0≤pr≤p2≤ps；s(xv)为阀芯位移的函数，定义为

(3)

油缸两腔的连续性方程为

(4)

1.3 弹丸协调臂状态方程推导

油缸两腔压力平衡方程为

A1p1-A2p2=F

(5)

结合式(1)～式(5)可得

(6)

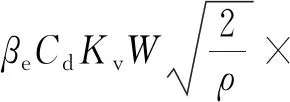
K1、K2、K3和ΔF均为非线性未知可变函数。

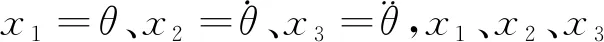
(7)

u为系统的输入；y为系统的输出；d表示系统参数不确定性与外部干扰的总和，且d有界，d≤D。定义未知参数集X=[x1x2x3]T。

2 指数收敛干扰观测器设计

2.1 指数收敛观测器设计

设计观测器的基本思想就是用估计输出与实际输出的差值对估计值进行修正。针对状态式(7)中存在外界干扰项的情况，设计估计误差导数为

(8)

(9)

定义辅助参数向量为

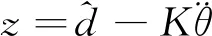
(10)

对式(10)求导得

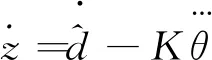
(11)

将式(9)代入式(11)得

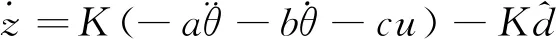
(12)

则干扰观测器可设计为

(13)

2.2 观测器收敛性证明

由式(13)可得

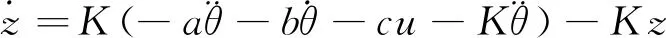
(14)

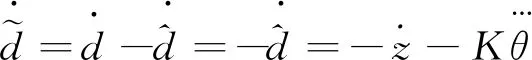
(15)

将式(10)和式(14)代入式(15)得

(16)

3 Terminal控制器设计与分析

3.1 控制器设计

针对系统状态方程式(7)，为了控制器设计方便，定义f(x)=ax3+bx2，g(x)=c。则式(7)可化简为

(17)

由系统状态方程可知，系统为三阶系统，n=3。设位置指令为xd，定义s0表达式为

(18)

定义一种具有递归结构的快速滑动模态表示为

(19)

由式(19)可得

(20)

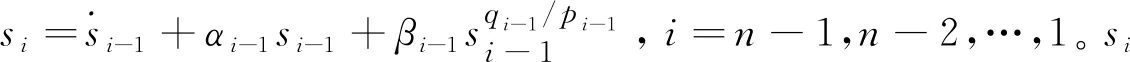
(21)

则可知当l=2时，有

(22)

将式(22)代入式(20)中，得

(23)

通过递推，可得

(24)

将式(17)和式(18)代入式(24)可得

(25)

设计控制律为

(26)

(27)

3.2 全局稳定性证明和收敛性分析

定义Lyapunov函数为

(28)

将式(16)和控制律式(27)代入式(28)得

(29)

图2 弹丸协调臂电液伺服控制系统结构

4 实验仿真与验证

4.1 弹丸协调臂运动轨迹设计

根据实际，系统在MATLAB/Simulink里建立弹丸协调臂仿真模型，并设计控制器。为了保证整个运动过程平稳，特别是在启停阶段没有过大的加速度突变过程，采用S型速度曲线规划算法，0～1 s内静止不动，1～2 s弹丸协调臂从0°运动到60°，规划轨迹如图3所示。

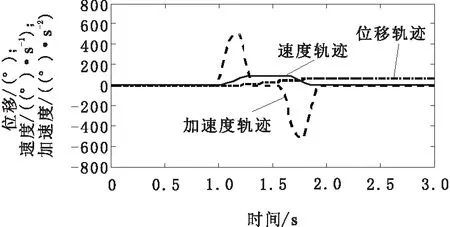
图3 协调臂的运动轨迹规划

整个过程让加速度处于连续变化的规程，没有加速度突变的情况，有利于控制量不会产生突变，减少了协调臂在运动过程中因为控制量突变而引起的抖动，保证了较好的运动动态品质。

4.2 仿真结果与分析

通过不断调试，最终获得的控制器参数为α0=10，β0=5，α1=80，β1=60，q0=9，p0=8,q1=7,p1=8，p=10，q=8，K=300,γ=30，φ=900。在仿真模型中所加外界干扰为d=120sin(πt)+60。伺服阀的允许输入电压范围为-10～+10 V，Terminal滑模控制器输出控制电压如图4所示。

从图4可看出，控制器输出连续，大小符合伺服阀输入大小要求，且曲线较为平滑，无明显抖动。位置、速度、加速度跟踪误差分别如图5、图6和图7所示。

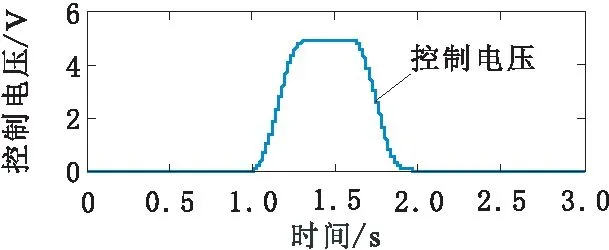
图4 控制电压

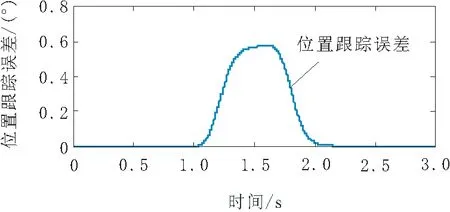
图5 位置跟踪误差

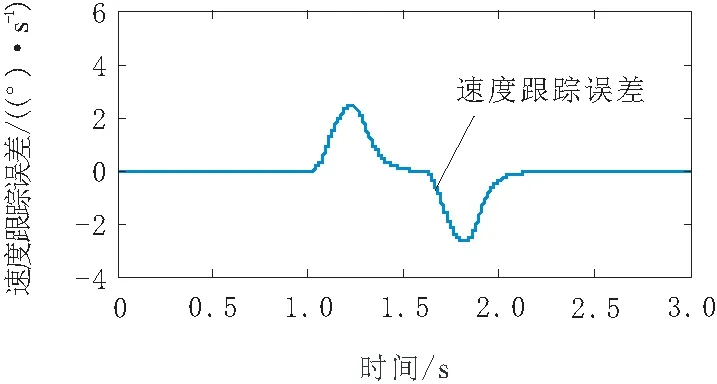
图6 速度跟踪误差

图7 加速度跟踪误差

由图5～图7可知，动态位置跟踪误差最大为0.575°，到位位置误差约为0.02°；动态速度跟踪最大误差为2.513 (°)/s；动态加速度跟踪最大误差为21.73 (°)/s2。整个运动过程平稳，速度和位置变化较稳定，无明显抖振，满足实际工况要求。干扰观测器扰动观测曲线如图8所示。

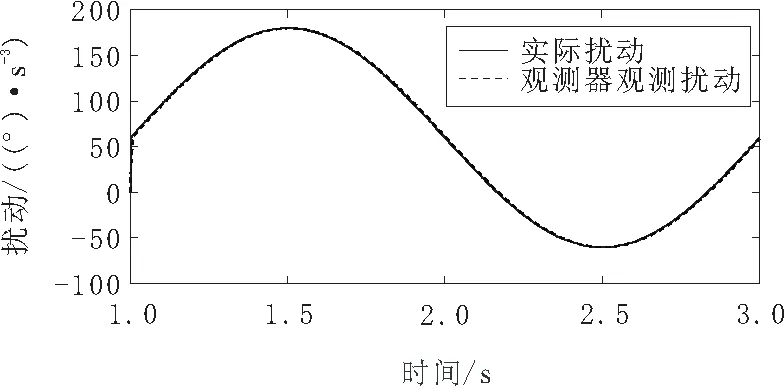
图8 观测扰动与实际扰动曲线

由图8可以看出，基于指数收敛观测器的观测精度较高且反应速度快，约需0.02 s就可以准确估计出扰动大小，收敛速度快，并且后续观测误差最大为1.256 (°)/s3，满足实际工况需求。

5 结束语

提出的基于干扰观测器的弹丸协调臂Terminal控制方法，在处理状态方程时，考虑到协调臂电液伺服系统存在参数不确定以及时变干扰问题，统一处理为外界干扰，利用基于指数收敛的观测器进行估计，并在控制律中进行补偿，提高了系统的鲁棒性。同时为了克服传统滑模控制在线性滑模面条件下，状态渐进收敛导致无法在有限时间内到达平衡状态的特点，设计了一种全局快速Terminal滑动模态，使系统状态在有限时间内迅速收敛到平衡状态。

仿真结果证明，所提出基于干扰观测器的弹丸协调臂Terminal控制方法能有效提高系统的鲁棒性，对参数不确定性以及时变干扰有较好的适应性，且能减弱抖振现象，保证弹丸协调臂在运动过程中有较好的动态精度和到位精度。