大跨径独塔斜拉桥几何非线性静力分析
文 新
(湖南省高速公路集团有限公司, 湖南 长沙 410015)
近年来,由于我国桥梁建设水平飞速发展,跨越高山峡谷与江河湖海的大桥越来越多,各类型桥梁也向着大跨径方向发展,斜拉桥以其强大的跨越能力成为桥梁设计中的一种常用桥型。独塔斜拉桥的跨径由于其结构组成而受到限制,大部分独塔斜拉桥均为中小跨径桥梁,设计大跨径独塔斜拉桥时其结构安全显得尤为重要。斜拉桥的几何非线性效应对结构内力影响较大[1],本文以某大跨径独塔斜拉桥为例,采用MIDAS/CIVIL建立该桥空间有限元模型,计算并分析了该桥考虑垂度效应、梁柱效应与大位移效应时主梁的内力响应特征,研究成果可为同类型桥梁内力计算提供一定参考。
1 斜拉桥几何非线性分析方法
1.1 垂度效应
斜拉索在自重作用下产生下挠的现象为垂度效应,且斜拉索越长其自重作用越明显。本文采用等效弹性模量法考虑垂度效应,利用Ernst公式对斜拉索的弹性模量进行修正[2],即在弹性伸长公式中计入垂度的影响,Ernst公式为:
(1)
式中:Eeq为考虑修正后的等效弹性模量,KPa;Ee为斜拉索钢材弹性模量,KPa;L为斜拉索水平投影长度,m;γ为斜拉索单位体积重力,kN/m3;σ为确定工况斜拉索应力,KPa。
在MIDAS/CIVIL中采用桁架单元模型斜拉索,并用Ernst公式对其弹性模量进行修正即可考虑垂度效应。
1.2 梁柱效应
在斜拉桥结构中,由于斜拉索的拉力作用,使得主梁与主塔承受了巨大的轴力而始终处于压弯状态,在二者变形过程中,弯矩与轴力相互影响,即为梁柱效应[3]。对于细长构件,梁柱效应影响尤为明显。
梁柱效应的静力分析方法为:将轴力作为参数计入杆单元刚度矩阵中,并引入稳定函数[4]对刚度矩阵进行修正。在MIDAS/CIVIL中只需在P-delta对话框中设置相应的荷载工况和迭代次数即可。
1.3 大位移效应
大位移是指结构在荷载作用下产生形变,导致荷载的作用位置与方向发生明显变化,进而影响结构切线刚度矩阵。此时,结构切线刚度由恒量变为以结构几何参数为自变量的函数,平衡方程也由线性关系变为非线性关系,叠加原理不再适用[5]。
本文采用更新的拉格朗日列式(U.L)求解大位移问题,其表达形式为:
[K0+Kσ]d{δ}=d{f}
(2)
在MIDAS/CIVIL非线性分析对话框中勾选几何非线性,程序将通过设置合适的载荷步逐级增加荷载,不断更新结构刚度矩阵,直至不平衡力足够小时计算终止。
2 工程概况
工程为湖南某跨河独塔斜拉桥,该桥结构形式为独塔双索面预应力混凝土箱梁斜拉桥,全桥采用刚构体系,边跨设有1个辅助墩。桥梁全长362m,主跨为198m,边跨为164m(102 m+62 m),主梁截面形式为单箱三室预应力混凝土箱梁,桥面全宽30.5m,梁高3.2m,混凝土标号为C55。主塔两侧各26对扣索,索面呈扇形布置,斜拉索采用φ7mm镀锌平行钢丝,标准强度为1770MPa,共计104根。扣索M1-M26及扣索S1-S16索间间距均为7m,扣索S17-S26索间间距为4.5m,所有扣索在主塔上的索距均为2.0m。该桥桥型布置与主梁横断面见图1、图2。

图1 独塔斜拉桥桥型布置图(单位: cm)
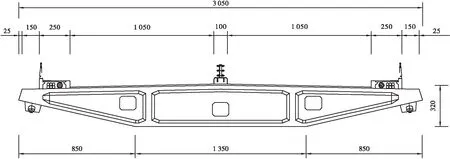
图2 主梁横断面图(单位:cm)
3 有限元模型的建立
该桥属于典型空间受力结构,采用MIDAS/CIVIL软件建立该桥空间有限元结构模型,主梁与主塔采用梁单元模拟,斜拉索采用只受拉桁架单元模拟,对于中小跨径的斜拉桥采用考虑Enrst公式修正的等效桁架单元可得到比较精确的计算结果[6]。全桥共672个节点,780个单元。主梁及桥面系采用脊梁模式[7]建立,主梁与主塔之间采用弹性连接中的刚性连接约束,索塔底部采用固结约束。主梁边支座与辅助墩均采用一般支承,约束Dy与Dz,该桥有限元模型见图3。

图3 独塔斜拉桥有限元模型示意图
4 几何非线性静力分析
4.1 成桥索力计算与非线性效应组合
采用最小弯曲能量法对合理成桥状态的索力值进行求解,具体步骤为先减小塔、梁的轴向刚度104~105倍[8],考虑自重、压重、二期恒载、预应力荷载,可直接求得桁架单元I端与J端内力,求和后取平均值,得到一组与合理成桥状态索力较接近的初索力,最后进行微调即可[9]。最终求得的索力值见表1。
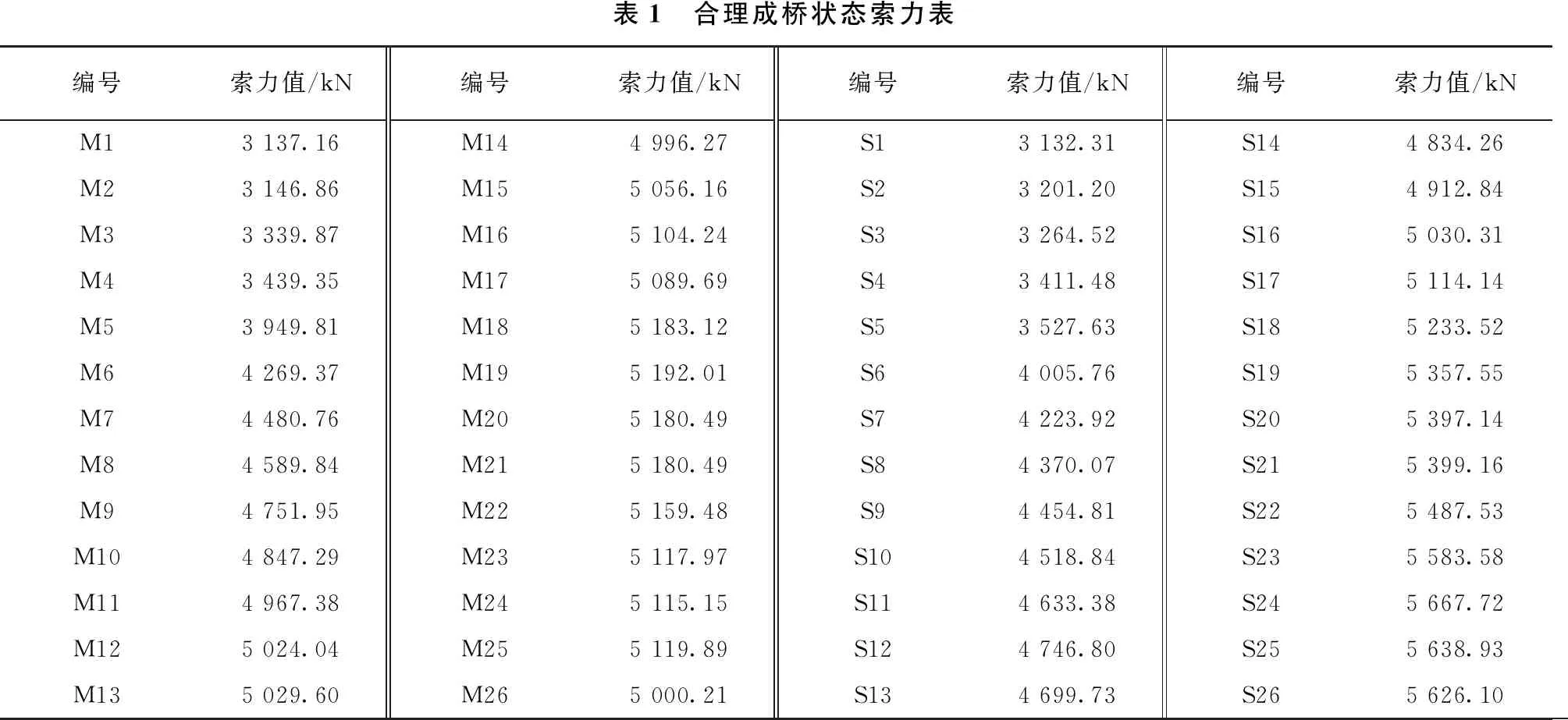
表1 合理成桥状态索力表编号索力值/kN编号索力值/kN编号索力值/kN编号索力值/kNM13 137.16 M144 996.27 S13 132.31 S144 834.26 M23 146.86 M155 056.16 S23 201.20 S154 912.84 M33 339.87 M165 104.24 S33 264.52 S165 030.31M43 439.35 M175 089.69 S43 411.48 S175 114.14 M53 949.81 M185 183.12 S53 527.63 S185 233.52 M64 269.37 M195 192.01 S64 005.76 S195 357.55 M74 480.76 M205 180.49 S74 223.92 S205 397.14 M84 589.84 M215 180.49 S84 370.07 S215 399.16 M94 751.95 M225 159.48 S94 454.81 S225 487.53 M104 847.29 M235 117.97 S104 518.84 S235 583.58 M114 967.38 M245 115.15 S114 633.38 S245 667.72 M125 024.04 M255 119.89 S124 746.80 S255 638.93 M135 029.60 M265 000.21 S134 699.73 S265 626.10
为探究几何非线性效应的影响,建立以下4种工况对该桥主梁空间力学响应进行对比分析。
工况1:仅进行线性分析。
工况2:考虑斜拉索的垂度效应。
工况3:考虑垂度效应+梁柱效应。
工况4:考虑垂度效应+梁柱效应+大位移效应。
4.2 主梁弯矩计算结果
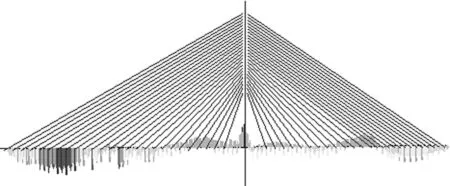
图4 线性分析主梁弯矩示意图
图4为该桥线性分析下的成桥状态主梁弯矩分布图,主梁正弯矩峰值出现在主跨跨中截面,负弯矩峰值出现在在塔梁结合处,主边跨的最大弯矩值为负弯矩,出现在辅助墩处,副边跨的最大弯矩为正弯矩,出现在该跨跨中截面。据此,选取主跨跨中截面作为控制截面A,选取塔梁结合处作为控制截面B,与辅助墩结合处的主梁截面作为控制截面C,次边跨跨中截面作为控制截面D,控制截面见图5。
分别计算4种工况下主梁控制截面的弯矩值以及工况2、工况3、工况4分别相对于工况1的弯矩增量百分比,计算结果见表2。
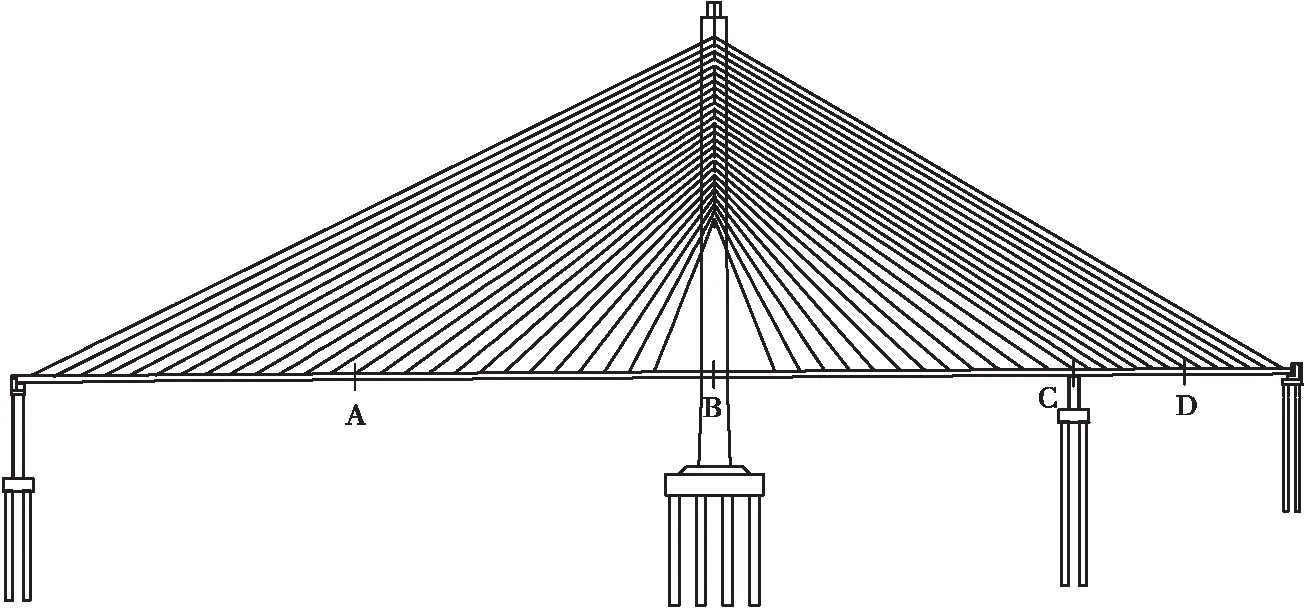
图5 控制截面示意图

表2 4种工况下主梁控制截面弯矩值及增量比控制截面工况1弯矩值/(kN·m)工况2弯矩值/(kN·m)增量比/%工况3弯矩值/(kN·m)增量比/%工况4弯矩值/(kN·m)增量比/%A59 991.50 62 100.32 3.5262 484.22 4.1666 567.87 10.96B-33 221.07 -34 022.40 2.41-37 107.55 11.70-40 340.23 21.43C-28 772.01 -29 146.02 1.30-29 206.49 1.51-30 115.51 4.67D36 025.36 36 579.86 1.5436 867.40 2.3438 638.98 7.25
由表2可知,在成桥状态下,4个主梁控制截面的弯矩值从工况1到工况4依次增加,由此可看出,考虑垂度效应、梁柱效应与大位移效应均会导致主梁弯矩有不同程度的增大。
对比工况1与工况2可知,该桥的主跨跨中截面弯矩增量比最大,为3.52%,说明垂度效应对该截面弯矩影响最大,分析其原因为换算弹性模量后斜拉索的弹性模量减小,对主梁竖向支撑能力减弱,主梁挠度增大,而该截面由于竖向约束最弱(拉索竖向分力小且无桥墩支撑),挠度也达到最大,进而导致弯矩最大增量出现在该截面。
对比工况2与工况3可知,梁柱效应对塔梁固结处的弯矩影响最大,对其他几个控制截面弯矩影响较小。只考虑梁柱效应时的弯矩增量比仅为2.41%,考虑垂度效应和梁柱效应后,主梁弯矩的增量比达到了11.70%。考虑为边界设置的原因。相较于其他几个截面,由于该处为塔梁固结,该截面在主梁变形过程中受到的约束最大,导致内力响应剧烈,弯矩与轴力的耦合效应达到峰值。
对比工况3与工况4,主梁各控制截面弯矩均有明显增长,尤其在塔梁固结处,增量比由11.70%增长到了21.43%,说明大位移效应对该桥主梁弯矩的影响最大。分析其原因为:该独塔斜拉桥主梁下挠使主梁所受荷载的作用位置和方向发生了显著变化,结构的几何刚度矩阵降低,因此主梁内力显著增加。
5 结论
以某大跨径独塔斜拉桥为例,采用MIDAS/CIVIL建立该桥空间有限元模型,对比分析了该桥考虑垂度效应、梁柱效应与大位移效应时主梁的内力响应特点,可得到以下结论:
1) 考虑垂度效应、梁柱效应与大位移效应均会导致主梁弯矩有不同程度增大,因此,独塔斜拉桥考虑非线性影响的计算结果更偏安全。
2) 大位移效应和梁柱效应是该桥主梁弯矩增大的主要因素,垂度效应对该桥主梁弯矩影响相对较小。
3) 独塔斜拉桥在成桥状态下,主梁在主跨跨中与塔梁结合处对于几何非线性因素影响最敏感,在边跨辅助墩与次边跨跨中处敏感性较弱。

